|
L'Hopital's rule |
|
L'Hopital's rule is a method for calculating limits that have uncertainty of type or . Let a is some finite real number or equal to infinity. L'Hopital's rule can also be applied to uncertainties such as
L'Hopital's rule is also valid for one-sided limits. |
|
Example 1 |
|
Calculate the limit. Solution. Differentiating the numerator and denominator, we find the value of the limit: |
|
Example 2 |
|
Calculate the limit. Solution. Since direct substitution leads to uncertainty of type , we apply L'Hopital's rule. |
|
Example 3 |
|
Calculate limit Solution. Here we are dealing with type uncertainty. After simple transformations, we get |
|
Example 4 |
|
Find the limit. Solution. Using L'Hopital's rule, we can write
|
|
Example 5 |
|
Find the limit. Solution. Here we encounter type uncertainty. Let's denote . After logarithm we get Respectively, |
|
Example 6 |
15. L'Hopital's rules*
Swiss mathematician Johann I Bernoulli(1667-1748) after successfully graduating from the University of Basel, traveling around Europe, he came to Paris in 1690. In the literary salon of the philosopher Nicolas Malebranche (1638-1715), Johann met the French mathematician Marquis Guillaume François Antoine de L'Hôpital (1661-1704). During a lively conversation, L'Hopital was surprised at how easily, “as if playing,” the young Bernoulli solved difficult problems in the new calculus. Therefore, L'Hopital asked to give him several lectures. L'Hopital liked the oral conversations, and he began to receive written materials for a decent fee. Note that the now well-known “L'Hopital rule” for disclosing uncertainties was also conveyed to him by Johann. Already in 1696, L'Hopital's famous treatise “Introduction to the Analysis of Infinitesimals for the Understanding of Curved Lines” appeared. The second part of the course, presented by Johann I Bernoulli, was published only in 1742 and was called “Mathematical lectures on the method of integrals and others; written for the famous Marquis of Hospital; years 1691-1692.” In 1921, handwritten copies of lectures were discovered in the handwriting of Johann I Bernoulli, the originals of which were transferred to the L'Hopital in 1691-1692. Of these, scientists unexpectedly discovered that Loptal in his “Analysis” almost did not deviate from the lectures of his young teacher.
Theorem (Cauchy). Let the functions and be continuous on and differentiable on and . Then :
![]()
Proof. Consider the function
Let us choose so that all the conditions of Rolle’s theorem are satisfied, i.e. .

According to Rolle's theorem, there is:
L'Hopital's first rule
Definition. Let the functions , continuous on , be differentiable at , and let . Let . Then we say that the relation at represents an uncertainty of the form .
Theorem.
![]()
![]()
Let us apply Cauchy's theorem to the segment where . Exists :
![]()
and, therefore,
![]()
This means that ![]() .
.
In the case when it is infinite, inequality (1) is replaced by
depending on the sign. The rest of the proof remains unchanged.
L'Hopital's second rule
Definition. Let the functions , be continuous and differentiable in , and . Let . Then we say that the relation at represents an uncertainty of the form .
Theorem. If, under the specified conditions, there is
![]()
![]()
Proof. Let it be of course. By choosing: the inequality holds in the interval
Let's define the function from the condition
![]()
at . Let us apply Cauchy's theorem to the segment. We get that there is:
For those for whom
Since it is arbitrarily small, then
![]()
In the case when , inequality (2) is replaced by
and inequality (4) – to the inequality
![]()
taking place at , sufficiently close to a due to (3).
The case is treated similarly.
Solution online function limits. Find the limiting value of a function or functional sequence at a point, calculate ultimate the value of the function at infinity. determining the convergence of a number series and much more can be done thanks to our online service -. We allow you to find function limits online quickly and accurately. You enter it yourself function variable and the limit to which it strives, our service carries out all the calculations for you, giving an accurate and simple answer. And for finding the limit online you can enter both numerical series and analytical functions containing constants in literal expression. In this case, the found limit of the function will contain these constants as constant arguments in the expression. Our service solves any complex tasks by finding limits online, it is enough to indicate the function and the point at which it is necessary to calculate limit value of function. Calculating online limits, you can use various methods and rules for solving them, while checking the result obtained with solving limits online on the www.site, which will lead to the successful completion of the task - you will avoid your own mistakes and clerical errors. Or you can completely trust us and use our result in your work, without spending extra effort and time on independently calculating the limit of the function. We allow input of limit values such as infinity. You must enter a common term number sequence And www.site will calculate the value limit online to plus or minus infinity.
One of the main concepts mathematical analysis is function limit And sequence limit at a point and at infinity, it is important to be able to solve correctly limits. With our service this will not be difficult. A decision is made limits online within a few seconds, the answer is accurate and complete. The study of mathematical analysis begins with transition to the limit, limits are used in almost all areas of higher mathematics, so it is useful to have a server at hand for online limit solutions, which is matematikam.ru.
Imagine a flock of sparrows with bulging eyes. No, this is not thunder, not a hurricane, or even a little boy with a slingshot in his hands. It’s just that a huge, huge cannonball is flying into the very thick of the chicks. That's right L'Hopital's rules deal with the limits within which uncertainty or .
L'Hôpital's rules are a very powerful method that allows you to quickly and effectively eliminate these uncertainties, it is no coincidence that in collections of problems, on tests, in tests there is often a persistent stamp: “calculate the limit, without using L'Hopital's rule" The requirement highlighted in bold can be applied with a clear conscience to any lesson limit Limits. Examples of solutions, Wonderful Limits. Methods for solving limits, Remarkable equivalences, where the uncertainty “zero to zero” or “infinity to infinity” occurs. Even if the task is formulated briefly - “calculate the limits”, it is tacitly understood that you will use everything, but not the rules of L'Hopital.
There are two rules in total, and they are very similar to each other, both in essence and in the method of application. In addition to direct examples on the topic, we will also study additional material, which will be useful in further study of mathematical analysis.
I’ll make a reservation right away that the rules will be presented in a laconic “practical” form, and if you have to take the theory test, I recommend turning to the textbook for more rigorous calculations.
L'Hopital's first rule
Let's consider the functions that infinitesimal at some point. If there is a limit to their relationship, then in order to eliminate uncertainty we can take two derivatives- from the numerator and from the denominator. In this case: ![]() , that is .
, that is .
Note : The limit must also exist, otherwise the rule does not apply.
What follows from the above?
Firstly, you need to be able to find derivatives of functions, and the better the better =)
Secondly, derivatives are taken SEPARATELY from the numerator and SEPARATELY from the denominator. Please do not confuse with the rule of differentiation of quotients  !!!
!!!
And thirdly, “X” can tend anywhere, including to infinity - as long as there is uncertainty.
Let's return to Example 5 of the first article about the limits, which produced the following result: ![]()
For uncertainty 0:0 we apply L'Hôpital's first rule:
As you can see, differentiation of the numerator and denominator led us to the answer in half a turn: we found two simple derivatives, substituted the “two” in them, and it turned out that the uncertainty disappeared without a trace!
It is not uncommon for L'Hôpital's rules to be applied two or more times in succession (this also applies to the second rule). Let's take it out for a retro evening Lesson Example 2 about wonderful limits:
Two bagels are again cooling on the bunk bed. Let's apply L'Hopital's rule: 
Please note that in the first step the denominator is taken derivative of a complex function. After this, we carry out a number of intermediate simplifications, in particular, we get rid of the cosine, indicating that it tends to unity. The uncertainty is not eliminated, so we apply L'Hopital's rule again (second line).
I deliberately chose a not the simplest example so that you can do a little self-test. If it is not entirely clear how they were found derivatives, you should strengthen your differentiation technique, if the cosine trick is not clear, please go back to remarkable limits. I don’t see much point in step-by-step comments, since I have already talked about derivatives and limits in sufficient detail. The novelty of the article lies in the rules themselves and some technical solutions.
As already noted, in most cases L'Hopital's rules do not need to be used, but they are often advisable to use for a rough check of a solution. Often, but not always. So, for example, it is much more profitable to check the example just considered through wonderful equivalences.
L'Hopital's second rule
Brother-2 fights two sleeping eights. Likewise:
If there is a relation limit infinitely large at the function point: , then in order to eliminate uncertainty we can take two derivatives– SEPARATELY from the numerator and SEPARATELY from the denominator. In this case: ![]() , that is when differentiating the numerator and denominator, the value of the limit does not change.
, that is when differentiating the numerator and denominator, the value of the limit does not change.
Note : there must be a limit
Again, in different practical examples the meaning may be different, including infinite. It is important that there is uncertainty.
Let's check Example No. 3 of the first lesson: ![]() . We use L'Hopital's second rule:
. We use L'Hopital's second rule:
Since we're talking about giants, let's look at two canonical limits:
Example 1
Calculate limit
It is not easy to get an answer using “conventional” methods, so to reveal the uncertainty “infinity to infinity” we use L'Hopital's rule: 
Thus, linear function higher order of growth than a logarithm with a base greater than one(etc.). Of course, “X’s” in higher powers will also “pull” such logarithms. Indeed, the function grows quite slowly and its schedule is flatter relative to the same “X”.
Example 2
Calculate limit
Another familiar shot. In order to eliminate uncertainty, we use L'Hopital's rule, moreover, twice in a row:
Exponential function, with a base greater than one(etc.) higher order of growth than power function with a positive degree.
Similar limits are encountered during full function study, namely, when finding asymptotes of graphs. They are also noticeable in some tasks probability theory. I advise you to take note of the two examples discussed; this is one of the few cases when there is nothing better than differentiating the numerator and denominator.
Further in the text I will not distinguish between the first and second rules of L'Hôpital; this was done only for the purpose of structuring the article. In general, from my point of view, it is somewhat harmful to over-number mathematical axioms, theorems, rules, properties, since phrases like “according to Corollary 3 of Theorem 19...” are informative only within the framework of a particular textbook. In another source of information the same thing will be “Corollary 2 and Theorem 3”. Such statements are formal and convenient only for the authors themselves. Ideally, it is better to refer to the essence of the mathematical fact. The exception is historically established terms, for example, first wonderful limit or second wonderful limit.
We continue to develop a topic that was suggested to us by a member of the Paris Academy of Sciences, Marquis Guillaume Francois de L'Hopital. The article takes on a pronounced practical flavor and in a fairly common task it is required:
To warm up, let's deal with a couple of small sparrows:
Example 3
The limit can be first simplified by getting rid of the cosine, but let’s show respect for the condition and immediately differentiate the numerator and denominator: 
There is nothing non-standard in the process of finding derivatives; for example, the denominator uses the usual differentiation rule works ![]() .
.
The considered example is resolved through wonderful limits, a similar case is discussed at the end of the article Complex Limits.
Example 4
Calculate the limit using L'Hopital's rule ![]()
This is an example for independent decision. Good joke =)
A typical situation is when, after differentiation, three- or four-story fractions are obtained:
Example 5
Calculate the limit using L'Hopital's rule
Begs to be used remarkable equivalence, but the path is strictly predetermined by the condition:
After differentiation, I strongly recommend getting rid of the multi-story fraction and carrying out maximum simplifications. Of course, more prepared students may skip last step and immediately write down:  , but even excellent students will get confused within certain limits.
, but even excellent students will get confused within certain limits.
Example 6
Calculate the limit using L'Hopital's rule
Example 7
Calculate the limit using L'Hopital's rule
These are examples for you to decide on your own. In Example 7, you don’t have to simplify anything; the fraction obtained after differentiation is too simple. But in Example 8, after applying L'Hopital's rule, it is highly desirable to get rid of the three-story structure, since the calculations will not be the most convenient. Full solution and answer at the end of the lesson. If you have any difficulties - trigonometric table to help.
And, simplifications are absolutely necessary when, after differentiation, uncertainty not resolved.
Example 8
Calculate the limit using L'Hopital's rule
Let's go: 
It is interesting that the original uncertainty after the first differentiation turned into uncertainty, and L'Hôpital's rule is calmly applied further. Also notice how after each “approach” the four-story fraction is eliminated, and the constants are moved beyond the limit sign. In simpler examples, it is more convenient not to include constants, but when the limit is complex, we simplify everything, everything, everything. The insidiousness of the solved example also lies in the fact that when ![]() , and , therefore, during the elimination of sines, it is not surprising to get confused in the signs. In the penultimate line, the sines could not have been killed, but the example is quite heavy, forgivable.
, and , therefore, during the elimination of sines, it is not surprising to get confused in the signs. In the penultimate line, the sines could not have been killed, but the example is quite heavy, forgivable.
The other day I came across an interesting task:
Example 9
To be honest, I doubted a little what this limit would be equal to. As demonstrated above, "x" is more high order height than the logarithm, but will it “outweigh” the cubed logarithm? Try to find out for yourself who will win.
Yes, L'Hopital's rules are not only about shooting sparrows with a cannon, but also painstaking work...
In order to apply L'Hopital's rules to bagels or tired eights, uncertainties of the form are reduced.
Dealing with uncertainty is discussed in detail in Examples No. 9-13 of the lesson. Methods for solving limits. Let's take another one for the record:
Example 10
Calculate the limit of a function using L'Hopital's rule ![]()
At the first step, we bring the expression to a common denominator, thereby transforming uncertainty into uncertainty. And then we charge L'Hopital's rule: 
Here, by the way, is the case when touching the four-story expression is pointless.
Uncertainty also does not resist turning into or:
Example 11
Calculate the limit of a function using L'Hopital's rule
The limit here is one-sided, and such limits have already been discussed in the manual Graphs and properties of functions. As you remember, the graph of the “classical” logarithm does not exist to the left of the axis, so we can only approach zero from the right.
L'Hopital's rules for one-sided limits work, but uncertainty must first be dealt with. At the first step, we make a three-story fraction, obtaining uncertainty, then the solution follows a template scheme: 
After differentiating the numerator and denominator, we get rid of the four-story fraction to carry out simplifications. As a result, uncertainty emerged. We repeat the trick: we again make the fraction three-story and apply L'Hopital's rule to the resulting uncertainty again:
Ready.
One could try to reduce the original limit to two donuts: 
But, firstly, the derivative in the denominator is more difficult, and secondly, nothing good will come of this.
Thus, Before solving similar examples, you need to analyze(orally or in a draft), WHICH uncertainty is more advantageous to reduce to - to “zero to zero” or to “infinity to infinity”.
In turn, drinking buddies and more exotic comrades join the fire. The transformation method is simple and standard.
- L'Hopital's rule and the disclosure of uncertainties
- Disclosure of uncertainties of the types “zero divided by zero” and “infinity divided by infinity”
- Uncovering uncertainties of the form “zero times infinity”
- Disclosure of uncertainties of the types "zero to the power of zero", "infinity to the power of zero" and "one to the power of infinity"
- Disclosure of uncertainties of the form "infinity minus infinity"
L'Hopital's rule and the disclosure of uncertainties
Disclosure of uncertainties of the form 0/0 or ∞/∞ and some other uncertainties is greatly simplified using L'Hopital's rule.
The essence L'Hopital's rules is that in the case when calculating the limit of the ratio of two functions gives uncertainties of the form 0/0 or ∞/∞, the limit of the ratio of the two functions can be replaced by the limit of the ratio of their derivatives and, thus, obtain a certain result.
In general, L'Hopital's rules mean several theorems that can be expressed in the following single formulation.
L'Hopital's rule. If the functions f(x) And g(x) are differentiable in a certain neighborhood of the point , with the possible exception of the point itself, and in this neighborhood
![]()
![]()
![]() (1)
(1)
In other words, for uncertainties of the form 0/0 or ∞/∞, the limit of the ratio of two functions is equal to the limit of the ratio of their derivatives, if the latter exists (finite or infinite).
In equality (1), the value to which the variable tends can be either a finite number, or infinity, or minus infinity.
Uncertainties of other types can also be reduced to uncertainties of the types 0/0 and ∞/∞.
Disclosure of uncertainties of the types “zero divided by zero” and “infinity divided by infinity”
Example 1. Calculate
![]()
x=2 leads to uncertainty of the form 0/0. Therefore, we apply L'Hopital's rule:

Example 2. Calculate
Solution. Substitution in given function values x

Example 3. Calculate
Solution. Substituting a value into a given function x=0 leads to uncertainty of the form 0/0. Therefore, we apply L'Hopital's rule:

Example 4. Calculate
Solution. Substituting the value x equal to plus infinity into a given function leads to an uncertainty of the form ∞/∞. Therefore, we apply L'Hopital's rule:
Comment. If the limit of the derivative ratio is an uncertainty of the form 0/0 or ∞/∞, then L'Hopital's rule can be applied again, i.e. go to the limit of the ratio of second derivatives, etc.
Example 5. Calculate
Solution. We find

Here L'Hopital's rule is applied twice, since both the limit of the ratio of functions and the limit of the ratio of derivatives give an uncertainty of the form ∞/∞.
Example 6. Calculate

We have already begun to understand the limits and their solution. Let's continue in hot pursuit and figure out how to solve the limits according to L'Hopital's rule. This simple rule able to help you get out of the insidious and complex traps that teachers love to use in examples on tests in higher mathematics and calculus. The solution using L'Hopital's rule is simple and quick. The main thing is to be able to differentiate.
L'Hopital's Rule: History and Definition
In fact, this is not exactly L'Hopital's rule, but a rule L'Hopital-Bernoulli. It was formulated by a Swiss mathematician Johann Bernoulli, and the Frenchman Guillaume L'Hopital first published in his textbook infinitesimals in the glorious 1696 year. Can you imagine how people had to solve the limits with the revelation of uncertainties before this happened? We are not.

Before starting to analyze L'Hopital's rule, we recommend reading the introductory article about and methods for solving them. Often in tasks there is a formulation: find the limit without using L'Hopital's rule. Read about the techniques that will help you with this in our article.
If you are dealing with fraction limits of two functions, be prepared: you will soon encounter uncertainty of the form 0/0 or infinity/infinity. How to understand this? The numerator and denominator of the expression tend to zero or infinity. What to do with such a limit is, at first glance, completely unclear. However, if you apply L'Hopital's rule and think a little, everything falls into place.
But let us formulate the L'Hopital-Bernoulli rule. To be absolutely precise, it is expressed by a theorem. L'Hopital's rule, definition:
If two functions are differentiable in a neighborhood of a point x=a vanish at this point, and there is a limit on the ratio of the derivatives of these functions, then when X striving for A there is a limit on the ratio of the functions themselves, equal to the limit on the ratio of the derivatives.
Let's write down the formula, and everything will immediately become simpler. L'Hopital's rule, formula:

Since we are interested in the practical side of the issue, we will not give the proof of this theorem here. You will either have to take our word for it, or find it in any textbook on mathematical analysis and make sure that the theorem is true.
By the way! For our readers there is now a 10% discount on
Uncertainty disclosure using L'Hopital's rule
What uncertainties can L'Hopital's rule help resolve? Previously we talked mainly about uncertainty 0/0 . However, this is far from the only uncertainty that can be encountered. Here are other types of uncertainties:

Let's consider transformations that can be used to reduce these uncertainties to the form 0/0 or infinity/infinity. After the transformation, you can apply the L'Hopital-Bernoulli rule and click examples like nuts.

Species uncertainty infinity/infinity comes down to uncertainty of the form 0/0 simple transformation:

Let there be a product of two functions, one of which the first tends to zero, and the second - to infinity. We apply a transformation, and the product of zero and infinity turns into uncertainty 0/0 :

To find limits with uncertainties like infinity minus infinity we use the following transformation leading to uncertainty 0/0 :

In order to use L'Hopital's rule, you need to be able to take derivatives. Below is a table of derivatives of elementary functions, which you can use when solving examples, as well as rules for calculating derivatives of complex functions:

Now let's move on to examples.
Example 1
Find the limit using L'Hopital's rule:

Example 2
Calculate using L'Hopital's rule:

Important point! If the limit of the second and subsequent derivative functions exists at X striving for A , then L'Hopital's rule can be applied several times.
Let's find the limit ( n – natural number). To do this, we apply L'Hopital's rule n once:

We wish you good luck in mastering mathematical analysis. And if you need to find the limit using L'Hopital's rule, write an essay using L'Hopital's rule, calculate the roots differential equation or even calculate the inertia tensor of a body, contact our authors. They will be happy to help you understand the intricacies of the solution.
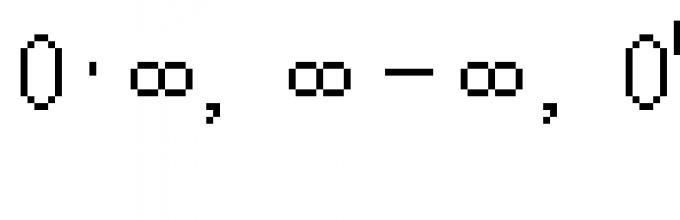
 .
.







