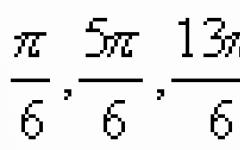Answer:
Projection properties:
Vector Projection Properties
Property 1.
The projection of the sum of two vectors onto an axis is equal to the sum of the projections of vectors onto the same axis: 
This property allows you to replace the projection of a sum of vectors with the sum of their projections and vice versa.
Property 2. If a vector is multiplied by the number λ, then its projection onto the axis is also multiplied by this number:
Property 3.
The projection of the vector onto the l axis is equal to the product of the vector modulus and the cosine of the angle between the vector and the axis:
Orth axis. Decomposition of a vector in coordinate unit vectors. Vector coordinates. Coordinate Properties
Answer:
Unit vectors of the axes.
A rectangular coordinate system (of any dimension) is also described by a set of unit vectors aligned with the coordinate axes. The number of unit vectors is equal to the dimension of the coordinate system and they are all perpendicular to each other.
In the three-dimensional case, the unit vectors are usually denoted
And Arrow symbols and may also be used.
In this case, in the case of a right coordinate system, the following formulas with vector products of unit vectors are valid:
Decomposition of a vector in coordinate unit vectors.
The unit vector of the coordinate axis is denoted by , axes by , axes by (Fig. 1)
For any vector that lies in the plane, the following expansion takes place:
If the vector 
located in space, then the expansion in unit vectors of the coordinate axes has the form:
Vector coordinates:
To calculate the coordinates of a vector, knowing the coordinates (x1; y1) of its beginning A and the coordinates (x2; y2) of its end B, you need to subtract the coordinates of the beginning from the coordinates of the end: (x2 – x1; y2 – y1).
Properties of coordinates.
Consider a coordinate line with the origin at point O and the unit vector i. Then for any vector a on this line: a = axi.
The number ax is called the coordinate of the vector a on the coordinate axis.
Property 1. When adding vectors on an axis, their coordinates are added.
Property 2. When a vector is multiplied by a number, its coordinate is multiplied by that number.
Dot product vectors. Properties.
Answer:
The scalar product of two non-zero vectors is the number
equal to the product of these vectors and the cosine of the angle between them.
Properties:
1. The scalar product has the commutative property: ab=ba
Scalar product of coordinate unit vectors. Determination of the scalar product of vectors specified by their coordinates.
Answer:
Dot product (×) of unit vectors
| (X) | I | J | K |
| I | |||
| J | |||
| K |
Determination of the scalar product of vectors specified by their coordinates.
The scalar product of two vectors and given by their coordinates can be calculated using the formula
The cross product of two vectors. Properties vector product.
Answer:
Three non-coplanar vectors form a right-handed triple if, from the end of the third, the rotation from the first vector to the second is made counterclockwise. If clockwise, then left. If not, then in the opposite direction ( show how he showed with “handles”)
Cross product of a vector A to vector b called a vector from which:
1. Perpendicular to vectors A And b
2. Has length, numerically equal to the area parallelogram formed on a And b vectors
3. Vectors, a ,b, And c form a right-hand triple of vectors
Properties:
1. 
3. 
4. 
Vector product of coordinate unit vectors. Determination of the vector product of vectors specified by their coordinates.
Answer:
Vector product of coordinate unit vectors.
Determination of the vector product of vectors specified by their coordinates.
Let the vectors a = (x1; y1; z1) and b = (x2; y2; z2) be given by their coordinates in the rectangular Cartesian coordinate system O, i, j, k, and the triple i, j, k is right-handed.
Let's expand a and b into basis vectors:
a = x 1 i + y 1 j + z 1 k, b = x 2 i + y 2 j + z 2 k.
Using the properties of the vector product, we get
[A; b] = =
= x 1 x 2 + x 1 y 2 + x 1 z 2 +
+ y 1 x 2 + y 1 y 2 + y 1 z 2 +
+ z 1 x 2 + z 1 y 2 + z 1 z 2 . (1)
By the definition of a vector product we find
= 0, = k, = - j,
= - k, = 0, = i,
= j, = - i. = 0.
Taking these equalities into account, formula (1) can be written as follows:
[A; b] = x 1 y 2 k - x 1 z 2 j - y 1 x 2 k + y 1 z 2 i + z 1 x 2 j - z 1 y 2 i
[A; b] = (y 1 z 2 - z 1 y 2) i + (z 1 x 2 - x 1 z 2) j + (x 1 y 2 - y 1 x 2) k. (2)
Formula (2) gives an expression for the vector product of two vectors specified by their coordinates.
The resulting formula is cumbersome. Using the notation of determinants, you can write it in another form that is more convenient for memorization:
Usually formula (3) is written even shorter:
In physics for grade 9 (I.K.Kikoin, A.K.Kikoin, 1999),
task №5
to the chapter " CHAPTER 1. GENERAL INFORMATION ABOUT TRAFFIC».
1. What is called the projection of a vector onto the coordinate axis?
1. The projection of vector a onto the coordinate axis is the length of the segment between the projections of the beginning and end of vector a (perpendiculars dropped from these points onto the axis) onto this coordinate axis.
2. How is the displacement vector of a body related to its coordinates?
2. Projections of the displacement vector s onto coordinate axes equal to the change in the corresponding body coordinates.
3. If the coordinate of a point increases over time, then what sign does the projection of the displacement vector onto the coordinate axis have? What if it decreases?
3. If the coordinate of a point increases over time, then the projection of the displacement vector onto the coordinate axis will be positive, because in this case we will go from the projection of the beginning to the projection of the end of the vector in the direction of the axis itself.
If the coordinate of a point decreases over time, then the projection of the displacement vector onto the coordinate axis will be negative, because in this case we will go from the projection of the beginning to the projection of the end of the vector against the guide of the axis itself.
4. If the displacement vector is parallel to the X axis, then what is the modulus of the projection of the vector onto this axis? And what about the modulus of the projection of the same vector onto the Y axis?
4. If the displacement vector is parallel to the X axis, then the modulus of the vector’s projection onto this axis is equal to the modulus of the vector itself, and its projection onto the Y axis is zero.
5. Determine the signs of the projections onto the X axis of the displacement vectors shown in Figure 22. How do the coordinates of the body change during these displacements?
5. In all the following cases, the Y coordinate of the body does not change, and the X coordinate of the body will change as follows:
a) s 1;
the projection of the vector s 1 onto the X axis is negative and is equal in absolute value to the length of the vector s 1 . With such a movement, the X coordinate of the body will decrease by the length of the vector s 1.
b) s 2 ;
the projection of the vector s 2 onto the X axis is positive and equal in magnitude to the length of the vector s 1 . With such a movement, the X coordinate of the body will increase by the length of the vector s 2.
c) s 3 ;
the projection of the vector s 3 onto the X axis is negative and equal in magnitude to the length of the vector s 3 . With such a movement, the X coordinate of the body will decrease by the length of the vector s 3.
d)s 4;
the projection of the vector s 4 onto the X axis is positive and equal in magnitude to the length of the vector s 4 . With such a movement, the X coordinate of the body will increase by the length of the vector s 4.
e)s 5;
the projection of the vector s 5 on the X axis is negative and equal in magnitude to the length of the vector s 5 . With such a movement, the X coordinate of the body will decrease by the length of the vector s 5.
6. If the distance traveled is large, then can the displacement module be small?
6. Maybe. This is because the displacement (displacement vector) is vector quantity, i.e. is a directed straight line segment connecting the initial position of the body with its subsequent positions. And the final position of the body (regardless of the distance traveled) can be as close as desired to the initial position of the body. If the final and initial positions of the body coincide, the displacement module will be equal to zero.
7. Why is the vector of movement of a body more important in mechanics than the path it has traveled?
7. The main task of mechanics is to determine the position of the body at any time. Knowing the vector of movement of the body, we can determine the coordinates of the body, i.e. the position of the body at any moment in time, and knowing only the distance traveled, we cannot determine the coordinates of the body, because we have no information about the direction of movement, but can only judge the length of the distance traveled at the moment time.
§ 3. Projections of a vector on the coordinate axes1. Finding projections geometrically.
Vector
- projection of the vector onto the axis OX
- projection of the vector onto the axis OY
Definition 1. Vector projection on any coordinate axis is a number taken with a plus or minus sign, corresponding length of the segment, located between the bases of the perpendiculars dropped from the beginning and end of the vector to the coordinate axis.
The projection sign is defined as follows. If, when moving along the coordinate axis, there is a movement from the projection point of the beginning of the vector to the projection point of the end of the vector in the positive direction of the axis, then the projection of the vector is considered positive. If it is opposite to the axis, then the projection is considered negative.
The figure shows that if the vector is oriented somehow opposite to the coordinate axis, then its projection onto this axis is negative. If a vector is oriented somehow in the positive direction of the coordinate axis, then its projection onto this axis is positive.
If a vector is perpendicular to the coordinate axis, then its projection onto this axis is zero.
If a vector is codirectional with an axis, then its projection onto this axis is equal to the absolute value of the vector.
If a vector is directed oppositely to the coordinate axis, then its projection onto this axis is equal in absolute value to the absolute value of the vector taken with a minus sign.
2. Most general definition projections.
From a right triangle ABD:.
Definition 2. Vector projection on any coordinate axis is a number equal to the product of the modulus of the vector and the cosine of the angle formed by the vector with the positive direction of the coordinate axis.
The sign of the projection is determined by the sign of the cosine of the angle formed by the vector with the positive axis direction.
If the angle is acute, then the cosine has a positive sign and the projections are positive. For obtuse angles, the cosine has a negative sign, so in such cases the projections onto the axis are negative. 
- therefore, for vectors perpendicular to the axis, the projection is zero.
Let two vectors and be given in space. Let's postpone from an arbitrary point O vectors and . Angle between vectors is called the smallest of the angles. Designated 
.
Consider the axis l and plot a unit vector on it (i.e., a vector whose length is equal to one).
At an angle between the vector and the axis l understand the angle between the vectors and .
So let l is some axis and is a vector.
Let us denote by A 1 And B 1 projections onto the axis l respectively points A And B. Let's assume that A 1 has a coordinate x 1, A B 1– coordinate x 2 on the axis l.
Then projection vector per axis l called difference x 1 – x 2 between the coordinates of the projections of the end and beginning of the vector onto this axis.
Projection of the vector onto the axis l we will denote .
It is clear that if the angle between the vector and the axis l spicy then x 2> x 1, and projection x 2 – x 1> 0; if this angle is obtuse, then x 2< x 1 and projection x 2 – x 1< 0. Наконец, если вектор перпендикулярен оси l, That x 2= x 1 And x 2– x 1=0.
Thus, the projection of the vector onto the axis l is the length of the segment A 1 B 1, taken with a certain sign. Therefore, the projection of the vector onto the axis is a number or a scalar.
The projection of one vector onto another is determined similarly. In this case, the projections of the ends of this vector onto the line on which the 2nd vector lies are found.
Let's look at some basic properties of projections.
LINEARLY DEPENDENT AND LINEARLY INDEPENDENT VECTOR SYSTEMS
Let's consider several vectors.
Linear combination of these vectors is any vector of the form , where are some numbers. The numbers are called linear combination coefficients. They also say that in this case it is linearly expressed through these vectors, i.e. is obtained from them using linear actions.
For example, if three vectors are given, then the following vectors can be considered as their linear combination: 
If a vector is represented as a linear combination of some vectors, then it is said to be laid out along these vectors.
The vectors are called linearly dependent, if there are numbers, not all equal to zero, such that 
. It is clear that given vectors will be linearly dependent if any of these vectors is linearly expressed through the others.
Otherwise, i.e. when the ratio performed only when 
, these vectors are called linearly independent.
Theorem 1. Any two vectors are linearly dependent if and only if they are collinear.
Proof:
The following theorem can be proven similarly.
Theorem 2. Three vectors are linearly dependent if and only if they are coplanar.
Proof.
BASIS
Basis is the collection of non-zeros linearly independent vectors. We will denote the elements of the basis by .
In the previous paragraph, we saw that two non-collinear vectors on a plane are linearly independent. Therefore, according to Theorem 1 from the previous paragraph, a basis on a plane is any two non-collinear vectors on this plane.
Similarly, any three non-coplanar vectors are linearly independent in space. Consequently, we call three non-coplanar vectors a basis in space.
The following statement is true.
Theorem. Let a basis be given in space. Then any vector can be represented as a linear combination 
, Where x, y, z- some numbers. This is the only decomposition.
Proof.
Thus, the basis allows each vector to be uniquely associated with a triple of numbers - the coefficients of the expansion of this vector into the basis vectors: . The converse is also true, for every three numbers x, y, z using the basis, you can compare the vector if you make a linear combination 
.
If the basis and , then the numbers x, y, z are called coordinates vector in a given basis. Vector coordinates are denoted by .
CARTESIAN COORDINATE SYSTEM
Let a point be given in space O and three non-coplanar vectors.
Cartesian coordinate system in space (on the plane) is the collection of a point and a basis, i.e. a set of a point and three non-coplanar vectors (2 non-collinear vectors) emanating from this point.
Dot O called the origin; straight lines passing through the origin of coordinates in the direction of the basis vectors are called coordinate axes - the abscissa, ordinate and applicate axis. Planes passing through the coordinate axes are called coordinate planes.
Consider an arbitrary point in the selected coordinate system M. Let us introduce the concept of point coordinates M. Vector connecting the origin to a point M. called radius vector points M.
A vector in the selected basis can be associated with a triple of numbers – its coordinates: 
.
Coordinates of the radius vector of the point M. are called coordinates of point M. in the coordinate system under consideration. M(x,y,z). The first coordinate is called the abscissa, the second is the ordinate, and the third is the applicate.
Cartesian coordinates on the plane are determined similarly. Here the point has only two coordinates - abscissa and ordinate.
It is easy to see that for a given coordinate system, each point has certain coordinates. On the other hand, for each triple of numbers there is a unique point that has these numbers as coordinates.
If the vectors taken as a basis in the selected coordinate system have unit length and are pairwise perpendicular, then the coordinate system is called Cartesian rectangular.
It is easy to show that .
The direction cosines of a vector completely determine its direction, but say nothing about its length.
A vector description of movement is useful, since in one drawing you can always depict many different vectors and get a visual “picture” of movement before your eyes. However, using a ruler and a protractor every time to perform operations with vectors is very labor-intensive. Therefore, these actions reduce to actions with positive and negative numbers– projections of vectors.
Projection of the vector onto the axis called a scalar quantity equal to the product of the modulus of the projected vector and the cosine of the angle between the directions of the vector and the selected coordinate axis.
The left drawing shows a displacement vector, the module of which is 50 km, and its direction forms obtuse angle 150° with the direction of the X axis. Using the definition, we find the projection of the displacement on the X axis:
sx = s cos(α) = 50 km cos(150°) = –43 km
Since the angle between the axes is 90°, it is easy to calculate that the direction of movement forms with the direction of the Y axis acute angle 60°. Using the definition, we find the projection of displacement on the Y axis:
sy = s cos(β) = 50 km cos(60°) = +25 km
As you can see, if the direction of the vector forms an acute angle with the direction of the axis, the projection is positive; if the direction of the vector forms an obtuse angle with the direction of the axis, the projection is negative.
The right drawing shows a velocity vector, the module of which is 5 m/s, and the direction forms an angle of 30° with the direction of the X axis. Let's find the projections:
υx = υ cos(α) = 5 m/s cos( 30°) = +4.3 m/s
υy = υ · cos(β) = 5 m/s · cos( 120°) = –2.5 m/s
It is much easier to find projections of vectors on axes if the projected vectors are parallel or perpendicular to the selected axes. Please note that for the case of parallelism, two options are possible: the vector is co-directional to the axis and the vector is opposite to the axis, and for the case of perpendicularity there is only one option.
The projection of a vector perpendicular to the axis is always zero (see sy and ay in the left drawing, and sx and υx in the right drawing). Indeed, for a vector perpendicular to the axis, the angle between it and the axis is 90°, so the cosine is zero, which means the projection is zero.
The projection of a vector codirectional with the axis is positive and equal to its absolute value, for example, sx = +s (see left drawing). Indeed, for a vector codirectional with the axis, the angle between it and the axis is zero, and its cosine is “+1”, that is, the projection is equal to the length of the vector: sx = x – xo = +s .
The projection of the vector opposite to the axis is negative and equal to its absolute value, taken with a minus sign, for example, sy = –s (see the right drawing). Indeed, for a vector opposite to the axis, the angle between it and the axis is 180°, and its cosine is “–1”, that is, the projection is equal to the length of the vector taken with a negative sign: sy = y – yo = –s .
The right-hand sides of both drawings show other cases where the vectors are parallel to one of the coordinate axes and perpendicular to the other. We invite you to make sure for yourself that in these cases, too, the rules formulated in the previous paragraphs are followed.
