On this page you will find all the basic trigonometric formulas that will help you solve many exercises, greatly simplifying the expression itself.
Trigonometric formulas - mathematical equalities For trigonometric functions, which are executed for all valid argument values.
Formulas specify the relationships between the basic trigonometric functions - sine, cosine, tangent, cotangent.
The sine of an angle is the y coordinate of a point (ordinate) on unit circle. The cosine of an angle is the x coordinate of a point (abscissa).
Tangent and cotangent are, respectively, the ratios of sine to cosine and vice versa.
`sin\\alpha,\cos\\alpha`
`tg \ \alpha=\frac(sin\ \alpha)(cos \ \alpha),` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac(cos\ \alpha)(sin\ \alpha),` ` \alpha\ne\pi+\pi n, \ n \in Z`
And two that are used less often - secant, cosecant. They represent the ratios of 1 to cosine and sine.
`sec \ \alpha=\frac(1)(cos\ \alpha),` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac(1)(sin \ \alpha),` ` \alpha\ne\pi+\pi n,\ n \in Z`
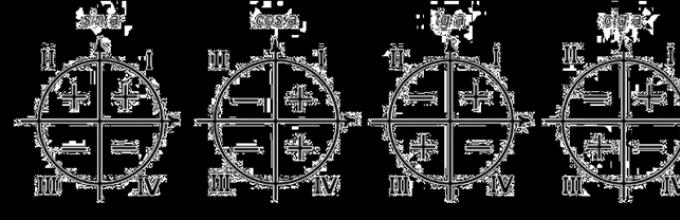
From the definitions of trigonometric functions it is clear what signs they have in each quadrant. The sign of the function depends only on which quadrant the argument is located in.

When changing the sign of the argument from “+” to “-”, only the cosine function does not change its value. It's called even. Its graph is symmetrical about the y-axis.
The remaining functions (sine, tangent, cotangent) are odd. When changing the sign of the argument from “+” to “-”, their value also changes to negative. Their graphs are symmetrical about the origin.
`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`
Basic trigonometric identities
Basic trigonometric identities are formulas that establish a connection between trigonometric functions of one angle (`sin\\\alpha,\cos\\alpha,\tg\\alpha,\ctg\\alpha`) and which allow you to find the value of each of these functions through any known other.
`sin^2 \alpha+cos^2 \alpha=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac(\pi n) 2, \n \in Z`
`1+tg^2 \alpha=\frac 1(cos^2 \alpha)=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n,\n \in Z`
`1+ctg^2 \alpha=\frac 1(sin^2 \alpha)=cosec^2 \alpha,` ` \alpha\ne\pi n, \n \in Z`
Formulas for the sum and difference of angles of trigonometric functions
Formulas for adding and subtracting arguments express trigonometric functions of the sum or difference of two angles in terms of trigonometric functions of these angles.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac(tg \ \alpha+tg \ \beta)(1-tg \ \alpha\ tg \ \beta)`
`tg(\alpha-\beta)=\frac(tg \ \alpha-tg \ \beta)(1+tg \ \alpha \ tg \ \beta)`
`ctg(\alpha+\beta)=\frac(ctg \ \alpha \ ctg \ \beta-1)(ctg \ \beta+ctg \ \alpha)`
`ctg(\alpha-\beta)=\frac(ctg \ \alpha\ ctg \ \beta+1)(ctg \ \beta-ctg \ \alpha)`
Double angle formulas
`sin \ 2\alpha=2 \ sin \ \alpha \cos \ \alpha=` `\frac (2 \ tg \ \alpha)(1+tg^2 \alpha)=\frac (2 \ ctg \ \alpha )(1+ctg^2 \alpha)=` `\frac 2(tg \ \alpha+ctg \ \alpha)`
`cos\2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \sin^2 \alpha=2 \cos^2 \alpha-1=` `\frac(1-tg^ 2\alpha)(1+tg^2\alpha)=\frac(ctg^2\alpha-1)(ctg^2\alpha+1)=` `\frac(ctg \ \alpha-tg \ \alpha) (ctg \ \alpha+tg \ \alpha)`
`tg \ 2\alpha=\frac(2 \ tg \ \alpha)(1-tg^2 \alpha)=` `\frac(2 \ ctg \ \alpha)(ctg^2 \alpha-1)=` `\frac 2(\ctg \ \alpha-tg \ \alpha)`
`ctg \ 2\alpha=\frac(ctg^2 \alpha-1)(2 \ctg \ \alpha)=` `\frac (\ctg \ \alpha-tg \ \alpha)2`
Triple angle formulas
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac(3 \ tg \ \alpha-tg^3 \alpha)(1-3 \ tg^2 \alpha)`
`ctg \ 3\alpha=\frac(ctg^3 \alpha-3 \ ctg \ \alpha)(3 \ ctg^2 \alpha-1)`
Half angle formulas
`sin \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)2)`
`cos \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \ \alpha)2)`
`tg \ \frac \alpha 2=\pm \sqrt(\frac (1-cos \ \alpha)(1+cos \ \alpha))=` `\frac (sin \ \alpha)(1+cos \ \ alpha)=\frac (1-cos \ \alpha)(sin \ \alpha)`
`ctg \ \frac \alpha 2=\pm \sqrt(\frac (1+cos \ \alpha)(1-cos \ \alpha))=` `\frac (sin \ \alpha)(1-cos \ \ alpha)=\frac (1+cos \ \alpha)(sin \ \alpha)`
Formulas for half, double and triple arguments express the functions `sin, \cos, \tg, \ctg` of these arguments (`\frac(\alpha)2, \2\alpha, \3\alpha,... `) through these functions argument `\alpha`.
Their conclusion can be obtained from the previous group (addition and subtraction of arguments). For example, double angle identities are easily obtained by replacing `\beta` with `\alpha`.
Degree reduction formulas
Formulas of squares (cubes, etc.) of trigonometric functions allow you to move from 2,3,... degrees to trigonometric functions of the first degree, but multiple angles (`\alpha, \3\alpha, \...` or `2\alpha, \ 4\alpha, \...`).
`sin^2 \alpha=\frac(1-cos \ 2\alpha)2,` ` (sin^2 \frac \alpha 2=\frac(1-cos \ \alpha)2)`
`cos^2 \alpha=\frac(1+cos \ 2\alpha)2,` ` (cos^2 \frac \alpha 2=\frac(1+cos \ \alpha)2)`
`sin^3 \alpha=\frac(3sin \ \alpha-sin \ 3\alpha)4`
`cos^3 \alpha=\frac(3cos \ \alpha+cos \ 3\alpha)4`
`sin^4 \alpha=\frac(3-4cos \ 2\alpha+cos \ 4\alpha)8`
`cos^4 \alpha=\frac(3+4cos \ 2\alpha+cos \ 4\alpha)8`
Formulas for the sum and difference of trigonometric functions
The formulas are transformations of the sum and difference of trigonometric functions of different arguments into a product.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac(\alpha+\beta)2 \ cos \frac(\alpha-\beta)2`
`sin \ \alpha-sin \ \beta=` `2 \cos \frac(\alpha+\beta)2 \sin \frac(\alpha-\beta)2`
`cos \ \alpha+cos \ \beta=` `2 \cos \frac(\alpha+\beta)2 \cos \frac(\alpha-\beta)2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac(\alpha+\beta)2 \ sin \frac(\alpha-\beta)2=` `2 \ sin \frac(\alpha+\ beta)2\sin\frac(\beta-\alpha)2`
`tg \ \alpha \pm tg \ \beta=\frac(sin(\alpha \pm \beta))(cos \ \alpha \ cos \ \beta)`
`ctg \ \alpha \pm ctg \ \beta=\frac(sin(\beta \pm \alpha))(sin \ \alpha \ sin \ \beta)`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac(cos(\alpha \mp \beta))(cos \ \alpha \ sin \ \beta)`
Here the transformation of addition and subtraction of functions of one argument into a product occurs.
`cos \ \alpha+sin \ \alpha=\sqrt(2) \cos (\frac(\pi)4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt(2) \ sin (\frac(\pi)4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ctg \2\alpha`
The following formulas convert the sum and difference of one and a trigonometric function into a product.
`1+cos \ \alpha=2 \cos^2 \frac(\alpha)2`
`1-cos \ \alpha=2 \ sin^2 \frac(\alpha)2`
`1+sin \ \alpha=2 \ cos^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1-sin \ \alpha=2 \ sin^2 (\frac (\pi) 4-\frac(\alpha)2)`
`1 \pm tg \ \alpha=\frac(sin(\frac(\pi)4 \pm \alpha))(cos \frac(\pi)4 \cos \ \alpha)=` `\frac(\sqrt (2) sin(\frac(\pi)4 \pm \alpha))(cos \ \alpha)`
`1 \pm tg \ \alpha \ tg \ \beta=\frac(cos(\alpha \mp \beta))(cos \ \alpha \ cos \ \beta);` ` \ctg \ \alpha \ctg \ \ beta \pm 1=\frac(cos(\alpha \mp \beta))(sin \ \alpha \ sin \ \beta)`
Formulas for converting products of functions
Formulas for converting the product of trigonometric functions with arguments `\alpha` and `\beta` into the sum (difference) of these arguments.
`sin \ \alpha \ sin \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(2)`
`sin\alpha \cos\beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(2)`
`cos \ \alpha \cos \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(2)`
`tg \ \alpha \ tg \ \beta =` `\frac(cos(\alpha - \beta)-cos(\alpha + \beta))(cos(\alpha - \beta)+cos(\alpha + \ beta)) =` `\frac(tg \ \alpha + tg \ \beta)(ctg \ \alpha + ctg \ \beta)`
`ctg \ \alpha \ ctg \ \beta =` `\frac(cos(\alpha - \beta)+cos(\alpha + \beta))(cos(\alpha - \beta)-cos(\alpha + \ beta)) =` `\frac(ctg \ \alpha + ctg \ \beta)(tg \ \alpha + tg \ \beta)`
`tg \ \alpha \ ctg \ \beta =` `\frac(sin(\alpha - \beta)+sin(\alpha + \beta))(sin(\alpha + \beta)-sin(\alpha - \ beta))`
Universal trigonometric substitution
These formulas express trigonometric functions in terms of the tangent of a half angle.
`sin \ \alpha= \frac(2tg\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha\ne \pi +2\ pi n, n \in Z`
`cos \ \alpha= \frac(1 - tg^(2)\frac(\alpha)(2))(1 + tg^(2)\frac(\alpha)(2)),` ` \alpha \ ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac(2tg\frac(\alpha)(2))(1 - tg^(2)\frac(\alpha)(2)),` ` \alpha \ne \pi +2\ pi n, n \in Z,` ` \alpha \ne \frac(\pi)(2)+ \pi n, n \in Z`
`ctg \ \alpha = \frac(1 - tg^(2)\frac(\alpha)(2))(2tg\frac(\alpha)(2)),` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`
Reduction formulas
Reduction formulas can be obtained using such properties of trigonometric functions as periodicity, symmetry, and the property of shifting by a given angle. They allow functions of an arbitrary angle to be converted into functions whose angle is between 0 and 90 degrees.
For angle (`\frac (\pi)2 \pm \alpha`) or (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
For angle (`\pi \pm \alpha`) or (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
For angle (`\frac (3\pi)2 \pm \alpha`) or (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 — \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 — \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
For angle (`2\pi \pm \alpha`) or (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Expressing some trigonometric functions in terms of others
`sin \ \alpha=\pm \sqrt(1-cos^2 \alpha)=` `\frac(tg \ \alpha)(\pm \sqrt(1+tg^2 \alpha))=\frac 1( \pm \sqrt(1+ctg^2 \alpha))`
`cos \ \alpha=\pm \sqrt(1-sin^2 \alpha)=` `\frac 1(\pm \sqrt(1+tg^2 \alpha))=\frac (ctg \ \alpha)( \pm \sqrt(1+ctg^2 \alpha))`
`tg \ \alpha=\frac (sin \ \alpha)(\pm \sqrt(1-sin^2 \alpha))=` `\frac (\pm \sqrt(1-cos^2 \alpha))( cos\\alpha)=\frac 1(ctg\\alpha)`
`ctg \ \alpha=\frac (\pm \sqrt(1-sin^2 \alpha))(sin \ \alpha)=` `\frac (cos \ \alpha)(\pm \sqrt(1-cos^ 2 \alpha))=\frac 1(tg \ \alpha)`
Trigonometry literally translates to “measuring triangles.” It begins to be studied at school, and continues in more detail at universities. Therefore, basic formulas in trigonometry are needed starting from grade 10, as well as for passing the Unified State Exam. They denote connections between functions, and since there are many of these connections, there are many formulas themselves. It is not easy to remember them all, and it is not necessary - if necessary, they can all be displayed.
Trigonometric formulas are used in integral calculus, as well as in trigonometric simplifications, calculations, transformations.
Exercise.
Find the value of x at .
Solution.
Finding the value of the function argument at which it is equal to any value means determining at which arguments the value of the sine will be exactly as indicated in the condition.
In this case, we need to find out at what values the sine value will be equal to 1/2. This can be done in several ways.
For example, use , by which to determine at what values of x the sine function will be equal to 1/2.
Another way is to use . Let me remind you that the values of the sines lie on the Oy axis.
The most common way is to use , especially when dealing with values that are standard for this function, such as 1/2.
In all cases, one should not forget about one of the most important properties of the sine - its period.
Let's find the value 1/2 for sine in the table and see what arguments correspond to it. The arguments we are interested in are Pi / 6 and 5Pi / 6.
Let us write down all the roots that satisfy given equation. To do this, we write down the unknown argument x that interests us and one of the values of the argument obtained from the table, that is, Pi / 6. We write down for it, taking into account the period of the sine, all the values of the argument:
![]()
Let's take the second value and follow the same steps as in the previous case:
![]()
The complete solution to the original equation will be: ![]() And
And ![]()
q can take the value of any integer.
In trigonometry, many formulas are easier to derive than to memorize. Cosine of double angle is a wonderful formula! It allows you to obtain formulas for reducing degrees and formulas for half angles.
So, we need the cosine of the double angle and the trigonometric unit:
They are even similar: in the double angle cosine formula it is the difference between the squares of the cosine and sine, and in the trigonometric unit it is their sum. If we express the cosine from the trigonometric unit:
and substitute it into the cosine of the double angle, we get:
This is another double angle cosine formula:
This formula is the key to obtaining the reduction formula:
So, the formula for reducing the degree of sine is:
![]()
If the alpha angle in it is replaced by half the alpha angle in half, and double angle two alphas per angle alpha, we get the half-angle formula for sine:
![]()
Now we can express the sine from the trigonometric unit:
Let's substitute this expression into the double angle cosine formula:
![]()
We got another formula for the cosine of a double angle:
This formula is the key to finding the formula for reducing the power of cosine and the half angle for cosine.
Thus, the formula for reducing the degree of cosine is:
![]()
If we replace α with α/2, and 2α with α, we obtain the formula for the half argument for the cosine:
![]()
Since tangent is the ratio of sine to cosine, the formula for tangent is:
![]()
Cotangent is the ratio of cosine to sine. Therefore, the formula for cotangent is:
![]()
Of course, in the process of simplifying trigonometric expressions, there is no point in deriving the formula for half an angle or reducing a degree every time. It is much easier to put a sheet of paper with formulas in front of you. And simplification will move faster, and visual memory will turn on memorization.
But it’s still worth deriving these formulas several times. Then you will be absolutely sure that during the exam, when it is not possible to use a cheat sheet, you will easily get them if the need arises.