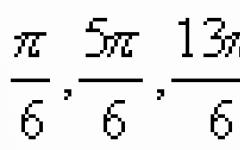In mechanics, external forces in relation to a given system of material points (i.e., such a set of material points in which the movement of each point depends on the positions or movements of all other points) are those forces that represent the action of other bodies on this system (other systems of material points) not included by us in this system. Internal forces are the forces of interaction between individual material points of a given system. The division of forces into external and internal is completely conditional: when the given composition of the system changes, some forces that were previously external can become internal, and vice versa. So, for example, when considering
the movement of a system consisting of the earth and its satellite the moon, the interaction forces between these bodies will be internal forces for this system, and the gravitational forces of the sun, the remaining planets, their satellites and all the stars will be external forces in relation to the specified system. But if we change the composition of the system and consider the movement of the sun and all the planets as the movement of one common system, then external the forces will be only the forces of attraction exerted by the stars; nevertheless, the forces of interaction between the planets, their satellites and the sun become internal forces for this system. In exactly the same way, if, when a steam locomotive is moving, we select the piston of the steam cylinder as separate system material points subject to our consideration, then the steam pressure on the piston in relation to it will be external force, and the same vapor pressure will be one of internal forces, if we consider the movement of the entire locomotive as a whole; in this case, external forces in relation to the entire locomotive, taken as one system, will be: friction between the rails and wheels of the locomotive, gravity of the locomotive, reaction of the rails and air resistance; internal forces will be all the forces of interaction between parts of the locomotive, for example. interaction forces between steam and the cylinder piston, between the slider and its parallels, between the connecting rod and the crank pin, etc. As we see, there is essentially no difference between external and internal forces, the relative difference between them is determined only depending on which bodies we include in the system under consideration and which we consider not included in the system. However, the indicated relative difference in forces is very significant when studying the motion of a given system; according to Newton’s third law (on the equality of action and reaction), the internal forces of interaction between each two material points of the system are equal in magnitude and directed along the same straight line in opposite directions; Thanks to this, when resolving various questions about the motion of a system of material points, it is possible to exclude all internal forces from the equations of motion of the system and thereby make possible the study of the motion of the entire system. This method of eliminating internal, in most cases unknown, coupling forces is essential in deriving various laws of mechanics of a system.
Absolutely elastic impact- a collision of two bodies, as a result of which no deformations remain in both bodies participating in the collision and all the kinetic energy of the bodies before the impact after the impact again turns into the original kinetic energy (note that this is an idealized case).
For an absolutely elastic impact, the law of conservation of kinetic energy and the law of conservation of momentum are satisfied.
Let us denote the velocities of the balls with masses m 1 and m 2 before impact through ν 1 And ν 2, after impact - through ν 1 " And ν 2"(Fig. 1). For a direct central impact, the velocity vectors of the balls before and after the impact lie on a straight line passing through their centers. The projections of the velocity vectors onto this line are equal to the velocity modules. We will take their directions into account using signs: positive ones will be associated with movement to the right, negative ones with movement to the left.
Fig.1
Under these assumptions, the conservation laws have the form
(1)
(2)
Having made the appropriate transformations in expressions (1) and (2), we obtain
(3)
(4)
Solving equations (3) and (5), we find
(7)
Let's look at a few examples.
1. When ν 2=0
(8) 
(9)
Let us analyze expressions (8) in (9) for two balls of different masses:
a) m 1 = m 2. If the second ball was hanging motionless before the impact ( ν 2=0) (Fig. 2), then after the impact the first ball will stop ( ν 1 "=0), and the second one will move with the same speed and in the same direction in which the first ball was moving before the impact ( ν 2"=ν 1);
Fig.2
b) m 1 >m 2. The first ball continues to move in the same direction as before the impact, but at a lower speed ( ν 1 "<ν 1). The speed of the second ball after impact is greater than the speed of the first ball after impact ( ν 2">ν 1 ") (Fig. 3);
Fig.3
c) m 1
Fig.4
d) m 2 >>m 1 (for example, a collision of a ball with a wall). From equations (8) and (9) it follows that ν 1 "= -ν 1; ν 2"≈ 2m 1 ν 2"/m 2 .
2. When m 1 =m 2 expressions (6) and (7) will have the form ν 1 "= ν 2; ν 2"= ν 1; that is, balls of equal mass seem to exchange velocities.
Absolutely inelastic impact- a collision of two bodies, as a result of which the bodies connect, moving further as a single whole. An absolutely inelastic impact can be demonstrated using plasticine (clay) balls that move towards each other (Fig. 5).
Fig.5
If the masses of the balls are m 1 and m 2, their velocities before impact ν 1 And ν 2, then, using the law of conservation of momentum
Where v- the speed of movement of the balls after impact. Then
(15.10)
If the balls move towards each other, they will together continue to move in the direction in which the ball moved with high momentum. In the particular case, if the masses of the balls are equal (m 1 =m 2), then
Let us determine how the kinetic energy of the balls changes during a central absolutely inelastic impact. Since during the collision of balls between them there are forces that depend on their velocities, and not on the deformations themselves, we are dealing with dissipative forces similar to friction forces, therefore the law of conservation of mechanical energy in this case should not be observed. Due to deformation, there is a decrease in kinetic energy, which turns into thermal or other forms of energy. This decrease can be determined by the difference in the kinetic energy of the bodies before and after the impact:
Using (10), we obtain
If the impacted body was initially motionless (ν 2 =0), then
When m 2 >>m 1 (the mass of the stationary body is very large), then ν <<ν 1 and practically all the kinetic energy of the body is converted into other forms of energy upon impact. Therefore, for example, to obtain significant deformation, the anvil must be significantly more massive than the hammer. On the contrary, when hammering nails into a wall, the mass of the hammer should be much greater (m 1 >>m 2), then ν≈ν 1 and almost all the energy is spent on moving the nail as much as possible, and not on residual deformation of the wall.
A completely inelastic impact is an example of the loss of mechanical energy under the influence of dissipative forces.
1. Work of variable force.
Let us consider a material point moving under the influence of force P in a straight line. If effective force is constant and directed along a straight line, and the displacement is equal to s, then, as is known from physics, the work A of this force is equal to the product Ps. Now let's derive a formula for calculating the work done by a variable force.
Let a point move along the Ox axis under the influence of a force, the projection of which onto the Ox axis is a function of f from x. In this case we will assume that f is continuous function. Under the influence of this force, the material point moved from point M (a) to point M (b) (Fig. 1, a). Let us show that in this case the work of A is calculated by the formula
(1)
Let's split the segment [a; b] into n segments of the same length. These are the segments [a; x 1 ], ,..., (Fig. 1.6). Work of force on the entire segment [a; b] is equal to the sum of the work done by this force on the resulting segments. Since f is a continuous function of x, for a sufficiently small segment [a; x 1 ] the work done by the force on this segment is approximately equal to f (a) (x 1 -a) (we neglect the fact that f changes on the segment). Similarly, the work done by the force on the second segment is approximately equal to f (x 1) (x 2 - x 1), etc.; the work done by the force on the nth segment is approximately equal to f (x n-1)(b - x n-1). Consequently, the work of force on the entire segment [a; b] is approximately equal to:
and the accuracy of the approximate equality is higher, the shorter the segments into which the segment [a;b] is divided. Naturally, this approximate equality becomes exact if we assume that n→∞:
Since A n tends to the integral of the function under consideration from a to b as n →∞, formula (1) is derived.
2. Power.
Power P is the rate of work done,
Here v is speed material point, to which the force is applied
All forces encountered in mechanics are usually divided into conservative and non-conservative.
A force acting on a material point is called conservative (potential) if the work done by this force depends only on the initial and final positions of the point. The work of a conservative force does not depend either on the type of trajectory or on the law of motion of a material point along the trajectory (see Fig. 2): 
.
Changing the direction of movement of a point along a small area to the opposite causes a change in the sign of the elementary work, therefore, . Therefore, the work of a conservative force along a closed trajectory 1 a 2b 1 equals zero: 
.
Points 1 and 2, as well as sections of closed trajectory 1 a 2 and 2 b 1 can be chosen completely arbitrarily. Thus, the work of a conservative force along an arbitrary closed trajectory L of the point of its application is equal to zero:
In this formula, the circle on the integral sign shows that the integration is carried out along a closed path. Often a closed trajectory L called a closed loop L(Fig. 3). Usually specified by the direction of traversal of the contour L clockwise. The direction of the elementary displacement vector coincides with the direction of the contour traversal L. In this case, formula (5) states: circulation of the vector along a closed loop L is equal to zero.
It should be noted that the forces of gravity and elasticity are conservative, and the forces of friction are non-conservative. In fact, since the friction force is directed in the direction opposite to the displacement or speed, the work of the friction forces along a closed path is always negative and, therefore, not equal to zero.
Dissipative system(or dissipative structure, from lat. dissipatio- “disperse, destroy”) is an open system that operates far from thermodynamic equilibrium. In other words, this is a stable state that arises in a nonequilibrium environment under the condition of dissipation (dissipation) of energy that comes from outside. A dissipative system is sometimes also called stationary open system or nonequilibrium open system.
A dissipative system is characterized by the spontaneous appearance of a complex, often chaotic structure. Distinctive feature such systems - non-conservation of volume in phase space, that is, non-fulfillment of Liouville's Theorem.
A simple example Such a system is Benard cells. As more complex examples called lasers, the Belousov-Zhabotinsky reaction and biological life.
The term “dissipative structure” was introduced by Ilya Prigogine.
Recent research in the field of “dissipative structures” allows us to conclude that the process of “self-organization” occurs much faster in the presence of external and internal “noise” in the system. Thus, noise effects lead to an acceleration of the “self-organization” process.
Kinetic energy
energy mechanical system, depending on the speed of movement of its points. K. e. T material point is measured by half the product of mass m of this point by the square of its speed υ, i.e. T = 1/ 2 mυ 2 . K. e. mechanical system is equal to arithmetic sum K. e. all its points: T =Σ 1 / 2 m k υ 2 k . Expression K. e. systems can also be represented in the form T = 1 / 2 Mυ s 2 + Tc, Where M- mass of the entire system, υ c- speed of the center of mass, Tc - K. e. system in its motion around the center of mass. K. e. solid, moving translationally, is calculated in the same way as K. e. a point with mass equal to mass whole body. Formulas for calculating K. e. of a body rotating around a fixed axis, see Art. Rotational movement.
Change in K. e. system when it is moved from its position (configuration) 1
to position 2
occurs under the influence of external and internal forces applied to the system and is equal to the sum of work 
.
This equality expresses the theorem on the change of the dynamic energy, with the help of which many problems of dynamics are solved.
At speeds close to the speed of light, K. e. material point
Where m 0- mass of a point at rest, With- speed of light in vacuum ( m 0 s 2- energy of a point at rest). At low speeds ( υ<< c ) the last relation goes into the usual formula 1 / 2 mυ 2.
Kinetic energy.
Kinetic energy - energy of a moving body. (From the Greek word kinema - movement). By definition, the kinetic energy of a body at rest in a given frame of reference vanishes.
Let the body move under the influence constant force in the direction of the force.
Then: 
.
Because motion is uniformly accelerated, then: .
Hence: 
.
- kinetic energy is called
Forces acting on any point of a mechanical system are divided into internal and external.
Fi– inner strength
Fe– external force
Internal are called the forces with which the points included in the system act on each other.
External are called forces that are applied to points from the outside, that is, from other points or bodies not included in the system. The division of forces into internal and external is conditional.
mg – external force
Ftr – internal strength
Mechanical system. External and internal forces.
A mechanical system of material points or bodies is a collection of them in which the position or movement of each point (or body) depends on the position and movement of all the others.
We will also consider a material absolutely solid body as a system of material points that form this body and are interconnected in such a way that the distances between them do not change and remain constant all the time.
A classic example of a mechanical system is the solar system, in which all bodies are connected by forces of mutual attraction. Another example of a mechanical system is any machine or mechanism in which all the bodies are connected by hinges, rods, cables, belts, etc. (i.e. various geometric connections). In this case, the bodies of the system are subject to mutual pressure or tension forces transmitted through connections.
A collection of bodies between which there are no interaction forces (for example, a group of airplanes flying in the air) does not form a mechanical system.
In accordance with what has been said, the forces acting on points or bodies of the system can be divided into external and internal.
External forces are those acting on points of a system from points or bodies that are not part of the given system.
Internal forces are those acting on points of a system from other points or bodies of the same system. We will denote external forces by the symbol - , and internal forces by - .
Both external and internal forces can, in turn, be either active or reactions of connections.
Reactions of connections, or simply reactions, are forces that limit the movement of points in the system (their coordinates, speed, etc.). In statics these were forces replacing connections. In dynamics, a more general definition is introduced for them.
All other forces are called active or given forces, everything except reactions.
The necessity of this classification of forces will become clear in the following chapters.
The division of forces into external and internal is conditional and depends on the movement of which system of bodies we are considering. For example, if we consider the movement of the entire solar system as a whole, then the force of attraction of the Earth to the Sun will be internal; when studying the movement of the Earth in its orbit around the Sun, the same force will be considered as external.
Internal forces have the following properties:
1. The geometric sum (principal vector) of all internal forces F12 and F21 of the system is equal to zero. In fact, according to the third law of dynamics, any two points of the system (Fig. 31) act on each other with equal magnitude and oppositely directed forces and, the sum of which is equal to zero. Since a similar result holds for any pair of points in the system, then
2. The sum of moments (principal moment) of all internal forces of the system relative to any center or axis is equal to zero. Indeed, if we take an arbitrary center O, then from Fig. 18 it is clear that . A similar result will be obtained when calculating the moments about the axis. Therefore, for the entire system there will be:
However, it does not follow from the proven properties that the internal forces are mutually balanced and do not affect the movement of the system, since these forces are applied to different material points or bodies and can cause mutual movements of these points or bodies. The internal forces will be balanced when the system under consideration is an absolutely rigid body.
30Theorem on the movement of the center of mass.
System weight equals the algebraic sum of the masses of all points or bodies of the system in a uniform gravitational field, for which the weight of any particle of the body is proportional to its mass. Therefore, the distribution of masses in a body can be determined by the position of its center of gravity - geometric point C, the coordinates of which are called the center of mass or center of inertia of a mechanical system
Theorem on the motion of the center of mass of a mechanical system : the center of mass of a mechanical system moves as a material point whose mass is equal to the mass of the system, and to which all external forces acting on the system are applied
Conclusions:
A mechanical system or a rigid body can be considered as a material point depending on the nature of its motion, and not on its size.
Internal forces are not taken into account by the theorem on the motion of the center of mass.
The theorem on the motion of the center of mass does not characterize the rotational motion of a mechanical system, but only the translational one
Law on the conservation of motion of the center of mass of the system:
1. If the sum of external forces (the main vector) is constantly equal to zero, then the center of mass of the mechanical system is at rest or moves uniformly and rectilinearly.
2. If the sum of the projections of all external forces onto any axis is equal to zero, then the projection of the velocity of the center of mass of the system onto the same axis is a constant value.
The equation expresses the theorem on the motion of the center of mass of the system: the product of the mass of the system and the acceleration of its center of mass is equal to the geometric sum of all external forces acting on the system. Comparing with the equation of motion of a material point, we obtain another expression of the theorem: the center of mass of the system moves as a material point, the mass of which is equal to the mass of the entire system and to which all external forces acting on the system are applied.
If expression (2) is placed in (3), taking into account the fact that we get:
(4’) – expresses the theorem on the movement of the center of mass of the system: the center of mass of the system moves as a material point on which all the forces of the system act.
Conclusions:
1. Internal forces do not affect the movement of the center of mass of the system.
2. If , the movement of the center of mass of the system occurs at a constant speed.
3., then the movement of the center of mass of the system in projection onto the axis occurs at a constant speed.
These equations are differential equations of motion of the center of mass in projections on the axes of the Cartesian coordinate system.
The meaning of the proven theorem is as follows.
1) The theorem provides justification for the methods of point dynamics. From the equations it is clear that the solutions that we obtain by considering a given body as a material point determine the law of motion of the center of mass of this body, i.e. have a very specific meaning.
In particular, if a body moves translationally, then its motion is completely determined by the movement of the center of mass. Thus, a translationally moving body can always be considered as a material point with a mass equal to the mass of the body. In other cases, a body can be considered as a material point only when, practically, to determine the position of the body it is enough to know the position of its center of mass.
2) The theorem allows, when determining the law of motion of the center of mass of any system, to exclude from consideration all previously unknown internal forces. This is its practical value.
Thus, the movement of a car on a horizontal plane can only occur under the influence of external forces, friction forces acting on the wheels from the road. And braking a car is also possible only with these forces, and not with friction between the brake pads and the brake drum. If the road is smooth, then no matter how much you brake the wheels, they will slide and will not stop the car.
Or after the explosion of a flying projectile (under the influence of internal forces), its parts, fragments, will scatter so that their center of mass will move along the same trajectory.
The theorem on the motion of the center of mass of a mechanical system should be used to solve problems of mechanics that require:
Using the forces applied to a mechanical system (most often to a solid body), determine the law of motion of the center of mass;
According to the given law of motion of bodies included in a mechanical system, find the reactions of external connections;
Based on the given mutual motion of the bodies included in the mechanical system, determine the law of motion of these bodies relative to some fixed reference system.
Using this theorem, you can create one of the equations of motion of a mechanical system with several degrees of freedom.
When solving problems, corollaries from the theorem on the motion of the center of mass of a mechanical system are often used.
Corollary 1. If the main vector of external forces applied to a mechanical system is equal to zero, then the center of mass of the system is at rest or moves uniformly and rectilinearly. Since the acceleration of the center of mass is zero, .
Corollary 2. If the projection of the main vector of external forces onto any axis is zero, then the center of mass of the system either does not change its position relative to this axis or moves uniformly relative to it.
For example, if two forces begin to act on a body, forming a pair of forces (Fig. 38), then its center of mass C will move along the same trajectory. And the body itself will rotate around the center of mass. And it doesn’t matter where the couple of forces are applied.
Mechanical system is a collection of material points or bodies in which the position or movement of each point or body depends on the position and movement of all the others. So, for example, when studying the movement of the Earth and the Moon relative to the Sun, the totality of the Earth and the Moon is a mechanical system consisting of two material points; when a projectile breaks into fragments, we consider the fragments as a mechanical system. A mechanical system is any mechanism or machine.
If the distances between points of a mechanical system do not change when the system is moving or at rest, then such a mechanical system is called immutable.
The concept of an unchangeable mechanical system makes it possible to study the arbitrary motion of solid bodies in dynamics. In this case, as in statics and kinematics, by a rigid body we will understand a material body in which the distance between each two points does not change when the body moves or rests. Any solid body can be mentally divided into a sufficiently large number of sufficiently small parts, the totality of which can be approximately considered as a mechanical system. Since a solid body forms a continuous extension, in order to establish its exact (and not approximate) properties it is necessary to make a limiting transition, the ultimate fragmentation of the body, when the sizes of the considered parts of the body simultaneously tend to zero.
Thus, knowledge of the laws of motion of mechanical systems allows us to study the laws of arbitrary motion of solid bodies.
All forces acting on points of a mechanical system are divided into external and internal forces.
External forces in relation to a given mechanical system are forces acting on points of this system from material points or bodies not included in the system. Designations: - external force applied to the th point; 
-the main vector of external forces; 
- the main moment of external forces relative to the pole.
Internal forces are the forces with which material points or bodies included in a given mechanical system act on points or bodies of the same system. In other words, internal forces are the forces of interaction between points or bodies of a given mechanical system. Designations: - internal force applied to the th point; 
-the main vector of internal forces; 
- the main moment of internal forces relative to the pole.
3.2 Properties of internal forces.
First property.The main vector of all internal forces of a mechanical system is equal to zero, that is
. (3.1)
Second property.The main moment of all internal forces of a mechanical system relative to any pole or axis is equal to zero, that is
, 
. (3.2)
|
To prove these properties, we note that since internal forces are the forces of interaction of material points included in the system, then according to Newton’s third law, any two points of the system (Fig. 17) act on each other with forces and equal in magnitude and opposite in direction. Thus, for each internal force there is a directly opposite internal force and, therefore, the internal forces form a certain set of pairwise opposite forces. But the geometric sum of two directly opposite forces is zero, so
.
As was shown in statics, the geometric sum of the moments of two directly opposite forces relative to the same pole is equal to zero, therefore
.
A similar result is obtained when calculating the main moment about the axis
.
3.3 Differential equations of motion of a mechanical system.
Let us consider a mechanical system consisting of material points whose masses are . For each point we apply the basic equation of point dynamics
, 
,
, (3.3)
de is the resultant of external forces applied to the th point, and is the resultant of internal forces.
The system of differential equations (3.3) is called differential equations of motion of a mechanical system in vector form.
Projecting vector equations (3.3) onto rectangular Cartesian coordinate axes we obtain differential equations of motion of a mechanical system in coordinate form:
,
, (3.4)
,
.
These equations are a system of second order ordinary differential equations. Consequently, to find the motion of a mechanical system according to given forces and initial conditions for each point of this system, it is necessary to integrate a system of differential equations. Integrating the system of differential equations (3.4), generally speaking, is associated with significant, often insurmountable, mathematical difficulties. However, in theoretical mechanics, methods have been developed that make it possible to circumvent the main difficulties that arise when using differential equations of motion of a mechanical system in the form (3.3) or (3.4). These include methods that provide general theorems for the dynamics of a mechanical system, establishing the laws of change in some total (integral) characteristics of the system as a whole, and not the patterns of movement of its individual elements. These are the so-called measures of motion - the main vector of momentum; principal moment of momentum; kinetic energy. Knowing the nature of the change in these quantities, it is possible to form a partial, and sometimes complete, picture of the movement of a mechanical system.
IV. BASIC (GENERAL) THEOREMS OF DYNAMICS OF A POINT AND SYSTEM
4.1 Theorem on the motion of the center of mass.
4.1.1. Center of mass of a mechanical system.
Let us consider a mechanical system consisting of material points whose masses are .
The mass of the mechanical system, consisting of material points, we will call the sum of the masses of the points of the system:
Definition. The center of mass of a mechanical system is a geometric point, the radius vector of which is determined by the formula:
where is the radius vector of the center of mass; -radius vectors of system points; -their masses (Fig. 18).
; 
; . (4.1")
The center of mass is not a material point, but geometric. It may not coincide with any material point of the mechanical system. In a uniform gravity field, the center of mass coincides with the center of gravity. This does not mean, however, that the concepts of center of mass and center of gravity are the same. The concept of the center of mass is applicable to any mechanical systems, and the concept of the center of gravity is applicable only to mechanical systems that are under the influence of gravity (that is, attraction to the Earth). So, for example, in celestial mechanics, when considering the problem of the motion of two bodies, for example the Earth and the Moon, one can consider the center of mass of this system, but one cannot consider the center of gravity.
Thus, the concept of center of mass is broader than the concept of center of gravity.
4.1.2. Theorem on the motion of the center of mass of a mechanical system.
Theorem. The center of mass of a mechanical system moves as a material point, the mass of which is equal to the mass of the entire system and to which all external forces acting on the system are applied, that is
.
(4.2)
Here -the main vector of external forces.
Proof. Let us consider a mechanical system, the material points of which move under the influence of external and internal forces. is the resultant of external forces applied to the th point, and is the resultant of internal forces. According to (3.3), the equation of motion of the th point has the form
, .
Adding the left and right sides of these equations, we get
.
Since the main vector of internal forces is equal to zero (section 3.2, first property), then
.
Let's transform the left side of this equality. From formula (4.1), which determines the radius vector of the center of mass, it follows:
.
Throughout the following we will assume that only mechanical systems of constant composition are considered, that is, and . Let us take the second derivative with respect to time from both sides of this equality
Because 
, -
acceleration of the center of mass of the system, then, finally,
.
Projecting both sides of this vector equality onto the coordinate axes, we obtain:
,
, (4.3)
,
where , , are projections of force;
Projections of the main vector of external forces on the coordinate axes.
Equations (4.3)- differential equations of motion of the center of mass of a mechanical system in projections onto Cartesian coordinate axes.
From equations (4.2) and (4.3) it follows that Internal forces alone cannot change the nature of the movement of the center of mass of a mechanical system. Internal forces can have an indirect effect on the movement of the center of mass only through external forces. For example, in a car, the internal forces developed by the engine influence the movement of the center of mass through the friction forces of the wheels and the road.
4.1.3. Laws of conservation of motion of the center of mass
(corollaries from the theorem).
From the theorem on the motion of the center of mass, the following corollaries can be obtained.
Corollary 1.If the main vector of external forces acting on the system is zero, then its center of mass is at rest or moves rectilinearly and uniformly.
Indeed, if the main vector of external forces is , then from equation (4.2):
If, in particular, the initial velocity of the center of mass is , then the center of mass is at rest. If the initial speed is , then the center of mass moves rectilinearly and uniformly.
Corollary 2.If the projection of the main vector of external forces onto any fixed axis is zero, then the projection of the velocity of the center of mass of the mechanical system onto this axis does not change.
This consequence follows from equations (4.3). Let, for example, then
,
from here. If at the initial moment , then:
that is, the projection of the center of mass of the mechanical system onto the axis in this case will not move along the axis. If , then the projection of the center of mass onto the axis moves uniformly.
4.2 The amount of motion of a point and a system.
Theorem on the change of momentum.
4.2.1. The amount of motion of a point and a system.
Definition. The quantity of motion of a material point is a vector equal to the product of the mass of the point and its speed, that is
. (4.5)
Vector collinear to the vector and directed tangentially to the trajectory of the material point (Fig. 19).
The momentum of a point in physics is often called impulse of a material point.
The dimension of momentum in SI is kg·m/s or N·s.
Definition. The quantity of motion of a mechanical system is a vector equal to the vector sum of the quantities of movements (the main vector of the quantities of movements) of individual points included in the system, that is
(4.6)
Projections of momentum onto rectangular Cartesian coordinate axes:
Momentum vector of the system unlike the momentum vector of a point, it does not have a point of application. The momentum vector of a point is applied at the most moving point, and the vector is a free vector.
Lemma of quantities of motion. The momentum of a mechanical system is equal to the mass of the entire system multiplied by the speed of its center of mass, that is
Proof. From formula (4.1), which determines the radius vector of the center of mass, it follows:
.
Let us take the time derivative of both sides
, or 
.
From here we get
, which was what needed to be proven.
From formula (4.8) it is clear that if a body moves in such a way that its center of mass remains motionless, then the momentum of the body is zero. For example, the amount of motion of a body rotating around a fixed axis passing through its center of mass (Fig. 20),
, because
If the motion of the body is plane-parallel, then the amount of motion will not characterize the rotational part of the motion around the center of mass. For example, for a wheel that is rolling (Fig. 21), regardless of how the wheel rotates around the center of mass. The amount of motion characterizes only the translational part of the movement together with the center of mass.
4.2.2. Theorem on the change in momentum of a mechanical system
in differential form.
Theorem.The time derivative of the momentum of a mechanical system is equal to the geometric sum (principal vector) of external forces acting on this system, i.e.
.
(4.9)
Proof. Let us consider a mechanical system consisting of material points whose masses are ; -resultant of external forces applied to the th point. In accordance with the momentum lemma, formula (4.8):
Let us take the derivative with respect to time from both sides of this equality
.
The right side of this equality from the theorem on the motion of the center of mass is formula (4.2):
.
Finally:
and the theorem is proven .
In projections onto rectangular Cartesian coordinate axes:
; 
; 
, (4.10)
that is the time derivative of the projection of the momentum of a mechanical system onto any coordinate axis is equal to the sum of the projections (projection of the main vector) of all external forces of the system onto the same axis.
4.2.3. Laws of conservation of momentum
(corollaries from the theorem)
Corollary 1.If the main vector of all external forces of a mechanical system is equal to zero, then the amount of motion of the system is constant in magnitude and direction.
Indeed, if 
,
then from the theorem on the change in momentum, i.e. from equality (4.9) it follows that
Corollary 2.If the projection of the main vector of all external forces of a mechanical system onto a certain fixed axis is equal to zero, then the projection of the momentum of the system onto this axis remains constant.
Let the projection of the main vector of all external forces onto the axis be equal to zero: 
. Then from the first equality (4.10):
4.2.4. Theorem on the change in momentum of a mechanical system
in an integral form.
An elementary impulse of force is called a vector quantity equal to the product of the force vector and an elementary time interval
. (4.11)
The direction of the elementary impulse coincides with the direction of the force vector.
Force impulse over a finite period of time equal to a certain integral of the elementary momentum
. (4.12)
If the force is constant in magnitude and direction (), then its impulse over time equal to:
Projections of the force impulse on the coordinate axes:
Let us prove the theorem about the change in momentum of a mechanical system in integral form.
Theorem.The change in the momentum of a mechanical system over a certain period of time is equal to the geometric sum of the impulses of the external forces of the system over the same period of time, i.e.
(4.14)
Proof. Let at the moment of time the amount of motion of the mechanical system be equal, and at the moment of time -; -impulse of an external force acting on the th point in time.
We use the theorem on the change in momentum in differential form - equality (4.9):
.
Multiplying both sides of this equality by and integrating over the range from to , we obtain
, 
, 
.
The theorem on the change in momentum in integral form has been proven.
In projections on the coordinate axes according to (4.14):
,
, (4.15)
.
4.3. Theorem on the change in angular momentum.
4.3.1. Kinetic moment of a point and a system.
In statics, the concepts of moments of force relative to the pole and axis were introduced and widely used. Since the momentum of a material point is a vector, it is possible to determine its moments relative to the pole and axis in the same way as the moments of force are determined.
Definition. relative to the pole is called the moment of its vector of momentum relative to the same pole, i.e.
. (4.16)
Momentum of a material point relative to the pole is a vector (Fig. 22) directed perpendicular to the plane containing the vector and the pole in the direction from which the vector is relative to the pole visible in a counterclockwise direction. Vector module
equal to the product of the module and the arm - the length of the perpendicular lowered from the pole on the line of action of the vector:
The angular momentum relative to the pole can be represented as a vector product: the angular momentum of a material point relative to the pole is equal to the vector product of the radius of the vector drawn from the pole to the point by the momentum vector:
(4.17)
Definition. Kinetic moment of a material point relatively axis is called the moment of its vector of momentum relative to the same axis, i.e.
. (4.18)
Kinetic moment of a material point relative to the axis (Fig. 23) is equal to the product of the projection of the vector taken with a plus or minus sign onto a plane perpendicular to the axis , on the shoulder of this projection:
where shoulder is the length of the perpendicular dropped from the point axis intersections with the plane on the line of action of the projection, and if, looking towards the axis , the projection relative to the point is visible directed counterclockwise, and otherwise.
The dimension of the kinetic moment in SI-kg m 2 /s, or N m s.
Definition. The kinetic moment or principal moment of momentum of a mechanical system relative to a pole is a vector equal to the geometric sum of the kinetic moments of all material points of the system relative to this pole:
.
(4.19)
Definition. The kinetic moment or principal moment of momentum of a mechanical system relative to an axis is the algebraic sum of the kinetic moments of all material points of the system relative to this axis:
. (4.20)
The kinetic moments of a mechanical system relative to a pole and an axis passing through this pole are related by the same dependence as the main moments of a system of forces relative to the pole and axis:
-projection of the kinetic moment of a mechanical system relative to the pole onto the axis ,passing through this pole is equal to the angular momentum of the system relative to this axis, i.e.
. (4.21)
4.3.2. Theorems on the change in the kinetic moment of a mechanical system.
Let us consider a mechanical system consisting of material points whose masses are . Let's prove the theorem on the change in the angular momentum of a mechanical system relative to the pole.
Theorem.The time derivative of the kinetic moment of a mechanical system relative to a fixed pole is equal to the main moment of the external forces of the system relative to the same pole, i.e.
.
(4.22)
Proof. Let us choose some fixed pole . The kinetic moment of the mechanical system relative to this pole, by definition, is equality (4.19):
.
Let's differentiate this expression with respect to time:
Let's look at the right side of this expression. Calculating the derivative of the product:
, (4.24)
It is taken into account here that . Vectors and have the same direction, their vector product is equal to zero, therefore, the first sum in equality (4.24).
External forces are those acting on a body from points or bodies that are not part of the given body or system. Internal forces are those with which the points of a given body act on each other.
Destruction or even simple failure of a structural element is possible only with an increase in internal forces and when they pass through a certain limiting barrier. It is convenient to calculate the height of this barrier from the level that corresponds to the absence of external forces. Essentially, only additional internal forces that arise only in the presence of external forces need to be taken into account. In mechanics, these additional internal forces are simply called internal forces in the narrow, mechanical sense.
Internal forces are determined using the “method of sections”, which is based on a fairly obvious statement: if the body as a whole is in equilibrium, then any part isolated from it is also in this state
Figure 2.1.5
Let us consider a rod in equilibrium under the action of a system of external forces, Fig. 2.1.5, a. Let us mentally divide it into two parts using section AB, Fig. 2.1.5, b. To each of the sections AB of the left and right parts we will apply a system of forces corresponding to the internal forces acting in a real body, Fig. 1.7, c. Thus, using the method of sections, internal forces are converted into external forces in relation to each of the cut off parts of the body, which makes it possible to determine them from the equilibrium conditions of each of these parts separately.
Section AB can be oriented in any way, but a cross section perpendicular to the longitudinal axis of the rod turns out to be more convenient for further discussion.
Let us introduce the following notation:
main vectors and main moments of external and internal forces applied to the left cut-off part. Taking into account the introduced notation, the equilibrium conditions of this body can be written as:
0, + =0 (2.1.1)
Similar expressions can be compiled for the right cut off part of the rod. After simple transformations you can get:
=- , =- (2.1.1)
which can be interpreted as a consequence of the well-known law of mechanics: an action is always accompanied by an equal and opposite reaction.
In the case of solving the problem of dynamic action on a rod, one can turn to the well-known d’Alembert principle, according to which inertial forces are added to external forces, which again reduces the problem to equilibrium equations. Therefore, the section method procedure remains
The values and do not depend on the orientation of the section AB (see Fig. 2.1.5). However, in practical calculations it seems most convenient to use a cross section. In this case, the normal to the section coincides with the longitudinal axis of the rod. Further, the main vector and the main moment of internal forces are usually presented in the form of their projections onto orthogonal coordinate axes, with one of the axes (for example, the x axis) aligned with the mentioned normal, see Fig. 2.1.6.
Figure 2.1.6
Let us expand the vectors , , , along the coordinate axes, Fig. 2.1.6, a-d. The components of the main vector and the main moment have generally accepted names. The force N x normal to the section plane is called the normal (longitudinal) force, and Q x and Q y are called transverse (cutting) forces. Moments about the axes at And z, i.e. M y and M z will be bending and the moment relative to the longitudinal axis X, i.e. M x - torque.
The components of the main moment of internal forces in the resistance of materials are most often displayed as shown in Fig. 2.1.6, d and f.
Vector equilibrium equations can be represented as a projection onto the coordinate axes:
Thus, each component of the main vector for the main moment of internal forces is calculated as the sum of the projections of all external forces onto the corresponding axis or as the sum of the moments of all external forces relative to this axis (taking into account the accepted sign rule), located on one side of the section.
The projection of a vector onto the coordinate axis, being a scalar quantity, can be either positive or negative. This depends on whether the direction of the projection coincides with the positive or negative direction of the axis, respectively. For internal forces, this rule is observed only for the case when the normal X is external, as was the case for the left cut off part in Fig. 2.1.6. In a situation where normal X is internal, see the right cut off part in Fig. 2.1.6, the sign of the internal force is taken positive when its direction coincides with the negative direction of the axis. In Fig. 2.1.6 all projections of internal forces N x , Q x , Q y , M x , M y and M z (both those related to the left and those related to the right cut-off parts) are depicted as positive.
Deformation, strength and rigidity. Strength of materials is a part of mechanics that deals with the design of structural elements for strength, stiffness and stability.
Strength of materials is based on knowledge of theoretical mechanics. But if the object of theoretical mechanics is an absolutely rigid body, then the resistance of materials considers deformable solids.
In practice, real parts of machines and structures are exposed to various types of forces. Under the influence of these forces, deformation of bodies occurs, i.e. change in the relative arrangement of material particles. If the forces are strong enough, destruction of the body is possible.
The ability of a body to absorb loads without destruction and large deformations is called strength and rigidity, respectively.
Some equilibrium states of bodies and structures turn out to be unstable, i.e. those in which minor mechanical impacts, usually of a random nature, can lead to significant deviations from these conditions. If the deviations are also small, then such equilibrium states are called stable.
External forces. External forces acting on a structure include active forces (loads) and reactions of external connections. There are several types of loads.
Concentrated force applied at a point. It is introduced instead of real forces acting on a small area of the surface of a structural element, the dimensions of which can be neglected.
Distributed forces. For example, liquid pressure forces on the bottom of a vessel refer to loads distributed over the surface and are measured in units, and weight forces refer to loads distributed over the volume and measured in units. In some cases, a load is introduced distributed along the line, the intensity of which is measured in
One of the load options is a concentrated moment (a pair of forces).
Internal forces in the rod. The most common structural element is the rod, so in the strength of materials it is given the main attention.
The longitudinal axis and cross section are the main geometric elements of the rod. It is assumed that the cross sections of the rod
perpendicular to the longitudinal axis, and the longitudinal axis passes through the centers of gravity of the cross sections.
The internal forces of a rod are the interaction forces between its individual parts that arise under the influence of external forces (it is assumed that in the absence of external forces, the internal forces are equal to zero).
Let us consider a rod that is in equilibrium under the action of some system of external forces (Fig. 1, a). Let's mentally draw an arbitrary cross section that divides the rod into two parts L and P. The right part P of the rod from the left part L is acted upon by a system of forces distributed over the surface of the cross section - internal forces in relation to the rod as a whole. This system of forces can be reduced to the main vector and the main moment M, taking the center of gravity of the section - point O - as the center of reduction.
Internal power factors. Let's choose a coordinate system, placing the x, y axes in the cross section, and the axis perpendicular to it, and decompose M into components along these axes: (Fig. 1, b).
These six quantities are called the internal force factors of the rod (or internal forces) in the section under consideration. Each of these forces has its own name, corresponding to its direction or a certain type of deformation of the rod, which is caused by this force. The forces are called transverse (shear) forces, and are called normal (longitudinal) force. The moments are called bending moments and torque.
