From school course mathematicians know that a quadratic trinomial is understood as an expression of the form
ax 2 + bx + c, where a ≠ 0.
The roots of this trinomial are calculated using the formula: X 1.2 = (-b ± √D) / (2a), where D = b 2 – 4ac.
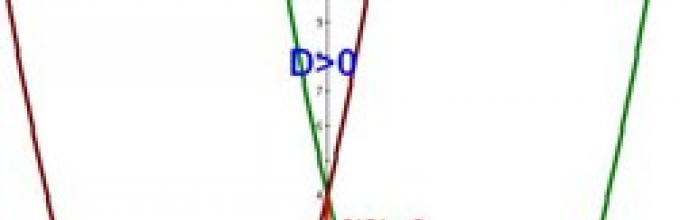
D is called discriminant. It is of utmost importance for solving problems on this topic, since it determines the number of roots of a trinomial.
There are two of them - if D > 0, one - if D = 0(sometimes they say two are identical, i.e. x 1 = x 2 = -b/(2a)), and if D< 0, то действительных корней нет.
A function of the form (*) y = ax 2 + bx + c, where a ≠ 0 is called quadratic. Its graph is a parabola, the branches of which are directed upward if a > 0 and downward if a< 0. Корни соответствующего квадратного трехчлена есть нули функции, т.е. точки пересечения параболы с осью ОХ. The point of intersection of the parabola with the axis OU is c. It is easy to determine the coordinates of the vertex of the parabola (m ;n).
m = (x 1 + x 2)/2 or (**) m = -b/(2a).
n can be calculated by substituting the value of m for x in the formula
y = ax 2 + bx + c, or use the formula y = -D/(4a).
If in a quadratic trinomial we isolate perfect square, then m and n will be present in the record in explicit form: (***) y = a(x – m) 2 + n.
Almost all of it is presented here. reference material necessary to solve problems on the stated topic. Let's look at some examples of tasks.
Example 1.
For what values of a does the vertex of the parabola y = (x – 13a) 2 – a 2 + 6a + 16 lie in the second quarter of the coordinate plane?
Solution.
The quadratic function is written in the form of a distinguished perfect square (***).
Then it is clear that m = 13a and n = -a 2 + 6a + 16. For a vertex with coordinates (m; n) to lie in the second quarter it is necessary that m< 0, n >0. Conditions must be satisfied simultaneously. Therefore, we solve the system of inequalities:
(13a< 0,
(-a 2 + 6a + 16 > 0
From the first inequality we have a< 0. Второе решаем методом интервалов или путем графического представления. Не зависимо от способа, получаем его решение: а Є (-2: 8). Решение системы неравенств есть пересечение (общая часть) полученных решений:а Є (-2: 0).
Answer: for all a Є(-2: 0) or for -2< a < 0.
Example 2.
At what values of parameter a highest value function y = ax 2 – 2x + 7a equals 6?
Solution.
The quadratic function will have the greatest value only if the branches of the parabola are directed downwards (i.e. a< 0) и достигнет его функция в вершине параболы. Иначе говоря, y max = n = 6 достигается при х = m. Исходя из формулы (**), имеем
m = 2/2a. D = 4 – 28a 2 .
Then n = (28a 2 – 4)/4a = (7a 2 – 1)/a = 6; or 7a 2 – 1 = 6a.
Having solved the resulting equation, we have a = 1 or a = -1/7. But a = 1 do not satisfy the first condition.
Answer: at a = -1/7.
Example 3.
Find the number of integer values of the parameter a for which the equation
a) |x 2 – 8x + 7| = a 2 ; b) |x 2 – 6|x| – 16| = a 2 + 9 has 4 roots.
Solution.
a) Here the shortest way to solve is graphical. The plan is:
1. Build a graph of the function y = x 2 – 8x + 7 (parabola).
2. Then y = |x 2 – 8x + 7| (display the bottom of the graph relative to OX).
The further course of the solution is obvious from the figure. The straight line will intersect the graph at four points if 0< a 2 < 9 или a = ±1; a = ±2.
Answer: 4.
b) The solution to this example is carried out according to the same scheme. The only difference is that when plotting the function y = |x 2 – 6|x| – 16| you will have to make two displays: relative to the OX of the bottom part of the graph and relative to the OU - on the right. If you plot the graph correctly, you will easily find 7 solutions:
a = 0; a = ±1; a = ±2; a = ±4;
Example 4.
For what values of a does the graph of the quadratic trinomial y = ax 2 + (a – 3)x + a lie above the x-axis?
Solution.
Let us carry out the following reasoning. The graph of a quadratic trinomial will lie above the OX axis only if the branches of the parabola are directed upward, i.e.
a > 0 (*), and the parabola does not intersect the OX axis, i.e. D< 0 или
(a – 3) 2 – 4a 2< 0 → (-a – 3)(3a – 3) < 0 → (a + 3)(3a – 3) >0 → a Є (-∞; -3) or (1; ∞). Taking into account condition (*), we obtain a Є (1; ∞).
Answer: a Є (1; ∞).
Example 5.
For what values of a does the graph of the quadratic trinomial y = ax 2 + (a – 3)x + a have two common points with the positive part of the OX axis?
Solution.
Let's look at the conditions for the coefficients: (see figure below)

1. We get two points of intersection with the OX axis if
D > 0 → (a – 3)2 – 4a2 > 0
2. The points will be on the same side of zero if the branches are directed upward and f(0) = a > 0 or in the case when the branches are directed downward and f(0) = a< 0
3. Both roots will be positive if the x-coordinate of the vertex is positive, i.e. m = -(a – 3)/(2a) > 0.
Based on the above, our conditions will be reduced to solving two systems:
First system:
((a – 3) 2 – 4a 2 > 0,
(a > 0,
(-(a – 3)/(2a) > 0
Simplifying, we get:
((3a – 3)(a + 3)< 0,
(a > 0,
((a – 3)< 0
(a Є (-3; 1),
(a Є (0; ∞),
(a Є (-∞; 3)
And general solution systems a Є(0; 1).
Second system:
((a – 3) 2 – 4a 2 > 0,
(a< 0,
(-(a – 3)/(2a) > 0
Simplifying, we get:
((3a – 3)(a + 3)< 0,
(a< 0,
((a – 3) > 0
Solutions to each of the inequalities:
(a Є (-3; 1)
(a Є (-∞; 0)
(a Є (3; ∞)
and the system has no solutions
Thus our the parabola has two common points with the positive direction of the OX axis if the parameter a Є (0; 1).
Example 6.
At what values of a are the roots of the equation 4a 2 x 2 – 8ax + 4 – 9a 2 = 0 greater than 3?
Consider the graph of the quadratic trinomial y = 4a 2 x 2 – 8ax + 4 – 9a 2.
We will build a plan for solving this task based on the previous example.

1. We obtain two points of intersection with the OX axis if D > 0 and a ≠ 0.
2. The branches here are always directed only upwards
(for a ≠ 0; 4a 2 > 0).
3. The points will be on the same side of 3 if f(3) > 0.
(36a 2 – 24a + 4 – 9a 2 > 0).
4. Both roots will be greater (to the right) of three if the x-coordinate of the vertex is greater (to the right) of three, i.e. m = 8a/(8a 2) > 3.
If you use these conditions correctly, then answer get this: a Є(0;2/9). Check it out.
I hope it now becomes clear to the reader how important it is to be able to clearly see the properties of a parabola when solving problems of this type.
Still have questions? Don't know how to solve quadratic equations?
To get help from a tutor, register.
The first lesson is free!
website, when copying material in full or in part, a link to the source is required.
Definition
Parabola called a graph quadratic function$y = ax^(2) + bx + c$, where $a \neq 0$.
Graph of the function $y = x^2$.
To schematically plot the graph of the function $y = x^2$, we will find several points that satisfy this equality. For convenience, we write down the coordinates of these points in the form of a table:
Graph of the function $y = ax^2$.
If the coefficient $a > 0$, then the graph $y = ax^2$ is obtained from the graph $y = x^2$ either by vertical stretching (for $a > 1$) or compression to the $x$ axis (for $0< a < 1$). Изобразим для примера графики $y = 2x^2$ и $y = \dfrac{x^2}{2}$:
| $y = 2x^2$ | $y = \dfrac(x^2)(2)$ |
|
|
If $a< 0$, то график функции $y = ax^2$ можно получить из графика $y = |a|x^2$, отразив его симметрично относительно оси $x$. Построим графики функций $y = - x^2$, $y = -2x^2$ и $y = - \dfrac{x^2}{2}$:
| $y = - x^2$ | $y = -2x^2$ | $y = - \dfrac(x^2)(2)$ |
|
|
|
Graph of a quadratic function.
To plot the function $y = ax^2 + bx + c$, you need to isolate a complete square from the quadratic trinomial $ax^2 + bx + c$, that is, represent it in the form $a(x - x_0)^2 + y_0$ . The graph of the function $y = a(x - x_0)^2 + y_0$ is obtained from the corresponding graph $y = ax^2$ by shifting by $x_0$ along the $x$ axis, and by $y_0$ along the $y$ axis. As a result, point $(0;0)$ will move to point $(x_0;y_0)$.
Definition
The top the parabola $y = a(x - x_0)^2 + y_0$ is the point with coordinates $(x_0;y_0)$.
Let's construct a parabola $y = 2x^2 - 4x - 6$. Selecting the perfect square, we get $y = 2(x - 1)^2 - 8$.
| Let's plot $y = 2x^2$ | Let's move it to the right by 1 | And down by 8 |
|
|
|
The result is a parabola with its vertex at point $(1;-8)$.
The graph of the quadratic function $y = ax^2 + bx + c$ intersects the $y$ axis at the point $(0; c)$ and the $x$ axis at the points $(x_(1,2);0)$, where $ x_(1,2)$ are the roots of the quadratic equation $ax^2 + bx + c = 0$ (and if the equation has no roots, then the corresponding parabola does not intersect the $x$ axis).
For example, the parabola $y = 2x^2 - 4x - 6$ intersects the axes at the points $(0; -6)$, $(-1; 0)$ and $(3; 0)$.
Graph of a quadratic trinomial
2019-04-19
Square trinomial
We call a square trinomial the whole rational function second degree:
$y = ax^2 + bx + c$, (1)
where $a \neq 0$. Let us prove that the graph of a quadratic trinomial is a parabola obtained by parallel shifts (in directions coordinate axes) from the parabola $y = ax^2$. To do this, we present expression (1) using simple identity transformations to mind
$y = a(x + \alpha)^2 + \beta$. (2)
The corresponding transformations, written below, are known as "exact square extraction":
$y = x^2 + bx + c = a \left (x^2 + \frac(b)(a) x \right) + c = a \left (x^2 + \frac(b)(a) x + \frac (b^2)(4a^2) \right) - \frac (b^2)(4a) + c = a \left (x + \frac(b)(2a) \right)^2 - \frac (b^2 - 4ac)(4a)$. (2")
We have reduced the quadratic trinomial to form (2); at the same time
$\alpha = \frac(b)(2a), \beta = - \frac (b^2 - 4ac)(4a)$
(these expressions should not be memorized; it is more convenient to transform the trinomial (1) to the form (2) directly each time).
Now it is clear that the graph of the trinomial (1) is a parabola equal to the parabola $y = ax^2$ and obtained by shifting the parabola $y = ax^2$ in the directions of the coordinate axes by $\alpha$ and $\beta$ (taking into account the sign $\alpha$ and $\beta$) respectively. The vertex of this parabola is located at the point $(- \alpha, \beta)$, its axis is the straight line $x = - \alpha$. For $a > 0$ the vertex is lowest point parabolas, for $a
Let us now conduct a study of the quadratic trinomial, i.e., we will find out its properties depending on the numerical values of the coefficients $a, b, c$ in its expression (1).
In equality (2") we denote the value $b^2- 4ac$ by $d$:
$y = a \left (x + \frac(b)(2a) \right)^2 - \frac(d)(4a)$; (4)
$d = b^2 - 4ac$ is called the discriminant of a quadratic trinomial. The properties of the trinomial (1) (and the location of its graph) are determined by the signs of the discriminant $d$ and the leading coefficient $a$.

1) $a > 0, d 0$; since $a > 0$, then the graph is located above the vertex $O^( \prime)$; it lies in the upper half-plane ($y > 0$ - Fig. a.).
2) $a
3) $a > 0, d > 0$. The vertex $O^( \prime)$ lies below the $Ox$ axis, the parabola intersects the $Ox$ axis at two points $x_1, x_2$ (Fig. c.).
4) $a 0$. The vertex $O^( \prime)$ lies above the $Ox$ axis, the parabola again intersects the $Ox$ axis at two points $x_1, x_2$ (Fig. d).
5) $a > 0, d = 0$. The vertex lies on the $Ox$ axis itself, the parabola is located in the upper half-plane (Fig. e).
6) $a
Conclusions. If $d 0$), or lower (if $a
If $d > 0$, then the function is alternating (the graph partly lies below and partly above the $Ox$ axis). A square trinomial with $d > 0$ has two roots (zeros) $x_1, x_2$. For $a > 0$ it is negative in the interval between the roots (Fig. c) and positive outside this interval. At $a
Lesson: How to construct a parabola or quadratic function?
THEORETICAL PART
A parabola is a graph of a function described by the formula ax 2 +bx+c=0.
To construct a parabola you need to follow simple algorithm actions:
1) Parabola formula y=ax 2 +bx+c,
If a>0 then the branches of the parabola are directed up,
otherwise the branches of the parabola are directed down.
Free member c this point intersects the parabola with the OY axis;
2), it is found using the formula x=(-b)/2a, we substitute the found x into the parabola equation and find y;
3)Function zeros or, in other words, the points of intersection of the parabola with the OX axis, they are also called the roots of the equation. To find the roots we equate the equation to 0 ax 2 +bx+c=0;
Types of equations:
a) Complete quadratic equation looks like ax 2 +bx+c=0 and is solved by the discriminant;
b) Incomplete quadratic equation of the form ax 2 +bx=0. To solve it, you need to take x out of brackets, then equate each factor to 0:
ax 2 +bx=0,
x(ax+b)=0,
x=0 and ax+b=0;
c) Incomplete quadratic equation of the form ax 2 +c=0. To solve it, you need to move the unknowns to one side, and the knowns to the other. x =±√(c/a);
4) Find several additional points to construct the function.
PRACTICAL PART
And so now, using an example, we will analyze everything step by step:
Example #1:
y=x 2 +4x+3
c=3 means the parabola intersects OY at the point x=0 y=3. The branches of the parabola look up since a=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 vertex is at point (-2;-1)
Let's find the roots of the equation x 2 +4x+3=0
Using the discriminant we find the roots
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Let's take several arbitrary points that are located near the vertex x = -2
x -4 -3 -1 0
y 3 0 0 3
Substitute instead of x into the equation y=x 2 +4x+3 values
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
It can be seen from the function values that the parabola is symmetrical with respect to the straight line x = -2
Example #2:
y=-x 2 +4x
c=0 means the parabola intersects OY at the point x=0 y=0. The branches of the parabola look down since a=-1 -1 Let's find the roots of the equation -x 2 +4x=0
Incomplete quadratic equation of the form ax 2 +bx=0. To solve it, you need to take x out of brackets, then equate each factor to 0.
x(-x+4)=0, x=0 and x=4.
Let's take several arbitrary points that are located near the vertex x=2
x 0 1 3 4
y 0 3 3 0
Substitute instead of x into the equation y=-x 2 +4x values
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
It can be seen from the function values that the parabola is symmetrical with respect to the straight line x = 2
Example No. 3
y=x 2 -4
c=4 means the parabola intersects OY at the point x=0 y=4. The branches of the parabola look up since a=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 the vertex is at point (0;-4 )
Let's find the roots of the equation x 2 -4=0
Incomplete quadratic equation of the form ax 2 +c=0. To solve it, you need to move the unknowns to one side, and the knowns to the other. x =±√(c/a)
x 2 =4
x 1 =2
x 2 =-2
Let's take several arbitrary points that are located near the vertex x=0
x -2 -1 1 2
y 0 -3 -3 0
Substitute instead of x into the equation y= x 2 -4 values
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
It can be seen from the function values that the parabola is symmetrical about the straight line x = 0
Subscribe to the channel on YOUTUBE to keep abreast of all the new products and prepare with us for exams.
Defined by the formula $a((x)^(2))+bx+c$ $(a\ne 0).$ The numbers $a, b$ and $c$ are the coefficients of a quadratic trinomial, they are usually called: a - the leading one, b - second or average coefficient, c - free member. A function of the form y = ax 2 + bx + c is called a quadratic function.
All of these parabolas have their vertex at the origin; for a > 0 this is the lowest point of the graph ( smallest value functions), and for a< 0, наоборот, highest point(highest value of the function). The Oy axis is the axis of symmetry of each of these parabolas.
As can be seen, for a > 0 the parabola is directed upward, for a< 0 - вниз.
There is a simple and convenient graphic method, which allows you to construct any number of points of the parabola y = ax 2 without calculations, if a point of the parabola other than the vertex is known. Let the point M(x 0 , y 0) lie on the parabola y = ax 2 (Fig. 2). If we want to construct n additional n points between points O and M, then we divide the segment ON of the abscissa axis by n + 1 equal parts and at the division points we draw perpendiculars to the Ox axis. We divide the segment NM into the same number of equal parts and connect the division points with rays to the origin of coordinates. The required points of the parabola lie at the intersection of perpendiculars and rays with the same numbers (in Fig. 2 the number of division points is 9).
The graph of the function y =ax 2 + bx + c differs from the graph y = ax 2 only in its position and can be obtained simply by moving the curve on the drawing. This follows from the representation of the quadratic trinomial in the form
from which it is easy to conclude that the graph of the function y = ax 2 + bx + c is a parabola y = ax 2, the vertex of which is moved to the point
and its axis of symmetry remained parallel to the Oy axis (Fig. 3). From the resulting expression for a quadratic trinomial, all its basic properties easily follow. The expression D = b 2 − 4ac is called the discriminant of the quadratic trinomial ax 2 + bx + c and the discriminant of the associated quadratic equation ax 2 + bx + c = 0. The sign of the discriminant determines whether the graph of the quadratic trinomial intersects the x-axis or lies on the same side from her. Namely, if D< 0, то парабола не имеет common points with the Ox axis, in this case: if a > 0, then the parabola lies above the Ox axis, and if a< 0, то ниже этой оси (рис. 4). В случае D >0 the graph of a quadratic trinomial intersects the x-axis at two points x 1 and x 2, which are the roots of the quadratic equation ax 2 + bx + c = 0 and are equal, respectively
At D = 0 the parabola touches the Ox axis at the point
The properties of the quadratic trinomial form the basis for solving quadratic inequalities. Let's explain this with an example. Suppose we need to find all solutions to the inequality 3x 2 - 2x - 1< 0. Найдем дискриминант квадратного трехчлена, стоящего в левой части неравенства: D = 16. Так как D >0, then the corresponding quadratic equation 3x 2 − 2x − 1 = 0 has two different roots, they are determined by the formulas given earlier:
x 1 = −1/3 and x 2 = 1.
In the quadratic trinomial under consideration, a = 3 > 0, which means that the branches of its graph are directed upward and the values of the quadratic trinomial are negative only in the interval between the roots. So, all solutions to the inequality satisfy the condition
−1/3 < x < 1.
TO quadratic inequalities various inequalities can be reduced by the same substitutions as various equations reduce to square.