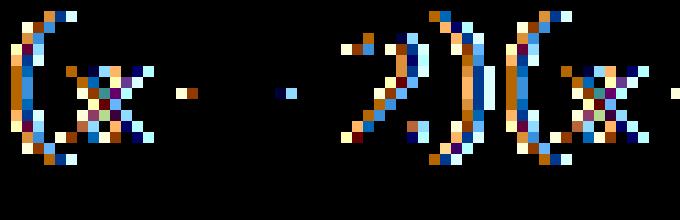It is a square, and it consists of three terms (). So it turns out - a square trinomial.
Examples Not square trinomials:
\(x^3-3x^2-5x+6\) - cubic quadrinomial
\(2x+1\) - linear binomial
Square root of the trinomial:
Example:
The trinomial \(x^2-2x+1\) has a root \(1\), because \(1^2-2 1+1=0\)
The trinomial \(x^2+2x-3\) has roots \(1\) and \(-3\), because \(1^2+2-3=0\) and \((-3)^ 2-6-3=9-9=0\)
For example: if you need to find roots for the quadratic trinomial \(x^2-2x+1\), we equate it to zero and solve the equation \(x^2-2x+1=0\).
\(D=4-4\cdot1=0\)
\(x=\frac(2-0)(2)=\frac(2)(2)=1\)
Ready. The root is \(1\).
Decomposition of a quadratic trinomial into:
The square trinomial \(ax^2+bx+c\) can be expanded as \(a(x-x_1)(x-x_2)\) if the equations \(ax^2+bx+c=0\) are greater than zero \ (x_1\) and \(x_2\) are roots of the same equation).
For example, consider the trinomial \(3x^2+13x-10\).
U quadratic equation\(3x^2+13x-10=0\) discriminant is 289 (greater than zero), and the roots are \(-5\) and \(\frac(2)(3)\). Therefore \(3x^2+13x-10=3(x+5)(x-\frac(2)(3))\). It is easy to verify the correctness of this statement - if we , then we will obtain the original trinomial.
The square trinomial \(ax^2+bx+c\) can be represented as \(a(x-x_1)^2\) if the discriminant of the equation \(ax^2+bx+c=0\) is zero.
For example, consider the trinomial \(x^2+6x+9\).The quadratic equation \(x^2+6x+9=0\) has a discriminant equal to \(0\) and a unique root equal to \(-3\). This means \(x^2+6x+9=(x+3)^2\) (here the coefficient is \(a=1\), so it is not written before the bracket - there is no need). Please note that the same conversion can be done by .
The square trinomial \(ax^2+bx+c\) is not factorized if the discriminant of the equation \(ax^2+bx+c=0\) is less than zero.
For example, the trinomials \(x^2+x+4\) and \(-5x^2+2x-1\) have a discriminant less than zero. Therefore, it is impossible to factor them.
Example
. Factor \(2x^2-11x+12\).
Solution
:
Let's find the roots of the quadratic equation \(2x^2-11x+12=0\)
\(D=11^2-4 \cdot 2 \cdot 12=121-96=25>0\)
\(x_1=\frac(11-5)(4)=1.5;\) \(x_2=\frac(11+5)(4)=4.\)
So, \(2x^2-11x+12=2(x-1.5)(x-4)\)
Answer
: \(2(x-1.5)(x-4)\)
The resulting answer may be written differently: \((2x-3)(x-4)\).
Example
. (Assignment from the OGE) Square trinomial factorized \(5x^2+33x+40=5(x++ 5)(x-a)\). Find \(a\).
Solution:
\(5x^2+33x+40=0\)
\(D=33^2-4 \cdot 5 \cdot 40=1089-800=289=17^2\)
\(x_1=\frac(-33-17)(10)=-5\)
\(x_2=\frac(-33+17)(10)=-1.6\)
\(5x^2+33x+40=5(x+5)(x+1.6)\)
Answer
: \(-1,6\)
The square trinomial can be factored as follows:
A x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2)
where a is a number, a coefficient before the leading coefficient,
x – variable (i.e. letter),
x 1 and x 2 are numbers, roots of the quadratic equation a x 2 + b x + c = 0, which are found through the discriminant.
If a quadratic equation has only one root, then the expansion looks like this:
a x 2 + b x + c = a ⋅ (x − x 0) 2
Examples of factoring a quadratic trinomial:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = (− 1) ⋅ (x − (− 1)) (x − 7) = − (x + 1) (x − 7) = (x + 1) (7 − x)
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = (− 1) ⋅ (x − 2) 2 = − (x − 2) 2
If the quadratic trinomial is incomplete (b = 0 or c = 0), then it can be factorized in the following ways:
- c = 0 ⇒ a x 2 + b x = x (a x + b)
- b = 0 ⇒ apply the abbreviated multiplication formula for the difference of squares.
Tasks for independent solution
No. 1. The square trinomial is factored: x 2 + 6 x − 27 = (x + 9) (x − a) . Find a.
Solution:
First you need to equate the quadratic trinomial to zero to find x 1 and x 2.
x 2 + 6 x − 27 = 0
a = 1, b = 6, c = − 27
D = b 2 − 4 a c = 6 2 − 4 ⋅ 1 ⋅ (− 27) = 36 + 108 = 144
D > 0 means there will be two different roots.
x 1,2 = − b ± D 2 a = − 6 ± 144 2 ⋅ 1 = [ − 6 + 12 2 = 6 2 = 3 − 6 − 12 2 = − 18 2 = − 9
Knowing the roots, we factorize the quadratic trinomial:
x 2 + 6 x − 27 = (x − (− 9)) (x − 3) = (x + 9) (x − 3)
No. 2. The equation x 2 + p x + q = 0 has roots − 5; 7. Find q.
Solution:
1 way:(you need to know how to factor a quadratic trinomial)
If x 1 and x 2 are the roots of the square trinomial a x 2 + b x + c, then it can be factorized as follows: a x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2) .
Since in a given quadratic trinomial the leading coefficient (the factor in front of x 2) is equal to one, the expansion will be as follows:
x 2 + p x + q = (x − x 1) (x − x 2) = (x − (− 5)) (x − 7) = (x + 5) (x − 7) = x 2 − 7 x + 5 x − 35 = x 2 − 2 x − 35
x 2 + p x + q = x 2 − 2 x − 35 ⇒ p = − 2, q = − 35
Method 2: (you need to know Vieta's theorem)
Vieta's theorem:
The sum of the roots of the reduced quadratic trinomial x 2 + p x + q is equal to its second coefficient p with the opposite sign, and the product is free member q.
( x 1 + x 2 = − p x 1 ⋅ x 2 = q
q = x 1 ⋅ x 2 = (− 5) ⋅ 7 = − 35.
First of all, let's point out some common names. Let's consider polynomials that contain only one letter, for example, the letter x. Then the simplest is a polynomial in which there are two terms, and one of them contains the letter x to the first degree, and the other does not have the letter x at all, for example, 3x – 5 or 15 – 7x or 8z + 7 (here instead of letter x is taken letter z), etc. Such polynomials are called linear binomials .
3x² – 5x + 7 or x² + 2x – 1
or 5y² + 7y + 8 or z² – 5z – 2, etc.
Such polynomials are called square trinomials.
Then, we can form a cubic quadrinomial, for example:
x³ + 2x² – x + 1 or 3x³ – 5x² – 2x – 3 etc.,
polynomial of the fourth degree, for example:
x 4 – 2x³ – 3x² + 4x – 5, etc.
It is possible to denote the coefficients at x, at x², at x³, etc. also by letters, for example, by the letters a, b, c, etc. Then we get:
1) general view linear relative to x binomial ax + b,
2) general form of the quadratic trinomial (relative to x): ax² + bx + c,
3) general form of the cubic trinomial (relative to x): ax³ + bx² + cx + d, etc.
By replacing the letters a, b, c, d... in these formulas with different numbers, we get all kinds of linear binomials, square trinomials, etc. For example, in the formula ax² + bx + c, which expresses the general form of a quadratic trinomial, we replace the letter a with the number + 3, the letter b with the number –2 and the letter with the number –1, we get the square trinomial 3x² – 2x – 1. In a particular case, it is also possible to obtain a binomial by replacing one of the letters with zero, for example, if a = +1, b = 0 and c = –3, then we get the quadratic binomial x² – 3.
You can learn to factor some quadratic trinomials fairly quickly into linear factors. We will, however, limit ourselves to considering only those quadratic trinomials that satisfy the following conditions:
1) the coefficient for the leading term (for x²) is +1,
2) you can find two integers (with signs, or two relative integers) such that their sum is equal to the coefficient of x to the first power and their product is equal to the term free of x (where there is no letter x at all).
Examples. 1. x² + 5x + 6; It’s easy to mentally find two numbers (with signs) so that their sum is equal to +5 (the coefficient of x) and so that their product = +6 (the term free of x) - these numbers are: +2 and +3 [in fact In fact, +2 + 3 = +5 and (+2) ∙ (+3) = +6]. Using these two numbers, we replace the +5x term with two terms, namely: +2x + 3x (of course, +2x + 3x = +5x); then our technical term will be artificially converted into a four-term x² + 2x + 3x + 6. Let us now apply the grouping technique to it, assigning the first two terms to one group and the last two to another:
x² + 5x + 6 = x² + 2x + 3x + 6 = x (x + 2) + 3 (x + 2) = (x + 2) (x + 3).
In the first group we took x out of the bracket and +3 in the second, we got two terms that had a common factor (x + 2), which we also took out of the bracket, and our trinomial x² + 5x + 6 decomposed into 2 linear factors: x + 2 and x + 3.
2. x² – x – 12. Here you need to find two numbers (relative) so that their sum is equal to –1 and so that their product is equal to –12. These numbers are: –4 and +3.
Check: –4 + 3 = –1; (–4) (+3) = –12. Using these numbers, we replace the term –x with two terms: –x = –4x + 3x, – we get:
x² – x – 12 = x² – 4x + 3x – 12 = x (x – 4) + 3 (x – 4) = (x – 4) (x + 3).
3. x² – 7x + 6; here the required numbers are: –6 and –1. [Check: –6 + (–1) = –7; (–6) (–1) = +6].
x² – 7x + 6 = x² – 6x – x + 6 = x (x – 6) – (x – 6) = (x – 6) (x – 1).
Here the members of the second group –x + 6 had to be enclosed in parentheses, with a minus sign in front of them.
4. x² + 8x – 48. Here you need to find two numbers so that their sum is +8 and their product is –48. Since the product must have a minus sign, then the required numbers must have different signs, since the sum of our numbers has a + sign, then absolute value there must be more positive numbers. Unfolding arithmetic number 48 by two factors (and this can be done in different ways), we get: 48 = 1 ∙ 48 = 2 ∙ 24 = 3 ∙ 16 = 4 ∙ 12 = 6 ∙ 8. From these expansions it is easy to choose the one that suits our requirements, namely : 48 = 4 ∙ 12. Then our numbers are: +12 and –4. The rest is simple:
x² + 8x – 48 = x² + 12x – 4x – 48 = x (x + 12) – 4 (x + 12) = (x + 12) (x – 4).
5. x² + 7x – 12. Here you need to find 2 numbers so that their sum is +7 and product = –12; 12 = 1 ∙ 12 = 2 ∙ 6 = 3 ∙ 4. Apparently, suitable numbers would be 3 and 4, but they must be taken with different signs so that their product is equal to –12, and then their sum in no case may be +7 [–3 + (+4) = +1, +3 + (–4) = –1]. Other factorizations also do not give the required numbers; Therefore, we come to the conclusion that we are not yet able to decompose these quadratic trinomials into linear factors, since our technique is not applicable to it (it does not satisfy the second of the conditions that were established at the beginning).
In this lesson we will learn how to factor quadratic trinomials into linear factors. To do this, we need to remember Vieta’s theorem and its converse. This skill will help us quickly and conveniently expand quadratic trinomials into linear factors, and will also simplify the reduction of fractions consisting of expressions.
So let's go back to the quadratic equation, where .
What we have on the left side is called a quadratic trinomial.
The theorem is true: If are the roots of a quadratic trinomial, then the identity holds
Where is the leading coefficient, are the roots of the equation.
So, we have a quadratic equation - a quadratic trinomial, where the roots of the quadratic equation are also called the roots of the quadratic trinomial. Therefore, if we have the roots of a square trinomial, then this trinomial is decomposed into linear factors.
Proof:
Proof this fact is performed using Vieta's theorem, which we discussed in previous lessons.
Let's remember what Vieta's theorem tells us:
If are the roots of a quadratic trinomial for which , then .
The following statement follows from this theorem:
We see that, according to Vieta’s theorem, i.e., by substituting these values into the formula above, we obtain the following expression
Q.E.D.
Recall that we proved the theorem that if are the roots of a square trinomial, then the expansion is valid.
Now let's remember an example of a quadratic equation, to which we selected roots using Vieta's theorem. From this fact we can obtain the following equality thanks to the proven theorem:
Now let's check the correctness of this fact by simply opening the brackets:
We see that we factored correctly, and any trinomial, if it has roots, can be factorized according to this theorem into linear factors according to the formula
However, let's check whether such factorization is possible for any equation:
Take, for example, the equation . First, let's check the discriminant sign
And we remember that in order to fulfill the theorem we learned, D must be greater than 0, so in this case, factorization according to the theorem we learned is impossible.
Therefore, we formulate a new theorem: if a square trinomial has no roots, then it cannot be decomposed into linear factors.
So, we have looked at Vieta's theorem, the possibility of decomposing a quadratic trinomial into linear factors, and now we will solve several problems.
Task No. 1
In this group we will actually solve the problem inverse to the one posed. We had an equation, and we found its roots by factoring it. Here we will do the opposite. Let's say we have the roots of a quadratic equation
The inverse problem is this: write a quadratic equation using its roots.
There are 2 ways to solve this problem.
Since are the roots of the equation, then ![]() is a quadratic equation whose roots are given numbers. Now let's open the brackets and check:
is a quadratic equation whose roots are given numbers. Now let's open the brackets and check:
![]()
This was the first way we created a quadratic equation with given roots, which does not have any other roots, since any quadratic equation has at most two roots.
This method involves using converse theorem Vieta.
If are the roots of the equation, then they satisfy the condition that .
For the reduced quadratic equation ![]() , , i.e. in this case, and .
, , i.e. in this case, and .
Thus, we have created a quadratic equation that has the given roots.
Task No. 2
It is necessary to reduce the fraction.
We have a trinomial in the numerator and a trinomial in the denominator, and the trinomials can either be factorized or not. If both the numerator and the denominator are factored, then among them there may be equal factors that can be reduced.
First of all, you need to factor the numerator.
First, you need to check whether this equation can be factorized, let’s find the discriminant. Since , the sign depends on the product (must be less than 0), in in this example, i.e. given equation has roots.
![]()
To solve, we use Vieta’s theorem:

In this case, since we are dealing with roots, it will be quite difficult to simply select the roots. But we see that the coefficients are balanced, that is, if we assume that , and substitute this value into the equation, we get the following system: , i.e. 5-5=0. Thus, we have selected one of the roots of this quadratic equation.
We will look for the second root by substituting what is already known into the system of equations, for example, , i.e. .
Thus, we have found both roots of the quadratic equation and can substitute their values into the original equation to factor it:
![]()
Let's remember the original problem, we needed to reduce the fraction .
Let's try to solve the problem by substituting .
It is necessary not to forget that in this case the denominator cannot be equal to 0, i.e. , .
If these conditions are met, then we have reduced the original fraction to the form .
Problem No. 3 (task with a parameter)
At what values of the parameter is the sum of the roots of the quadratic equation
If the roots of this equation exist, then ![]() , question: when.
, question: when.
SQUARE TRIPLE III
§ 54. Decomposition of a quadratic trinomial into linear factors
In this section we will consider the following question: in what case is the quadratic trinomial ax 2 + bx + c can be represented as a product
(a 1 x+b 1) (a 2 x+b 2)
two linear relative X multipliers with real coefficients a 1 , b 1 , a 2 , b 2 (a 1 =/=0, a 2 =/=0) ?
1. Suppose that the given quadratic trinomial ax 2 + bx + c let's represent it in the form
ax 2 + bx + c = (a 1 x+b 1) (a 2 x+b 2). (1)
The right-hand side of formula (1) vanishes when X = - b 1 / a 1 and X = - b 2 / a 2 (a 1 and a 2 are not equal to zero by condition). But in this case the numbers are b 1 / a 1 and - b 2 / a 2 are the roots of the equation
ax 2 + bx + c = 0.
Therefore, the discriminant of the quadratic trinomial ax 2 + bx + c must be non-negative.
2. Conversely, suppose that the discriminant D = b 2 - 4ac quadratic trinomial ax 2 + bx + c non-negative. Then this trinomial has real roots x 1 and x 2. Using Vieta's theorem, we obtain:
ax 2 + bx + c =A (x 2 + b / a X + c / a ) = A [x 2 - (x 1 + x 2) X + x 1 x 2 ] =
= A [(x 2 - x 1 x ) - (x 2 x - x 1 x 2)] = A [X (X - x 1) - x 2 (X - x 1) =
=a (X - x 1)(X - x 2).
ax 2 + bx + c = a (X - x 1)(X - x 2), (2)
Where x 1 and x 2 - roots of the trinomial ax 2 + bx + c . Coefficient A can be attributed to either of two linear factors, for example,
a (X - x 1)(X - x 2) = (ah - ax 1)(X - x 2).
But this means that in the case under consideration the square trinomial ax 2 + bx + c Let us present it as a product of two linear factors with real coefficients.
Combining the results obtained in paragraphs 1 and 2, we arrive at the following theorem.
Theorem. Square trinomial ax 2 + bx + c then and only then can be represented as a product of two linear factors with real coefficients,
ax 2 + bx + c = (ah - ax 1)(X - x 2),
when the discriminant of this quadratic trinomial is non-negative (that is, when this trinomial has real roots).
Example 1. Linear factorize 6 x 2 - X -1.
The roots of this quadratic trinomial are equal x 1 = 1/2 and x 2 = - 1 / 3 .
Therefore, according to formula (2)
6x 2 - X -1 = 6 (X - 1 / 2)(X + 1 / 3) = (2X - 1) (3x + 1).
Example 2. Linear factorization x 2 + X + 1. The discriminant of this quadratic trinomial is negative:
D = 1 2 - 4 1 1 = - 3< 0.
Therefore, this quadratic trinomial cannot be expanded into linear factors with real coefficients.
Exercises
Factor the following expressions into linear factors (No. 403 - 406):
403. 6x 2 - 7X + 2. 405. x 2 - X + 1.
404. 2x 2 - 7Oh + 6A 2 . 406. x 2 - 3Oh + 2A 2 - ab - b 2 .
Reduce fractions (No. 407, 408):
Solve equations: