Երբ ես դպրոց էի սովորում, մեր ֆիզիկայի ուսուցիչը՝ Բադեր անունով, մի անգամ դասից հետո ինձ կանչեց և ասաց. մի հետաքրքիր բան լսիր»։ Եվ նա ինձ մի բան ասաց, որը, իմ կարծիքով, իսկապես հետաքրքրաշարժ էր: Նույնիսկ հիմա, թեև դրանից հետո շատ ժամանակ է անցել, այն շարունակում է ինձ գրավել։ Եվ ամեն անգամ, երբ հիշում եմ ասածս, վերադառնում եմ աշխատանքի։ Եվ այս անգամ, երբ պատրաստվում էի դասախոսությանը, նորից վերլուծում էի նույն բաները։ Եվ, դասախոսությանը պատրաստվելու փոխարեն, ես նոր խնդիր ստանձնեցի. Թեման, որի մասին ես խոսում եմ նվազագույն գործողության սկզբունքը.


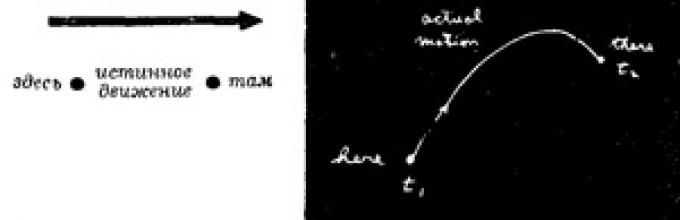
«Ահա թե ինչ ասաց ինձ իմ ուսուցիչ Բադերը այն ժամանակ. այս մասնիկը, դուրս գալով ինչ-որ տեղից, ազատորեն տեղափոխվում է ինչ-որ տեղ այլ կետ: Դու նետեցիր, ասենք, վերև, և այն վեր թռավ, հետո ընկավ։

Նրանից որոշ ժամանակ պահանջվեց մեկնարկային վայրից մինչև վերջնական տեղ ճանապարհորդելու համար: Հիմա փորձեք ինչ-որ այլ շարժում: Թող նա տեղափոխվի «այստեղից այստեղ» այլևս ոչ թե նախկինի պես, այլ այսպես.

Բայց ես դեռ հայտնվեցի ճիշտ տեղում՝ ժամանակի նույն պահին, ինչ նախկինում»։

«Եվ այսպես, - շարունակեց ուսուցիչը, - եթե հաշվարկեք կինետիկ էներգիան ժամանակի յուրաքանչյուր պահի մասնիկի ճանապարհին, հանեք նրանից պոտենցիալ էներգիան և ինտեգրեք տարբերությունը ամբողջ ժամանակի ընթացքում, երբ տեղի է ունեցել շարժումը, կտեսնեք. որ ձեր ստացած թիվը կլինի ավելին,քան մասնիկների իրական շարժման համար:

Այլ կերպ ասած, Նյուտոնի օրենքները կարող են ձևակերպվել ոչ թե F=ma, այլ հետևյալ կերպ. միջին կինետիկ էներգիան հանած միջին պոտենցիալ էներգիան հասնում է իր ամենացածր արժեքին այն հետագծի երկայնքով, որով առարկան իրականում տեղափոխվում է մի վայրից մյուսը:

Ես կփորձեմ դա ձեզ մի փոքր ավելի պարզ բացատրել:
Եթե ​​վերցնենք գրավիտացիոն դաշտը և նշանակենք մասնիկի հետագիծը x(տ), Որտեղ X- բարձրությունը գետնից բարձր (այժմ եկեք հաղթահարենք մեկ հարթություն. թող հետագիծը վազի միայն վեր ու վար, և ոչ թե կողքերը), ապա կինետիկ էներգիան կլինի y 2 մ(dx/ dt) 2, ապոտենցիալ էներգիան ժամանակի կամայական պահին հավասար կլինի mgx.


Այժմ, հետագծի երկայնքով շարժվելու մի պահ, ես վերցնում եմ կինետիկ և պոտենցիալ էներգիաների տարբերությունը և ինտեգրվում ամբողջ ժամանակի ընթացքում՝ սկզբից մինչև վերջ: Թող սկզբնական պահին t x շարժումը սկսվեց ինչ-որ բարձրության վրա և ավարտվեց այս պահին տ 2 մեկ այլ որոշակի բարձրության վրա:

Ապա ինտեգրալը հավասար է ∫ t2 t1 dt

Իրական շարժումը տեղի է ունենում որոշակի կորի երկայնքով (որպես ժամանակի ֆունկցիա այն պարաբոլա է) և հանգեցնում է որոշակի ինտեգրալ արժեքի: Բայց դու կարող ես նախքանդնելպատկերացրեք ինչ-որ այլ շարժում՝ սկզբում կտրուկ վերելք, իսկ հետո որոշ տարօրինակ տատանումներ:

Դուք կարող եք հաշվարկել պոտենցիալ և կինետիկ էներգիաների տարբերությունը այս ճանապարհով... կամ ցանկացած այլ ճանապարհով: Եվ ամենազարմանալին այն է, որ իրական ճանապարհն այն է, որով այս ինտեգրալը ամենափոքրն է։
Եկեք ստուգենք այն: Նախ, եկեք նայենք այս դեպքին. ազատ մասնիկը բացարձակապես չունի պոտենցիալ էներգիա: Այնուհետև կանոնն ասում է, որ տվյալ ժամանակում մի կետից մյուսը տեղափոխվելիս կինետիկ էներգիայի ինտեգրալը պետք է լինի ամենափոքրը։ Սա նշանակում է, որ մասնիկը պետք է շարժվի միատեսակ։ (Եվ սա ճիշտ է, ես և դու գիտենք, որ նման շարժման արագությունը հաստատուն է:) Ինչու՞ միատեսակ: Եկեք պարզենք այն: Եթե ​​այլ կերպ լիներ, ապա ժամանակ առ ժամանակ մասնիկի արագությունը կգերազանցի միջինը, իսկ երբեմն այն կլիներ դրանից ցածր, և միջին արագությունը նույնը կլիներ, քանի որ մասնիկը պետք է «այստեղից այստեղ» հասներ: համաձայնեցված ժամանակին։ Օրինակ, եթե ձեզ անհրաժեշտ է որոշակի ժամանակում տնից դպրոց հասնել ձեր մեքենայով, ապա դա կարող եք անել տարբեր ձևերով. սկզբում կարող եք խելագարի պես վարել, իսկ վերջում դանդաղեցնել արագությունը, կամ վարել նույն արագությամբ, կամ նույնիսկ կարող ես գնալ հակառակ կողմ, և միայն դրանից հետո շրջվել դեպի դպրոց և այլն: Բոլոր դեպքերում միջին արագությունը, իհարկե, պետք է լինի նույնը` տանից դպրոց հեռավորության գործակիցը բաժանված ժամանակի վրա: Բայց նույնիսկ այս միջին արագության դեպքում երբեմն շատ արագ էիր շարժվում, երբեմն էլ՝ շատ դանդաղ։ Եվ միջին քառակուսիմի բան, որը շեղվում է միջինից, ինչպես գիտենք, միշտ ավելի մեծ է միջինի քառակուսուց. Սա նշանակում է, որ շարժման արագության տատանումների ժամանակ կինետիկ էներգիայի ինտեգրալը միշտ ավելի մեծ կլինի, քան հաստատուն արագությամբ շարժվելիս։ Դուք տեսնում եք, որ ինտեգրալը կհասնի նվազագույնի, երբ արագությունը հաստատուն է (ուժերի բացակայության դեպքում): Ճիշտ ճանապարհը սա է.

Ծանրության դաշտում դեպի վեր նետված առարկան սկզբում արագ է բարձրանում, իսկ հետո ավելի ու ավելի դանդաղ։ Դա տեղի է ունենում, քանի որ այն ունի նաև պոտենցիալ էներգիա, և դրա նվազագույն արժեքը պետք է հասնի մեկ անգամէսկինետիկ և պոտենցիալ էներգիաների միջև: Քանի որ պոտենցիալ էներգիան մեծանում է, երբ դուք բարձրանում եք, ապա ավելի քիչ տարբերությունըԴա կաշխատի, եթե հնարավորինս արագ հասնեք այն բարձունքներին, որտեղ պոտենցիալ էներգիան բարձր է: Այնուհետև այս բարձր պոտենցիալը հանելով կինետիկ էներգիայից՝ հասնում ենք միջինի նվազմանը։ Այսպիսով, ճանապարհը, որը բարձրանում է և պոտենցիալ էներգիայի հաշվին լավ բացասական կտոր է մատակարարում, ավելի շահավետ է:

Դա այն ամենն էր, ինչ ինձ ասաց իմ ուսուցիչը, քանի որ նա շատ լավ ուսուցիչ էր և գիտեր, թե երբ է կանգ առնելու ժամանակը: Ես ինքս, ավաղ, այդպիսին չեմ։ Ինձ համար դժվար է ժամանակին կանգ առնելը: Եվ այսպես, իմ պատմվածքով պարզապես ձեր հետաքրքրությունը առաջացնելու փոխարեն, ես ուզում եմ ձեզ վախեցնել, ես ուզում եմ ձեզ զզվել կյանքի բարդությունից - ես կփորձեմ ապացուցել այն, ինչ ձեզ ասացի: Մաթեմատիկական խնդիրը, որը մենք կլուծենք, շատ բարդ է և եզակի։ Կա որոշակի քանակություն Ս, կանչեց գործողություն.Այն հավասար է կինետիկ էներգիայի՝ հանած ժամանակի ընթացքում ինտեգրված պոտենցիալ էներգիան.

Բայց մյուս կողմից, դուք չեք կարող շատ արագ շարժվել կամ բարձրանալ, քանի որ դրա համար չափազանց շատ կինետիկ էներգիա կպահանջվի: Դուք պետք է բավականաչափ արագ շարժվեք, որպեսզի վեր կենաք և իջնեք ձեզ հասանելի ժամանակահատվածում: Այսպիսով, դուք չպետք է փորձեք շատ բարձր թռչել, այլ պարզապես հասնեք որոշակի ողջամիտ մակարդակի: Արդյունքում պարզվում է, որ լուծումը մի տեսակ հավասարակշռություն է հնարավորինս շատ պոտենցիալ էներգիա ստանալու ցանկության և կինետիկ էներգիայի քանակը հնարավորինս նվազեցնելու ցանկության միջև. սա առավելագույն կրճատման հասնելու ցանկությունն է: կինետիկ և պոտենցիալ էներգիաների տարբերության մեջ»։

Մի մոռացեք, որ p.e. և k.e. — ժամանակի երկու գործառույթներն էլ։ Ցանկացած նոր ըմբռնելի ճանապարհի համար այս գործողությունը ստանում է իր հատուկ նշանակությունը: Մաթեմատիկական խնդիրն այն է, որ որոշվի, թե որ կորի մեջ այս թիվը փոքր է մյուսներից:

Դուք ասում եք. «Օ, սա ընդամենը առավելագույնի և նվազագույնի պարզ օրինակ է: Պետք է հաշվարկել գործողությունը, տարբերակել ու գտնել նվազագույնը»։

Բայց սպասիր։ Սովորաբար մենք ունենք որոշ փոփոխականի ֆունկցիա և պետք է գտնել արժեքը փոփոխական,որի դեպքում ֆունկցիան դառնում է ամենափոքրը կամ ամենամեծը: Ասենք՝ մեջտեղում տաքացվող ձող կա։ Ջերմությունը տարածվում է դրա վրա, և ձողի յուրաքանչյուր կետում հաստատվում է իր սեփական ջերմաստիճանը: Դուք պետք է գտնեք այն կետը, որտեղ այն ամենաբարձրն է: Բայց մենք խոսում ենք բոլորովին այլ բանի մասին. տիեզերքում գտնվող յուրաքանչյուր ուղիպատասխանում է իր թվին և պետք է գտնի այդ մեկը ճանապարհ,որի համար այս թիվը նվազագույն է: Սա մաթեմատիկայի բոլորովին այլ ոլորտ է: Սա սովորական հաշվարկ չէ, այլ փոփոխական(այդպես են նրան անվանում):

Մաթեմատիկայի այս ոլորտն ունի իր բազմաթիվ խնդիրներ: Ասենք, շրջանագիծը սովորաբար սահմանվում է որպես կետերի տեղ, որոնց հեռավորությունները տվյալ կետից նույնն են, բայց շրջանագիծը կարող է տարբեր կերպ սահմանվել. այն կորերից մեկն է: տրված երկարությունը,որն ընդգրկում է ամենամեծ տարածքը։ Նույն պարագծի ցանկացած այլ կորը շրջապատում է շրջանագծից փոքր տարածք: Այսպիսով, եթե մենք խնդիր դնենք՝ գտնել տվյալ պարագծի կորը, որը սահմանում է ամենամեծ տարածքը, ապա մենք խնդիր կունենանք տատանումների հաշվարկից, և ոչ թե այն հաշվարկից, որին դուք սովոր եք:

Այսպիսով, մենք ցանկանում ենք անցնել ինտեգրալը մարմնի անցած ճանապարհով: Եկեք դա անենք այսպես. Ամբողջ խնդիրն այն է, որ պատկերացնենք, որ կա ճշմարիտ ուղի, և որ ցանկացած այլ կոր, որը մենք գծում ենք, իրական ուղին չէ, այնպես որ, եթե հաշվարկենք դրա գործողությունը, կստանանք ավելի մեծ թիվ, քան մենք ստանում ենք համապատասխան գործողության համար: դեպի իրական ճանապարհ:

Այսպիսով, խնդիրն է գտնել ճշմարիտ ճանապարհը: Որտե՞ղ է այն ընկած: Ճանապարհներից մեկն, իհարկե, կլիներ հաշվել գործողությունները միլիոնավոր և միլիոնավոր ուղիների համար և հետո տեսնել, թե որ ճանապարհն ունի ամենափոքր գործողությունը: Սա այն ճանապարհն է, որում գործողությունը նվազագույն է և իրական կլինի:

Այս մեթոդը միանգամայն հնարավոր է։ Այնուամենայնիվ, դա կարելի է անել ավելի պարզ. Եթե ​​կա մի մեծություն, որն ունի նվազագույնը (սովորական ֆունկցիաներից, ասենք, ջերմաստիճանը), ապա նվազագույնի հատկություններից մեկն այն է, որ նրանից հեռավորության վրա հեռանալիս. առաջինփոքրության կարգով ֆունկցիան իր նվազագույն արժեքից շեղվում է միայն քանակով երկրորդպատվեր. Եվ կորի ցանկացած այլ վայրում փոքր հեռավորության վրա տեղաշարժը փոխում է ֆունկցիայի արժեքը նաև փոքրության առաջին կարգի արժեքով: Բայց նվազագույնը, կողմի աննշան շեղումները չեն հանգեցնում գործառույթի փոփոխության որպես առաջին մոտարկում:

Հենց այս հատկությունն է, որ մենք պատրաստվում ենք օգտագործել իրական ճանապարհը հաշվարկելու համար:

Եթե ​​ուղին ճիշտ է, ապա դրանից մի փոքր տարբերվող կորը, որպես առաջին մոտարկում, չի հանգեցնի գործողության մեծության փոփոխությանը: Բոլոր փոփոխությունները, եթե դա իսկապես նվազագույնն էր, կհայտնվեն միայն երկրորդ մոտարկումով:

Սա հեշտ է ապացուցել։ Եթե ​​կորից որոշակի շեղումներով փոփոխություններ են տեղի ունենում առաջին կարգով, ապա այդ փոփոխություններն ուժի մեջ են համամասնականշեղում. Նրանք, ամենայն հավանականությամբ, կբարձրացնեն ազդեցությունը. հակառակ դեպքում դա նվազագույն չէր լինի: Բայց մեկ անգամ փոփոխությունները համամասնականշեղումը, ապա շեղման նշանը փոխելը կնվազեցնի գործողությունը: Ստացվում է, որ երբ շեղվում ես մեկ ուղղությամբ, ազդեցությունը մեծանում է, իսկ երբ շեղվում ես հակառակ ուղղությամբ՝ նվազում։ Միակ հնարավորությունը, որ դա իսկապես նվազագույն լինի, այն է, որ, որպես առաջին մոտարկում, փոփոխություններ տեղի չեն ունենում, և փոփոխությունները համաչափ են իրական ուղուց շեղման քառակուսու հետ:

Այսպիսով, մենք կգնանք հետևյալ ճանապարհով՝ նշելով x(տ) (ներքևում տողով) ճշմարիտ ուղին այն է, որը մենք ուզում ենք գտնել: Եկեք փորձնական վազք կատարենք x(տ), ցանկալիից տարբերվելով փոքր քանակությամբ, որը մենք նշում ենք η (տ).

Գաղափարն այն է, որ եթե հաշվենք գործողությունը Ս ճանապարհին x(տ), ապա սրա միջև եղած տարբերությունը Ս և այն գործողությամբ, որը մենք հաշվարկել ենք ճանապարհի համար x(տ) (պարզության համար այն կնշանակվի Ս), կամ տարբերությունը Ս_ Եվ Ս, պետք է լինի առաջին մոտարկումը η զրո. Նրանք կարող են տարբերվել երկրորդ կարգով, բայց առաջինում տարբերությունը պետք է լինի զրո:

Եվ սա պետք է պահպանել բոլորի համար η . Այնուամենայնիվ, ոչ բոլորի համար: Մեթոդը պահանջում է հաշվի առնել միայն այն ուղիները, որոնք բոլորը սկսվում և ավարտվում են միևնույն զույգ կետերով, այսինքն՝ յուրաքանչյուր ճանապարհ պետք է սկսվի տվյալ պահին։ տ 1 և ավարտվի տվյալ պահին մեկ այլ կոնկրետ կետում տ 2 . Այս կետերն ու պահերը գրանցվում են: Այսպիսով, մեր ֆունկցիան դ) (շեղումը) պետք է զրո լինի երկու ծայրերում. η (տ 1 )= 0 Եվ η (t 2)=0. Այս պայմանով մեր մաթեմատիկական խնդիրը դառնում է ամբողջությամբ սահմանված։

Եթե ​​դուք չգիտեիք հաշվարկը, կարող եք նույն բանն անել՝ սովորական ֆունկցիայի նվազագույնը գտնելու համար զ(x). Կմտածե՞ք, թե ինչ կլիներ, եթե վերցնեիք զ(x) և ավելացնել Xփոքր գումար հ, և կպնդի, որ փոփոխությունը զ(x) առաջին կարգով հ պետք է լինի նվազագույնը զրոյի: Կարո՞ղ եք ինձ ստեղծել x+հ փոխարեն Xև կընդլայնի j(x+h) մինչև առաջին հզորությունը հ. . ., մի խոսքով, կկրկնի այն ամենը, ինչով մենք մտադիր ենք անել η .

Եթե ​​հիմա ուշադիր նայենք դրան, ապա կտեսնենք, որ այստեղ գրված առաջին երկու տերմինները համապատասխանում են այդ գործողությանը Ս, որը ես կգրեի փնտրվող ճշմարիտ ճանապարհի համար X.Ես ուզում եմ ձեր ուշադրությունը կենտրոնացնել փոփոխությունների վրա: Ս, այսինքն միջև տարբերության վրա Ս եւ այսպես Ս_, որը կհանգեցնի ճշմարիտ ճանապարհին: Այս տարբերությունը կգրենք այսպես bS և եկեք դա անվանենք տարբերակ Ս. Հրաժարվելով «երկրորդ և ավելի բարձր պատվերներից», մենք ստանում ենք σS

Այժմ առաջադրանքն այսպիսի տեսք ունի. Ահա իմ առջև ինչ-որ անբաժանելի է: Ես դեռ չգիտեմ, թե ինչպիսին է այն, բայց հաստատ գիտեմ, որ, ինչ η Ինչ էլ որ լինի, այս ինտեգրալը պետք է հավասար լինի զրոյի։ «Դե», կարող եք մտածել, «միակ ճանապարհը, որ դա տեղի ունենա, բազմապատկիչն է η հավասար էր զրոյի»։ Բայց ինչ վերաբերում է առաջին ժամկետին, որտեղ կա դ η / dt? Դուք ասում եք. «Եթե η վերածվում է ոչնչի, ապա դրա ածանցյալը նույնն է՝ ոչինչ. սա նշանակում է գործակիցը ժամը dv\/ dt պետք է նաև զրո լինի»։ Դե, դա ամբողջովին ճիշտ չէ: Սա լիովին ճիշտ չէ, քանի որ շեղումների միջև η և դրա ածանցյալը կապ կա. նրանք լիովին անկախ չեն, քանի որ η (տ) պետք է լինի զրո և t 1 և ժամը տ 2 .


Տատանումների հաշվարկի բոլոր խնդիրները լուծելիս միշտ օգտագործվում է նույն ընդհանուր սկզբունքը։ Դուք մի փոքր փոխում եք այն, ինչ ցանկանում եք փոխել (նման է այն, ինչ մենք արեցինք ավելացնելով η ), հայացք առաջին կարգի պայմաններին, ապադասավորեք ամեն ինչ այնպես, որ ստացեք ինտեգրալ հետևյալ ձևով՝ «հերթափոխ (η ), բազմապատկված է ստացվածով», բայց այնպես, որ այն չի պարունակում որևէ ածանցյալ η (ոչ դ η / dt). Բացարձակապես անհրաժեշտ է ամեն ինչ վերափոխել, որպեսզի «ինչ-որ բան» մնա՝ բազմապատկված η . Այժմ դուք կհասկանաք, թե ինչու է դա այդքան կարևոր: (Կան բանաձևեր, որոնք ձեզ կասեն, թե ինչպես որոշ դեպքերում կարող եք դա անել առանց որևէ հաշվարկի, բայց դրանք այնքան էլ ընդհանուր չեն, որ արժե անգիր անել. լավագույնն է հաշվարկներն անել այնպես, ինչպես մենք ենք անում):

Ինչպես կարող եմ վերանորոգել առնանդամը դ η / dt, այնպես, որ հայտնվի η ? Ես կարող եմ դրան հասնել՝ մաս առ մաս ինտեգրվելով: Ստացվում է, որ տատանումների հաշվարկում ամբողջ հնարքը տատանումները նկարագրելն է Ս և այնուհետև ինտեգրվել ըստ մասերի, որպեսզի ածանցյալները η անհետացել է. Բոլոր խնդիրներում, որոնցում հայտնվում են ածանցյալներ, կատարվում է նույն հնարքը։

Հիշեք մասերի ինտեգրման ընդհանուր սկզբունքը: Եթե ​​ունեք կամայական f ֆունկցիա՝ բազմապատկած դ η / dt և ինտեգրված տ, ապա գրում ես ածանցյալը η /տ

Ինտեգրման սահմանները պետք է փոխարինվեն առաջին տերմինով t 1 Եվ տ 2 . Այնուհետև ինտեգրալի տակ ես կստանամ տերմինը ինտեգրումից ըստ մասերի և վերջին տերմինը, որը մնում է անփոփոխ փոխակերպման ընթացքում:
Եվ հիմա տեղի է ունենում այն, ինչ միշտ տեղի է ունենում՝ անհետանում է ինտեգրված մասը։ (Իսկ եթե չվերանա, ապա սկզբունքը պետք է վերաձեւակերպել՝ ավելացնելով նման անհետացում ապահովող պայմաններ։) Մենք արդեն ասել ենք, որ. η ճանապարհի ծայրերում պետք է հավասար լինի զրոյի: Ի վերջո, ո՞րն է մեր սկզբունքը։ Փաստն այն է, որ գործողությունը նվազագույն է, պայմանով, որ բազմազան կորը սկսվի և ավարտվի ընտրված կետերում: Դա նշանակում է որ η (t 1)=0 և η (t 2)=0. Հետևաբար, ինտեգրված տերմինը զրո է: Մնացած անդամներին հավաքում ենք ու գրում

Վարիացիա Ս այժմ ստացել է այն ձևը, որը մենք ուզում էինք տալ. ինչ-որ բան փակագծերում է (նշենք Ֆ), և այս ամենը բազմապատկվում է η (տ) և ինտեգրված է տ տ նախքան տ 2 .
Պարզվեց, որ որոշ արտահայտության ինտեգրալը բազմապատկվում է η (տ), միշտ հավասար է զրոյի.

Ինչ-որ գործառույթ կա՞ տ; Ես այն բազմապատկում եմ η (տ) և ինտեգրել այն սկզբից մինչև վերջ: Եվ ինչ էլ որ լինի η, Ես ստանում եմ զրո: Սա նշանակում է, որ ֆունկցիան Ֆ(տ) հավասար է զրոյի: Ընդհանուր առմամբ, սա ակնհայտ է, բայց ամեն դեպքում ես ձեզ ցույց կտամ դա ապացուցելու մեկ ճանապարհ:

Թող որպես η (տ) Ես կընտրեմ մի բան, որը հավասար է զրոյի ամենուր, բոլորի համար տ, բացառությամբ մեկ նախապես ընտրված արժեքի տ. Այն մնում է զրո, մինչև ես այնտեղ հասնեմ տ, սՀետո մի պահ ցատկում է ու անմիջապես հետ է ընկնում։ Եթե ​​վերցնենք այս մ) ինտեգրալը բազմապատկած ինչ-որ ֆունկցիայով Ֆ, միակ վայրը, որտեղ դուք կստանաք ոչ զրոյական բան, այն է, որտեղ η (տ) վեր թռավ; և դուք կստանաք արժեքը Ֆ այս պահին ինտեգրալի վրա ցատկի վրայով: Ինտեգրալն ինքնին ցատկի վրայով հավասար չէ զրոյի, այլ բազմապատկելուց հետո Ֆ այն պետք է զրո տա: Սա նշանակում է, որ ֆունկցիան այն վայրում, որտեղ ցատկ է եղել, պետք է զրո լինի։ Բայց ցատկը կարող էր լինել ամենուր. Նշանակում է, Ֆ ամենուր պետք է զրո լինի:

Մենք տեսնում ենք, որ եթե մեր ինտեգրալը հավասար է զրոյի որևէ մեկի համար η , ապա գործակիցը ժամը η պետք է գնա զրոյի: Գործողությունների ինտեգրալը հասնում է նվազագույնի ճանապարհին, որը կբավարարի այսպիսի բարդ դիֆերենցիալ հավասարումը.

Դա իրականում այնքան էլ բարդ չէ. դու նախկինում հանդիպել ես նրան: Դա պարզապես F=ma է: Առաջին տերմինը զանգվածային անգամ արագացումն է. երկրորդը պոտենցիալ էներգիայի ածանցյալն է, այսինքն՝ ուժը:

Այսպիսով, մենք ցույց տվեցինք (գոնե պահպանողական համակարգի համար), որ նվազագույն գործողության սկզբունքը հանգեցնում է ճիշտ պատասխանի. նա նշում է, որ ուղին, որն ունի նվազագույն գործողություն, այն ուղին է, որը բավարարում է Նյուտոնի օրենքը:

Եվս մեկ դիտողություն է պետք անել. Ես սա չեմ ապացուցել նվազագույնը.Գուցե սա առավելագույնն է։ Փաստորեն, սա պարտադիր չէ, որ նվազագույնը լինի: Այստեղ ամեն ինչ նույնն է, ինչ «ամենակարճ ժամանակի սկզբունքով», որը մենք քննարկել ենք օպտիկա ուսումնասիրելիս։ Այնտեղ էլ նախ խոսեցինք «ամենակարճ» ժամանակի մասին։ Սակայն պարզվեց, որ կան իրավիճակներ, որոնցում այս ժամանակը պարտադիր չէ, որ «ամենակարճը» լինի։ Հիմնական սկզբունքն այն է, որ ցանկացած առաջին կարգի շեղումներօպտիկական ճանապարհից փոփոխություններըժամանակի ընթացքում հավասար կլիներ զրոյի; Այստեղ նույն պատմությունն է. «Նվազագույն» ասելով մենք իրականում նկատի ունենք, որ քանակի փոփոխության փոքրության առաջին կարգը Սերբ ուղուց շեղումները պետք է հավասար լինեն զրոյի: Եվ սա պարտադիր չէ, որ «նվազագույնը» լինի։

Հիմա ուզում եմ անցնել որոշ ընդհանրացումների։ Նախ, այս ամբողջ պատմությունը կարելի էր անել եռաչափ: Պարզի փոխարեն XԵս այդ ժամանակ կունենայի x, yԵվ զորպես գործառույթներ տ,և գործողությունը ավելի բարդ տեսք կունենա: 3D-ով շարժվելիս դուք պետք է օգտագործեք լիարժեք կինետիկ էներգիա). (t/2),բազմապատկված է ընդհանուր արագության քառակուսու վրա: Այլ կերպ ասած

Բացի այդ, պոտենցիալ էներգիան այժմ ֆունկցիա է x, yԵվ զ.Ի՞նչ կարող եք ասել ճանապարհի մասին: Ճանապարհը տարածության որոշակի ընդհանուր կոր է. նկարելն այնքան էլ հեշտ չէ, բայց գաղափարը մնում է նույնը։ Բա η? Դե, η-ն ունի նաև երեք բաղադրիչ. Ճանապարհը կարող է տեղաշարժվել և՛ x, և՛ in y,և ըստ z,կամ բոլոր երեք ուղղություններով միաժամանակ։ Այսպիսով η այժմ վեկտոր: Սա որևէ լուրջ բարդություն չի ստեղծում։ Միայն տատանումները պետք է հավասար լինեն զրոյի առաջին կարգըապա հաշվարկը կարող է իրականացվել հաջորդաբար երեք հերթափոխով: Նախ կարող եք շարժվել ցմիայն ուղղությամբ Xև ասեք, որ գործակիցը պետք է գնա զրոյի: Դուք ստանում եք մեկ հավասարում. Հետո մենք կտեղափոխվենք ցուղղությամբ ժամըև մենք ստանում ենք երկրորդը: Այնուհետև շարժվեք ուղղությամբ զև մենք ստանում ենք երրորդը: Դուք կարող եք ամեն ինչ անել, եթե ցանկանում եք, այլ հերթականությամբ: Ինչ էլ որ լինի, առաջանում է հավասարումների եռյակ։ Բայց Նյուտոնի օրենքը նաև երեք հավասարումներ է երեք հարթություններում, յուրաքանչյուր բաղադրիչի համար մեկը: Մնում է ինքներդ համոզվեք, որ այս ամենը գործում է եռաչափ (այստեղ շատ աշխատանք չկա): Ի դեպ, դուք կարող եք վերցնել ցանկացած կոորդինատային համակարգ, որը ցանկանում եք, բևեռային, ցանկացած, և անմիջապես ստանալ Նյուտոնի օրենքները այս համակարգի հետ կապված՝ հաշվի առնելով, թե ինչ է տեղի ունենում, երբ տեղի է ունենում տեղաշարժ: η շառավղով կամ անկյան երկայնքով և այլն:

Մեթոդը կարող է ընդհանրացվել կամայական թվով մասնիկների։ Եթե, ասենք, դուք ունեք երկու մասնիկ, և դրանց միջև կան որոշ ուժեր, և կա փոխադարձ պոտենցիալ էներգիա, ապա դուք պարզապես ավելացնում եք նրանց կինետիկ էներգիաները և գումարից հանում փոխազդեցության պոտենցիալ էներգիան: Ինչո՞վ եք տարբերվում: Ճանապարհներ երկուսն էլմասնիկներ. Այնուհետև երեք չափերով շարժվող երկու մասնիկների համար առաջանում են վեց հավասարումներ։ Դուք կարող եք փոխել 1-ին մասնիկի դիրքը ուղղությամբ X,ուղղությամբ ժամըև դեպի z,և նույնը արեք 2-րդ մասնիկի հետ, հետևաբար կան վեց հավասարումներ: Եվ այդպես էլ պետք է լինի։ Երեք հավասարումներ որոշում են մասնիկի 1-ի արագացումը նրա վրա ազդող ուժի շնորհիվ, իսկ մյուս երեքը որոշում են մասնիկի 2-ի արագացումը նրա վրա ազդող ուժի շնորհիվ: Միշտ հետևեք խաղի նույն կանոններին, և դուք կստանաք Նյուտոնի օրենքը կամայական թվով մասնիկների համար:

Ես ասացի, որ մենք կստանանք Նյուտոնի օրենքը: Սա լիովին ճիշտ չէ, քանի որ Նյուտոնի օրենքը ներառում է նաև ոչ պահպանողական ուժեր, ինչպիսիք են շփումը: Նյուտոնը պնդում էր, որ որհավասար է ցանկացած F: Նվազագույն գործողության սկզբունքը գործում է միայն պահպանողականհամակարգեր, որտեղ բոլոր ուժերը կարելի է ձեռք բերել պոտենցիալ ֆունկցիայից: Բայց դուք գիտեք, որ մանրադիտակային մակարդակում, այսինքն՝ ամենախոր ֆիզիկական մակարդակում, ոչ պահպանողական ուժեր գոյություն չունեն։ Ոչ պահպանողական ուժերը (օրինակ՝ շփումը) առաջանում են միայն այն պատճառով, որ մենք անտեսում ենք մանրադիտակային բարդ ազդեցությունները. պարզապես չափից շատ մասնիկներ կան վերլուծելու համար: Հիմնարարնույն օրենքները կարող էարտահայտվել որպես նվազագույն գործողության սկզբունք:

Անցնեմ հետագա ընդհանրացումների։ Ենթադրենք, մեզ հետաքրքրում է, թե ինչ կլինի, երբ մասնիկը հարաբերականորեն շարժվի։ Մինչ այժմ մենք չենք ստացել շարժման ճիշտ հարաբերական հավասարումը. F=ma ճշմարիտ է միայն ոչ հարաբերական շարժումների դեպքում: Հարց է առաջանում՝ կա՞ արդյոք հարաբերականության դեպքում նվազագույն գործողության համապատասխան սկզբունք։ Այո, այն գոյություն ունի։ Հարաբերականության դեպքում բանաձևը հետևյալն է.

Գործողությունների ինտեգրալի առաջին մասը մնացած զանգվածի արտադրյալն է t 0վրա 2-իցև արագության ֆունկցիայի ինտեգրալին √ (1- v 2 / գ 2 ). Այնուհետև, պոտենցիալ էներգիան հանելու փոխարեն, մենք ունենք սկալյար պոտենցիալի φ և վեկտորային ներուժի ինտեգրալներ A անգամ v. Իհարկե, այստեղ հաշվի են առնվում միայն էլեկտրամագնիսական ուժերը։ Բոլոր էլեկտրական և մագնիսական դաշտերը արտահայտված են φ և A-ներով: Այս գործողության ֆունկցիան տալիս է էլեկտրամագնիսական դաշտում առանձին մասնիկի հարաբերական շարժման ամբողջական տեսություն:

Իհարկե, պետք է հասկանալ, որ որտեղ ես գրել եմ v, նախքան հաշվարկներ անելը, պետք է փոխարինել dx/ dt փոխարեն v x և այլն: Ավելին, որտեղ ես պարզապես գրել եմ x, y, z,պետք է տվյալ պահին պատկերացնել կետերը տ: x(տ), y(տ), զ(տ). Իրականում միայն v-ի նման փոխարինումներից և փոխարինումներից հետո դուք կստանաք հարաբերական մասնիկի գործողության բանաձև։ Թող ձեզանից ամենահմուտը փորձի ապացուցել, որ գործողության այս բանաձեւն իրականում տալիս է հարաբերականության տեսության շարժման ճիշտ հավասարումները: Ուղղակի խորհուրդ կտամ սկսել Ա-ից հրաժարվելով, այսինքն՝ առայժմ անել առանց մագնիսական դաշտերի։ Այնուհետև դուք պետք է ստանաք շարժման հավասարման բաղադրիչները dp/dt=—qVφ,որտեղ, ինչպես հավանաբար հիշում եք, p=mv√(1-v 2 /c 2):

Շատ ավելի դժվար է հաշվի առնել վեկտորային պոտենցիալ Ա-ն: Հետո տատանումները դառնում են անհամեմատ ավելի բարդ։ Բայց վերջում ստացվում է, որ ուժը հավասար է նրան, ինչ պետք է լինի՝ g(E+v × B): Բայց ինքներդ ձեզ հետ զվարճացեք:

Ուզում եմ շեշտել, որ ընդհանուր դեպքում (օրինակ՝ հարաբերական բանաձևում) գործողության մեջ գտնվող ինտեգրալն այլևս չի ներառում կինետիկ և պոտենցիալ էներգիաների տարբերությունը։ Սա հարմար էր միայն ոչ հարաբերական մոտավորության դեպքում: Օրինակ՝ անդամ m o c 2√(1-v 2 /c 2)-Սա այն չէ, ինչ կոչվում է կինետիկ էներգիա: Հարցը, թե ինչ գործողություն պետք է լինի որևէ կոնկրետ դեպքի համար, կարող է որոշվել փորձարկումից և սխալից հետո: Սա նույն տեսակի խնդիր է, ինչ շարժման հավասարումները որոշելը: Պարզապես պետք է խաղալ ձեր իմացած հավասարումների հետ և տեսնել, թե արդյոք դրանք կարող են գրվել որպես նվազագույն գործողության սկզբունք:

Եվս մեկ նշում տերմինաբանության մասին. Այդ ֆունկցիան, որը ժամանակի ընթացքում ինտեգրվում է գործողություն ստանալու համար Ս,կանչեց ԼագրանժյանԼ. Սա ֆունկցիա է, որը կախված է միայն մասնիկների արագություններից և դիրքերից։ Այսպիսով, նվազագույն գործողության սկզբունքը նույնպես գրված է ձևի մեջ

որտեղ տակ X եսԵվ v i ենթադրվում են կոորդինատների և արագությունների բոլոր բաղադրիչները: Եթե ​​երբևէ լսում եք, որ ինչ-որ մեկը խոսում է «Լագրանժի» մասին, նրանք խոսում են այն գործառույթի մասին, որն օգտագործվում է ձեռք բերելու համար Ս. Էլեկտրամագնիսական դաշտում հարաբերական շարժման համար

Բացի այդ, նշեմ, որ ամենաբծախնդիր ու մանկամիտ մարդիկ չեն զանգում Սգործողություն. Այն կոչվում է «Հեմիլթոնի առաջին հիմնական գործառույթը»։ Բայց «Հեմիլթոնի ամենանվազագույն հիմնական գործառույթի սկզբունքը» թեմայով դասախոսություն կարդալն իմ ուժերից վեր էր: Ես դա անվանեցի «գործողություն»: Եվ բացի այդ, ավելի ու ավելի շատ մարդիկ դա անվանում են «գործողություն»: Տեսեք, պատմականորեն գործողությունը կոչվում է այլ բան, որն այնքան էլ օգտակար չէ գիտությանը, բայց ես կարծում եմ, որ ավելի իմաստալից է փոխել սահմանումը: Այժմ դուք նույնպես կսկսեք նոր գործառույթն անվանել գործողություն, և շուտով բոլորը կսկսեն այն անվանել այս պարզ անունով:

Հիմա ես ուզում եմ ձեզ մի բան պատմել մեր թեմայի մասին, որը նման է այն պատճառաբանությանը, որը ես ունեի ամենակարճ ժամանակի սկզբունքի մասին։ Օրենքի բուն էության մեջ կա տարբերություն, որն ասում է, որ մի կետից մյուսը վերցված ինչ-որ ինտեգրալ ունի նվազագույնը. օրենքը, որը մեզ ինչ-որ բան է ասում միանգամից ամբողջ ճանապարհի մասին, և այն օրենքը, որն ասում է, որ երբ շարժվում ես, ապա Սա նշանակում է, որ կա ուժ, որը տանում է դեպի արագացում: Երկրորդ մոտեցումը ձեզ զեկուցում է ձեր յուրաքանչյուր քայլի մասին, այն հետևում է ձեր ճանապարհը դյույմ առ դյույմ, և առաջինը անմիջապես տալիս է որոշակի ընդհանուր հայտարարություն ամբողջ անցած ճանապարհի մասին: Լույսի մասին խոսելիս խոսեցինք այս երկու մոտեցումների կապի մասին։ Հիմա ես ուզում եմ ձեզ բացատրել, թե ինչու պետք է գոյություն ունենան դիֆերենցիալ օրենքներ, եթե կա այդպիսի սկզբունք՝ նվազագույն գործողության սկզբունքը: Պատճառը սա է. եկեք դիտարկենք իրականում անցած ճանապարհը տարածության և ժամանակի մեջ: Ինչպես նախկինում, մենք կբավարարվենք մեկ չափումով, որպեսզի կարողանանք գծել կախվածության գրաֆիկը X-ից տ. Ճշմարիտ ճանապարհով Ս հասնում է նվազագույնի. Ենթադրենք, որ մենք ունենք այս ճանապարհը և այն անցնում է ինչ-որ կետով Ատարածության և ժամանակի և մեկ այլ հարևան կետի միջոցով բ.

Այժմ, եթե ամբողջ ինտեգրալը t 1 նախքան տ 2 հասել է նվազագույնի, անհրաժեշտ է, որ ինտեգրալը փոքր հատվածի երկայնքով a-ից մինչև բ նույնպես նվազագույն էր: Դա չի կարող լինել այդ մասը Անախքան բնվազագույնից մի փոքր ավելին: Հակառակ դեպքում, դուք կարող եք այս հատվածում ետ ու առաջ շարժել կորը և մի փոքր նվազեցնել ամբողջ ինտեգրալի արժեքը:

Սա նշանակում է, որ ուղու ցանկացած հատված նույնպես պետք է նվազագույնը ապահովի: Եվ սա ճիշտ է ճանապարհի ցանկացած փոքր հատվածի համար: Հետևաբար, սկզբունքը, որ ամբողջ ճանապարհը պետք է տա ​​նվազագույնը, կարելի է ձևակերպել՝ ասելով, որ ուղու անվերջ փոքր հատվածը նույնպես կոր է, որի վրա գործողությունը նվազագույն է։ Եվ եթե վերցնենք ուղու բավական կարճ հատվածը` միմյանց շատ մոտ կետերի միջև ԱԵվ բ,- ապա կարևոր չէ, թե ինչպես է ներուժը փոխվում կետից կետ այս վայրից հեռու, քանի որ, անցնելով ձեր ամբողջ կարճ հատվածը, դուք գրեթե երբեք չեք շարժվում այդ վայրից: Միակ բանը, որ դուք պետք է հաշվի առնեք, ներուժի փոքրության առաջին կարգի փոփոխությունն է: Պատասխանը կարող է կախված լինել միայն ներուժի ածանցյալից, այլ ոչ թե այլ տեղ պոտենցիալից: Այսպիսով, ամբողջ ուղու հատկության մասին հայտարարությունը որպես ամբողջություն դառնում է հայտարարություն այն մասին, թե ինչ է տեղի ունենում ճանապարհի կարճ հատվածում, այսինքն՝ դիֆերենցիալ հայտարարություն: Եվ այս դիֆերենցիալ ձևակերպումը ներառում է ներուժի ածանցյալներ, այսինքն՝ ուժը տվյալ կետում։ Սա ընդհանուր օրենքի և դիֆերենցիալ օրենքի կապի որակական բացատրությունն է։

Երբ խոսում էինք լույսի մասին, քննարկում էինք նաև այն հարցը՝ ինչպե՞ս է մասնիկը գտնում ճիշտ ուղին: Դիֆերենցիալ տեսանկյունից դա հեշտ է հասկանալ: Ամեն պահի մասնիկը զգում է արագացում և գիտի միայն այն, ինչ պետք է անի այդ պահին: Բայց պատճառի և հետևանքի ձեր բոլոր բնազդները արթնանում են, երբ լսում եք, որ մասնիկը «որոշում է», թե որ ճանապարհն է գնալու՝ ձգտելով նվազագույն գործողության: Արդյո՞ք նա «շնչում է» հարևան ճանապարհները՝ պարզելով, թե ինչի կհանգեցնեն դրանք՝ քիչ թե շատ գործողության: Երբ լույսի ուղու վրա էկրան դրեցինք, որպեսզի ֆոտոնները չկարողանան փորձել բոլոր ուղիները, պարզեցինք, որ նրանք չեն կարող որոշել, թե որ ճանապարհն են անցնելու, և ստացանք դիֆրակցիայի ֆենոմենը։

Բայց արդյո՞ք դա ճիշտ է նաև մեխանիկայի համար: Ճի՞շտ է, որ մասնիկը ոչ միայն «գնում է ճիշտ ճանապարհով», այլ վերանայում է մնացած բոլոր հնարավոր հետագծերը: Իսկ եթե, խոչընդոտներ դնելով նրա ճանապարհին, թույլ չտանք նայել առաջ, ապա կստանանք դիֆրակցիայի երեւույթի ինչ-որ անալոգը։ Այս ամենի մեջ ամենահիասքանչն այն է, որ ամեն ինչ իսկապես այսպիսին է. Սա հենց այն է, ինչ ասում են քվանտային մեխանիկայի օրենքները։ Այսպիսով, մեր նվազագույն գործողությունների սկզբունքը լիովին ձևակերպված չէ: Այն բաղկացած է ոչ թե նրանից, որ մասնիկը ընտրում է նվազագույն գործողության ուղին, այլ այն, որ նա «զգում է» բոլոր հարևան ուղիները և ընտրում է այն մեկը, որի երկայնքով գործողությունը նվազագույն է, և այս ընտրության մեթոդը նման է. եղանակը, որով լույսն ընտրում է ամենակարճ ժամանակը: Դուք հիշում եք, որ լույսը ընտրում է ամենակարճ ժամանակը հետևյալն է. Իսկ ընդհանուր ամպլիտուդը ինչ-որ կետում ամպլիտուդային ներդրումների գումարն է բոլոր այն ուղիների համար, որոնցով լույսը կարող է հասնել դրան: Բոլոր այն ուղիները, որոնց փուլերը կտրուկ տարբերվում են, ավելացումից հետո ոչինչ չեն տալիս։ Բայց եթե ձեզ հաջողվի գտնել ուղիների ամբողջ հաջորդականությունը, որոնց փուլերը գրեթե նույնն են, ապա փոքր ներդրումները կավելանան, և ժամանման կետում ընդհանուր ամպլիտուդը նկատելի արժեք կստանա: Ամենակարևոր ճանապարհը այն ճանապարհն է, որի մոտ կան շատ մոտ ճանապարհներ, որոնք տալիս են նույն փուլը:

Ճիշտ նույն բանը տեղի է ունենում քվանտային մեխանիկայում։ Ամբողջական քվանտային մեխանիկա (ոչ հարաբերական և անտեսող էլեկտրոնի սպին) աշխատում է այսպես. հավանականություն, որ մասնիկը հեռանում է կետից. 1 այդ պահին t 1, կհասնի կետին 2 այդ պահին տ 2 , հավասար է հավանականության ամպլիտուդի քառակուսին: Ընդհանուր ամպլիտուդը կարող է գրվել որպես բոլոր հնարավոր ուղիների ամպլիտուդների գումար՝ ցանկացած ժամանման ճանապարհի համար: Որևէ մեկի համար x(տ), որը կարող է առաջանալ ցանկացած երևակայական հետագծի համար, պետք է հաշվարկել ամպլիտուդը: Այնուհետեւ նրանք բոլորը պետք է ծալվեն: Ի՞նչ ենք մենք ընդունում որպես որոշակի ճանապարհի հավանականության ամպլիտուդ: Մեր գործողությունների ինտեգրալը մեզ հուշում է, թե ինչ պետք է լինի անհատական ​​ուղու լայնությունը: Լայնությունը համաչափ է e tS/h, Որտեղ Ս - գործողություն այս ճանապարհով: Սա նշանակում է, որ եթե ամպլիտուդի փուլը ներկայացնենք կոմպլեքս թվով, ապա ֆազային անկյունը հավասար կլինի Ս/ հ. Գործողություն Ս ժամանակի ընթացքում ունի էներգիայի չափ, իսկ Պլանկի հաստատունը նույն չափումն ունի։ Սա այն հաստատունն է, որը որոշում է, թե երբ է անհրաժեշտ քվանտային մեխանիկա:

Եվ ամեն ինչ այդպես է աշխատում: Թող գործողություններ կատարվեն բոլոր ուղիների համար Ս թվի համեմատ շատ մեծ կլինի հ. Թող ինչ-որ ճանապարհ տանի դեպի որոշակի ամպլիտուդի արժեք: Հարակից ճանապարհի փուլը բոլորովին այլ կլինի, քանի որ հսկայական Ս նույնիսկ աննշան փոփոխություններ Ս կտրուկ փոխել փուլը (ի վերջո հչափազանց քիչ): Սա նշանակում է, որ հարակից ուղիները սովորաբար մարում են իրենց ներդրումը, երբ ավելացվում են: Եվ միայն մի ոլորտում է դա ճիշտ չէ, այն դեպքում, որտեղ և՛ ուղին, և՛ նրա հարևանը, երկուսն էլ, առաջին մոտավորությամբ, ունեն նույն փուլը (կամ, ավելի ճիշտ, գրեթե նույն գործողությունը, որը տարբերվում է ներսում: ը):Հաշվի են առնվում միայն այդպիսի ուղիները։ Իսկ սահմանափակող դեպքում, երբ Պլանկի հաստատունը հհակված է զրոյի, ճիշտ քվանտային մեխանիկական օրենքները կարելի է ամփոփել այսպես. «Մոռացեք բոլոր հավանականության ամպլիտուդների մասին: Մասնիկը իրականում շարժվում է հատուկ ճանապարհով, հենց այն ճանապարհով, որի երկայնքով Ս առաջին մոտավորությունը չի փոխվում»: Սա նվազագույն գործողության սկզբունքի և քվանտային մեխանիկայի միջև կապն է: Այն, որ քվանտային մեխանիկա կարելի է այսպես ձևակերպել, 1942 թվականին հայտնաբերել է նույն ուսուցչի՝ պարոն Բադերի աշակերտը, որի մասին ես պատմեցի։ [Քվանտային մեխանիկա ի սկզբանե ձևակերպվել է ամպլիտուդի դիֆերենցիալ հավասարման միջոցով (Շրյոդինգեր), ինչպես նաև որոշ մատրիցային մաթեմատիկա (Հայզենբերգ):

Հիմա ես ուզում եմ խոսել ֆիզիկայում նվազագույնի այլ սկզբունքների մասին։ Այս տեսակի շատ հետաքրքիր սկզբունքներ կան: Չթվարկեմ բոլորը, բայց նշեմ ևս մեկը։ Ավելի ուշ, երբ հասնենք մեկ ֆիզիկական երևույթի, որի համար կա գերազանց նվազագույն սկզբունք, ես ձեզ կասեմ դրա մասին։ Այժմ ես ուզում եմ ցույց տալ, որ անհրաժեշտ չէ նկարագրել էլեկտրաստատիկան՝ օգտագործելով դաշտի դիֆերենցիալ հավասարումը. Փոխարենը կարելի է պահանջել, որ որոշ ինտեգրալներ ունենան առավելագույն կամ նվազագույն: Սկսենք, եկեք վերցնենք այն դեպքը, երբ լիցքի խտությունը հայտնի է ամենուր, բայց մենք պետք է գտնենք φ պոտենցիալը տարածության ցանկացած կետում։ Դուք արդեն գիտեք, որ պատասխանը պետք է լինի.

Նույն բանն ասելու մեկ այլ տարբերակ ինտեգրալը գնահատելն է U*

սա ծավալային ինտեգրալ է: Այն վերցված է ողջ տարածության վրա: Պոտենցիալ ճիշտ բաշխմամբ φ (x, y,զ) այս արտահայտությունը հասնում է իր նվազագույնի:

Մենք կարող ենք ցույց տալ, որ այս երկու պնդումներն էլ էլեկտրաստատիկության վերաբերյալ համարժեք են: Ենթադրենք, որ մենք ընտրել ենք կամայական φ ֆունկցիա։ Մենք ուզում ենք ցույց տալ, որ երբ որպես φ վերցնում ենք _φ պոտենցիալի ճիշտ արժեքը գումարած մի փոքր շեղում f, ապա փոքրության առաջին կարգի փոփոխությունը U* հավասար կլինի զրոյի։ Այսպիսով, մենք գրում ենք

այստեղ φ-ն այն է, ինչ մենք փնտրում ենք. բայց մենք կփոփոխենք φ՝ տեսնելու համար, թե ինչ պետք է լինի այն տատանումների համար U* պարզվեց, որ փոքրության առաջին կարգի է: Առաջին կիսամյակում U* մենք պետք է գրենք

Սա պետք է ինտեգրվի x, yև ըստ զ. Եվ այստեղ նույն հնարքն ինքնին հուշում է՝ ազատվելու համար Դ Ֆ/ dx, մենք ինտեգրվելու ենք Xմասերով. Սա կհանգեցնի լրացուցիչ տարբերակմանφ նկատմամբ X.Սա նույն հիմնական գաղափարն է, որով մենք ազատվեցինք ածանցյալներից տ. Մենք օգտագործում ենք հավասարությունը

Ինտեգրված տերմինը զրոյական է, քանի որ f-ն անվերջության դեպքում զրո է: (Սա համապատասխանում է η անհետացողին որպես տ 1 Եվ տ 2 . Այսպիսով, մեր սկզբունքը ավելի ճշգրիտ ձևակերպված է հետևյալ կերպ. U* իրավունքի համար φ ավելի քիչ, քան մյուսների համար φ(x, y,զ), ունենալով նույն արժեքները անսահմանության ժամանակ:) Այնուհետև մենք նույնը կանենք ժամըև զ. Մեր ինտեգրալ ΔU* կվերածվի

Որպեսզի այս փոփոխությունը հավասար լինի զրոյի ցանկացած կամայական f-ի համար, f-ի գործակիցը պետք է հավասար լինի զրոյի։ Նշանակում է,

Մենք վերադառնում ենք մեր հին հավասարմանը: Սա նշանակում է, որ մեր «նվազագույն» առաջարկը ճիշտ է։ Այն կարող է ընդհանրացվել, եթե հաշվարկները մի փոքր փոփոխվեն: Եկեք հետ գնանք և մաս առ մաս ինտեգրենք՝ առանց ամեն ինչ բաղադրիչ առ բաղադրիչ նկարագրելու։ Սկսենք գրելով հետևյալ հավասարությունը.

Ձախ կողմը տարբերակելով՝ կարող եմ ցույց տալ, որ այն ճիշտ հավասար է աջին։ Այս հավասարումը հարմար է մասերով ինտեգրում կատարելու համար: Մեր ինտեգրալում ΔU* փոխարինում ենք Vφ*Vf nև fV 2 φ+V*(fVφ) և այնուհետև ինտեգրեք սա ծավալի վրա: Ծավալի վրա ինտեգրվելուց հետո տարաձայնության տերմինը փոխարինվում է մակերեսի վրա ինտեգրալով.

Եվ քանի որ մենք ինտեգրվում ենք ամբողջ տարածության վրա, այս ինտեգրալի մակերեսը գտնվում է անսահմանության մեջ: Սա նշանակում է f=0, և մենք ստանում ենք նույն արդյունքը:

Միայն հիմա ենք մենք սկսում հասկանալ, թե ինչպես լուծել խնդիրները, որոնցում մենք մենք չգիտենքորտեղ գտնվում են բոլոր մեղադրանքները: Եկեք ունենանք հաղորդիչներ, որոնց վրա ինչ-որ կերպ բաշխվում են լիցքերը։ Եթե ​​բոլոր հաղորդիչների պոտենցիալները ամրագրված են, ապա մեր նվազագույն սկզբունքը դեռ թույլատրվում է կիրառել: Ինտեգրում U* մենք գծելու ենք միայն բոլոր դիրիժորներից դուրս ընկած տարածքի երկայնքով: Բայց քանի որ մենք չենք կարող փոխել (φ) դիրիժորների վրա, ապա դրանց մակերևույթի վրա f = 0, իսկ մակերեսի ինտեգրալը

անհրաժեշտ է անել միայն հաղորդիչների միջև ընկած տարածություններում: Եվ մենք, իհարկե, նորից ստանում ենք Պուասոնի հավասարումը

Ուստի մենք ցույց տվեցինք, որ մեր սկզբնական ինտեգրալը U* հասնում է նվազագույնի նույնիսկ այն դեպքում, երբ այն հաշվարկվում է հաղորդիչների միջև տարածության մեջ, որոնցից յուրաքանչյուրը գտնվում է ֆիքսված պոտենցիալում [սա նշանակում է, որ յուրաքանչյուր փորձնական ֆունկցիա φ(g, y,զ) պետք է հավասար լինի նշված հաղորդիչի ներուժին, երբ (x, y,զ) - դիրիժորի մակերեսի կետերը]: Հետաքրքիր առանձնահատուկ դեպք կա, երբ լիցքերը տեղադրված են միայն հաղորդիչների վրա։ Հետո

և մեր նվազագույն սկզբունքը մեզ ասում է, որ այն դեպքում, երբ յուրաքանչյուր դիրիժոր ունի իր նախապես որոշված ​​պոտենցիալը, նրանց միջև եղած տարածությունների պոտենցիալները ճշգրտվում են այնպես, որ ինտեգրալը U* ստացվում է հնարավորինս փոքր: Ինչպիսի՞ ինտեգրալ է սա: Vφ տերմինը էլեկտրական դաշտն է։ Սա նշանակում է, որ ինտեգրալը էլեկտրաստատիկ էներգիա է։ Ճիշտ դաշտը միակն է, որը, որպես պոտենցիալ գրադիենտ ստացված բոլոր դաշտերից, ունի ամենացածր ընդհանուր էներգիան:

Ես կցանկանայի օգտագործել այս արդյունքը որոշակի խնդիր լուծելու համար և ցույց տալ ձեզ, որ այս ամենն իրական գործնական նշանակություն ունի: Ենթադրենք, ես վերցրեցի երկու հաղորդիչ գլանաձեւ կոնդենսատորի տեսքով:

Ներքին հաղորդիչը ունի պոտենցիալ, որը հավասար է, ասենք. Վ, իսկ արտաքինի համար՝ զրո։ Թող ներքին հաղորդիչի շառավիղը հավասար լինի Ա,և արտաքին - բ.Այժմ կարելի է ենթադրել, որ պոտենցիալների բաշխվածությունը նրանց միջև է ցանկացած.Բայց եթե վերցնենք ճիշտφ-ի արժեքը և հաշվարկել
(ε 0 /2) ∫ (Vφ) 2 դՎապա համակարգի էներգիան պետք է լինի 1/2CV 2:

Այսպիսով, օգտագործելով մեր սկզբունքը, կարող եք հաշվարկել հզորությունը ՀԵՏ.Եթե ​​վերցնենք պոտենցիալների սխալ բաշխում և փորձենք գնահատել կոնդենսատորի հզորությունը՝ օգտագործելով այս մեթոդը, մենք կհասնենք չափազանց մեծ հզորության արժեքի ֆիքսվածի համար։ Վ. Ցանկացած գնահատված պոտենցիալ φ, որը ճշգրիտ չի համընկնում իր իրական արժեքի հետ, նույնպես կհանգեցնի C-ի սխալ արժեքի՝ ավելի մեծ, քան անհրաժեշտ է: Բայց եթե սխալ ընտրված պոտենցիալ cp-ն դեռ կոպիտ մոտարկում է, ապա հզորությունը ՀԵՏկստացվի լավ ճշգրտությամբ, քանի որ C-ի սխալը երկրորդ կարգի արժեք է՝ համեմատած φ-ի սխալի հետ:

Ենթադրենք, որ ես չգիտեմ գլանաձեւ կոնդենսատորի հզորությունը։ Հետո, նրան ճանաչելու համար, ես կարող եմ օգտագործել այս սկզբունքը. Ես պարզապես կփորձարկեմ φ-ի տարբեր ֆունկցիաները որպես պոտենցիալ, մինչև հասնեմ ամենացածր արժեքին ՀԵՏ.Ասենք, օրինակ, ես ընտրել եմ մի ներուժ, որը համապատասխանում է հաստատուն դաշտին։ (Դուք, իհարկե, գիտեք, որ դաշտն այստեղ իրականում հաստատուն չէ, այն տատանվում է որպես 1/r) Եթե դաշտը հաստատուն է, դա նշանակում է, որ պոտենցիալը գծայինորեն կախված է հեռավորությունից: Որպեսզի հաղորդիչների վրա լարումը լինի ըստ պահանջի, φ ֆունկցիան պետք է ունենա ձև

Այս ֆունկցիան հավասար է Վ ժամը r=a,զրո ժամը r =b,և նրանց միջև կա հաստատուն թեքություն, որը հավասար է - Վ/(բ—Ա).Այսպիսով, ինտեգրալը որոշելու համար U*, պարզապես անհրաժեշտ է այս գրադիենտի քառակուսին բազմապատկել ε o /2-ով և ինտեգրել ամբողջ ծավալի վրա: Եկեք կատարենք այս հաշվարկը միավորի երկարության մխոցի համար: Ծավալի տարր շառավղով rհավասար է 2πrdr. Իրականացնելով ինտեգրումը, ես գտնում եմ, որ իմ առաջին թեստը տալիս է հետևյալ հզորությունը.

Այսպիսով, ես ստանում եմ հզորության բանաձև, որը թեև սխալ է, բայց ինչ-որ մոտավորություն է.

Իհարկե, դա տարբերվում է ճիշտ պատասխանից C=2pe 0 /ln (b/a),բայց ընդհանուր առմամբ դա այնքան էլ վատ չէ: Փորձենք այն համեմատել մի քանի արժեքների ճիշտ պատասխանի հետ բ/ա.Իմ հաշվարկած թվերը ներկայացված են հետևյալ աղյուսակում։

Նույնիսկ այն ժամանակ, երբ բ/ա=2(իսկ սա արդեն հանգեցնում է հաստատուն և գծային դաշտերի բավականին մեծ տարբերությունների), ես դեռ բավականին ընդունելի մոտարկում եմ ստանում։ Պատասխանը, իհարկե, ինչպես և սպասվում էր, մի փոքր չափազանց բարձր է։ Բայց եթե բարակ մետաղալար է տեղադրված մեծ մխոցի ներսում, ապա ամեն ինչ շատ ավելի վատ է թվում։ Հետո դաշտը շատ է փոխվում ու մշտական ​​դաշտով փոխարինելը ոչ մի լավ բանի չի բերում։ Երբ b/a = 100, մենք պատասխանը գերագնահատում ենք գրեթե երկու անգամ: Փոքրերի համար բ/աիրավիճակը շատ ավելի լավ է թվում. Հակառակ սահմանում, երբ հաղորդիչների միջև բացը շատ լայն չէ (ասենք, b/a = 1.1-ի համար), հաստատուն դաշտը շատ լավ մոտարկում է ստացվում, այն տալիս է արժեքը. ՀԵՏճշգրիտ մինչև տասներորդ տոկոսը:

Այժմ ես ձեզ կասեմ, թե ինչպես բարելավել այս հաշվարկը: (Գլանի պատասխանն, իհարկե, հետևյալն է. հայտնի,բայց նույն մեթոդն աշխատում է մի քանի այլ արտասովոր կոնդենսատորների ձևերի դեպքում, որոնց համար դուք կարող եք չգիտեք ճիշտ պատասխանը:) Հաջորդ քայլը ավելի լավ մոտարկում գտնելն է անհայտ իրական պոտենցիալի φ համար: Ենթադրենք, դուք կարող եք ստուգել հաստատունը գումարած φ ցուցիչը և այլն: Բայց ինչպե՞ս իմանաք, որ ստացել եք լավագույն մոտավորությունը, եթե չգիտեք ճշմարիտ φ: Պատասխան.Հաշվիր այն ՀԵՏ;որքան ցածր է, այնքան ավելի մոտ է ճշմարտությանը: Եկեք փորձարկենք այս գաղափարը: Թող պոտենցիալը լինի ոչ թե գծային, այլ, ասենք, քառակուսային r-ում, իսկ էլեկտրական դաշտը ոչ հաստատուն, այլ գծային։ Առավելագույնը ընդհանուրքառակուսի ձև, որը վերածվում է φ=O-ի, երբ r=բիսկ φ=F ժամը r=a,սա է:

որտեղ α-ն հաստատուն թիվ է: Այս բանաձեւը մի փոքր ավելի բարդ է, քան նախորդը։ Այն ներառում է և՛ քառակուսի անդամ, և՛ գծային: Դրանից դաշտ ստանալը շատ հեշտ է։ Դա հավասար է պարզի

Այժմ սա պետք է քառակուսի և ինտեգրվի ծավալի վրա: Բայց մի րոպե սպասեք: Ինչ պետք է վերցնեմ α-ի համար: Ես կարող եմ f-ը պարաբոլա համարել, բայց ո՞րը: Ահա թե ինչ կանեմ՝ հաշվարկել հզորությունը ժամը կամայական α.ես կստանամ

Սա մի փոքր շփոթեցնող է թվում, բայց դաշտի քառակուսին ինտեգրվելուց հետո այդպես է ստացվում: Հիմա ես կարող եմ ինքս ընտրել։ Ես գիտեմ, որ ճշմարտությունն ավելի ցածր է, քան այն ամենը, ինչ ես պատրաստվում եմ հաշվարկել: Անկախ նրանից, թե ինչ եմ դնում a-ի փոխարեն, պատասխանը դեռ շատ մեծ է լինելու։ Բայց եթե ես շարունակեմ իմ խաղը α-ի հետ և փորձեմ հասնել հնարավոր ամենացածր արժեքին ՀԵՏ,ապա այս ամենացածր արժեքը ավելի մոտ կլինի ճշմարտությանը, քան ցանկացած այլ արժեք: Հետևաբար, ես հիմա պետք է ընտրեմ α, որպեսզի արժեքը ՀԵՏհասել է իր նվազագույնին. Անդրադառնալով սովորական դիֆերենցիալ հաշվարկին, ես համոզված եմ, որ նվազագույնը ՀԵՏկլինի, երբ α =— 2 բ/(բ+ա). Փոխարինելով այս արժեքը բանաձևի մեջ, ես ստանում եմ ամենափոքր հզորությունը

Ես հասկացա, թե ինչ է տալիս այս բանաձեւը ՀԵՏտարբեր արժեքներով բ/ա.Ես անվանեցի այս թվերը ՀԵՏ(քառակուսի): Ահա մի աղյուսակ, որը համեմատում է ՀԵՏ(քառակուսի) հետ ՀԵՏ(ճիշտ).

Օրինակ, երբ շառավիղի հարաբերակցությունը 2:1 է, ես ստանում եմ 1,444: Սա շատ լավ մոտարկում է ճիշտ պատասխանին՝ 1,4423: Նույնիսկ մեծերով Յամոտարկումը մնում է բավականին լավ՝ շատ ավելի լավ, քան առաջին մոտարկումը: Այն մնում է տանելի (գերագնահատված է ընդամենը 10%) նույնիսկ b/a = 10:1 դեպքում: Մեծ անհամապատասխանություն տեղի է ունենում միայն 100:1 հարաբերակցությամբ: Ես ստանում եմ. ՀԵՏհավասար է 0,346-ի՝ 0,267-ի փոխարեն: Մյուս կողմից, 1,5 շառավղով հարաբերակցության համար համաձայնությունը գերազանց է, և համար բ/ա=1.1պատասխանը 10.492065 է՝ սպասված 10.492070-ի փոխարեն։ Այնտեղ, որտեղ դուք կակնկալեիք լավ պատասխան, շատ-շատ լավ է ստացվում։

Ես բերել եմ այս բոլոր օրինակները, նախ՝ ցույց տալու համար նվազագույն գործողության սկզբունքի և ընդհանրապես նվազագույնի բոլոր սկզբունքների տեսական արժեքը, և երկրորդ՝ ձեզ ցույց տալու դրանց գործնական օգտակարությունը, և ամենևին էլ՝ հնարավորությունը հաշվարկելու համար։ որ մենք արդեն ունենք, շատ լավ գիտենք։ Ցանկացած այլ ձևի համար կարող եք փորձել մոտավոր դաշտ մի քանի անհայտ պարամետրով (ինչպես α-ն) և համապատասխանեցնել դրանք նվազագույնի: Դուք կստանաք գերազանց թվային արդյունքներ խնդիրների վերաբերյալ, որոնք այլ կերպ հնարավոր չէ լուծել:

Նրանք ենթարկվում են դրան, և, հետևաբար, այս սկզբունքը ժամանակակից ֆիզիկայի առանցքային դրույթներից մեկն է։ Նրա օգնությամբ ստացված շարժման հավասարումները կոչվում են Էյլեր-Լագրանժի հավասարումներ։

Սկզբունքի առաջին ձևակերպումը տվել է Պ.Մաուպերտուիսը տարում՝ անմիջապես մատնանշելով դրա ունիվերսալ բնույթը՝ այն կիրառելի համարելով օպտիկայի և մեխանիկայի համար։ Այս սկզբունքից նա դուրս է բերել լույսի արտացոլման և բեկման օրենքները։

Պատմություն

Մաուպերտուիսը եկել է այս սկզբունքին այն զգացումից, որ Տիեզերքի կատարելությունը պահանջում է որոշակի տնտեսություն բնության մեջ և հակասում է էներգիայի ցանկացած անօգուտ ծախսմանը: Բնական շարժումը պետք է լինի այնպիսին, որ որոշակի քանակություն լինի նվազագույն: Նրան մնում էր միայն գտնել այս արժեքը, որը նա շարունակեց անել։ Դա համակարգի ներսում շարժման տևողության (ժամանակի) արտադրյալն էր երկու անգամ ավելի մեծ արժեքով, որն այժմ մենք անվանում ենք համակարգի կինետիկ էներգիա:

Էյլեր (in «Réflexions sur quelques loix générales de la nature», 1748) ընդունում է գործողության նվազագույն քանակի սկզբունքը՝ գործողությունն անվանելով «ջանք»։ Դրա արտահայտությունը ստատիկայում համապատասխանում է նրան, ինչ մենք հիմա կանվանեինք պոտենցիալ էներգիա, այնպես որ ստատիկայում դրա նվազագույն գործողության մասին հայտարարությունը համարժեք է հավասարակշռության կոնֆիգուրացիայի համար նվազագույն պոտենցիալ էներգիայի պայմանին:

Դասական մեխանիկայի մեջ

Նվազագույն գործողության սկզբունքը ծառայում է որպես մեխանիկայի Լագրանժյան և Համիլտոնյան ձևակերպումների հիմնարար և ստանդարտ հիմք:

Նախ, եկեք նայենք շինարարությանը այսպես. Լագրանժյան մեխանիկա. Օգտագործելով ազատության մեկ աստիճան ունեցող ֆիզիկական համակարգի օրինակը՝ հիշենք, որ գործողությունը ֆունկցիոնալ է (ընդհանրացված) կոորդինատների նկատմամբ (ազատության մեկ աստիճանի դեպքում՝ մեկ կոորդինատ), այսինքն՝ այն արտահայտվում է միջոցով. այնպիսին, որ ֆունկցիայի յուրաքանչյուր պատկերավոր տարբերակ կապված է որոշակի թվի հետ՝ գործողության (այս իմաստով, կարող ենք ասել, որ գործողությունը որպես ֆունկցիոնալ կանոն է, որը թույլ է տալիս ցանկացած ֆունկցիայի հաշվարկել միանգամայն կոնկրետ թիվ, որը նաև կոչվում է. գործողություն): Գործողությունը նման է.

որտեղ է համակարգի Լագրանժականը, կախված ընդհանրացված կոորդինատից, նրա առաջին ածանցյալը ժամանակի նկատմամբ, և նաև, հնարավոր է, հստակ ժամանակին: Եթե ​​համակարգն ունի ավելի մեծ թվով ազատության աստիճաններ, ապա Լագրանժականը կախված է ավելի մեծ թվով ընդհանրացված կոորդինատներից և դրանց առաջին ածանցյալներից՝ կապված ժամանակի հետ։ Այսպիսով, գործողությունը սկալյար ֆունկցիոնալ է, կախված մարմնի հետագծից:

Այն փաստը, որ գործողությունը սկալյար է, հեշտացնում է այն գրել ցանկացած ընդհանրացված կոորդինատներով, գլխավորն այն է, որ համակարգի դիրքը (կոնֆիգուրացիա) միանշանակ բնութագրվում է դրանցով (օրինակ, դեկարտյան կոորդինատների փոխարեն, դրանք կարող են լինել բևեռային. կոորդինատները, համակարգի կետերի միջև եղած հեռավորությունները, անկյունները կամ դրանց ֆունկցիաները և այլն: դ.):

Գործողությունը կարող է հաշվարկվել միանգամայն կամայական հետագծի համար, անկախ նրանից, թե որքան «վայրի» և «անբնական» լինի: Այնուամենայնիվ, դասական մեխանիկայի մեջ, հնարավոր հետագծերի ամբողջ շարքում կա միայն մեկը, որի երկայնքով մարմինը իրականում կգնա: Անշարժ գործողության սկզբունքը ճշգրիտ պատասխան է տալիս այն հարցին, թե իրականում ինչպես է շարժվելու մարմինը.

Սա նշանակում է, որ եթե տրված է համակարգի Լագրանժը, ապա, օգտագործելով տատանումների հաշվարկը, մենք կարող ենք ճշգրիտ որոշել, թե մարմինը ինչպես է շարժվելու՝ սկզբում ստանալով շարժման հավասարումները՝ Էյլեր-Լագրանժի հավասարումները, այնուհետև լուծելով դրանք: Սա թույլ է տալիս ոչ միայն լրջորեն ընդհանրացնել մեխանիկայի ձևակերպումը, այլև ընտրել ամենահարմար կոորդինատները յուրաքանչյուր կոնկրետ խնդրի համար, չսահմանափակվելով դեկարտյաններով, ինչը կարող է շատ օգտակար լինել ամենապարզ և հեշտ լուծվող հավասարումները ստանալու համար:

որտեղ է այս համակարգի Համիլթոնի գործառույթը. - (ընդհանրացված) կոորդինատներ, - զուգակցված (ընդհանրացված) իմպուլսներ, որոնք միասին բնութագրում են ժամանակի յուրաքանչյուր պահի համակարգի դինամիկ վիճակը և յուրաքանչյուրը ժամանակի ֆունկցիա լինելով՝ այդպիսով բնութագրելով համակարգի էվոլյուցիան (շարժումը): Այս դեպքում Համիլթոնի կանոնական հավասարումների տեսքով համակարգի շարժման հավասարումները ստանալու համար անհրաժեշտ է բոլորի համար ինքնուրույն փոփոխել այս կերպ գրված գործողությունը և .

Պետք է նշել, որ եթե խնդրի պայմաններից սկզբունքորեն հնարավոր է գտնել շարժման օրենքը, ապա դա ինքնաբերաբար Ոչնշանակում է, որ հնարավոր է կառուցել մի ֆունկցիոնալ, որն ընդունում է անշարժ արժեք իրական շարժման ժամանակ: Օրինակ՝ էլեկտրական լիցքերի և մոնոպոլների՝ մագնիսական լիցքերի համատեղ շարժումը էլեկտրամագնիսական դաշտում։ Նրանց շարժման հավասարումները չեն կարող ստացվել անշարժ գործողության սկզբունքից։ Նմանապես, որոշ Համիլտոնյան համակարգեր ունեն շարժման հավասարումներ, որոնք չեն կարող բխվել այս սկզբունքից:

Օրինակներ

Չնչին օրինակները օգնում են գնահատել գործառնական սկզբունքի օգտագործումը Էյլեր-Լագրանժի հավասարումների միջոցով: Ազատ մասնիկ (զանգված մև արագություն v) Էվկլիդեսյան տարածության մեջ շարժվում է ուղիղ գծով։ Օգտագործելով Էյլեր-Լագրանժի հավասարումները, դա կարելի է ցույց տալ բևեռային կոորդինատներով հետևյալ կերպ. Պոտենցիալի բացակայության դեպքում Լագրանժի ֆունկցիան պարզապես հավասար է կինետիկ էներգիային

ուղղանկյուն կոորդինատային համակարգում:

Բևեռային կոորդինատներում կինետիկ էներգիան և, հետևաբար, Լագրանժի ֆունկցիան դառնում է

Հավասարումների շառավղային և անկյունային բաղադրիչները համապատասխանաբար դառնում են.

Լուծելով այս երկու հավասարումները

Ահա բոլոր x(t) հետագծերի վրա անսահման բազմակի ֆունկցիոնալ ինտեգրման պայմանական նշում և Պլանկի հաստատունն է: Մենք ընդգծում ենք, որ, սկզբունքորեն, էքսպոնենցիալում գործողությունը հայտնվում է (կամ կարող է հայտնվել) ինքն իրեն, երբ ուսումնասիրում է էվոլյուցիոն օպերատորը քվանտային մեխանիկայի մեջ, բայց համակարգերի համար, որոնք ունեն ճշգրիտ դասական (ոչ քվանտային) անալոգային, դա ճիշտ հավասար է սովորականին: դասական գործողություն.

Այս արտահայտության մաթեմատիկական վերլուծությունը դասական սահմանում - բավականաչափ մեծ, այսինքն՝ երևակայական էքսպոնենցիալ շատ արագ տատանումների համար, ցույց է տալիս, որ այս ինտեգրալում բոլոր հնարավոր հետագծերի ճնշող մեծամասնությունը միմյանց չեղարկում են սահմանում (ձևականորեն): Գրեթե ցանկացած ճանապարհի համար կա մի ճանապարհ, որի վրա փուլային հերթափոխը կլինի ճիշտ հակառակը, և դրանք կավելանան մինչև զրոյական ներդրում: Չեն կրճատվում միայն այն հետագծերը, որոնց գործողությունը մոտ է ծայրահեղ արժեքին (համակարգերի մեծ մասի համար՝ նվազագույնին): Սա զուտ մաթեմատիկական փաստ է բարդ փոփոխականի ֆունկցիաների տեսությունից. Օրինակ, դրա վրա հիմնված է ստացիոնար փուլային մեթոդը:

Արդյունքում, մասնիկը, լիովին համաձայնելով քվանտային մեխանիկայի օրենքների հետ, միաժամանակ շարժվում է բոլոր հետագծերով, բայց նորմալ պայմաններում միայն անշարժ (այսինքն՝ դասական) մոտ հետագծերը նպաստում են դիտարկվող արժեքներին։ Քանի որ քվանտային մեխանիկա վերածվում է դասական մեխանիկայի բարձր էներգիաների սահմաններում, մենք կարող ենք ենթադրել, որ սա Գործողության կայունության դասական սկզբունքի քվանտային մեխանիկական ածանցում.

Քվանտային դաշտի տեսության մեջ

Դաշտի քվանտային տեսության մեջ հաջողությամբ կիրառվում է նաև անշարժ գործողության սկզբունքը։ Լագրանժյան խտությունն այստեղ ներառում է համապատասխան քվանտային դաշտերի օպերատորները։ Թեև այստեղ ավելի ճիշտ է ըստ էության (բացառությամբ դասական սահմանի և մասամբ քվազի-դասականների) խոսել ոչ թե գործողության կայունության սկզբունքի մասին, այլ Ֆեյնմանի ինտեգրման մասին հետագծերի երկայնքով այս դաշտերի կոնֆիգուրացիայի կամ փուլային տարածության մեջ. հենց նոր նշված Լագրանժյան խտությունը։

Հետագա ընդհանրացումներ

Ավելի լայնորեն, գործողությունը հասկացվում է որպես ֆունկցիոնալ, որը սահմանում է քարտեզագրում կոնֆիգուրացիայի տարածությունից մինչև իրական թվերի բազմություն և, ընդհանուր առմամբ, պարտադիր չէ, որ այն լինի ինտեգրալ, քանի որ ոչ տեղական գործողություններ սկզբունքորեն հնարավոր են, համենայն դեպս: տեսականորեն։ Ավելին, կոնֆիգուրացիայի տարածքը պարտադիր չէ, որ ֆունկցիայի տարածք լինի, քանի որ այն կարող է ունենալ ոչ փոխադարձ երկրաչափություն:

Նրանք ենթարկվում են դրան, և, հետևաբար, այս սկզբունքը ժամանակակից ֆիզիկայի առանցքային դրույթներից մեկն է։ Նրա օգնությամբ ստացված շարժման հավասարումները կոչվում են Էյլեր-Լագրանժի հավասարումներ։

Սկզբունքի առաջին ձևակերպումը տվել է Պ.Մաուպերտուիսը տարում՝ անմիջապես մատնանշելով դրա ունիվերսալ բնույթը՝ այն կիրառելի համարելով օպտիկայի և մեխանիկայի համար։ Այս սկզբունքից նա դուրս է բերել լույսի արտացոլման և բեկման օրենքները։

Պատմություն

Մաուպերտուիսը եկել է այս սկզբունքին այն զգացումից, որ Տիեզերքի կատարելությունը պահանջում է որոշակի տնտեսություն բնության մեջ և հակասում է էներգիայի ցանկացած անօգուտ ծախսմանը: Բնական շարժումը պետք է լինի այնպիսին, որ որոշակի քանակություն լինի նվազագույն: Նրան մնում էր միայն գտնել այս արժեքը, որը նա շարունակեց անել։ Դա համակարգի ներսում շարժման տևողության (ժամանակի) արտադրյալն էր երկու անգամ ավելի մեծ արժեքով, որն այժմ մենք անվանում ենք համակարգի կինետիկ էներգիա:

Էյլեր (in «Réflexions sur quelques loix générales de la nature», 1748) ընդունում է գործողության նվազագույն քանակի սկզբունքը՝ գործողությունն անվանելով «ջանք»։ Դրա արտահայտությունը ստատիկայում համապատասխանում է նրան, ինչ մենք հիմա կանվանեինք պոտենցիալ էներգիա, այնպես որ ստատիկայում դրա նվազագույն գործողության մասին հայտարարությունը համարժեք է հավասարակշռության կոնֆիգուրացիայի համար նվազագույն պոտենցիալ էներգիայի պայմանին:

Դասական մեխանիկայի մեջ

Նվազագույն գործողության սկզբունքը ծառայում է որպես մեխանիկայի Լագրանժյան և Համիլտոնյան ձևակերպումների հիմնարար և ստանդարտ հիմք:

Նախ, եկեք նայենք շինարարությանը այսպես. Լագրանժյան մեխանիկա. Օգտագործելով ազատության մեկ աստիճան ունեցող ֆիզիկական համակարգի օրինակը՝ հիշենք, որ գործողությունը ֆունկցիոնալ է (ընդհանրացված) կոորդինատների նկատմամբ (ազատության մեկ աստիճանի դեպքում՝ մեկ կոորդինատ), այսինքն՝ այն արտահայտվում է միջոցով. այնպիսին, որ ֆունկցիայի յուրաքանչյուր պատկերավոր տարբերակ կապված է որոշակի թվի հետ՝ գործողության (այս իմաստով, կարող ենք ասել, որ գործողությունը որպես ֆունկցիոնալ կանոն է, որը թույլ է տալիս ցանկացած ֆունկցիայի հաշվարկել միանգամայն կոնկրետ թիվ, որը նաև կոչվում է. գործողություն): Գործողությունը նման է.

որտեղ է համակարգի Լագրանժականը, կախված ընդհանրացված կոորդինատից, նրա առաջին ածանցյալը ժամանակի նկատմամբ, և նաև, հնարավոր է, հստակ ժամանակին: Եթե ​​համակարգն ունի ավելի մեծ թվով ազատության աստիճաններ, ապա Լագրանժականը կախված է ավելի մեծ թվով ընդհանրացված կոորդինատներից և դրանց առաջին ածանցյալներից՝ կապված ժամանակի հետ։ Այսպիսով, գործողությունը սկալյար ֆունկցիոնալ է, կախված մարմնի հետագծից:

Այն փաստը, որ գործողությունը սկալյար է, հեշտացնում է այն գրել ցանկացած ընդհանրացված կոորդինատներով, գլխավորն այն է, որ համակարգի դիրքը (կոնֆիգուրացիա) միանշանակ բնութագրվում է դրանցով (օրինակ, դեկարտյան կոորդինատների փոխարեն, դրանք կարող են լինել բևեռային. կոորդինատները, համակարգի կետերի միջև եղած հեռավորությունները, անկյունները կամ դրանց ֆունկցիաները և այլն: դ.):

Գործողությունը կարող է հաշվարկվել միանգամայն կամայական հետագծի համար, անկախ նրանից, թե որքան «վայրի» և «անբնական» լինի: Այնուամենայնիվ, դասական մեխանիկայի մեջ, հնարավոր հետագծերի ամբողջ շարքում կա միայն մեկը, որի երկայնքով մարմինը իրականում կգնա: Անշարժ գործողության սկզբունքը ճշգրիտ պատասխան է տալիս այն հարցին, թե իրականում ինչպես է շարժվելու մարմինը.

Սա նշանակում է, որ եթե տրված է համակարգի Լագրանժը, ապա, օգտագործելով տատանումների հաշվարկը, մենք կարող ենք ճշգրիտ որոշել, թե մարմինը ինչպես է շարժվելու՝ սկզբում ստանալով շարժման հավասարումները՝ Էյլեր-Լագրանժի հավասարումները, այնուհետև լուծելով դրանք: Սա թույլ է տալիս ոչ միայն լրջորեն ընդհանրացնել մեխանիկայի ձևակերպումը, այլև ընտրել ամենահարմար կոորդինատները յուրաքանչյուր կոնկրետ խնդրի համար, չսահմանափակվելով դեկարտյաններով, ինչը կարող է շատ օգտակար լինել ամենապարզ և հեշտ լուծվող հավասարումները ստանալու համար:

որտեղ է այս համակարգի Համիլթոնի գործառույթը. - (ընդհանրացված) կոորդինատներ, - զուգակցված (ընդհանրացված) իմպուլսներ, որոնք միասին բնութագրում են ժամանակի յուրաքանչյուր պահի համակարգի դինամիկ վիճակը և յուրաքանչյուրը ժամանակի ֆունկցիա լինելով՝ այդպիսով բնութագրելով համակարգի էվոլյուցիան (շարժումը): Այս դեպքում Համիլթոնի կանոնական հավասարումների տեսքով համակարգի շարժման հավասարումները ստանալու համար անհրաժեշտ է բոլորի համար ինքնուրույն փոփոխել այս կերպ գրված գործողությունը և .

Պետք է նշել, որ եթե խնդրի պայմաններից սկզբունքորեն հնարավոր է գտնել շարժման օրենքը, ապա դա ինքնաբերաբար Ոչնշանակում է, որ հնարավոր է կառուցել մի ֆունկցիոնալ, որն ընդունում է անշարժ արժեք իրական շարժման ժամանակ: Օրինակ՝ էլեկտրական լիցքերի և մոնոպոլների՝ մագնիսական լիցքերի համատեղ շարժումը էլեկտրամագնիսական դաշտում։ Նրանց շարժման հավասարումները չեն կարող ստացվել անշարժ գործողության սկզբունքից։ Նմանապես, որոշ Համիլտոնյան համակարգեր ունեն շարժման հավասարումներ, որոնք չեն կարող բխվել այս սկզբունքից:

Օրինակներ

Չնչին օրինակները օգնում են գնահատել գործառնական սկզբունքի օգտագործումը Էյլեր-Լագրանժի հավասարումների միջոցով: Ազատ մասնիկ (զանգված մև արագություն v) Էվկլիդեսյան տարածության մեջ շարժվում է ուղիղ գծով։ Օգտագործելով Էյլեր-Լագրանժի հավասարումները, դա կարելի է ցույց տալ բևեռային կոորդինատներով հետևյալ կերպ. Պոտենցիալի բացակայության դեպքում Լագրանժի ֆունկցիան պարզապես հավասար է կինետիկ էներգիային

ուղղանկյուն կոորդինատային համակարգում:

Բևեռային կոորդինատներում կինետիկ էներգիան և, հետևաբար, Լագրանժի ֆունկցիան դառնում է

Հավասարումների շառավղային և անկյունային բաղադրիչները համապատասխանաբար դառնում են.

Լուծելով այս երկու հավասարումները

Ահա բոլոր x(t) հետագծերի վրա անսահման բազմակի ֆունկցիոնալ ինտեգրման պայմանական նշում և Պլանկի հաստատունն է: Մենք ընդգծում ենք, որ, սկզբունքորեն, էքսպոնենցիալում գործողությունը հայտնվում է (կամ կարող է հայտնվել) ինքն իրեն, երբ ուսումնասիրում է էվոլյուցիոն օպերատորը քվանտային մեխանիկայի մեջ, բայց համակարգերի համար, որոնք ունեն ճշգրիտ դասական (ոչ քվանտային) անալոգային, դա ճիշտ հավասար է սովորականին: դասական գործողություն.

Այս արտահայտության մաթեմատիկական վերլուծությունը դասական սահմանում - բավականաչափ մեծ, այսինքն՝ երևակայական էքսպոնենցիալ շատ արագ տատանումների համար, ցույց է տալիս, որ այս ինտեգրալում բոլոր հնարավոր հետագծերի ճնշող մեծամասնությունը միմյանց չեղարկում են սահմանում (ձևականորեն): Գրեթե ցանկացած ճանապարհի համար կա մի ճանապարհ, որի վրա փուլային հերթափոխը կլինի ճիշտ հակառակը, և դրանք կավելանան մինչև զրոյական ներդրում: Չեն կրճատվում միայն այն հետագծերը, որոնց գործողությունը մոտ է ծայրահեղ արժեքին (համակարգերի մեծ մասի համար՝ նվազագույնին): Սա զուտ մաթեմատիկական փաստ է բարդ փոփոխականի ֆունկցիաների տեսությունից. Օրինակ, դրա վրա հիմնված է ստացիոնար փուլային մեթոդը:

Արդյունքում, մասնիկը, լիովին համաձայնելով քվանտային մեխանիկայի օրենքների հետ, միաժամանակ շարժվում է բոլոր հետագծերով, բայց նորմալ պայմաններում միայն անշարժ (այսինքն՝ դասական) մոտ հետագծերը նպաստում են դիտարկվող արժեքներին։ Քանի որ քվանտային մեխանիկա վերածվում է դասական մեխանիկայի բարձր էներգիաների սահմաններում, մենք կարող ենք ենթադրել, որ սա Գործողության կայունության դասական սկզբունքի քվանտային մեխանիկական ածանցում.

Քվանտային դաշտի տեսության մեջ

Դաշտի քվանտային տեսության մեջ հաջողությամբ կիրառվում է նաև անշարժ գործողության սկզբունքը։ Լագրանժյան խտությունն այստեղ ներառում է համապատասխան քվանտային դաշտերի օպերատորները։ Թեև այստեղ ավելի ճիշտ է ըստ էության (բացառությամբ դասական սահմանի և մասամբ քվազի-դասականների) խոսել ոչ թե գործողության կայունության սկզբունքի մասին, այլ Ֆեյնմանի ինտեգրման մասին հետագծերի երկայնքով այս դաշտերի կոնֆիգուրացիայի կամ փուլային տարածության մեջ. հենց նոր նշված Լագրանժյան խտությունը։

Հետագա ընդհանրացումներ

Ավելի լայնորեն, գործողությունը հասկացվում է որպես ֆունկցիոնալ, որը սահմանում է քարտեզագրում կոնֆիգուրացիայի տարածությունից մինչև իրական թվերի բազմություն և, ընդհանուր առմամբ, պարտադիր չէ, որ այն լինի ինտեգրալ, քանի որ ոչ տեղական գործողություններ սկզբունքորեն հնարավոր են, համենայն դեպս: տեսականորեն։ Ավելին, կոնֆիգուրացիայի տարածքը պարտադիր չէ, որ ֆունկցիայի տարածք լինի, քանի որ այն կարող է ունենալ ոչ փոխադարձ երկրաչափություն:

Նվազագույն գործողության սկզբունքը, որն առաջին անգամ ձևակերպվել է հենց Ջակոբիի կողմից, նման է Համիլթոնի սկզբունքին, բայց ավելի քիչ ընդհանուր և ավելի դժվար ապացուցելի: Այս սկզբունքը կիրառելի է միայն այն դեպքում, երբ միացումներն ու ուժային ֆունկցիան կախված չեն ժամանակից, և երբ, հետևաբար, կա կենդանի ուժի ինտեգրալ։

Այս ինտեգրալն ունի ձև.

Համիլթոնի վերը նշված սկզբունքը նշում է, որ ինտեգրալի փոփոխությունը

հավասար է զրոյի՝ իրական շարժման ցանկացած այլ անսահման մոտ շարժման անցնելիս, որը նույն ժամանակահատվածում համակարգը տեղափոխում է նույն սկզբնական դիրքից նույն վերջնական դիրքը։

Յակոբիի սկզբունքը, ընդհակառակը, արտահայտում է շարժման հատկություն, որը կախված չէ ժամանակից։ Յակոբին համարում է ինտեգրալը

գործողության որոշում. Նրա հաստատած սկզբունքն ասում է, որ այս ինտեգրալի փոփոխությունը զրո է, երբ մենք համեմատում ենք համակարգի իրական շարժումը ցանկացած այլ անսահման մոտ շարժման հետ, որը համակարգը տանում է նույն սկզբնական դիրքից մինչև նույն վերջնական դիրքը: Այս դեպքում մենք ուշադրություն չենք դարձնում ծախսված ժամանակաշրջանին, այլ դիտարկում ենք (1) հավասարումը, այսինքն՝ աշխատուժի հավասարումը h հաստատունի նույն արժեքով, ինչ իրական շարժման դեպքում:

Ծայրահեղության համար այս անհրաժեշտ պայմանը, ընդհանուր առմամբ, հանգեցնում է ինտեգրալի նվազագույնի (2), այստեղից էլ կոչվում է նվազագույն գործողության սկզբունք: Նվազագույն պայմանը թվում է ամենաբնականը, քանի որ T-ի արժեքը ըստ էության դրական է, և հետևաբար ինտեգրալը (2) պետք է անպայման ունենա նվազագույնը: Նվազագույնի առկայությունը կարող է խստորեն ապացուցվել, եթե միայն ժամանակային ժամանակահատվածը բավականաչափ փոքր է: Այս դիրքորոշման ապացույցը կարելի է գտնել Դարբուի մակերեւութային տեսության հայտնի դասընթացում։ Մենք, սակայն, դա այստեղ չենք ներկայացնի և կսահմանափակվենք պայմանը բխելով

432. Նվազագույն գործողության սկզբունքի ապացույց.

Փաստացի հաշվարկում մենք հանդիպում ենք մեկ դժվարության, որը չկա Համիլթոնի թեորեմի ապացուցման մեջ։ t փոփոխականն այլևս չի մնում տատանումներից անկախ. հետևաբար q i և q տատանումները: կապված են t-ի փոփոխության հետ բարդ հարաբերությունով, որը բխում է (1) հավասարումից: Այս դժվարությունը շրջանցելու ամենապարզ միջոցը անկախ փոփոխականը փոխելն է, ընտրելով մեկը, որի արժեքներն ընկնում են ժամանակից կախված մշտական ​​սահմանների միջև: Թող k-ն լինի նոր անկախ փոփոխական, որի սահմանները ենթադրվում են t-ից անկախ։ Համակարգը տեղափոխելիս պարամետրերը և t-ը կլինեն այս փոփոխականի գործառույթները

Թող պարզ թվերով q տառերը նշանակեն q պարամետրերի ածանցյալները ժամանակի նկատմամբ:

Քանի որ կապերը, ըստ ենթադրության, կախված չեն ժամանակից, ապա դեկարտյան կոորդինատները x, y, z-ն ժամանակ չպարունակող q-ի ֆունկցիաներ են։ Հետևաբար, դրանց ածանցյալները կլինեն q-ի գծային միատարր ֆունկցիաներ, իսկ 7-ը՝ q-ի միատարր քառակուսի ձևը, որի գործակիցները q-ի ֆունկցիաներն են։ Մենք ունենք

q-ի ածանցյալները ժամանակի նկատմամբ տարբերելու համար փակագծերի միջոցով նշում ենք (q) q-ի ածանցյալները, որոնք վերցված են և դրվում են դրան համապատասխան.

ապա կունենանք

իսկ ինտեգրալը (2), որն արտահայտված է նոր անկախ փոփոխական A-ի միջոցով, կունենա ձև.

Ածանցյալը կարելի է վերացնել՝ օգտագործելով կենդանի ուժի թեորեմը։ Իրոք, աշխատուժի ինտեգրալը կլինի

Այս արտահայտությունը փոխարինելով բանաձևով, մենք (2) ինտեգրալը վերածում ենք ձևի

Այսպիսով, գործողությունը սահմանող ինտեգրալը ստացավ իր վերջնական ձևը (3): Ինտեգրանդ ֆունկցիան մեծությունների քառակուսի ձևի քառակուսի արմատն է

Եկեք ցույց տանք, որ (3) ինտեգրալի էքստրեմալների դիֆերենցիալ հավասարումները հենց Լագրանժի հավասարումներն են: Էքստրեմալների հավասարումները, որոնք հիմնված են տատանումների հաշվարկի ընդհանուր բանաձևերի վրա, կլինեն.

Բազմապատկենք հավասարումները 2-ով և կատարենք մասնակի տարբերակումներ՝ հաշվի առնելով, որ այն չի պարունակում, ապա ստանում ենք, եթե ինդեքս չգրենք.

Սրանք էքստրեմալների հավասարումներ են, որոնք արտահայտված են անկախ փոփոխականով: Այժմ խնդիրն է վերադառնալ անկախ փոփոխականին:

Քանի որ Γ-ը երկրորդ աստիճանի միատարր ֆունկցիա է և առաջին աստիճանի միատարր ֆունկցիա է, մենք ունենք

Մյուս կողմից, կենդանի ուժի թեորեմը կարող է կիրառվել էքստրեմալների հավասարումների ածանցյալների գործոնների վրա, ինչը հանգեցնում է, ինչպես տեսանք վերևում, փոխարինման.

Բոլոր փոխարինումների արդյունքում էքստրեմալների հավասարումները վերածվում են ձևի

Այսպիսով, մենք հասանք Լագրանժի հավասարումների:

433. Այն դեպքը, երբ չկան շարժիչ ուժեր.

Այն դեպքում, երբ չկան շարժիչ ուժեր, գոյություն ունի կենդանի ուժի հավասարում և ունենք

Ինտեգրալի նվազագույն լինելու պայմանն այս դեպքում այն ​​է, որ -10-ի համապատասխան արժեքը պետք է լինի ամենափոքրը։ Այսպիսով, երբ չկան շարժիչ ուժեր, ապա այն բոլոր շարժումների մեջ, որոնցում կենդանի ուժը պահպանում է նույն արժեքը, իրական շարժումն այն է, որը համակարգն իր սկզբնական դիրքից տեղափոխում է վերջնական դիրք ամենակարճ ժամանակում:

Եթե ​​համակարգը կրճատվում է մինչև մեկ կետ, որը շարժվում է անշարժ մակերևույթի վրա, ապա իրական շարժումը, մակերևույթի բոլոր շարժումներից, որոնք տեղի են ունենում նույն արագությամբ, այն շարժումն է, որի դեպքում կետը իր սկզբնական դիրքից տեղափոխվում է վերջնական դիրք: ամենակարճ

ժամանակային ընդմիջում. Այլ կերպ ասած, կետը մակերեսի վրա նկարագրում է իր երկու դիրքերի միջև ամենակարճ գիծը, այսինքն՝ գեոդեզիական գիծը:

434. Ծանոթագրություն.

Նվազագույն գործողության սկզբունքը ենթադրում է, որ համակարգն ունի ազատության մի քանի աստիճան, քանի որ եթե լիներ ազատության միայն մեկ աստիճան, ապա մեկ հավասարումը բավարար կլիներ շարժումը որոշելու համար: Քանի որ շարժումը այս դեպքում կարող է ամբողջությամբ որոշվել կենդանի ուժի հավասարմամբ, ապա իրական շարժումը կլինի միակը, որը բավարարում է այս հավասարումը, և, հետևաբար, չի կարող համեմատվել որևէ այլ շարժման հետ:


ՆՈՔԻ ԱՐԴՅՈՒՆԱՎԵՏ ՍԿԶԲՈՒՆՔ

Մեխանիկայի վարիացիոն սկզբունքներից մեկը, ըստ Կրոմի, միմյանց հետ համեմատած մեխանիկական շարժումների տվյալ դասի համար։ համակարգ, վավերականն այն է, որի համար ֆիզիկական. չափը, կոչ գործողություն, ունի ամենափոքր (ավելի ճիշտ՝ անշարժ) արժեքը։ Սովորաբար N. d. p.-ն օգտագործվում է երկու ձևերից մեկով.

ա) N. d. p.-ի տեսքով Համիլթոն - Օստրոգրադսկին հաստատում է, որ համակարգի բոլոր կինեմատիկորեն հնարավոր շարժումներից մեկ կոնֆիգուրացիայից մյուսը (առաջինին մոտ), որը կատարվել է նույն ժամանակահատվածում, վավերականն այն է, որի համար. Համիլտոնյան գործողությունը S կլինի ամենափոքրը: Մաթեմատիկա. N. d.p.-ի արտահայտությունն այս դեպքում ունի ձև՝ dS = 0, որտեղ d-ն թերի (իզոխրոն) փոփոխության խորհրդանիշն է (այսինքն, ի տարբերություն ամբողջական տատանումների, ժամանակը դրանում չի տատանվում):

բ) N. d. p. Maupertuis-ի ձևով - Լագրանժը հաստատում է, որ համակարգի բոլոր կինեմատիկորեն հնարավոր շարժումների շարքում մի կոնֆիգուրացիայից մյուսը մոտ, որը կատարվում է համակարգի ընդհանուր էներգիայի նույն արժեքը պահպանելով, վավերականն այն է. համար - Հետևաբար, Լագրանժի գործողությունը W կլինի ամենափոքրը: Մաթեմատիկա. N. d.p.-ի արտահայտությունն այս դեպքում ունի DW = 0 ձև, որտեղ D-ը ընդհանուր տատանումների խորհրդանիշն է (ի տարբերություն Համիլթոն-Օստրոգրադսկու սկզբունքի, այստեղ ոչ միայն կոորդինատներն ու արագությունները փոխվում են, այլև շարժման ժամանակը. համակարգը մեկ կոնֆիգուրացիայից մյուսը): N.d.p.v. Տվյալ դեպքում այն ​​գործում է միայն պահպանողական և առավել եւս հոլոնոմիկ համակարգերի համար, մինչդեռ առաջին դեպքում ոչ պահպանողական սկզբունքն ավելի ընդհանրական է և, մասնավորապես, կարող է տարածվել ոչ պահպանողական համակարգերի վրա։ Մեխանիկական շարժման հավասարումներ կազմելու համար օգտագործվում են N.D.P. համակարգերը և ուսումնասիրել այդ շարժումների ընդհանուր հատկությունները: Հասկացությունների համապատասխան ընդհանրացմամբ NDP-ն կիրառություն է գտնում շարունակական միջավայրի մեխանիկայում, էլեկտրադինամիկայի և քվանտում: մեխանիկա և այլն։

  • - նույնը, ինչ...

    Ֆիզիկական հանրագիտարան

  • - m-օպերատոր, մինիմալացման օպերատոր, - այլ ֆունկցիաներից նոր ֆունկցիաներ կառուցելու մեթոդ՝ բաղկացած հետևյալից...

    Մաթեմատիկական հանրագիտարան

  • - մեխանիկայի փոփոխական սկզբունքներից մեկը, ըստ որի՝ միմյանց հետ համեմատվող մեխանիկական շարժումների տվյալ դասի համար։ համակարգն իրականացվում է այն, ինչի համար գործողությունը նվազագույն է...

    Բնական գիտություն. Հանրագիտարանային բառարան

  • - մեխանիկայի ամենակարևոր օրենքներից մեկը, որը սահմանել է ռուս գիտնական Մ.Վ. Օստրոգրադսկի...

    Ռուսական հանրագիտարան

  • Իրավաբանական տերմինների բառարան

  • - մի շարք պետությունների սահմանադրական իրավունքում այն ​​սկզբունքը, ըստ որի միջազգային իրավունքի ընդհանուր ճանաչված սկզբունքներն ու նորմերը համապատասխան երկրի իրավական համակարգի անբաժանելի մասն են...

    Իրավաբանի հանրագիտարան

  • - մի շարք պետությունների սահմանադրական իրավունքում այն ​​սկզբունքը, ըստ որի միջազգային իրավունքի ընդհանուր ճանաչված նորմերը ազգային իրավական համակարգի անբաժանելի մասն են...

    Մեծ իրավական բառարան

  • - պայթուցիկ լիցքի կենտրոնից մինչև ազատ մակերես ամենակարճ հեռավորությունը - գիծ nai-malkoto դիմադրության վրա - křivka nejmenšího odporu - Line der geringsten Festigkeit - robbantás minimális ellenállási tengelyvonalala - hamgiin baga...

    Շինարարական բառարան

  • - եթե հնարավոր է դեֆորմացվող մարմնի կետերը տեղափոխել տարբեր ուղղություններով, ապա այս մարմնի յուրաքանչյուր կետ շարժվում է նվազագույն դիմադրության ուղղությամբ...

    Մետալուրգիայի հանրագիտարանային բառարան

  • - կանոն, որով առկա պաշարները սովորաբար գնահատվում են կա՛մ ամենացածր ինքնարժեքով, կա՛մ ամենացածր վաճառքի գնով...

    Բիզնեսի տերմինների բառարան

  • - մի շարք պետությունների սահմանադրական իրավունքում - այն սկզբունքը, ըստ որի միջազգային իրավունքի ընդհանուր ճանաչված սկզբունքներն ու նորմերը հանդիսանում են համապատասխան պետության իրավական համակարգի անբաժանելի մասը և գործում են...

    Տնտեսագիտության և իրավունքի հանրագիտարանային բառարան

  • - մեխանիկայի փոփոխական սկզբունքներից մեկը, ըստ որի՝ մեխանիկական համակարգի շարժումների տվյալ դասի համար միմյանց հետ համեմատած, վավեր է այն, որի համար ֆիզիկական մեծությունը,...
  • - նույնը, ինչ Գաուսի սկզբունքը...

    Խորհրդային մեծ հանրագիտարան

  • - մեխանիկայի փոփոխական սկզբունքներից մեկը. նույնը, ինչ նվազագույն գործողության սկզբունքը...

    Խորհրդային մեծ հանրագիտարան

  • - մեխանիկայի փոփոխական սկզբունքներից մեկը, ըստ որի մեխանիկական համակարգի շարժումների տվյալ դասի համար միմյանց հետ համեմատած, այն, որի համար գործողությունը նվազագույն է...

    Հանրագիտարանային մեծ բառարան

  • - Գիրք Ընտրեք գործողության ամենահեշտ մեթոդը՝ խուսափելով խոչընդոտներից, խուսափելով դժվարություններից...

    Ռուս գրական լեզվի դարձվածքաբանական բառարան

«ՆՈՔԻՆ ԱՐԺԵՔԻ ՍԿԶԲՈՒՆՔԸ» գրքերում

2.5.1. Սարքի շահագործման սկզբունքը

Entertaining Electronics [Օգտակար սխեմաների ոչ սովորական հանրագիտարան] գրքից հեղինակ Կաշկարով Անդրեյ Պետրովիչ

2.5.1. Սարքի շահագործման սկզբունքը Սարքի շահագործման սկզբունքը պարզ է. Երբ HL1 LED-ի արձակած լուսային հոսքը արտացոլվում է օբյեկտից և հարվածում է ֆոտոդետեկտորին, էլեկտրոնային միավորը, որն իրականացվում է 2 միկրոսխեմաների վրա՝ KR1401SA1 համեմատիչի և KR1006VI1 ժմչփի վրա, արտադրում է.

Թերաֆիմի գործողության սկզբունքը

Գաղտնի գիտելիք գրքից. Ագնի Յոգայի տեսություն և պրակտիկա հեղինակ Ռերիխ Ելենա Իվանովնա

Teraphim 02.24.39-ի գործարկման սկզբունքը Դուք գիտեք, որ ցանկացած օբյեկտի յուրաքանչյուր իրազեկում և ներկայացում դրանով մեզ ավելի է մոտեցնում դրան: Ինչպես գիտեք, առարկայի հոգեկան շերտերը կարող են տեղափոխվել նրա տերաֆիմ: հեռավոր աշխարհների աստղային տերաֆիմը և

Նվազագույն ջանքերի մասին օրենքի կիրառման երեք պայման

Դիպակ Չոպրայի իմաստությունը գրքից [Ստացեք այն, ինչ ցանկանում եք՝ հետևելով Տիեզերքի 7 օրենքներին] Թիմ Գուդմանի կողմից

Նվազագույն ջանքերի օրենքը գործելու երեք պայման Տեսնենք, թե ինչ պայմաններ են պահանջվում Տիեզերքից էներգիայի այս ստեղծագործական հոսքը դեպի ձեր կյանք ներգրավելու համար՝ սիրո էներգիան և հետևաբար, որպեսզի նվազագույն ջանքերի օրենքը սկսի գործել ձեր կյանքում։ .

Գլուխ 19 Նվազագույն ԱԶԴԵՑՈՒԹՅԱՆ ՍԿԶԲՈՒՆՔ

Գրքից 6. Էլեկտրադինամիկա հեղինակ Ֆեյնման Ռիչարդ Ֆիլիպս

Գլուխ 19 Նվազագույն ԱԶԴԵՑՈՒԹՅԱՆ ՍԿԶԲՈՒՆՔԸ Դասախոսությունից հետո կատարված հավելումը Երբ ես դպրոց էի, մեր ֆիզիկայի ուսուցիչը՝ Բադեր անունով, մի անգամ ինձ կանչեց դասից հետո և ասաց. մի հետաքրքիր բան լսեք

5. Նվազագույն գործողության սկզբունքը

Հեղափոխություն ֆիզիկայում գրքից դե Բրոլի Լուիի կողմից

5. Նվազագույն գործողության սկզբունքը Պոտենցիալ ուժերի դաշտում նյութական կետի դինամիկայի հավասարումները կարելի է ձեռք բերել այն սկզբունքի հիման վրա, որն ընդհանուր տերմիններով կոչվում է Համիլթոնի սկզբունք կամ անշարժ գործողության սկզբունք։ Այս սկզբունքով բոլորից

Գործողության սկզբունքը

Փականագործի ուղեցույց կողպեքների գրքից Ֆիլիպս Բիլի կողմից

Գործողության սկզբունքը Մխոցը պտտելու ունակությունը կախված է պտուտակների դիրքից, որն իր հերթին որոշվում է ձգողականությամբ, զսպանակների գործողությամբ և բանալու ուժով (կամ հիմնական բանալին; հիմնական բանալիների մասին տեղեկությունների համար տե՛ս Գլուխ 9): . Բանալու բացակայության դեպքում ձգողականությունը և զսպանակները սեղմվում են ներս

Ստացիոնար գործողության սկզբունքը

Հեղինակի Մեծ Սովետական ​​Հանրագիտարան (ՍՏ) գրքից TSB

Նվազագույն գործողության սկզբունքը

TSB

Նվազագույն հարկադրանքի սկզբունքը

Հեղինակի «Սովետական ​​մեծ հանրագիտարան» (ՆԱ) գրքից TSB

2.5.1. Գործողության սկզբունքը

Ռելեային պաշտպանություն էլեկտրական բաշխիչ ցանցերում B90 գրքից հեղինակ Բուլիչև Ալեքսանդր Վիտալևիչ

2.5.1. Գործողության սկզբունքը երկկողմանի սնուցմամբ և օղակաձև ցանցերում էլեկտրական ցանցերում սովորական հոսանքի պաշտպանությունը չի կարող ընտրովի գործել: Օրինակ՝ երկու հոսանքի աղբյուր ունեցող էլեկտրական ցանցում (նկ. 2.15), որտեղ երկու կողմից տեղադրված են անջատիչներ և պաշտպանիչներ.

Գործողության սկզբունքը

Turbo Suslik գրքից. Ինչպես դադարեցնել ինքդ քեզ խաբելուց և սկսել ապրել հեղինակ Լեուշկին Դմիտրի

Գործողության «Ընթացի՛ր սա» սկզբունքը, ըստ էության, մի տեսակ «մակրո» է, որը մեկ արտահայտությամբ գործարկում է ենթագիտակցականում մի ամբողջ փունջ գործընթացներ, որոնց նպատակը ընտրված մտավոր նյութի մշակումն է։ Այս կարգավորիչը ինքնին ներառում է 7 տարբեր մոդուլներ, որոնցից մի քանիսը

Ինչպես սկսել հետևել նվազագույն ջանքերի օրենքին. երեք անհրաժեշտ գործողություն

Ջոզեֆ Մերֆիի, Դեյլ Քարնեգիի, Էքհարթ Տոլլեի, Դիփակ Չոպրաի, Բարբարա Շերի, Նիլ Ուոլշի A Guide to Growing Capital գրքից հեղինակ Stern Valentin

Ինչպես սկսել հետևել Նվազագույն ջանքերի օրենքին. երեք անհրաժեշտ գործողություն Որպեսզի նվազագույն ջանքերի օրենքը սկսի գործել, դուք պետք է ոչ միայն կատարեք վերը նշված երեք պայմանները, այլև կատարեք երեք գործողություն: Առաջին գործողություն. սկսեք ընդունել աշխարհն այնպիսին, ինչպիսին այն է: Ընդունել է

11. Ֆիզիկա և Այկիդո ամենաքիչ գործողության

հեղինակ Մինդել Առնոլդ

11. Ֆիզիկա և Այկիդո ամենափոքր էֆեկտի Երբ փչում է, միայն քամի է։ Երբ անձրև է գալիս, միայն անձրև է գալիս: Երբ ամպերն անցնում են, արևը փայլում է նրանց միջով։ Եթե ​​դուք բացվում եք խորաթափանցության համար, ապա դուք մեկ եք խորաթափանցության հետ: Եվ դուք կարող եք ամբողջությամբ օգտագործել այն: Եթե ​​դու բացես

Լայբնիցի նվազագույն գործողության սկզբունքը «Vis Viva»

Երկրահոգեբանությունը շամանիզմում, ֆիզիկայում և դաոիզմում գրքից հեղինակ Մինդել Առնոլդ

Լայբնիցի նվազագույն գործողության սկզբունքը «Vis Viva» Նվազագույն գործողության սկզբունքի համար մենք բոլորս պետք է շնորհակալություն հայտնենք Վիլհելմ Գոտֆրիդ Լայբնիցին (1646–1716): Առաջին «ժամանակակից» ֆիզիկոսներից և մաթեմատիկոսներից մեկը՝ Լայբնիցն ապրել է Նյուտոնի ժամանակներում՝ մի դարաշրջան, երբ գիտնականներն ավելի բացահայտ էին.

Այկիդո - նվազագույն գործողության սկզբունքի մարմնացում

Երկրահոգեբանությունը շամանիզմում, ֆիզիկայում և դաոիզմում գրքից հեղինակ Մինդել Առնոլդ

Այկիդո՝ նվազագույն գործողության սկզբունքի մարմնացում Մեր հոգեբանությունն ու տեխնոլոգիան հիմնականում առաջնորդվում են նվազագույն գործողության գաղափարին շատ մոտ գաղափարով: Մենք անընդհատ փորձում ենք հեշտացնել մեր կյանքը։ Այսօրվա համակարգիչները բավականաչափ արագ չեն. Նրանք ստիպված են