Pada bagian ini kita akan membahas lebih lanjut tentang bentuk trigonometri bilangan kompleks. Bentuk demonstratif lebih jarang digunakan dalam tugas-tugas praktis. Saya sarankan mengunduh dan mencetak jika memungkinkan. tabel trigonometri, materi metodologis dapat ditemukan di halaman Rumus dan tabel matematika. Anda tidak bisa pergi jauh tanpa meja.
Bilangan kompleks apa pun (kecuali nol) dapat ditulis dalam bentuk trigonometri:
Dimana itu modulus bilangan kompleks, A - argumen bilangan kompleks.
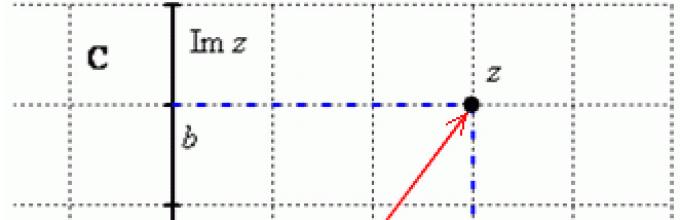
Mari kita nyatakan bilangan pada bidang kompleks. Untuk lebih jelas dan mudahnya penjelasannya, kami akan menempatkannya pada kuadran koordinat pertama, yaitu. kami percaya itu:

Modulus bilangan kompleks adalah jarak dari titik asal ke titik yang bersesuaian pada bidang kompleks. Sederhananya, modul adalah panjangnya vektor radius, yang ditunjukkan dengan warna merah pada gambar.
Modulus bilangan kompleks biasanya dilambangkan dengan: atau
Dengan menggunakan teorema Pythagoras, mudah untuk menurunkan rumus untuk mencari modulus bilangan kompleks: . Rumus ini benar untuk apa pun artinya "a" dan "menjadi".
Catatan : Modulus bilangan kompleks merupakan generalisasi konsep modulus bilangan real, sebagai jarak dari suatu titik ke titik asal.
Argumen bilangan kompleks ditelepon sudut di antara semi-sumbu positif sumbu nyata dan vektor jari-jari yang ditarik dari titik asal ke titik yang bersesuaian. Argumennya tidak didefinisikan untuk tunggal :.
Prinsip yang dibahas sebenarnya mirip dengan koordinat kutub, di mana jari-jari kutub dan sudut kutub menentukan suatu titik secara unik.
Argumen bilangan kompleks secara standar dilambangkan: atau
Dari pertimbangan geometris, kita memperoleh rumus berikut untuk mencari argumen:
. Perhatian! Rumus ini hanya bekerja pada setengah bidang kanan! Jika bilangan kompleks tidak terletak pada kuadran koordinat 1 atau 4, maka rumusnya akan sedikit berbeda. Kami juga akan menganalisis kasus-kasus ini.
Tapi pertama-tama, mari kita lihat contoh paling sederhana, kapan bilangan kompleks terletak pada sumbu koordinat.
Contoh 7
Mewakili bilangan kompleks dalam bentuk trigonometri: ,,,. Mari kita membuat gambarnya:

Faktanya, tugas tersebut bersifat lisan. Untuk lebih jelasnya, saya akan menulis ulang bentuk trigonometri bilangan kompleks:
Mari kita ingat dengan tegas, modul – panjang(yang selalu non-negatif), argumen – sudut
1) Mari kita nyatakan bilangan dalam bentuk trigonometri. Mari kita cari modulus dan argumennya. Jelas sekali. Perhitungan formal menggunakan rumus :. Jelas sekali (bilangan tersebut terletak tepat pada sumbu semi positif nyata). Jadi, bilangan dalam bentuk trigonometri :.
Tindakan pemeriksaan terbalik sangat jelas:
2) Mari kita nyatakan suatu bilangan dalam bentuk trigonometri. Mari kita cari modulus dan argumennya. Jelas sekali. Perhitungan formal menggunakan rumus :. Jelas (atau 90 derajat). Pada gambar, sudut ditandai dengan warna merah. Jadi bilangan dalam bentuk trigonometri adalah: ![]() .
.
Menggunakan , mudah untuk mendapatkan kembali bentuk aljabar dari bilangan tersebut (pada saat yang sama melakukan pemeriksaan):
3) Mari kita nyatakan suatu bilangan dalam bentuk trigonometri. Mari kita temukan modulnya dan
argumen. Sudah jelas bahwa. Perhitungan formal menggunakan rumus:
Jelas (atau 180 derajat). Pada gambar, sudutnya ditandai dengan warna biru. Jadi, bilangan dalam bentuk trigonometri :.
Penyelidikan:
4) Dan kasus menarik keempat. Jelas sekali. Perhitungan formal menggunakan rumus :.
Argumennya dapat ditulis dengan dua cara: Cara pertama: (270 derajat), dan karenanya: ![]() . Penyelidikan:
. Penyelidikan:
Namun, aturan berikut ini lebih standar: Jika sudutnya lebih besar dari 180 derajat, kemudian ditulis dengan tanda minus dan orientasi sudutnya berlawanan (“scrolling”): (minus 90 derajat), pada gambar sudutnya ditandai dengan warna hijau. Sangat mudah untuk menyadarinya
yang sudutnya sama.
Jadi, entri tersebut berbentuk: ![]()
Perhatian! Dalam hal apa pun Anda tidak boleh menggunakan paritas kosinus, keanehan sinus, dan selanjutnya “menyederhanakan” notasinya:
Ngomong-ngomong, ada gunanya mengingatnya penampilan dan sifat-sifat trigonometri dan invers fungsi trigonometri, bahan referensi terletak di paragraf terakhir halaman Grafik dan sifat-sifat fungsi dasar dasar. Dan bilangan kompleks akan dipelajari lebih mudah!
Dalam perancangan contoh paling sederhana, beginilah cara penulisannya: : "jelas modulusnya... jelas argumennya adalah...". Ini sangat jelas dan mudah diselesaikan secara lisan.
Mari kita beralih ke kasus-kasus yang lebih umum. Tidak ada masalah dengan modul ini, Anda harus selalu menggunakan rumusnya. Namun rumus mencari argumennya akan berbeda-beda, tergantung pada koordinat berapa bilangan tersebut berada. Dalam hal ini, tiga opsi dimungkinkan (berguna untuk menulis ulang):
1) Jika (koordinat kuarter ke-1 dan ke-4, atau setengah bidang kanan), maka argumennya harus dicari dengan menggunakan rumus.
2) Jika (koordinat kuarter ke-2), maka argumennya harus dicari dengan menggunakan rumus ![]() .
.
3) Jika (koordinat kuarter ke-3), maka argumennya harus dicari dengan menggunakan rumus ![]() .
.
Contoh 8
Mewakili bilangan kompleks dalam bentuk trigonometri: ,,,.
Karena sudah ada rumus yang sudah jadi, gambarnya tidak perlu diselesaikan. Namun ada satu hal: ketika Anda diminta untuk menyatakan suatu bilangan dalam bentuk trigonometri, maka Lebih baik tetap menggambar. Faktanya adalah solusi tanpa gambar seringkali ditolak oleh guru, tidak adanya gambar menjadi alasan serius terjadinya minus dan kegagalan.

Kami menyajikan angka-angka dalam bentuk kompleks, dan angka pertama dan ketiga akan digunakan untuk penyelesaian independen.
Mari kita nyatakan bilangan tersebut dalam bentuk trigonometri. Mari kita cari modulus dan argumennya.
Sejak (kasus 2), maka
– di sinilah Anda perlu memanfaatkan keanehan garis singgung busur. Sayangnya, tabel tersebut tidak memuat nilai , sehingga dalam kasus seperti ini argumennya harus dibiarkan dalam bentuk yang rumit: – bilangan dalam bentuk trigonometri.
Mari kita nyatakan bilangan tersebut dalam bentuk trigonometri. Mari kita cari modulus dan argumennya.
Sejak (kasus 1), maka (minus 60 derajat).
Dengan demikian:
![]() – bilangan dalam bentuk trigonometri.
– bilangan dalam bentuk trigonometri.
Tapi di sini, sebagaimana telah disebutkan, ada kekurangannya jangan sentuh.
Selain metode verifikasi grafis yang menyenangkan, ada juga verifikasi analitik yang sudah dilakukan pada Contoh 7. Kami menggunakan tabel nilai fungsi trigonometri, dengan tetap memperhatikan bahwa sudutnya persis dengan sudut meja (atau 300 derajat): – bilangan dalam bentuk aljabar aslinya.
Sajikan sendiri angka-angka dalam bentuk trigonometri. Solusi singkat dan jawaban di akhir pelajaran.
Di akhir bagian, secara singkat tentang bentuk eksponensial bilangan kompleks.
Bilangan kompleks apa pun (kecuali nol) dapat ditulis dalam bentuk eksponensial:
Dimana adalah modulus suatu bilangan kompleks, dan merupakan argumen dari bilangan kompleks tersebut.
Apa yang perlu Anda lakukan untuk merepresentasikan bilangan kompleks dalam bentuk eksponensial? Hampir sama: jalankan gambar, temukan modul dan argumen. Dan tulis nomornya di formulir.
Misalnya untuk bilangan pada contoh sebelumnya kita telah menemukan modul dan argumen :,. Kemudian nomor yang diberikan dalam bentuk eksponensial akan ditulis sebagai berikut :.
Angka dalam bentuk eksponensial akan terlihat seperti ini:
Nomor ![]() - Jadi:
- Jadi:
Satu-satunya saran adalah jangan sentuh indikatornya eksponen, tidak perlu menata ulang faktor, membuka tanda kurung, dll. Bilangan kompleks ditulis dalam bentuk eksponensial dengan ketat menurut bentuk.
3.1. Koordinat kutub
Sering digunakan di pesawat sistem koordinat kutub . Didefinisikan jika suatu titik O diberikan, disebut tiang, dan sinar yang memancar dari kutub (bagi kami ini adalah porosnya Sapi) – sumbu kutub. Posisi titik M ditentukan oleh dua angka: radius (atau vektor radius) dan sudut φ antara sumbu kutub dan vektor. Sudut φ disebut sudut kutub; diukur dalam radian dan dihitung berlawanan arah jarum jam dari sumbu kutub.
Posisi suatu titik dalam sistem koordinat kutub ditentukan oleh pasangan bilangan terurut (r; φ). Di Kutub r = 0, dan φ tidak terdefinisi. Untuk semua poin lainnya r > 0, dan φ didefinisikan hingga suku yang merupakan kelipatan 2π. Dalam hal ini, pasangan bilangan (r; φ) dan (r 1 ; φ 1) diasosiasikan pada titik yang sama jika .
Untuk sistem koordinat persegi panjang xOy Koordinat kartesius suatu titik dapat dengan mudah dinyatakan dalam koordinat kutubnya sebagai berikut:
3.2. Interpretasi geometris bilangan kompleks
 Pertimbangkan sistem koordinat persegi panjang Cartesian pada bidang xOy.
Pertimbangkan sistem koordinat persegi panjang Cartesian pada bidang xOy.
Bilangan kompleks apa pun z=(a, b) dikaitkan dengan suatu titik pada bidang dengan koordinat ( x, kamu), Di mana koordinat x = a, yaitu bagian real bilangan kompleks, dan koordinat y = bi adalah bagian imajinernya.
Bidang yang titik-titiknya merupakan bilangan kompleks adalah bidang kompleks.
Pada gambar tersebut, bilangan kompleks z = (a,b) sesuai dengan suatu titik M(x, kamu).
Latihan.Gambarlah bidang koordinat bilangan kompleks:
3.3. Bentuk trigonometri bilangan kompleks
Suatu bilangan kompleks pada bidang mempunyai koordinat suatu titik L(x;y). Di mana:
Menulis bilangan kompleks ![]() - bentuk trigonometri bilangan kompleks.
- bentuk trigonometri bilangan kompleks.
Nomor r dipanggil modul
bilangan kompleks z dan ditunjuk. Modulus adalah bilangan real non-negatif. Untuk ![]() .
.
Modulusnya nol jika dan hanya jika z = 0, yaitu a = b = 0.
Nomor φ disebut argumen z dan ditunjuk. Argumen z didefinisikan secara ambigu, seperti sudut kutub pada sistem koordinat kutub, yaitu sampai suku kelipatan 2π.
Lalu kita terima: , dimana φ adalah nilai argumen terkecil. Jelas sekali
![]() .
.
Saat mempelajari topik secara lebih mendalam, argumen tambahan φ* diperkenalkan, sehingga
Contoh 1. Temukan bentuk trigonometri bilangan kompleks.
Larutan. 1) pertimbangkan modul: ;
2) mencari φ: ![]() ;
;
3) bentuk trigonometri: ![]()
Contoh 2. Temukan bentuk aljabar dari bilangan kompleks ![]() .
.
Di sini cukup dengan mengganti nilai fungsi trigonometri dan mengubah ekspresi:
 Contoh 3. Temukan modulus dan argumen bilangan kompleks;
Contoh 3. Temukan modulus dan argumen bilangan kompleks;
1)  ;
;
2) ; φ – dalam 4 kuartal:
3.4. Operasi bilangan kompleks dalam bentuk trigonometri
· Penambahan dan pengurangan Lebih mudah melakukannya dengan bilangan kompleks dalam bentuk aljabar:
· Perkalian- dengan bantuan sederhana transformasi trigonometri hal itu dapat ditunjukkan bahwa Saat mengalikan, modul angka dikalikan, dan argumen ditambahkan: ;
Operasi bilangan kompleks ditulis dalam bentuk aljabar
Bentuk aljabar bilangan kompleks z =(A,B).disebut ekspresi aljabar dari bentuk
z = A + dua.
Operasi aritmatika pada bilangan kompleks z 1 = sebuah 1 +b 1 Saya Dan z 2 = sebuah 2 +b 2 Saya, ditulis dalam bentuk aljabar, dilakukan sebagai berikut.
1. Jumlah (selisih) bilangan kompleks
z 1 ±z 2 = (A 1 ± sebuah 2) + (B 1 ±b 2)∙saya,
itu. penjumlahan (pengurangan) dilakukan menurut aturan penjumlahan polinomial dengan pengurangan suku-suku sejenis.
2. Hasil kali bilangan kompleks
z 1 ∙z 2 = (A 1 ∙a 2 -B 1 ∙b 2) + (A 1 ∙b 2 +a 2 ∙b 1)∙saya,
itu. perkalian dilakukan menurut aturan biasa untuk mengalikan polinomial, dengan memperhatikan fakta itu Saya 2 = 1.
3. Pembagian dua bilangan kompleks dilakukan menurut aturan selanjutnya:
, (z 2 ≠ 0),
itu. pembagian dilakukan dengan mengalikan pembagi dan pembagi dengan bilangan konjugasi pembaginya.
Eksponen bilangan kompleks didefinisikan sebagai berikut:
Sangat mudah untuk menunjukkan hal itu

Contoh.
1. Temukan jumlah bilangan kompleks z 1 = 2 – Saya Dan z 2 = – 4 + 3Saya.
z 1 + z 2 = (2 + (–1)∙saya)+ (–4 + 3Saya) = (2 + (–4)) + ((–1) + 3) Saya = –2+2Saya.
2. Temukan produk bilangan kompleks z 1 = 2 – 3Saya Dan z 2 = –4 + 5Saya.
= (2 – 3Saya) ∙ (–4 + 5Saya) = 2 ∙(–4) + (-4) ∙(–3Saya)+ 2∙5Saya– 3saya∙ 5saya = 7+22Saya.
3. Temukan hasil bagi z dari divisi z 1 = 3 – 2na z 2 = 3 – Saya.
z = .
4. Selesaikan persamaan: , X Dan kamu Î R.
(2x+y) + (x+y)saya = 2 + 3Saya.
Karena persamaan bilangan kompleks kita mempunyai:
Di mana x =–1 , kamu= 4.
5. Hitung: Saya 2 ,Saya 3 ,Saya 4 ,Saya 5 ,Saya 6 ,Saya -1 ,Saya -2 .

6. Hitung jika .
![]() .
.
7. Hitung suatu angka kebalikan dari angka z=3-Saya.
Bilangan kompleks dalam bentuk trigonometri
Pesawat yang kompleks disebut bidang dengan koordinat kartesius ( x, kamu), jika setiap titik dengan koordinat ( a, b) dikaitkan dengan bilangan kompleks z = a + dua. Dalam hal ini disebut sumbu absis sumbu nyata, dan sumbu ordinatnya adalah imajiner. Lalu setiap bilangan kompleks a+bi digambarkan secara geometris pada bidang sebagai sebuah titik A (a,b) atau vektor.
Oleh karena itu, posisi intinya A(dan, oleh karena itu, bilangan kompleks z) dapat ditentukan dengan panjang vektor | | = R dan sudut J, dibentuk oleh vektor | | dengan arah positif sumbu nyata. Panjang vektor disebut modulus bilangan kompleks dan dilambangkan dengan | z |=r, dan sudutnya J ditelepon argumen bilangan kompleks dan ditunjuk j = arg z.
Jelas bahwa | z| ³ 0 dan | z | = 0 Û z = 0.
Dari Gambar. 2 jelas bahwa.
Argumen bilangan kompleks ditentukan secara ambigu, tetapi dengan akurasi 2 hal, kÎ Z.
Dari Gambar. 2 juga jelas bahwa jika z=a+bi Dan j=argumen z, Itu
karena j =, dosa j =, hal j = .
Jika zÎR Dan z> 0, lalu argumen z = 0 +2pk;
Jika z ОR Dan z< 0, lalu argumen z = p + 2pk;
Jika z = 0,argumen z tidak terbatas.
Nilai utama argumen ditentukan pada interval 0 £argumen z£2 P,
atau -P£ arg z £ hal.
Contoh:
1. Temukan modulus bilangan kompleks z 1 = 4 – 3Saya Dan z 2 = –2–2Saya.
2. Tentukan luas bidang kompleks yang ditentukan oleh kondisi:
1) | z | = 5; 2) | z| £6; 3) | z – (2+Saya) | £3; 4) £6 | z – Saya| £7.
Solusi dan jawaban:
1) | z| = 5 Û Û - persamaan lingkaran dengan jari-jari 5 dan berpusat di titik asal.
2) Lingkaran berjari-jari 6 dan berpusat di titik asal.
3) Lingkaran berjari-jari 3 dan berpusat di suatu titik z 0 = 2 + Saya.
4) Sebuah cincin yang dibatasi oleh lingkaran berjari-jari 6 dan 7 yang berpusat di suatu titik z 0 = Saya.
3. Tentukan modulus dan argumen bilangan: 1) ; 2) .
1) ; A = 1, B = Þ ![]() ,
,
 Þ j 1 =
Þ j 1 = ![]() .
.
2) z 2 = –2 – 2Saya; sebuah =–2, b =-2Þ ![]() ,
,
 .
.
Petunjuk: Saat menentukan argumen utama, gunakan bidang kompleks.
Dengan demikian: z 1 = .
2) ![]() , R 2 =
1, j 2 = ,
, R 2 =
1, j 2 = , ![]() .
.
3) ![]() , R 3 = 1, j 3 = ,
, R 3 = 1, j 3 = , ![]() .
.
4) , R 4 = 1, j 4 = , ![]() .
.
ANGKA KOMPLEKS XI
§ 256. Bentuk trigonometri bilangan kompleks
Biarkan bilangan kompleks a+bi vektor yang sesuai O.A.> dengan koordinat ( a, b ) (lihat Gambar 332).
Mari kita nyatakan panjang vektor ini dengan R , dan sudut yang dibuatnya dengan sumbu X , melalui φ . Menurut definisi sinus dan cosinus:
A / R = karena φ , B / R = dosa φ .
Itu sebabnya A = R karena φ , B = R dosa φ . Namun dalam kasus ini bilangan kompleks a+bi dapat ditulis sebagai:
a+bi = R karena φ + ir dosa φ = R (kos φ + Saya dosa φ ).
Seperti yang Anda ketahui, kuadrat panjang suatu vektor sama dengan jumlah kuadrat koordinatnya. Itu sebabnya R 2 = A 2 + B 2, dari mana R = √a 2 + B 2
Jadi, bilangan kompleks apa pun a+bi dapat direpresentasikan dalam bentuk :
a+bi = R (kos φ + Saya dosa φ ), (1)
dimana r = √a 2 + B 2 dan sudutnya φ ditentukan dari kondisi:

Bentuk penulisan bilangan kompleks disebut trigonometri.
Nomor R dalam rumus (1) disebut modul, dan sudutnya φ - argumen, bilangan kompleks a+bi .
Jika bilangan kompleks a+bi tidak sama dengan nol, maka modulusnya positif; jika a+bi = 0, maka a = b = 0 dan kemudian R = 0.
Modulus bilangan kompleks ditentukan secara unik.
Jika bilangan kompleks a+bi tidak sama dengan nol, maka argumennya ditentukan oleh rumus (2) tentu saja akurat hingga sudut habis dibagi 2 π . Jika a+bi = 0, maka a = b = 0. Dalam hal ini R = 0. Dari rumus (1) mudah dipahami sebagai argumen φ dalam hal ini, Anda dapat memilih sudut mana pun: lagipula, untuk sudut mana pun φ
0 (kos φ + Saya dosa φ ) = 0.
Oleh karena itu argumen nol tidak terdefinisi.
Modulus bilangan kompleks R terkadang dilambangkan | z |, dan argumen argumen z . Mari kita lihat beberapa contoh representasi bilangan kompleks dalam bentuk trigonometri.
Contoh. 1. 1 + Saya .
Mari kita temukan modulnya R dan argumen φ nomor ini.
R = √ 1 2 + 1 2 = √ 2 .
Oleh karena itu dosa φ = 1 / √ 2, cos φ = 1 / √ 2, dari mana φ = π / 4 + 2Nπ .
Dengan demikian,
1 + Saya = √ 2 ,
Di mana P - bilangan bulat apa pun. Biasanya, dari himpunan nilai argumen bilangan kompleks yang tak terhingga, dipilih satu nilai antara 0 dan 2 π . Dalam hal ini, nilai ini adalah π / 4. Itu sebabnya
1 + Saya = √ 2 (kos π / 4 + Saya dosa π / 4)
Contoh 2. Tuliskan bilangan kompleks dalam bentuk trigonometri √ 3 - Saya . Kita punya:
R = √ 3+1 = 2, cos φ = √ 3/2, dosa φ = - 1 / 2
Oleh karena itu, sampai suatu sudut habis dibagi 2 π , φ = 11 / 6 π ; karena itu,
√ 3 - Saya = 2(karena 11/6 π + Saya dosa 11/6 π ).
Contoh 3 Tuliskan bilangan kompleks dalam bentuk trigonometri Saya.

Bilangan kompleks Saya vektor yang sesuai O.A.> , berakhir di titik A sumbu pada dengan ordinat 1 (Gbr. 333). Panjang vektor tersebut adalah 1, dan sudut yang dibentuknya terhadap sumbu x adalah sama dengan π / 2. Itu sebabnya
Saya = karena π / 2 + Saya dosa π / 2 .
Contoh 4. Tuliskan bilangan kompleks 3 dalam bentuk trigonometri.
Bilangan kompleks 3 berhubungan dengan vektor O.A. > X absis 3 (Gbr. 334).

Panjang vektor tersebut adalah 3, dan sudut yang dibentuknya terhadap sumbu x adalah 0. Oleh karena itu
3 = 3 (karena 0 + Saya dosa 0),
Contoh 5. Tuliskan bilangan kompleks -5 dalam bentuk trigonometri.

Bilangan kompleks -5 berhubungan dengan vektor O.A.> berakhir pada suatu titik sumbu X dengan absis -5 (Gbr. 335). Panjang vektor tersebut adalah 5, dan sudut yang dibentuknya terhadap sumbu x adalah sama dengan π . Itu sebabnya
5 = 5(kos π + Saya dosa π ).
Latihan
2047. Tuliskan bilangan kompleks berikut dalam bentuk trigonometri, tentukan modul dan argumennya:
1) 2 + 2√3 Saya , 4) 12Saya - 5; 7).3Saya ;
2) √3 + Saya ; 5) 25; 8) -2Saya ;
3) 6 - 6Saya ; 6) - 4; 9) 3Saya - 4.
2048. Tunjukkan pada bidang sekumpulan titik yang mewakili bilangan kompleks yang moduli r dan argumennya memenuhi syarat:
1) R = 1, φ = π / 4 ; 4) R < 3; 7) 0 < φ < π / 6 ;
2) R =2; 5) 2 < R <3; 8) 0 < φ < я;
3) R < 3; 6) φ = π / 3 ; 9) 1 < R < 2,
10) 0 < φ < π / 2 .
2049. Bisakah bilangan sekaligus menjadi modulus bilangan kompleks? R Dan - R ?
2050. Bisakah argumen bilangan kompleks sekaligus berupa sudut? φ Dan - φ ?
Sajikan bilangan kompleks ini dalam bentuk trigonometri, dengan mendefinisikan modul dan argumennya:
2051*. 1 + karena α + Saya dosa α . 2054*. 2(karena 20° - Saya dosa 20°).
2052*. dosa φ + Saya karena φ . 2055*. 3(- karena 15° - Saya dosa 15°).