Temukan proyeksi vektor a pada sumbu koordinat. Operasi linier pada vektor. Teorema proyeksi vektor

Menyelesaikan masalah keseimbangan gaya-gaya konvergen dengan membuat poligon gaya tertutup memerlukan konstruksi yang rumit. Metode universal untuk menyelesaikan masalah seperti itu adalah dengan melanjutkan menentukan proyeksi gaya-gaya tertentu ke sumbu koordinat dan mengoperasikan proyeksi ini. Sumbu adalah garis lurus yang mempunyai arah tertentu.

Proyeksi suatu vektor ke suatu sumbu merupakan besaran skalar, yang ditentukan oleh ruas sumbu yang dipotong oleh garis tegak lurus yang dijatuhkan ke atasnya dari awal dan akhir vektor.

Suatu proyeksi vektor dianggap positif jika arah dari awal proyeksi sampai akhir bertepatan dengan arah positif sumbu. Suatu proyeksi vektor dianggap negatif jika arah dari awal proyeksi sampai akhir berlawanan dengan arah positif sumbu.

Jadi, proyeksi gaya pada sumbu koordinat sama dengan hasil kali modulus gaya dan kosinus sudut antara vektor gaya dan arah positif sumbu.

Mari kita perhatikan beberapa kasus memproyeksikan gaya ke suatu sumbu:

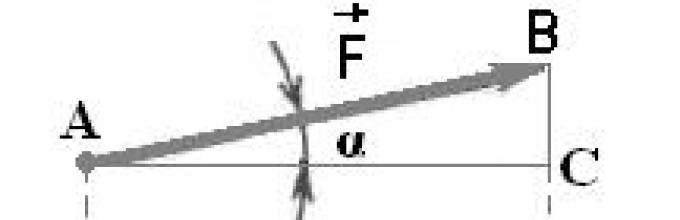
Vektor gaya F(Gbr. 15) membentuk sudut lancip dengan arah positif sumbu x.

Untuk mencari proyeksi, dari awal dan akhir vektor gaya kita turunkan garis tegak lurus terhadap sumbu Oh; kita mendapatkan

1. Fx = F karena α

Proyeksi vektor dalam hal ini adalah positif

Memaksa F(Gbr. 16) dengan arah sumbu positif X sudut tumpul α.

Kemudian F x = F cos α, tetapi karena α = 180 0 - φ,

F x = F karena α = F cos180 0 - φ =- F karena φ.

Proyeksi kekuatan F per sumbu Oh dalam hal ini negatif.

Memaksa F(Gbr. 17) tegak lurus terhadap sumbu Oh.

Proyeksi gaya F pada sumbu X sama dengan nol

F x = F karena 90° = 0.

Kekuatan terletak di pesawat bagaimana(Gbr. 18), dapat diproyeksikan pada dua sumbu koordinat Oh Dan kamu.

Kekuatan F dapat dipecah menjadi beberapa komponen: F x dan F kamu. Modul vektor F x sama dengan proyeksi vektor F per sumbu sapi, dan modulus vektor F y sama dengan proyeksi vektor F per sumbu Oh.

Dari Δ OAV: F x = F karena α, F x = F dosa α.

Dari Δ OAS: F x = F karena φ, F x = F dosa φ.

Besarnya gaya dapat dicari dengan menggunakan teorema Pythagoras:

Proyeksi suatu penjumlahan atau resultan vektor pada suatu sumbu sama dengan jumlah aljabar proyeksi penjumlahan vektor-vektor tersebut pada sumbu yang sama.

Pertimbangkan kekuatan-kekuatan yang berkumpul F 1 , F 2 , F 3, dan F 4, (Gbr. 19, a). Jumlah geometris, atau resultan, gaya-gaya ini F ditentukan oleh sisi penutup poligon gaya

Mari kita turunkan dari titik sudut poligon gaya ke sumbunya X tegak lurus.

Mempertimbangkan proyeksi gaya yang diperoleh langsung dari konstruksi yang telah selesai, kita punya

F= F 1x+ F 2x+ F 3x+ F 4x

dimana n adalah banyaknya suku vektor. Proyeksinya masuk ke persamaan di atas dengan tanda yang sesuai.

Dalam sebuah bidang, jumlah gaya geometris dapat diproyeksikan ke dua sumbu koordinat, dan di ruang angkasa, masing-masing, ke tiga sumbu.

Pertama, mari kita ingat apa itu sumbu koordinat, proyeksi suatu titik ke suatu sumbu Dan koordinat suatu titik pada sumbu.

Sumbu koordinat- Ini adalah garis lurus yang diberi arah tertentu. Anda dapat menganggapnya sebagai vektor dengan modulus yang sangat besar.

Sumbu koordinat dilambangkan dengan beberapa huruf: X, Y, Z, s, t... Biasanya suatu titik dipilih (sewenang-wenang) pada sumbu, yang disebut titik asal dan, biasanya, dilambangkan dengan huruf O. Dari titik ini jarak ke tempat menarik lainnya bagi kami diukur.

Proyeksi suatu titik ke suatu sumbu- ini adalah alas garis tegak lurus yang diturunkan dari titik ini ke sumbu ini (Gbr. 8). Artinya, proyeksi suatu titik pada sumbunya adalah sebuah titik.

Koordinat titik pada sumbu- ini adalah bilangan yang nilai absolutnya sama dengan panjang segmen sumbu (pada skala yang dipilih) yang terdapat di antara titik asal sumbu dan proyeksi titik ke sumbu tersebut. Angka ini diambil dengan tanda plus jika proyeksi titik tersebut terletak pada arah sumbu dari titik asal dan dengan tanda minus jika berlawanan arah.

Proyeksi skalar suatu vektor ke suatu sumbu- Ini nomor, yang nilai absolutnya sama dengan panjang segmen sumbu (pada skala yang dipilih) yang berada di antara proyeksi titik awal dan titik akhir vektor. Penting! Biasanya bukan ekspresi proyeksi skalar suatu vektor ke suatu sumbu mereka hanya mengatakan - proyeksi vektor ke sumbu, yaitu kata skalar diturunkan. Proyeksi vektor dilambangkan dengan huruf yang sama dengan vektor yang diproyeksikan (dalam tulisan normal, tidak tebal), dengan indeks yang lebih rendah (sebagai aturan) dari nama sumbu di mana vektor ini diproyeksikan. Misalnya, jika sebuah vektor diproyeksikan ke sumbu X A, maka proyeksinya dilambangkan dengan a x. Saat memproyeksikan vektor yang sama ke sumbu lain, katakanlah sumbu Y, proyeksinya akan dilambangkan dengan y (Gbr. 9).

Menghitung proyeksi vektor ke sumbu(misalnya sumbu X), maka perlu dikurangi koordinat titik awal dari koordinat titik akhirnya, yaitu

ax = xk − xn.

Kita harus ingat: proyeksi skalar suatu vektor ke suatu sumbu (atau, sederhananya, proyeksi suatu vektor ke suatu sumbu) adalah suatu bilangan (bukan vektor)! Apalagi proyeksinya bisa positif jika nilai xk lebih besar dari nilai xn, negatif jika nilai xk lebih kecil dari nilai xn dan sama dengan nol jika xk sama dengan xn (Gbr. 10).

Proyeksi suatu vektor pada suatu sumbu juga dapat diketahui dengan mengetahui modulus vektor dan sudut yang dibuatnya terhadap sumbu tersebut.

Dari Gambar 11 terlihat jelas bahwa a x = a Cos α

Artinya, proyeksi vektor ke sumbu sama dengan produk modulus vektor dan kosinus sudut antara arah sumbu dan arah vektor. Jika sudutnya lancip, maka Cos α > 0 dan a x > 0, dan jika tumpul, maka kosinus sudut tumpul tersebut negatif, dan proyeksi vektor pada sumbunya juga negatif.

Sudut yang diukur dari sumbu berlawanan arah jarum jam dianggap positif, dan sudut yang diukur sepanjang sumbu dianggap negatif. Namun, karena kosinus merupakan fungsi genap, yaitu Cos α = Cos (− α), saat menghitung proyeksi, sudut dapat dihitung searah jarum jam dan berlawanan arah jarum jam.

Saat menyelesaikan masalah, sifat proyeksi berikut akan sering digunakan: jika

A = B + C +…+ D, maka a x = b x + c x +…+ d x (mirip dengan sumbu lainnya),

A= m B, maka a x = mb x (demikian pula untuk sumbu lainnya).

Rumusnya a x = a Cos α akan menjadi Sering terjadi ketika menyelesaikan masalah, jadi kamu pasti perlu mengetahuinya. Anda perlu mengetahui aturan untuk menentukan proyeksi dengan hati!

Ingat!

Untuk mencari proyeksi suatu vektor pada suatu sumbu, modulus vektor tersebut harus dikalikan dengan kosinus sudut antara arah sumbu dan arah vektor.

Sekali lagi - dengan hati!

Proyeksi vektor pada suatu sumbu adalah vektor yang diperoleh dengan mengalikan proyeksi skalar suatu vektor pada sumbu tersebut dan vektor satuan pada sumbu tersebut. Misalnya, jika x – proyeksi skalar vektor A ke sumbu X, lalu a x Saya- proyeksi vektornya ke sumbu ini.

Mari kita tunjukkan proyeksi vektor sama dengan vektor itu sendiri, tetapi dengan indeks sumbu di mana vektor tersebut diproyeksikan. Jadi, proyeksi vektor dari vektor A pada sumbu X kami menyatakannya A X( gemuk huruf yang menunjukkan vektor dan subskrip dari nama sumbu) atau (huruf tidak tebal yang menunjukkan vektor, tetapi dengan panah di bagian atas (!) dan subskrip dari nama sumbu).

Proyeksi skalar vektor per sumbu disebut nomor, yang nilai absolutnya sama dengan panjang segmen sumbu (pada skala yang dipilih) yang berada di antara proyeksi titik awal dan titik akhir vektor. Biasanya bukan ekspresi proyeksi skalar mereka hanya mengatakan - proyeksi. Proyeksi dilambangkan dengan huruf yang sama dengan vektor yang diproyeksikan (dalam penulisan normal, tidak tebal), dengan indeks yang lebih rendah (sebagai aturan) dari nama sumbu di mana vektor ini diproyeksikan. Misalnya, jika sebuah vektor diproyeksikan ke sumbu X A, maka proyeksinya dilambangkan dengan a x. Ketika memproyeksikan vektor yang sama ke sumbu lain, jika sumbunya adalah Y, proyeksinya akan dilambangkan dengan y.

Untuk menghitung proyeksi vektor pada suatu sumbu (misalnya sumbu X), koordinat titik awal perlu dikurangi dari koordinat titik akhirnya, yaitu
ax = xk − xn.
Proyeksi suatu vektor pada suatu sumbu adalah suatu bilangan. Apalagi proyeksinya bisa positif jika nilai x k lebih besar dari nilai x n,

negatif jika nilai x k lebih kecil dari nilai x n

dan sama dengan nol jika x k sama dengan x n.

Proyeksi suatu vektor pada suatu sumbu juga dapat diketahui dengan mengetahui modulus vektor dan sudut yang dibuatnya terhadap sumbu tersebut.

Dari gambar tersebut terlihat jelas bahwa a x = a Cos α

yaitu proyeksi vektor ke sumbu sama dengan hasil kali modulus vektor dan kosinus sudut antara arah sumbu dan arah vektor. Jika sudutnya lancip, maka
Cos α > 0 dan a x > 0, dan jika tumpul, maka kosinus sudut tumpul tersebut negatif, dan proyeksi vektor ke sumbu juga akan negatif.

Sudut yang diukur dari sumbu berlawanan arah jarum jam dianggap positif, dan sudut yang diukur sepanjang sumbu dianggap negatif. Namun, karena kosinus merupakan fungsi genap, yaitu Cos α = Cos (− α), saat menghitung proyeksi, sudut dapat dihitung searah jarum jam dan berlawanan arah jarum jam.

Untuk mencari proyeksi suatu vektor pada suatu sumbu, modulus vektor tersebut harus dikalikan dengan kosinus sudut antara arah sumbu dan arah vektor.

Koordinat vektor— koefisien dari satu-satunya kombinasi linier yang mungkin dari vektor-vektor basis dalam sistem koordinat yang dipilih, sama dengan vektor yang diberikan.

di mana koordinat vektornya.

Produk titik dari vektor

Produk skalar vektor[- dalam dimensi terbatas ruang vektor didefinisikan sebagai jumlah produk dari komponen identik yang dikalikan vektor.

Misalnya, S.p.v. A = (A 1 , ..., sebuah) Dan B = (B 1 , ..., bn):

(A , B ) = A 1 B 1 + A 2 B 2 + ... + a n b n

Dalam fisika untuk kelas 9 (I.K.Kikoin, A.K.Kikoin, 1999),
tugas №5
ke bab " BAB 1. INFORMASI UMUM TENTANG LALU LINTAS».

1. Apa yang disebut proyeksi suatu vektor pada sumbu koordinat?

1. Proyeksi vektor a pada sumbu koordinat adalah panjang ruas antara proyeksi awal dan akhir vektor a (tegak lurus yang dijatuhkan dari titik-titik tersebut ke sumbu) pada sumbu koordinat tersebut.

2. Bagaimana hubungan vektor perpindahan suatu benda dengan koordinatnya?

2. Proyeksi vektor perpindahan s pada sumbu koordinat sama dengan perubahan koordinat benda yang bersangkutan.

3. Jika koordinat suatu titik bertambah seiring waktu, maka tanda apa yang dimiliki proyeksi vektor perpindahan pada sumbu koordinat? Bagaimana jika berkurang?

3. Jika koordinat suatu titik bertambah seiring waktu, maka proyeksi vektor perpindahan ke sumbu koordinat akan bernilai positif, karena dalam hal ini kita akan beralih dari proyeksi awal ke proyeksi akhir vektor searah sumbu itu sendiri.

Jika koordinat suatu titik semakin mengecil, maka proyeksi vektor perpindahan terhadap sumbu koordinat akan bernilai negatif, karena dalam hal ini kita akan beralih dari proyeksi awal ke proyeksi akhir vektor terhadap pemandu sumbu itu sendiri.

4. Jika vektor perpindahan sejajar dengan sumbu X, berapakah modulus proyeksi vektor pada sumbu tersebut? Lalu bagaimana dengan modulus proyeksi vektor yang sama pada sumbu Y?

4. Jika vektor perpindahan sejajar dengan sumbu X, maka modulus proyeksi vektor ke sumbu tersebut sama dengan modulus vektor itu sendiri, dan proyeksinya ke sumbu Y adalah nol.

5. Tentukan tanda-tanda proyeksi pada sumbu X dari vektor-vektor perpindahan yang ditunjukkan pada Gambar 22. Bagaimana koordinat benda berubah selama perpindahan tersebut?

5. Dalam semua kasus berikut, koordinat Y benda tidak berubah, dan koordinat X benda akan berubah sebagai berikut:

a) hal 1;

proyeksi vektor s 1 ke sumbu X adalah negatif dan nilai absolutnya sama dengan panjang vektor s 1 . Dengan gerakan seperti itu, koordinat X benda akan berkurang sebesar panjang vektor s 1.

b) hal 2 ;

proyeksi vektor s 2 pada sumbu X adalah positif dan besarnya sama dengan panjang vektor s 1 . Dengan gerakan seperti itu, koordinat X benda akan bertambah panjang vektor s 2.

c) hal 3 ;

proyeksi vektor s 3 ke sumbu X adalah negatif dan besarnya sama dengan panjang vektor s 3 . Dengan gerakan seperti itu, koordinat X benda akan berkurang sebesar panjang vektor s 3.

d)s 4;

proyeksi vektor s 4 pada sumbu X adalah positif dan besarnya sama dengan panjang vektor s 4 . Dengan gerakan seperti itu, koordinat X benda akan bertambah panjang vektor s 4.

e) hal 5;

proyeksi vektor s 5 pada sumbu X bernilai negatif dan besarnya sama dengan panjang vektor s 5 . Dengan gerakan seperti itu, koordinat X benda akan berkurang sebesar panjang vektor s 5.

6. Jika nilai jarak yang ditempuh besar, apakah modul perpindahannya bisa kecil?

6. Mungkin. Hal ini disebabkan perpindahan (vektor perpindahan) merupakan besaran vektor, yaitu adalah ruas garis lurus berarah yang menghubungkan posisi awal benda dengan posisi selanjutnya. Dan posisi akhir benda (berapapun jarak yang ditempuh) dapat sedekat yang diinginkan dengan posisi awal benda. Jika posisi akhir dan awal benda bertepatan, modulus perpindahan akan sama dengan nol.

7. Mengapa vektor gerak suatu benda dalam mekanika lebih penting daripada lintasan yang ditempuhnya?

7. Tugas utama mekanika adalah menentukan posisi benda pada suatu waktu. Mengetahui vektor gerak suatu benda, kita dapat menentukan koordinat benda tersebut, yaitu. posisi benda pada suatu saat, dan hanya mengetahui jarak yang ditempuh, kita tidak dapat menentukan koordinat benda, karena kita tidak memiliki informasi tentang arah pergerakan, tetapi hanya dapat menilai panjang jalur yang ditempuh pada waktu tertentu.

Sumbu adalah arahnya. Artinya proyeksi pada suatu sumbu atau pada garis berarah dianggap sama. Proyeksi dapat berbentuk aljabar atau geometris. Dalam istilah geometri, proyeksi suatu vektor pada suatu sumbu dipahami sebagai vektor, dan dalam istilah aljabar dipahami sebagai bilangan. Artinya, konsep proyeksi vektor ke suatu sumbu dan proyeksi numerik suatu vektor ke suatu sumbu digunakan.

Jika kita mempunyai sumbu L dan vektor bukan nol A B →, maka kita dapat membuat vektor A 1 B 1 ⇀, yang menyatakan proyeksi titik-titiknya A 1 dan B 1.

A 1 B → 1 akan menjadi proyeksi vektor A B → ke L.

Definisi 1

Proyeksi vektor ke sumbu adalah vektor yang awal dan akhirnya merupakan proyeksi awal dan akhir suatu vektor tertentu. n p L A B → → biasanya dilambangkan dengan proyeksi A B → ke L. Untuk membuat proyeksi ke L, garis tegak lurus dijatuhkan ke L.

Contoh 1

Contoh proyeksi vektor pada suatu sumbu.

Pada bidang koordinat O x y ditentukan titik M 1 (x 1, y 1). Perlu dibuat proyeksi pada O x dan O y untuk menggambarkan vektor jari-jari titik M 1. Kita memperoleh koordinat vektor (x 1, 0) dan (0, y 1).

Jika kita berbicara tentang proyeksi a → ke benda bukan nol b → atau proyeksi a → ke arah b → , maka yang kita maksud adalah proyeksi a → ke sumbu yang arahnya bertepatan b →. Proyeksi a → ke garis yang ditentukan oleh b → dilambangkan dengan n p b → a → → . Diketahui bahwa jika sudut antara a → dan b → , n p b → a → → dan b → dapat dianggap searah. Jika sudutnya tumpul, n p b → a → → dan b → berlawanan arah. Dalam situasi tegak lurus a → dan b →, dan a → adalah nol, maka proyeksi a → pada arah b → adalah vektor nol.

Karakteristik numerik dari proyeksi suatu vektor ke suatu sumbu adalah proyeksi numerik suatu vektor ke suatu sumbu tertentu.

Definisi 2

Proyeksi numerik vektor ke sumbu adalah bilangan yang sama dengan hasil kali panjang suatu vektor dan kosinus sudut antara vektor tersebut dan vektor yang menentukan arah sumbu.

Proyeksi numerik A B → ke L dilambangkan dengan n p L A B → , dan a → ke b → - n p b → a → .

Berdasarkan rumus tersebut, kita memperoleh n p b → a → = a → · cos a → , b → ^ , dimana a → adalah panjang vektor a → , a ⇀ , b → ^ adalah sudut antara vektor a → dan b → .

Kita memperoleh rumus untuk menghitung proyeksi numerik: n p b → a → = a → · cos a → , b → ^ . Ini berlaku untuk panjang a → dan b → dan sudut di antara keduanya yang diketahui. Rumus ini berlaku untuk koordinat a → dan b → yang diketahui, tetapi ada bentuk yang disederhanakan.

Contoh 2

Tentukan proyeksi numerik a → pada garis lurus searah b → dengan panjang a → sama dengan 8 dan sudut antara keduanya 60 derajat. Dengan syarat kita mempunyai a ⇀ = 8, a ⇀, b → ^ = 60°. Artinya kita substitusikan nilai numerik tersebut ke dalam rumus n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .

Menjawab: 4.

Dengan diketahui cos (a → , b → ^) = a ⇀ , b → a → · b → , kita mempunyai a → , b → sebagai hasil kali skalar dari a → dan b → . Mengikuti rumus n p b → a → = a → · cos a ⇀ , b → ^ , kita dapat mencari proyeksi numerik a → yang diarahkan sepanjang vektor b → dan mendapatkan n p b → a → = a → , b → b → . Rumusnya setara dengan definisi yang diberikan di awal paragraf.

Definisi 3

Proyeksi numerik vektor a → pada sumbu yang searah dengan b → adalah perbandingan hasil kali skalar vektor a → dan b → dengan panjangnya b → . Rumus n p b → a → = a → , b → b → dapat diterapkan untuk mencari proyeksi numerik a → pada garis yang searah dengan b → , yang diketahui koordinat a → dan b →.

Contoh 3

Diberikan b → = (- 3 , 4) . Temukan proyeksi numerik a → = (1, 7) ke L.

Larutan

Pada bidang koordinat n p b → a → = a → , b → b → berbentuk n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , dengan a → = (ax , a y ) dan b → = bx , oleh y . Untuk mencari proyeksi numerik vektor a → ke sumbu L, Anda memerlukan: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.

Menjawab: 5.

Contoh 4

Tentukan proyeksi a → pada L yang berimpit dengan arah b →, dimana terdapat a → = - 2, 3, 1 dan b → = (3, - 2, 6). Ruang tiga dimensi ditentukan.

Larutan

Diketahui a → = a x , a y , a z dan b → = b x , b y , b z , kita menghitung hasil kali skalar: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Panjang b → dicari menggunakan rumus b → = b x 2 + b y 2 + b z 2 . Maka rumus untuk menentukan proyeksi numerik a → adalah: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .

Substitusikan nilai numeriknya: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .

Jawaban: - 6 7.

Mari kita lihat hubungan antara a → di L dan panjang proyeksi a → di L. Mari kita menggambar sumbu L, menambahkan a → dan b → dari suatu titik di L, setelah itu kita menggambar garis tegak lurus dari ujung a → ke L dan menggambar proyeksi ke L. Ada 5 variasi gambar:

Pertama kasus dengan a → = n p b → a → → berarti a → = n p b → a → → , maka n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .

Kedua kasus tersebut menyiratkan penggunaan n p b → a → ⇀ = a → · cos a → , b → , yang artinya n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .

Ketiga kasus tersebut menjelaskan bahwa ketika n p b → a → → = 0 → kita memperoleh n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , maka n p b → a → → = 0 dan n p b → a → = 0 = n p b → a → → .

Keempat kasus menunjukkan n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , mengikuti n p b → a → = a → · cos ( a → , b → ^) = - n p b → a → → .

Kelima kasusnya menunjukkan a → = n p b → a → → , artinya a → = n p b → a → → , maka kita punya n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - a → = - n p b → a → .

Definisi 4

Proyeksi numerik vektor a → pada sumbu L, yang arahnya sama seperti b →, mempunyai nilai sebagai berikut:

• panjang proyeksi vektor a → ke L, dengan syarat sudut antara a → dan b → kurang dari 90 derajat atau sama dengan 0: n p b → a → = n p b → a → → dengan syarat 0 ≤ (a → , b →) ^< 90 ° ;
• nol dengan syarat a → dan b → tegak lurus: n p b → a → = 0, bila (a → , b → ^) = 90 °;
• panjang proyeksi a → ke L dikalikan -1, bila terdapat sudut tumpul atau lurus dari vektor a → dan b →: n p b → a → = - n p b → a → → dengan syarat 90°< a → , b → ^ ≤ 180 ° .

Contoh 5

Diketahui panjang proyeksi a → ke L, sama dengan 2. Temukan proyeksi numerik a → asalkan sudutnya 5 π 6 radian.

Larutan

Dari kondisi tersebut jelas bahwa sudut ini tumpul: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .

Jawaban: - 2.

Contoh 6

Diberikan sebuah bidang O x y z dengan panjang vektor a → sama dengan 6 3, b → (- 2, 1, 2) dengan sudut 30 derajat. Temukan koordinat proyeksi a → pada sumbu L.

Larutan

Pertama, kita menghitung proyeksi numerik vektor a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30° = 6 3 · 3 2 = 9 .

Syaratnya sudut lancip, maka proyeksi numerik a → = panjang proyeksi vektor a →: n p L a → = n p L a → → = 9. Kasus ini menunjukkan bahwa vektor n p L a → → dan b → berarah bersama, artinya ada bilangan t yang persamaannya benar: n p L a → → = t · b → . Dari sini kita melihat bahwa n p L a → → = t · b → , yang berarti kita dapat mencari nilai parameter t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .

Maka n p L a → → = 3 · b → dengan koordinat proyeksi vektor a → pada sumbu L sama dengan b → = (- 2 , 1 , 2) , dimana perlu mengalikan nilainya dengan 3. Kita punya n p L a → → = (- 6 , 3 , 6) . Jawaban: (- 6, 3, 6).

Penting untuk mengulangi informasi yang telah dipelajari sebelumnya tentang kondisi kolinearitas vektor.

Jika Anda melihat kesalahan pada teks, silakan sorot dan tekan Ctrl+Enter