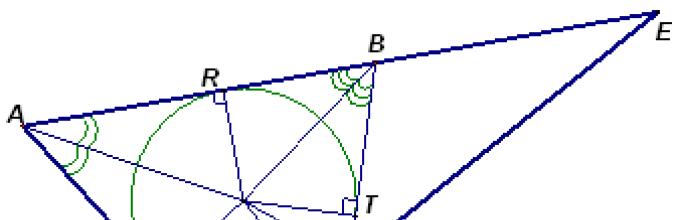
Paling sering memang demikian masalah geometri menimbulkan kesulitan bagi pelamar, lulusan, peserta olimpiade matematika. Jika melihat statistik UN Unified State tahun 2010, terlihat bahwa sekitar 12% peserta memulai soal geometri C4, dan hanya 0,2% peserta yang mendapat nilai penuh, dan secara umum soal tersebut ternyata adalah yang paling sulit dari semua yang diusulkan.
Jelasnya, semakin cepat kita menawarkan kepada anak-anak cara yang indah atau tidak terduga untuk memecahkan masalah, semakin besar kemungkinan mereka tertarik dan terpikat secara serius dan untuk waktu yang lama. Namun betapa sulitnya menemukan masalah yang menarik dan kompleks di tingkat kelas 7, ketika pembelajaran sistematis geometri baru dimulai. Apa yang dapat ditawarkan kepada siswa yang tertarik pada matematika yang hanya mengetahui tanda-tanda persamaan segitiga dan sifat-sifat sudut yang berdekatan dan vertikal? Namun, kita dapat memperkenalkan konsep garis singgung lingkaran, sebagai garis lurus yang memiliki satu titik persekutuan dengan lingkaran; Asumsikan bahwa jari-jari yang ditarik ke titik kontak tegak lurus terhadap garis singgung. Tentu saja, ada baiknya mempertimbangkan semua kemungkinan kasus susunan dua lingkaran dan garis singgung persekutuannya, yang dapat ditarik dari nol hingga empat. Dengan membuktikan teorema yang diajukan di bawah ini, Anda dapat memperluas rangkaian masalah secara signifikan untuk siswa kelas tujuh. Pada saat yang sama, buktikan secara bersamaan penting atau sekadar menarik dan fakta menyenangkan. Selain itu, karena banyak pernyataan yang tidak dimasukkan dalam buku teks sekolah, maka pernyataan tersebut dapat didiskusikan di kelas lingkaran dan dengan lulusan saat mengulang planimetri. Fakta-fakta ini ternyata relevan pada tahun ajaran lalu. Karena banyak diagnostik yang bekerja sendiri Pekerjaan Ujian Negara Bersatu berisi soal yang penyelesaiannya perlu menggunakan sifat ruas singgung yang dibuktikan di bawah ini.
T 1
Ruas garis singgung lingkaran diambil darinya
sama dengan satu titik (Gbr. 1)
Inilah teorema yang pertama kali bisa Anda perkenalkan kepada siswa kelas tujuh.
Dalam proses pembuktiannya, kita menggunakan tanda persamaan segitiga siku-siku dan menyimpulkan bahwa pusat lingkaran terletak pada garis bagi sudut. BSA.
Sepanjang perjalanan, kita ingat bahwa garis bagi suatu sudut adalah tempat kedudukan titik-titik di daerah dalam suatu sudut, yang berjarak sama dari sisi-sisinya. Solusi untuk masalah yang jauh dari sepele didasarkan pada fakta-fakta ini, yang dapat diakses bahkan oleh mereka yang baru mulai mempelajari geometri.

1. Pembagi sudut A, DI DALAM Dan DENGAN segi empat cembung ABCD berpotongan di satu titik. sinar AB Dan DC berpotongan di suatu titik E, dan sinarnya
Matahari Dan IKLAN pada intinya F. Buktikan bahwa segi empat tidak cembung AECF jumlah panjang sisi-sisi yang berhadapan adalah sama.
Solusi (Gbr. 2). Membiarkan TENTANG– titik potong garis-bagi ini. Kemudian TENTANG berjarak sama dari semua sisi segi empat ABCD, itu adalah
adalah pusat lingkaran pada segi empat. Menurut teorema 1
persamaan berikut ini benar: AR = AK.,
UGD = E.P., F.T. = FK. Mari kita jumlahkan ruas kiri dan kanan suku demi suku dan dapatkan persamaan yang benar:
(AR + UGD) + F.T. = (AK. +FK) + E.P.; A.E. + (FC + CT) = A.F. + (UE + komputer). Karena ST = RS, Itu AE + FC = A.F. + UE, itulah yang perlu dibuktikan.
Mari kita perhatikan suatu masalah dengan rumusan yang tidak biasa, yang penyelesaiannya cukup mengetahui teoremanya 1 .
2. Apakah ada N-segitiga yang sisi-sisinya berurutan 1, 2, 3, ..., N, ke dalam lingkaran manakah dapat ditulisi?
Larutan. Katakanlah ini N-gon ada. A 1 A 2 =1, …, A n-1 A n= N– 1,A N A 1 = N. B 1 , …, B n – titik kontak yang sesuai. Kemudian dengan Teorema 1 A 1 B 1 = A 1 B N< 1, N – 1 < A N B N< N. Berdasarkan sifat segmen singgung A N B n= A N B n-1. Tetapi, A N B n-1< A n-1 A n= N - 1. Kontradiksi. Oleh karena itu tidak N-gon memenuhi kondisi masalah.

T 2 Jumlah sisi-sisi berhadapan pada segiempat yang dijelaskan
lingkarannya sama besar (Gbr. 3)
Anak-anak sekolah, pada umumnya, dengan mudah membuktikan sifat segi empat yang dijelaskan ini. Setelah membuktikan teorema tersebut 1 , ini adalah latihan. Kita dapat menggeneralisasi fakta ini - jumlah sisi-sisi segitiga genap berbatas yang melalui salah satu sisinya adalah sama. Misalnya untuk segi enam ABCDEF Kanan: AB + CD + EF = BC + DE + FA.

Solusi (Gbr. 1). Karena segi empat ABEF dan ECDF bersifat siklik, maka menurut Teorema 2 P ABEF = 2(AB + EF) dan P ECDF = 2(CD + EF), dengan syarat
P ABEF – P ECDF = 2(AB + EF) – 2(CD + EF) = 2p. AB – CD = hal. AB = a + hal.

garis singgung lingkaran digambar memotong segmen-segmen tersebut AB Dan AC di poin M Dan R masing-masing. Buktikan keliling segitiga AMR dan besarnya sudut MPA tidak bergantung pada pilihan titik X.
Solusi (Gbr. 5). Menurut Teorema 1 MV = MX dan RS = RH. Oleh karena itu, keliling segitiga AMR sama dengan jumlah segmen AB Dan AC. Atau garis singgung ganda yang ditarik pada lingkaran luar suatu segitiga AMR . Nilai sudut MOP diukur setengah sudutnya VOS, yang tidak bergantung pada pilihan titik X.

Solusi (Gbr. 6). Metode satu (aljabar). Membiarkan AK = SEBUAH = x, Kemudian BK = BM = c – x, CM = CN = a – c + x. AC = SEBUAH + NC, maka kita dapat membuat persamaan untuk x: b = x + (a – c + x). Di mana
![]() .
.
Metode dua (geometris). Mari kita lihat diagramnya. Ruas-ruas garis singgung yang sama besar, diambil satu demi satu, dijumlahkan menjadi setengah keliling
segi tiga. Merah dan hijau membentuk satu sisi A. Lalu segmen yang kami minati x = hal – sebuah. Tentu saja hasil yang didapat bertepatan.


4. Tentukan jari-jari lingkaran pada segitiga siku-siku yang berkaki a, b dan sisi miring Dengan. Solusi (Gbr. 8). T oke bagaimana caranya OMCN- persegi, maka jari-jari lingkaran yang tertulis sama dengan garis singgung ruas CN.
![]() .
.


5. Buktikan bahwa titik singgung sisi bertulisan dan lingkaran dengan sisi segitiga adalah simetris terhadap titik tengah sisi tersebut.
Solusi (Gbr. 9). Perhatikan bahwa AK adalah ruas singgung lingkaran luar suatu segitiga ABC. Menurut rumus (2)
![]() . VM- segmen garis
bersinggungan dengan lingkaran dalam suatu segitiga ABC. Menurut rumus (1)
. VM- segmen garis
bersinggungan dengan lingkaran dalam suatu segitiga ABC. Menurut rumus (1)
![]() . AK = VM, dan ini berarti poinnya K dan M berjarak sama dari tengah sisi AB, Q.E.D.
. AK = VM, dan ini berarti poinnya K dan M berjarak sama dari tengah sisi AB, Q.E.D.

6. Dua garis singgung persekutuan luar dan satu garis singgung dalam digambarkan pada dua lingkaran. Garis singgung dalam memotong garis singgung luar pada titik-titik A, B dan menyentuh lingkaran pada titik-titiknya Sebuah 1 Dan DALAM 1 . Buktikan itu AA 1 = BB 1.
Solusi (Gbr. 10). Berhenti... Apa yang harus diputuskan? Ini hanyalah rumusan yang berbeda dari permasalahan sebelumnya. Jelasnya, salah satu lingkaran bertuliskan dan yang lainnya merupakan lingkaran luar untuk segitiga tertentu ABC. Dan segmennya AA 1 dan BB 1 sesuai dengan segmen AK Dan VM tugas 5. Patut dicatat bahwa tugas yang diusulkan di Olimpiade Seluruh Rusia anak sekolah dalam matematika, diselesaikan dengan cara yang begitu jelas.

7. Sisi-sisi segi lima menurut urutan lintasannya adalah 5, 6, 10, 7, 8. Buktikan bahwa lingkaran tidak dapat ditulisi pada segi lima tersebut.
Solusi (Gbr. 11). Misalkan dalam segi lima ABCDE Anda bisa menulis lingkaran. Apalagi para pihak AB, SM, CD, DE Dan EA masing-masing sama dengan 5, 6, 10, 7 dan 8. Mari kita tandai titik singgungnya secara berurutan – F, G, H, M Dan N. Biarkan panjang segmennya A.F. sama dengan X.
Kemudian BF = FD – A.F. = 5 – X = BG. GC = SM – BG = = 6 – (5 – X) = 1 + X = CH. Dan seterusnya: HD = DM = 9 – X; AKU. = EN = X – 2, SEBUAH = 10 – X.
Tetapi, A.F. = SEBUAH. Itu adalah 10 - X = X; X= 5. Namun ruas singgungnya A.F. tidak bisa sama sisi AB. Kontradiksi yang dihasilkan membuktikan bahwa sebuah lingkaran tidak dapat dituliskan dalam segi lima tertentu.
8. Sebuah lingkaran terletak di dalam segi enam, sisi-sisinya menurut urutan kelilingnya adalah 1, 2, 3, 4, 5. Tentukan panjang sisi keenamnya.
Larutan. Tentu saja kita dapat menetapkan segmen singgung sebagai X, seperti pada soal sebelumnya, buat persamaan dan dapatkan jawabannya. Namun, akan jauh lebih efisien dan efektif jika menggunakan catatan teorema 2 : jumlah sisi-sisi segi enam yang dibatasi, yang melalui satu sama lain, adalah sama.
Maka 1+3+5 = 2+4+ X, Di mana X– sisi keenam yang tidak diketahui, X = 3.

Solusi (Gbr. 12). Karena panjang semua sisinya adalah bilangan bulat, maka bagian pecahan dari panjang segmennya adalah sama BT, BP, DM, hari, AK. Dan PADA. Kita punya PADA + televisi= 1, dan bagian pecahan dari panjang segmen PADA Dan TBC adalah sama. Hal ini hanya mungkin terjadi bila PADA + televisi= 0,5. Menurut teorema 1
VT + VR.
Cara, VR= 0,5. Perhatikan kondisinya CD= 3 ternyata tidak diklaim. Jelasnya, penulis masalah ini menyarankan solusi lain. Jawaban: 0,5.

10. Dalam segi empat ABCD IKLAN = DC, AB = 3, BC = 5. Lingkaran bertuliskan segitiga ABD Dan CBD menyentuh satu segmen BD di poin M Dan N masing-masing. Temukan panjang segmen tersebut M N.
Solusi (Gbr. 13). MN = DN – DM. Menurut rumus (1) untuk segitiga DBA Dan DBC oleh karena itu, kami memiliki:

11. Menjadi segi empat ABCD Anda bisa menulis lingkaran. Lingkaran bertuliskan segitiga ABD Dan CBD memiliki jari-jari R Dan R masing-masing. Temukan jarak antara pusat lingkaran ini.
Solusi (Gbr. 13). Karena dengan syarat segi empat ABCD tertulis, berdasarkan teorema 2 kita punya: AB + DC = IKLAN + SM. Mari kita gunakan ide untuk memecahkan masalah sebelumnya. . Artinya titik singgung lingkaran dengan ruas DM sesuai. Jarak antara pusat lingkaran sama dengan jumlah jari-jarinya. Menjawab: R+r.
Faktanya, kondisi tersebut terbukti berbentuk segi empat ABCD Anda dapat menuliskan lingkaran, setara dengan kondisi - di segi empat cembung ABCD lingkaran bertuliskan segitiga ABC Dan ADC saling menyentuh. Yang terjadi justru sebaliknya.
Diusulkan untuk membuktikan kedua pernyataan yang saling bertolak belakang ini dalam soal berikut, yang dapat dianggap sebagai generalisasi dari soal ini.

12. Pada segiempat cembung ABCD (beras. 14) lingkaran bertuliskan segitiga ABC Dan ADC saling menyentuh. Buktikan bahwa lingkaran terdapat pada segitiga ABD Dan BDC juga saling menyentuh.

13. Dalam segitiga ABC dengan para pihak a, b Dan C di sisi Matahari titik yang ditandai D sehingga lingkaran-lingkaran itu tertulis dalam segitiga ABD Dan ACD menyentuh satu segmen IKLAN di satu titik. Temukan panjang segmen tersebut BD.
Solusi (Gbr. 15). Mari kita terapkan rumus (1) untuk segitiga ADC Dan A.D.B., menghitung DM dua 
Ternyata, D– titik kontak dengan samping Matahari lingkaran tertulis dalam segitiga ABC. Yang terjadi adalah sebaliknya: jika titik sudut suatu segitiga dihubungkan dengan titik singgung lingkaran pada sisi yang berhadapan, maka lingkaran-lingkaran pada segitiga yang dihasilkan saling bersentuhan.

14. Pusat TENTANG 1 , TENTANG 2 dan TENTANG 3 Tiga buah lingkaran yang tidak berpotongan dan berjari-jari sama terletak pada titik sudut suatu segitiga. Dari poin TENTANG 1 , TENTANG 2 , TENTANG 3, garis singgung lingkaran tersebut digambar seperti pada gambar.
Diketahui bahwa garis singgung ini, berpotongan, membentuk segi enam cembung, yang sisi-sisinya dicat merah dan biru. Buktikan bahwa jumlah panjang ruas berwarna merah sama dengan jumlah panjang ruas berwarna biru.
Solusi (Gbr. 16). Penting untuk memahami cara menggunakan fakta bahwa lingkaran tertentu memiliki jari-jari yang sama. Perhatikan bahwa segmennya Br Dan DM adalah sama, yang mengikuti persamaan segitiga siku-siku TENTANG 1 Br Dan HAI 2 B.M.. Juga D.L. = D.P., FN = FK. Kita menjumlahkan persamaan suku demi suku, lalu mengurangi dari jumlah yang dihasilkan segmen garis singgung identik yang ditarik dari simpul-simpulnya A, DENGAN, Dan E segi enam ABCDEF: AR Dan AK., C.L. Dan CM, EN Dan E.P.. Kami mendapatkan apa yang kami butuhkan.
Berikut adalah contoh soal stereometri yang diajukan pada Turnamen Matematika Internasional XII untuk Siswa Sekolah Menengah Atas “Piala Mengenang A. N. Kolmogorov”.
16. Diberikan sebuah piramida segi lima SA 1 SEBUAH 2 SEBUAH 3 SEBUAH 4 SEBUAH 5 . Ada sebuah bola w, yang menyentuh seluruh tepi piramida dan bola lainnya w 1, yang menyentuh seluruh sisi alasnya SEBUAH 1 SEBUAH 2 SEBUAH 3 SEBUAH 4 SEBUAH 5 dan kelanjutan tulang rusuk lateral SA 1, SA 2, SA 3, SA 4, SA 5 melampaui puncak pangkalan. Buktikan bahwa puncak limas mempunyai jarak yang sama dari simpul alasnya. (Berlov S.L., Karpov D.V.)

karena ruas garis singgungnya sama besar. Membiarkan C saya A saya = a saya. Kemudian hal SAiAi +1 = s+a saya +ai+1, dan dari persamaan keliling maka berikut ini A 1 = A 3 = A 5 = A 2 = A 4, dari mana S.A. 1 = S.A. 2 = S.A. 3 = S.A. 4 = S.A. 5 .
17. Ujian Negara Bersatu. Pekerjaan diagnostik 8.12.2009, S–4. Diberikan sebuah trapesium ABCD, yang fondasinya SM = 44,IKLAN = 100, AB = CD= 35. Lingkaran bersinggungan dengan garis IKLAN Dan AC, menyentuh samping CD pada intinya K. Temukan panjang segmen tersebut CK.BDC dan BDA, sentuh bagian samping ВD di poin E Dan F. Temukan panjang segmen tersebut E.F..
Larutan. Ada dua kasus yang mungkin terjadi (Gbr. 20 dan Gbr. 21). Dengan menggunakan rumus (1) kita mencari panjang ruas-ruas tersebut DE Dan DF.

Dalam kasus pertama IKLAN = 0,1AC, CD = 0,9AC. Yang kedua - IKLAN = 0,125AC, CD = 1,125AC. Kami mengganti data dan mendapatkan jawabannya: 4.6 atau 5.5.
Masalah untuk solusi mandiri/

1. Keliling trapesium sama kaki yang dibatasi pada lingkaran adalah sama dengan 2 gosok. Temukan proyeksi diagonal trapesium ke alas yang lebih besar. (1/2r)
2. Bank terbuka Masalah Ujian Negara Bersatu matematika. JAM 4. Ke lingkaran tertulis dalam segitiga ABC (Gbr. 22), tiga garis singgung ditarik. Keliling segitiga yang dipotong adalah 6, 8, 10. Tentukan keliling segitiga tersebut. (24)
3. Menjadi segitiga ABC lingkaran tertulis. M N - bersinggungan dengan lingkaran, MÎ AC, NÎ BC, BC = 13, AC = 14, AB = 15. Temukan keliling segitiga perusahaan multinasional. (12)
4. Pada sebuah lingkaran yang berbentuk persegi dengan sisi a, ditarik garis singgung yang memotong kedua sisinya. Temukan keliling segitiga yang dipotong. (A)
5. Sebuah lingkaran terdapat pada segi lima yang mempunyai sisi-sisinya A, D, C, D Dan e. Temukan segmen yang titik singgungnya membagi sisi sama besar A.
6. Sebuah lingkaran terdapat pada segitiga dengan sisi 6, 10 dan 12. Sebuah lingkaran ditarik garis singgung sehingga memotong dua sisi panjangnya. Temukan keliling segitiga yang dipotong. (16)
7. CD– median segitiga ABC. Lingkaran bertuliskan segitiga ACD Dan BCD, sentuh segmen tersebut CD di poin M Dan N. Menemukan M N, Jika AC – Matahari = 2. (1)
8. Dalam segitiga ABC dengan para pihak a, b Dan C di sisi Matahari titik yang ditandai D. Untuk lingkaran bertuliskan segitiga ABD Dan ACD, garis singgung persekutuan ditarik berpotongan IKLAN pada intinya M. Temukan panjang segmen tersebut SAYA. (Panjang SAYA tidak bergantung pada posisi titik tersebut D Dan
sama dengan ½ ( c + b – sebuah))
9.B segitiga siku-siku tertulis dalam lingkaran berjari-jari A. Jari-jari lingkaran yang bersinggungan dengan sisi miring dan perpanjangan kaki-kakinya adalah sama R. Temukan panjang sisi miringnya. ( R–a)
10. Dalam segitiga ABC diketahui panjang sisinya: AB = Dengan, AC = B, Matahari = A. Sebuah lingkaran pada segitiga menyentuh salah satu sisinya AB pada intinya C 1. Lingkaran luar menyentuh perpanjangan sisi AB per poin A pada intinya dari 2. Tentukan panjang segmen tersebut C 1 C 2. (B)
11. Tentukan panjang sisi-sisi segitiga dibagi titik singgung lingkaran berjari-jari 3 cm menjadi ruas-ruas 4 cm dan 3 cm (7, 24 dan 25 cm pada segitiga siku-siku)
12. Olimpiade Soros 1996, babak ke-2, kelas 11. Diberikan sebuah segitiga ABC, di sisinya titik-titiknya ditandai SEBUAH 1, B 1, C 1. Jari-jari lingkaran bertuliskan segitiga AC 1 B 1, BC 1 A 1, SA 1 B 1 sama di R. Jari-jari lingkaran pada segitiga A 1 B 1 C 1 sama R. Temukan jari-jari lingkaran yang terdapat dalam segitiga ABC. (R +R).
Soal 4–8 diambil dari buku soal RK Gordin “Geometri. Planimetri." Moskow. Penerbitan MCNMO. 2004.
Bukti
Jika tali busur adalah diameter, maka teoremanya jelas.
Gambar 287 menunjukkan sebuah lingkaran dengan pusat O, M adalah titik potong diameter CD dan tali busur AB, CD ⊥ AB. Kita perlu membuktikan bahwa AM = MB.
Mari kita menggambar jari-jari OA dan OB. DI DALAM segitiga sama kaki Segmen AOB (OA = OB) OM adalah tinggi, dan karenanya median, yaitu AM = MB.
Teorema 20.2
Diameter lingkaran yang membagi tali busur selain diameternya menjadi dua adalah tegak lurus terhadap tali busur tersebut.
Buktikan sendiri teorema ini. Pertimbangkan apakah pernyataan ini benar jika tali busur adalah diameter.
Gambar 288 menunjukkan semua kemungkinan kasus posisi relatif garis lurus dan lingkaran. Pada Gambar 288, a mereka tidak memiliki titik persekutuan, pada Gambar 288, b - mereka memiliki dua poin umum, pada Gambar 288, dalam - satu.
|
Beras. 288 |
||
|
|
|
|
Definisi
Garis lurus yang hanya mempunyai satu titik persekutuan dengan lingkaran disebut garis singgung lingkaran.
Garis singgung lingkaran hanya mempunyai satu titik persekutuan dengan lingkaran yang dibatasi oleh lingkaran tersebut. Pada Gambar 288 garis a bersinggungan dengan lingkaran yang berpusat di titik O, A adalah titik singgungnya.
Jika suatu ruas (sinar) bersinggungan dengan lingkaran dan mempunyai titik persekutuan dengan lingkaran tersebut, maka ruas (sinar) tersebut dikatakan bersinggungan dengan lingkaran. Misalnya Gambar 289 menunjukkan ruas AB yang menyentuh lingkaran di titik C.
Teorema 20.3
(properti tangen)
Garis singgung lingkaran tegak lurus terhadap jari-jari yang ditarik ke titik singgung tersebut.
Bukti
Gambar 290 menunjukkan sebuah lingkaran dengan pusat O, A adalah titik singgung antara garis lurus a dan lingkaran. Kita perlu membuktikan bahwa OA ⊥ a.
|
Beras. 289 |
Beras. 290 |
Beras. 291 |
|
|
|
|
Misalkan tidak demikian, yaitu ruas OA condong ke garis lurus a. Kemudian dari titik O kita turunkan garis tegak lurus OM ke garis lurus a (Gbr. 291). Karena titik A merupakan satu-satunya titik persekutuan antara garis a dan lingkaran yang berpusat di O, maka titik M tidak termasuk dalam lingkaran tersebut. Jadi OM = MB + OB, dimana titik B adalah titik potong lingkaran dan tegak lurus OM. Ruas OA dan OB sama besar dengan jari-jari lingkaran. Jadi OM > OA. Kami memperoleh kontradiksi: OM yang tegak lurus lebih besar dari OA yang miring. Oleh karena itu, OA ⊥ a.
Teorema 20.4
(tanda garis singgung lingkaran)
Jika suatu garis lurus yang melalui suatu titik pada suatu lingkaran tegak lurus dengan jari-jari yang ditarik ke titik tersebut, maka garis lurus tersebut bersinggungan dengan lingkaran tersebut.
Bukti
|
Beras. 292 |
|
|
Gambar 290 menunjukkan sebuah lingkaran yang berpusat di titik O, ruas OA adalah jari-jarinya, titik A termasuk dalam garis a, OA ⊥ a. Mari kita buktikan bahwa garis a bersinggungan dengan lingkaran.
Misalkan garis lurus a tidak bersinggungan, tetapi mempunyai titik persekutuan lain B dengan lingkaran (Gbr. 292). Maka ∆ AOB adalah sama kaki (OA = OB sebagai jari-jari). Jadi ∠ OBA = ∠ OAB = 90°. Kita mendapatkan kontradiksi: segitiga AOB memiliki dua sudut siku-siku. Jadi garis a bersinggungan dengan lingkaran.
Konsekuensi
Jika jarak pusat lingkaran ke suatu garis lurus tertentu sama dengan jari-jari lingkaran, maka garis lurus tersebut bersinggungan dengan lingkaran tersebut.
|
Beras. 293 |
|
|
Buktikan sendiri akibat wajar ini.
Tugas. Buktikan jika melalui titik ini dua garis singgung ditarik pada sebuah lingkaran, maka ruas garis singgung yang menghubungkan suatu titik tertentu dengan titik singgung tersebut adalah sama besar.
Larutan. Gambar 293 menunjukkan sebuah lingkaran dengan pusat O. Garis AB dan AC merupakan garis singgung, titik B dan C merupakan titik singgung. Kita perlu membuktikan bahwa AB = AC.
Mari kita tarik jari-jari OB dan OC ke titik-titik kontak. Berdasarkan sifat singgungnya, OB ⊥ AB dan OC ⊥ AC. Pada segitiga siku-siku AOB dan AOC, kaki-kaki OB dan OC sama besar dengan jari-jari satu lingkaran, AO adalah sisi miring persekutuan. Oleh karena itu, segitiga AOB dan AOC mempunyai sisi miring dan kaki yang sama besar. Jadi AB = AC.

- Bagaimana diameter tegak lurus membagi tali busur?
- Berapakah sudut antara tali busur selain diameter dan diameter yang membagi tali busur tersebut menjadi dua?
- Jelaskan semua kemungkinan kasus posisi relatif garis dan lingkaran.
- Garis apa yang disebut garis singgung lingkaran?
- Sifat apa yang dimiliki jari-jari yang ditarik ke titik singgung garis dan lingkaran?
- Merumuskan uji garis singgung lingkaran.
- Sifat apa yang dimiliki garis singgung lingkaran melalui satu titik?

Tugas praktis

507. Gambarlah sebuah lingkaran dengan pusat O, gambarlah tali busur AB. Dengan menggunakan persegi, bagilah tali busur ini menjadi dua.
508. Gambarlah sebuah lingkaran dengan pusat O, gambarlah tali busur CD. Dengan menggunakan penggaris berskala, gambarlah diameter yang tegak lurus terhadap tali busur CD.
509. Gambarlah sebuah lingkaran, tandai titik A dan B di atasnya.Dengan menggunakan penggaris dan persegi, gambarlah garis lurus yang menyentuh lingkaran di titik A dan B.
510. Gambarlah garis a dan tandai titik M. Dengan menggunakan persegi, penggaris, dan kompas, gambarlah sebuah lingkaran berjari-jari 3 cm yang menyentuh garis a di titik M. Berapa banyak lingkaran yang dapat dibuat?

Latihan
511. Pada Gambar 294, titik O merupakan pusat lingkaran, diameter CD tegak lurus tali busur AB. Buktikan bahwa ∠AOD = ∠BOD.
512. Buktikan bahwa tali busur yang sama panjang pada suatu lingkaran mempunyai jarak yang sama dari pusatnya.
513. Buktikan bahwa jika tali busur suatu lingkaran mempunyai jarak yang sama dari pusatnya, maka kedua tali busur tersebut sama besar.
514. Benarkah garis lurus yang tegak lurus jari-jari lingkaran menyentuh lingkaran tersebut?
515. Lurus CD menyentuh sebuah lingkaran yang berpusat O di titik A, ruas AB adalah tali busur lingkaran, ∠ BAD = 35° (Gbr. 295). Temukan ∠AOB.
516. Lurus CD menyentuh sebuah lingkaran yang berpusat O di titik A, ruas AB adalah tali busur lingkaran, ∠ AOB = 80° (lihat Gambar 295). Temukan ∠BAC.
517. Diberikan sebuah lingkaran yang diameternya 6 cm, Garis a dikeluarkan dari pusatnya sebesar: 1) 2 cm; 2) 3cm; 3) 6 cm Berapakah garis singgung lingkaran?
518. Pada segitiga ABC kita mengetahui bahwa ∠ C = 90°. Buktikan bahwa:
1) lurus BC bersinggungan dengan lingkaran yang pusat A melalui titik C;
2) lurus AB tidak bersinggungan dengan lingkaran yang berpusat C melalui titik A.

519. Buktikan bahwa diameter sebuah lingkaran lebih besar dari tali busur manapun selain diameternya.
520. Pada lingkaran dengan pusat O, tali busur AB ditarik melalui titik tengah jari-jarinya, tegak lurus terhadap lingkaran tersebut. Buktikan bahwa ∠ AOB = 120°.
521. Tentukan sudut antara jari-jari OA dan OB lingkaran jika jarak pusat O lingkaran ke tali busur AB 2 kali lebih kecil dari: 1) panjang tali busur AB; 2) jari-jari lingkaran.
522. Diameter AB dan tali busur AC dan CD digambarkan membentuk lingkaran sehingga AC = 12 cm, ∠ BAC = 30°, AB ⊥ CD. Carilah panjang akord CD.
523. Melalui intinya M pada lingkaran yang berpusat O kita tarik garis singgung MA dan MB, A dan B merupakan titik singgung, ∠ OAB = 20°. Temukan ∠AMB.
524. Melalui ujung-ujung tali busur AB yang sama dengan jari-jari lingkaran, ditarik dua garis singgung yang berpotongan di titik C. Tentukan ACB.
525. Melalui intinya Dari sebuah lingkaran yang berpusat di O kita tarik garis singgung lingkaran tersebut, AB adalah diameter lingkaran tersebut. Dari titik A sebuah AD yang tegak lurus dijatuhkan pada suatu garis singgung. Buktikan bahwa sinar AC merupakan garis bagi sudut BAD.
526. Lurus AC menyentuh lingkaran dengan pusat O di titik A (Gbr. 296). Buktikan bahwa sudut BAC 2 kali lebih kecil dari sudut AOB.
|
Beras. 294 |
Beras. 295 |
Beras. 296 |
|
|
|
|
527. Segmen AB dan BC berturut-turut adalah tali busur dan diameter lingkaran, ∠ ABC = 30°. Melalui titik A, tarik garis singgung lingkaran yang memotong garis BC di titik D. Buktikan bahwa ABD sama kaki.
528. Diketahui diameter AB membagi dua tali busur CD, tetapi tidak tegak lurus terhadap tali tersebut. Buktikan bahwa CD juga merupakan diameter.

529. Temukan tempat kedudukan pusat lingkaran yang menyentuh garis tertentu pada suatu titik tertentu.
530. Temukan tempat kedudukan pusat lingkaran yang menyentuh kedua sisi sudut tertentu.
531. Temukan tempat kedudukan pusat lingkaran yang menyentuh garis tertentu.
532. Garis singgung lingkaran yang berpusat O di titik A dan B berpotongan di titik K, ∠ AKB = 120°. Buktikan AK + BK = OK.
533. Lingkaran menyentuh sisi AB segitiga ABC di titik M dan menyentuh perpanjangan kedua sisi lainnya. Buktikan bahwa jumlah panjang ruas BC dan BM sama dengan setengah keliling segitiga ABC.
|
Beras. 297 |
|
|
534. Melalui intinya C adalah garis singgung AC dan BC pada lingkaran, A dan B adalah titik singgung (Gbr. 297). Pada lingkaran kita mengambil titik sembarang M yang terletak pada setengah bidang yang sama dengan titik C relatif terhadap garis AB, dan melalui titik tersebut kita menggambar garis singgung lingkaran yang memotong garis AC dan BC masing-masing di titik D dan E. Buktikan bahwa keliling segitiga DEC tidak bergantung pada pilihan titik M.
Latihan untuk diulang
535. Buktikan bahwa titik tengah M suatu segmen yang ujung-ujungnya terdapat pada dua garis sejajar adalah titik tengah setiap segmen yang melalui titik M dan ujung-ujungnya termasuk dalam garis-garis tersebut.
536. Segmen AB dan CD terletak pada garis yang sama dan mempunyai titik tengah yang sama. Titik M dipilih agar segitiga AMB sama kaki dengan alas AB. Buktikan bahwa ∆ CMD juga sama kaki dengan CD dasar.
537. Di sisi MK segitiga MPK diberi tanda titik E dan F sehingga titik E terletak di antara titik M dan F, ME = EP, PF = FK. Tentukan sudut M jika ∠ EPF = 92°, ∠ K = 26°.
538. DI DALAM segitiga lancip ABC, ditarik garis bagi BM, ditarik garis tegak lurus MK dari titik M ke sisi BC, ∠ ABM = ∠ KMC. Buktikan itu segitiga ABC- sama kaki.
Amati, gambar, desain, berfantasi
539. Tetapkan pola bentuk gambar yang ditunjukkan pada Gambar 298. Gambar manakah yang harus ditempatkan selanjutnya?
|
Beras. 298 |
Garis potong, garis singgung - semua ini dapat didengar ratusan kali dalam pelajaran geometri. Namun kelulusan sekolah telah berlalu, tahun-tahun berlalu, dan semua pengetahuan ini terlupakan. Apa yang harus kamu ingat?
Esensi
Istilah “singgung lingkaran” mungkin sudah tidak asing lagi bagi semua orang. Namun kecil kemungkinannya semua orang bisa dengan cepat merumuskan definisinya. Sedangkan garis singgung adalah garis lurus yang terletak pada bidang yang sama dengan lingkaran dan hanya memotongnya di satu titik. Jumlahnya mungkin sangat banyak, tapi semuanya punya properti yang identik, yang akan dibahas di bawah ini. Seperti yang bisa Anda tebak, titik singgung adalah tempat perpotongan lingkaran dan garis lurus. Dalam setiap kasus tertentu hanya ada satu, tetapi jika lebih banyak, maka itu akan menjadi garis potong.
Sejarah penemuan dan studi
Konsep garis singgung muncul pada zaman dahulu. Konstruksi garis lurus ini, pertama menjadi lingkaran, kemudian menjadi elips, parabola, dan hiperbola dengan menggunakan penggaris dan kompas, telah dilakukan sejak dahulu kala. tahap awal perkembangan geometri. Tentu saja sejarah tidak menyimpan nama penemunya, namun ternyata pada saat itu masyarakat sudah cukup familiar dengan sifat-sifat garis singgung lingkaran.
Di zaman modern, minat terhadap fenomena ini kembali berkobar - babak baru studi konsep ini dimulai, dikombinasikan dengan penemuan kurva baru. Jadi, Galileo memperkenalkan konsep sikloid, dan Fermat serta Descartes membangun garis singgungnya. Sedangkan untuk lingkaran, sepertinya tidak ada rahasia yang tersisa bagi orang dahulu di kawasan ini.
Properti
Jari-jari yang ditarik ke titik potong adalah Ini
sifat utama, tetapi bukan satu-satunya sifat yang dimiliki garis singgung lingkaran. Fitur penting lainnya mencakup dua garis lurus. Jadi, melalui satu titik yang terletak di luar lingkaran, dapat ditarik dua garis singgung, dan segmen-segmennya akan sama panjang. Ada teorema lain tentang topik ini, tetapi jarang dibahas dalam kerangka standar kursus sekolah, meskipun sangat berguna untuk memecahkan beberapa masalah. Kedengarannya seperti ini. Dari satu titik yang terletak di luar lingkaran, ditarik garis singgung dan garis potong padanya. Ruas AB, AC dan AD terbentuk. A adalah perpotongan garis, B adalah titik singgung, C dan D adalah perpotongan. Dalam hal ini, persamaan berikut akan berlaku: panjang garis singgung lingkaran, kuadrat, akan sama dengan hasil kali segmen AC dan AD.
Ada konsekuensi penting dari hal di atas. Untuk setiap titik pada lingkaran, Anda dapat membuat garis singgung, tetapi hanya satu. Buktinya cukup sederhana: secara teoritis dengan menjatuhkan tegak lurus dari jari-jari ke atasnya, kita menemukan bahwa segitiga yang terbentuk tidak mungkin ada. Artinya garis singgungnya adalah satu-satunya.
Konstruksi
Di antara masalah-masalah lain dalam geometri, biasanya tidak ada kategori khusus

dicintai oleh murid-murid dan pelajar. Untuk menyelesaikan soal pada kategori ini, Anda hanya membutuhkan kompas dan penggaris. Ini adalah tugas konstruksi. Ada juga yang untuk membuat garis singgung.
Jadi, diberikan sebuah lingkaran dan sebuah titik yang terletak di luar batasnya. Dan kita perlu menarik garis singgung melaluinya. Bagaimana cara melakukannya? Pertama-tama, Anda perlu menggambar segmen antara pusat lingkaran O dan suatu titik tertentu. Kemudian gunakan kompas untuk membaginya menjadi dua. Untuk melakukan ini, Anda perlu mengatur radius - sedikit lebih dari setengah jarak antara pusat lingkaran asli dan titik ini. Setelah ini, Anda perlu membuat dua busur yang berpotongan. Selain itu, jari-jari kompas tidak perlu diubah, dan pusat setiap bagian lingkaran masing-masing akan menjadi titik awal dan O. Persimpangan busur harus dihubungkan, yang akan membagi segmen menjadi dua. Tetapkan radius pada kompas sama dengan jarak ini. Selanjutnya, buatlah lingkaran lain dengan pusat di titik potong. Titik asal dan O akan terletak di atasnya. Dalam hal ini, akan ada dua perpotongan lagi dengan lingkaran yang diberikan dalam soal. Mereka akan menjadi titik kontak untuk titik yang ditentukan pada awalnya.
Konstruksi garis singgung lingkaran itulah yang menyebabkan kelahiran

kalkulus diferensial. Karya pertama tentang topik ini diterbitkan oleh matematikawan terkenal Jerman Leibniz. Ini memberikan kemungkinan untuk menemukan maksimum, minimum dan garis singgung terlepas dari besaran pecahan dan irasional. Nah, sekarang digunakan untuk banyak perhitungan lainnya.
Selain itu, garis singgung lingkaran juga berkaitan dengan arti geometri garis singgung. Dari sinilah namanya berasal. Diterjemahkan dari bahasa Latin tangens berarti “singgung”. Dengan demikian, konsep ini tidak hanya dikaitkan dengan geometri dan kalkulus diferensial, tetapi juga dengan trigonometri.
Dua lingkaran
Garis singgung tidak selalu mempengaruhi hanya satu angka saja. Jika banyak garis lurus dapat ditarik pada satu lingkaran, mengapa tidak sebaliknya? Bisa. Namun tugas dalam kasus ini menjadi sangat rumit, karena garis singgung dua lingkaran mungkin tidak melalui titik mana pun, dan posisi relatif dari semua gambar ini bisa sangat besar.

berbeda.
Jenis dan varietas
Ketika kita berbicara tentang dua lingkaran dan satu atau lebih garis lurus, meskipun diketahui bahwa keduanya bersinggungan, tidak segera jelas bagaimana letak semua bangun tersebut dalam hubungannya satu sama lain. Berdasarkan hal ini, beberapa varietas dibedakan. Jadi, lingkaran mungkin memiliki satu atau dua titik yang sama atau tidak memilikinya sama sekali. Dalam kasus pertama mereka akan berpotongan, dan dalam kasus kedua mereka akan bersentuhan. Dan di sini ada dua varietas yang dibedakan. Jika satu lingkaran seolah-olah tertanam di lingkaran kedua, maka singgungannya disebut internal, jika tidak, maka eksternal. Anda dapat memahami posisi relatif bangun-bangun tidak hanya berdasarkan gambar, tetapi juga memiliki informasi tentang jumlah jari-jarinya dan jarak antara pusat-pusatnya. Jika kedua besaran tersebut sama, maka kedua lingkaran tersebut bersentuhan. Jika yang pertama lebih besar maka keduanya berpotongan, dan jika lebih kecil maka keduanya tidak mempunyai titik persekutuan.
Hal yang sama berlaku untuk garis lurus. Untuk dua lingkaran mana pun yang tidak memiliki titik persekutuan, Anda bisa melakukannya

buatlah empat garis singgung. Dua di antaranya akan berpotongan di antara gambar-gambar tersebut, disebut internal. Beberapa lainnya bersifat eksternal.
Jika kita berbicara tentang lingkaran yang memiliki satu titik persekutuan, maka masalahnya menjadi lebih sederhana. Intinya adalah apapun yang terjadi posisi relatif dalam hal ini mereka hanya memiliki satu garis singgung. Dan itu akan melewati titik perpotongannya. Jadi konstruksinya tidak akan sulit.
Jika bangun-bangun tersebut mempunyai dua titik potong, maka dapat dibuat garis lurus untuk bangun-bangun tersebut, bersinggungan dengan lingkaran yang satu dan yang lainnya, tetapi hanya bagian luarnya. Solusi untuk masalah ini mirip dengan apa yang akan dibahas di bawah ini.
Penyelesaian masalah
Garis singgung dalam dan luar dua lingkaran tidak mudah dibuat, meskipun masalah ini dapat diselesaikan. Faktanya adalah figur tambahan digunakan untuk ini, jadi Anda harus membuat metode ini sendiri

cukup bermasalah. Jadi, diberikan dua lingkaran dengan jari-jari dan pusat yang berbeda O1 dan O2. Bagi mereka, Anda perlu membuat dua pasang garis singgung.
Pertama-tama, Anda perlu membuat lingkaran tambahan di dekat pusat lingkaran yang lebih besar. Dalam hal ini, perbedaan antara jari-jari kedua angka awal harus ditentukan pada kompas. Garis singgung lingkaran bantu dibuat dari pusat lingkaran yang lebih kecil. Setelah itu, garis tegak lurus ditarik dari O1 dan O2 ke garis-garis tersebut hingga berpotongan dengan gambar aslinya. Sebagai berikut dari sifat dasar garis singgung, ditemukan titik-titik yang diperlukan pada kedua lingkaran. Masalahnya terpecahkan, setidaknya bagian pertama.
Untuk membangun garis singgung internal, Anda harus menyelesaikannya secara praktis

tugas serupa. Sekali lagi Anda memerlukan angka bantu, tetapi kali ini jari-jarinya akan sama dengan jumlah jari-jari aslinya. Garis singgung dibuat dari pusat salah satu lingkaran ini. Solusi selanjutnya dapat dipahami dari contoh sebelumnya.
Garis singgung pada sebuah lingkaran atau bahkan dua lingkaran atau lebih tidaklah demikian tugas yang sulit. Tentu saja, matematikawan sudah lama berhenti memecahkan masalah seperti itu secara manual dan mengandalkan perhitungan program khusus. Namun jangan berpikir bahwa sekarang Anda tidak harus bisa melakukannya sendiri, karena untuk merumuskan tugas komputer dengan benar, Anda perlu melakukan dan memahami banyak hal. Sayangnya, ada kekhawatiran bahwa setelah transisi terakhir ke bentuk tes pengendalian pengetahuan, tugas konstruksi akan semakin menimbulkan kesulitan bagi siswa.
Sedangkan untuk mencari garis singgung persekutuan untuk lebih banyak lingkaran, hal ini tidak selalu memungkinkan, meskipun lingkaran-lingkaran tersebut terletak pada bidang yang sama. Namun dalam beberapa kasus, Anda dapat menemukan garis lurus seperti itu.
Contoh dari kehidupan
Garis singgung persekutuan dua lingkaran sering kali terjadi dalam praktik, meskipun hal ini tidak selalu terlihat. Konveyor, sistem blok, sabuk transmisi katrol, tegangan benang pada mesin jahit, dan bahkan rantai sepeda saja - semua ini adalah contoh kehidupan nyata. Jadi, Anda tidak boleh berpikir bahwa masalah geometri hanya tinggal teori: di bidang teknik, fisika, konstruksi, dan banyak bidang lainnya, masalah tersebut dapat diterapkan secara praktis.
Artikel tersebut memberikan penjelasan rinci tentang definisi, makna geometris turunan dengan notasi grafis. Persamaan garis singgung akan diperhatikan beserta contohnya, persamaan garis singgung kurva orde 2 akan dicari.
Definisi 1Sudut kemiringan garis lurus y = k x + b disebut sudut α, diukur dari arah positif sumbu x ke garis lurus y = k x + b dalam arah positif.
Pada gambar, arah x ditunjukkan dengan panah hijau dan busur hijau, dan sudut kemiringan ditunjukkan dengan busur merah. Garis biru mengacu pada garis lurus.
Definisi 2
Kemiringan garis lurus y = k x + b disebut koefisien numerik k.
Koefisien sudut sama dengan garis singgung garis lurus, dengan kata lain k = t g α.
- Sudut kemiringan suatu garis lurus sama dengan 0 hanya jika garis tersebut sejajar terhadap x dan kemiringannya sama dengan nol, karena garis singgung nol sama dengan 0. Artinya bentuk persamaannya adalah y = b.
- Jika sudut kemiringan garis lurus y = k x + b lancip, maka syarat 0 terpenuhi< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение lereng k dianggap bilangan positif, karena nilai tangennya memenuhi syarat t g α > 0, dan terjadi kenaikan grafik.
- Jika α = π 2, maka letak garis tegak lurus x. Kesetaraan ditentukan oleh x = c dengan nilai c adalah bilangan real.
- Jika sudut kemiringan garis lurus y = k x + b tumpul, maka memenuhi syarat π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает arti negatif, dan grafiknya menurun.
Garis potong adalah garis yang melalui 2 titik fungsi f(x). Dengan kata lain, garis potong adalah garis lurus yang ditarik melalui dua titik mana pun pada grafik fungsi yang diberikan.

Gambar tersebut menunjukkan bahwa A B adalah garis potong, dan f (x) adalah kurva hitam, α adalah busur merah yang menunjukkan sudut kemiringan garis potong tersebut.
Jika koefisien sudut suatu garis lurus sama dengan garis singgung sudut kemiringannya, maka jelas bahwa garis singgung segitiga siku-siku A B C dapat dicari dengan perbandingan sisi yang berhadapan dengan sisi yang berdekatan.
Definisi 4
Kami memperoleh rumus untuk mencari garis potong bentuk:
k = t g α = B C A C = f (x B) - f x A x B - x A, dimana absis titik A dan B adalah nilai x A, x B, dan f (x A), f (x B) adalah fungsi nilai pada titik-titik ini.
Jelasnya, koefisien sudut garis potong ditentukan dengan menggunakan persamaan k = f (x B) - f (x A) x B - x A atau k = f (x A) - f (x B) x A - x B , dan persamaannya harus ditulis sebagai y = f (x B) - f (x A) x B - x A x - x A + f (x A) atau
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .
Garis potong membagi grafik secara visual menjadi 3 bagian: di sebelah kiri titik A, dari A ke B, di sebelah kanan B. Gambar di bawah menunjukkan bahwa ada tiga garis potong yang dianggap berhimpitan, yaitu diatur dengan menggunakan a persamaan serupa.

Menurut definisinya, jelas bahwa garis lurus dan garis potongnya dalam hal ini bertepatan.
Garis potong dapat memotong grafik suatu fungsi tertentu beberapa kali. Jika terdapat persamaan berbentuk y = 0 untuk suatu garis potong, maka banyaknya titik potong dengan sinusoidal tersebut tidak terhingga.
Definisi 5
Bersinggungan dengan grafik fungsi f (x) di titik x 0 ; f (x 0) adalah garis lurus yang melalui suatu titik tertentu x 0; f (x 0), dengan adanya ruas yang mempunyai banyak nilai x mendekati x 0.
Contoh 1
Mari kita lihat lebih dekat contoh di bawah ini. Maka jelas bahwa garis yang didefinisikan oleh fungsi y = x + 1 dianggap bersinggungan dengan y = 2 x di titik yang koordinatnya (1; 2). Untuk lebih jelasnya, perlu diperhatikan grafik yang nilainya mendekati (1; 2). Fungsi y = 2 x ditampilkan dalam warna hitam, garis biru adalah garis singgung, dan titik merah adalah titik potongnya.

Jelasnya, y = 2 x menyatu dengan garis y = x + 1.
Untuk menentukan garis singgung, kita harus memperhatikan perilaku garis singgung A B ketika titik B mendekati titik A tanpa batas.Untuk lebih jelasnya, kami sajikan sebuah gambar.

Garis potong A B yang ditunjukkan dengan garis biru cenderung ke posisi garis singgung itu sendiri, dan sudut kemiringan garis potong α akan mulai cenderung ke sudut kemiringan garis singgung itu sendiri α x.
Definisi 6
Garis singgung grafik fungsi y = f (x) di titik A dianggap sebagai posisi pembatas garis potong A B karena B cenderung ke A, yaitu B → A.
Sekarang mari kita beralih ke arti geometri turunan suatu fungsi di suatu titik.
Mari kita lanjutkan dengan mempertimbangkan garis potong A B untuk fungsi f (x), di mana A dan B dengan koordinat x 0, f (x 0) dan x 0 + ∆ x, f (x 0 + ∆ x), dan ∆ x adalah dilambangkan sebagai pertambahan argumen. Sekarang fungsinya akan berbentuk ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Agar lebih jelas, mari kita beri contoh gambarnya.

Perhatikan hasil segitiga siku-siku A B C. Kita menggunakan definisi tangen untuk menyelesaikannya, yaitu kita memperoleh relasi ∆ y ∆ x = t g α . Dari definisi garis singgung dapat disimpulkan bahwa lim ∆ x → 0 ∆ y ∆ x = t g α x . Menurut aturan turunan di suatu titik, kita mendapatkan bahwa turunan f (x) di titik x 0 disebut limit rasio kenaikan fungsi dengan kenaikan argumen, di mana ∆ x → 0 , maka kita nyatakan sebagai f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Oleh karena itu f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, dimana k x dinotasikan sebagai kemiringan garis singgung.
Artinya, kita menemukan bahwa f '(x) dapat ada di titik x 0, dan seperti garis singgung grafik fungsi tertentu di titik singgung sama dengan x 0, f 0 (x 0), di mana nilai kemiringan garis singgung di titik tersebut sama dengan turunan di titik x 0 . Kemudian kita mendapatkan bahwa k x = f " (x 0) .
Arti geometri turunan suatu fungsi di suatu titik adalah memberikan konsep adanya garis singgung grafik di titik yang sama.
Untuk menulis persamaan garis lurus pada suatu bidang, diperlukan koefisien sudut dengan titik yang dilaluinya. Notasinya dianggap x 0 di persimpangan.
Persamaan garis singgung grafik fungsi y = f (x) di titik x 0, f 0 (x 0) berbentuk y = f"(x 0) x - x 0 + f (x 0).
Artinya nilai akhir turunan f"(x 0) dapat menentukan kedudukan garis singgung, yaitu secara vertikal dengan syarat lim x → x 0 + 0 f"(x) = ∞ dan lim x → x 0 - 0 f "(x ) = ∞ atau tidak ada sama sekali dengan syarat lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .
Letak garis singgungnya bergantung pada nilai koefisien sudutnya k x = f" (x 0). Jika sejajar dengan sumbu o x diperoleh k k = 0, jika sejajar dengan o y - k x = ∞, dan bentuk garis singgungnya persamaan tangen x = x 0 bertambah jika k x > 0, berkurang jika k x< 0 .
Contoh 2
Buatlah persamaan garis singgung grafik fungsi y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 di titik dengan koordinat (1; 3) dan tentukan sudut kemiringannya.
Larutan
Dengan syarat kita memiliki fungsi yang didefinisikan untuk semua bilangan real. Diketahui titik yang koordinatnya ditentukan oleh kondisi (1; 3) adalah titik singgung, maka x 0 = - 1, f (x 0) = - 3.
Kita perlu mencari turunannya di titik yang bernilai - 1. Kami mengerti
y" = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Nilai f'(x) pada titik singgung adalah kemiringan garis singgung yang sama dengan kemiringan garis singgung tersebut.
Maka k x = t g α x = y " (x 0) = 3 3
Oleh karena itu α x = a r c t g 3 3 = π 6
Menjawab: persamaan tangen mengambil bentuk
kamu = f " (x 0) x - x 0 + f (x 0) kamu = 3 3 (x + 1) - 3 kamu = 3 3 x - 9 - 3 3
Untuk lebih jelasnya, kami memberikan contoh dalam ilustrasi grafis.
Warna hitam digunakan untuk grafik fungsi asal, warna biru merupakan bayangan garis singgung, dan titik merah merupakan titik singgung. Gambar di sebelah kanan menunjukkan tampilan yang diperbesar.

Contoh 3
Tentukan keberadaan garis singgung grafik suatu fungsi tertentu
y = 3 · x - 1 5 + 1 di titik dengan koordinat (1 ; 1) . Tulis persamaan dan tentukan sudut kemiringannya.
Larutan
Dengan syarat, kita mendapatkan bahwa domain definisi suatu fungsi tertentu dianggap sebagai himpunan semua bilangan real.
Mari kita lanjutkan mencari turunannya
y" = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Jika x 0 = 1, maka f' (x) tidak terdefinisi, tetapi limitnya ditulis sebagai lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ dan lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , artinya adanya garis singgung vertikal di titik (1; 1).
Menjawab: persamaannya akan berbentuk x = 1, dimana sudut kemiringannya sama dengan π 2.
Untuk lebih jelasnya, mari kita gambarkan secara grafis.

Contoh 4
Tentukan titik-titik pada grafik fungsi y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, dimana
- Tidak ada garis singgung;
- Garis singgungnya sejajar dengan x;
- Garis singgungnya sejajar dengan garis y = 8 5 x + 4.
Larutan
Perlu diperhatikan ruang lingkup definisinya. Dengan syarat, kita mendapatkan bahwa fungsi tersebut terdefinisi pada himpunan semua bilangan real. Kami memperluas modul dan menyelesaikan sistem dengan interval x ∈ - ∞ ; 2 dan [ - 2 ; + ∞) . Kami mengerti
y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)
Fungsinya perlu dibedakan. Kami punya itu
kamu" = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)
Jika x = − 2, maka turunannya tidak ada karena batas satu sisinya tidak sama pada titik tersebut:
lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Kita menghitung nilai fungsi di titik x = - 2, dari situ kita mendapatkannya
- y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2 yaitu garis singgung di titik ( - 2; - 2) tidak akan ada.
- Garis singgungnya sejajar dengan x jika kemiringannya nol. Maka k x = t g α x = f "(x 0). Artinya, nilai x tersebut perlu dicari ketika turunan fungsi mengubahnya menjadi nol. Artinya, nilai f ' (x) adalah titik singgung yang garis singgungnya sejajar dengan x .
Ketika x ∈ - ∞ ; - 2, maka - 1 5 (x 2 + 12 x + 35) = 0, dan untuk x ∈ (- 2; + ∞) kita mendapatkan 1 5 (x 2 - 4 x + 3) = 0.
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Hitung nilai fungsi yang sesuai
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Oleh karena itu - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 dianggap sebagai titik-titik yang diperlukan dari grafik fungsi.
Mari kita pertimbangkan gambar grafis solusi.

Garis hitam adalah grafik fungsi, titik merah adalah titik singgungnya.
- Jika garis-garisnya sejajar, koefisien sudutnya sama. Kemudian perlu dicari titik-titik pada grafik fungsi yang kemiringannya sama dengan nilai 8 5. Untuk melakukannya, Anda perlu menyelesaikan persamaan bentuk y "(x) = 8 5. Kemudian, jika x ∈ - ∞; - 2, kita peroleh - 1 5 (x 2 + 12 x + 35) = 8 5, dan jika x ∈ ( - 2 ; + ∞), maka 1 5 (x 2 - 4 x + 3) = 8 5.
Persamaan pertama tidak mempunyai akar karena diskriminannya kurang dari nol. Mari kita tuliskan itu
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Persamaan lain mempunyai dua akar real
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Mari kita lanjutkan mencari nilai fungsinya. Kami mengerti
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Poin dengan nilai - 1; 4 15, 5; 8 3 adalah titik-titik yang garis singgungnya sejajar dengan garis y = 8 5 x + 4.
Menjawab: garis hitam – grafik fungsi, garis merah – grafik y = 8 5 x + 4, garis biru – garis singgung di titik - 1; 4 15, 5; 8 3.

Kemungkinan adanya jumlah yang tak terbatas garis singgung untuk fungsi tertentu.
Contoh 5
Tuliskan persamaan semua garis singgung fungsi y = 3 cos 3 2 x - π 4 - 1 3 yang letaknya tegak lurus terhadap garis lurus y = - 2 x + 1 2.
Larutan
Untuk menyusun persamaan garis singgung perlu dicari koefisien dan koordinat titik singgung berdasarkan syarat tegak lurus garis. Definisinya sebagai berikut: hasil kali koefisien sudut yang tegak lurus garis lurus sama dengan - 1, yaitu ditulis k x · k ⊥ = - 1. Dari syarat diperoleh koefisien sudut terletak tegak lurus garis dan sama dengan k ⊥ = - 2, maka k x = - 1 k ⊥ = - 1 - 2 = 1 2.
Sekarang Anda perlu mencari koordinat titik sentuh. Anda perlu mencari x dan kemudian nilainya untuk fungsi tertentu. Perhatikan dari arti geometri turunan pada suatu titik
x 0 kita peroleh bahwa k x = y"(x 0). Dari persamaan ini kita cari nilai x untuk titik-titik singgungnya.
Kami mengerti
y" (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9
Ini persamaan trigonometri akan digunakan untuk menghitung ordinat titik singgung.
3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk atau 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk atau 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk atau x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z adalah himpunan bilangan bulat.
x titik kontak telah ditemukan. Sekarang Anda perlu melanjutkan mencari nilai y:
kamu 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 atau y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 atau y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 atau y 0 = - 4 5 + 1 3
Dari sini kita peroleh bahwa 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 adalah titik singgungnya.
Menjawab: persamaan yang diperlukan akan ditulis sebagai
y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
Untuk representasi visual, pertimbangkan fungsi dan garis singgung pada garis koordinat.
Gambar tersebut menunjukkan bahwa fungsi tersebut terletak pada interval [ - 10 ; 10 ], dimana garis hitam adalah grafik fungsi, garis biru adalah garis singgung yang terletak tegak lurus terhadap garis tertentu yang berbentuk y = - 2 x + 1 2. Titik merah adalah titik sentuh.

Persamaan kanonik kurva orde ke-2 bukanlah fungsi bernilai tunggal. Persamaan tangen untuk mereka disusun menurut skema yang diketahui.
Bersinggungan dengan lingkaran
Menentukan lingkaran yang berpusat di titik x c e n t e r ; y c e n t e r dan jari-jari R, terapkan rumus x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .
Persamaan ini dapat ditulis sebagai gabungan dua fungsi:
y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r
Fungsi pertama terletak di atas, dan fungsi kedua di bawah, seperti yang ditunjukkan pada gambar.

Untuk menyusun persamaan lingkaran di titik x 0; y 0 , yang terletak pada setengah lingkaran atas atau bawah, carilah persamaan grafik fungsi yang berbentuk y = R 2 - x - x c e n t e r 2 + y c e n t e r atau y = - R 2 - x - x c e n t e r 2 + y c e n t e r pada titik yang ditunjukkan.
Ketika di titik x c e n t e r ; y c e n t e r + R dan x c e n t e r ; garis singgung y c e n t e r - R dapat diberikan dengan persamaan y = y c e n t e r + R dan y = y c e n t e r - R , dan di titik x c e n t e r + R ; y c e n t e r dan
x c e n t e r - R ; y c e n t e r akan sejajar dengan oy, maka diperoleh persamaan berbentuk x = x c e n t e r + R dan x = x c e n t e r - R .

Bersinggungan dengan elips
Jika elips mempunyai pusat di x pusat; y c e nter dengan titik tengah a dan b, maka dapat ditentukan dengan persamaan x - x c e nter 2 a 2 + y - y c e nter 2 b 2 = 1.
Elips dan lingkaran dapat dilambangkan dengan menggabungkan dua fungsi yaitu setengah elips atas dan setengah elips bawah. Lalu kita mendapatkannya
y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Jika garis singgung terletak pada titik sudut elips, maka garis singgung tersebut sejajar terhadap x atau terhadap y. Di bawah ini, untuk lebih jelasnya, perhatikan gambarnya.

Contoh 6
Tuliskan persamaan garis singgung elips x - 3 2 4 + y - 5 2 25 = 1 di titik-titik yang nilai x sama dengan x = 2.
Larutan
Kita perlu mencari titik singgung yang sesuai dengan nilai x = 2. Kita substitusikan ke dalam persamaan elips yang ada dan temukan persamaan tersebut
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Lalu 2 ; 5 3 2 + 5 dan 2; - 5 3 2 + 5 adalah titik singgung setengah elips atas dan bawah.
Mari kita lanjutkan mencari dan menyelesaikan persamaan elips terhadap y. Kami mengerti
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 tahun = 5 ± 5 2 4 - x - 3 2
Jelasnya, setengah elips atas ditentukan menggunakan fungsi bentuk y = 5 + 5 2 4 - x - 3 2, dan setengah elips bawah y = 5 - 5 2 4 - x - 3 2.
Mari kita terapkan algoritma standar untuk membuat persamaan garis singgung grafik fungsi di suatu titik. Mari kita tulis persamaan garis singgung pertama di titik 2; 5 3 2 + 5 akan terlihat seperti
y" = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ kamu = 5 2 3 (x - 2) + 5 3 2 + 5
Kita temukan persamaan garis singgung kedua dengan nilai di titik tersebut
2 ; - 5 3 2 + 5 berbentuk
y" = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + kamu 0 ⇔ kamu = - 5 2 3 (x - 2) - 5 3 2 + 5
Secara grafis, garis singgung ditetapkan sebagai berikut:

Bersinggungan dengan hiperbola
Ketika hiperbola mempunyai pusat di x pusat; y pusat dan simpul x pusat + α ; y c e n t e r dan x c e n t e r - α ; y c e nter , pertidaksamaan x - x c e nter 2 α 2 - y - y c e nter 2 b 2 = 1 terjadi, jika dengan simpul x c e nter ; y c e n t e r + b dan x c e n t e r ; y c e n t e r - b , maka ditentukan menggunakan pertidaksamaan x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Hiperbola dapat direpresentasikan sebagai dua fungsi gabungan dari bentuk tersebut
y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r atau y = ba · (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - ba · (x - x c e n t e r) 2 + a 2 + y c e n t e r

Dalam kasus pertama kita mendapatkan bahwa garis singgungnya sejajar dengan y, dan dalam kasus kedua garis singgungnya sejajar dengan x.
Oleh karena itu, untuk mencari persamaan garis singgung suatu hiperbola, perlu diketahui fungsi titik singgung tersebut. Untuk menentukannya, perlu dilakukan substitusi ke dalam persamaan dan diperiksa identitasnya.
Contoh 7
Tuliskan persamaan garis singgung hiperbola x - 3 2 4 - y + 3 2 9 = 1 di titik 7; - 3 3 - 3 .
Larutan
Catatan solusi untuk mencari hiperbola perlu diubah menggunakan 2 fungsi. Kami mengerti
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 dan y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Penting untuk mengidentifikasi fungsi mana yang dimilikinya set point dengan koordinat 7; - 3 3 - 3 .
Tentunya untuk memeriksa fungsi pertama diperlukan y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, maka titik tersebut tidak termasuk dalam grafik, karena kesetaraan tidak berlaku.
Untuk fungsi kedua kita mendapatkan y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, artinya titik tersebut termasuk dalam grafik yang diberikan. Dari sini Anda akan menemukan kemiringannya.
Kami mengerti
y" = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Menjawab: persamaan tangen dapat direpresentasikan sebagai
kamu = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Digambarkan dengan jelas seperti ini:

Bersinggungan dengan parabola
Untuk membuat persamaan garis singgung parabola y = a x 2 + b x + c di titik x 0, y (x 0), harus menggunakan algoritma standar, maka persamaan tersebut akan berbentuk y = y” (x 0) x - x 0 + y ( x 0). Garis singgung pada titik sudut tersebut sejajar dengan x.
Anda harus mendefinisikan parabola x = a y 2 + b y + c sebagai gabungan dua fungsi. Oleh karena itu, kita perlu menyelesaikan persamaan y. Kami mengerti
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Digambarkan secara grafis sebagai:

Untuk mengetahui apakah suatu titik x 0, y (x 0) termasuk dalam suatu fungsi, lanjutkan secara perlahan sesuai dengan algoritma standar. Garis singgung tersebut akan sejajar dengan oy relatif terhadap parabola.
Contoh 8
Tuliskan persamaan garis singgung grafik x - 2 y 2 - 5 y + 3 jika sudut singgungnya adalah 150°.
Larutan
Kita memulai penyelesaiannya dengan merepresentasikan parabola sebagai dua fungsi. Kami mengerti
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8x - 4
Nilai kemiringan sama dengan nilai turunan di titik x 0 fungsi tersebut dan sama dengan garis singgung sudut kemiringan.
Kita mendapatkan:
k x = y"(x 0) = t g α x = t g 150 ° = - 1 3
Dari sini kita menentukan nilai x untuk titik kontak.
Fungsi pertama akan ditulis sebagai
y" = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Jelasnya, tidak ada akar real, karena kita mendapat nilai negatif. Kami menyimpulkan bahwa tidak ada garis singgung dengan sudut 150° untuk fungsi seperti itu.
Fungsi kedua akan ditulis sebagai
y" = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Kita mengetahui bahwa titik kontaknya adalah 23 4 ; - 5 + 3 4 .
Menjawab: persamaan tangen mengambil bentuk
kamu = - 1 3 x - 23 4 + - 5 + 3 4
Mari kita gambarkan secara grafis seperti ini:

Jika Anda melihat kesalahan pada teks, silakan sorot dan tekan Ctrl+Enter
Garis lurus yang hanya mempunyai satu titik persekutuan dengan lingkaran disebut garis singgung lingkaran, dan titik persekutuannya disebut titik singgung garis dan lingkaran.
Teorema (sifat garis singgung lingkaran)
Garis singgung lingkaran tegak lurus terhadap jari-jari yang ditarik ke titik singgung tersebut.
Diberikan
A – titik kontak
Membuktikan:p OA
Bukti.
Mari kita buktikan dengan kontradiksi.
Misalkan p adalah OA, maka OA condong ke garis lurus p.
Jika dari titik O kita tarik garis tegak lurus OH terhadap garis lurus p, maka panjangnya lebih kecil dari jari-jarinya: OH< ОА=r

Diketahui jarak pusat lingkaran ke garis lurus p (OH) lebih kecil dari jari-jari (r), yang berarti garis lurus p adalah garis potong (yaitu mempunyai dua titik persekutuan dengan lingkaran), yang bertentangan dengan kondisi teorema (p bersinggungan).
Artinya asumsi tersebut salah, sehingga garis lurus p tegak lurus OA.
Teorema (Sifat ruas garis singgung yang ditarik dari satu titik)
Ruas garis singgung lingkaran yang ditarik dari satu titik adalah sama besar dan sama besar sudut yang sama dengan garis lurus yang melalui titik ini dan pusat lingkaran. 
Diberikan: kira-kira. (Atau)
AB dan AC bersinggungan dengan lingkungan. (Atau)
Membuktikan: AB=AC
Bukti
1) OB AB, OS AC, sebagai jari-jari yang ditarik ke titik singgung (sifat tangen)
2) Pertimbangkan tr. AOB, dll. AOS – hal/u
JSC – umum
OB=OS (sebagai jari-jari)
Artinya ABO = AOC (menurut sisi miring dan kaki). Karena itu,
AB = AC,<3 = < 4 (как соответственные элементы в равных тр-ках). ч.т.д.
Teorema (Uji tangensial)
Jika sebuah garis melewati ujung jari-jari yang terletak pada sebuah lingkaran dan tegak lurus terhadap jari-jari tersebut, maka garis tersebut merupakan garis singgung. 
Diberikan: OA – jari-jari lingkaran
Membuktikan: p- bersinggungan dengan lingkaran
Bukti
OA – jari-jari lingkaran (sesuai kondisi) (OA=r)
OA – tegak lurus dari O ke garis lurus p (OA =d)
Artinya r=OA=d yang artinya garis lurus p dan lingkaran mempunyai satu titik persekutuan.
Jadi garis p bersinggungan dengan lingkaran. dll.
3.Sifat akord dan garis potong.
Sifat-sifat garis singgung dan garis potong
DEFINISI
Lingkar adalah tempat kedudukan titik-titik yang berjarak sama dari suatu titik, disebut pusat lingkaran.

Ruas garis yang menghubungkan dua titik pada lingkaran disebut akord(pada gambar ini adalah segmen). Tali busur yang melalui pusat lingkaran disebut tali busur diameter lingkaran.
1. Garis singgungnya tegak lurus terhadap jari-jari yang ditarik ke titik kontak.
2. Ruas garis singgung yang ditarik dari satu titik adalah sama besar.
3. Jika garis singgung dan garis potong ditarik dari suatu titik di luar lingkaran, maka kuadrat panjang garis singgung tersebut sama dengan hasil kali garis potong dan bagian luarnya.