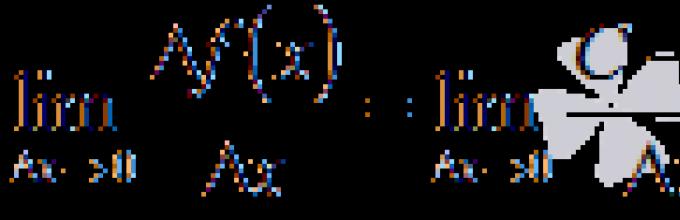Saat menurunkan rumus pertama tabel, kita akan melanjutkan dari definisi turunan fungsi di suatu titik. Ayo bawa kemana X- setiap bilangan real, itu adalah, X– bilangan apa pun dari domain definisi fungsi. Mari kita tuliskan limit rasio pertambahan fungsi terhadap pertambahan argumen di : ![]()
Perlu dicatat bahwa di bawah tanda batas diperoleh ekspresi yang bukan merupakan ketidakpastian nol dibagi nol, karena pembilangnya tidak mengandung nilai yang sangat kecil, melainkan nol. Dengan kata lain, pertambahan fungsi konstanta selalu nol.
Dengan demikian, turunan dari fungsi konstansama dengan nol di seluruh domain definisi.
Turunan dari fungsi pangkat.
Rumus turunan fungsi pangkat mempunyai bentuk ![]() , di mana eksponennya P– bilangan real apa pun.
, di mana eksponennya P– bilangan real apa pun.
Mari kita buktikan dulu rumus eksponen naturalnya, yaitu untuk p = 1, 2, 3, …
Kami akan menggunakan definisi turunan. Mari kita tuliskan limit rasio pertambahan fungsi pangkat dengan pertambahan argumen: 
Untuk menyederhanakan ekspresi pembilangnya, kita beralih ke rumus binomial Newton: 
Karena itu, 
Hal ini membuktikan rumus turunan fungsi pangkat eksponen natural.
Turunan dari fungsi eksponensial.
Kami menyajikan turunan rumus turunan berdasarkan definisi:
Kita telah sampai pada ketidakpastian. Untuk memperluasnya, kami memperkenalkan variabel baru, dan pada . Kemudian . Pada transisi terakhir, kami menggunakan rumus untuk beralih ke basis logaritma baru.
Mari kita substitusikan ke dalam limit aslinya: 
Jika kita mengingat limit luar biasa kedua, kita sampai pada rumus turunan fungsi eksponensial: 
Turunan dari fungsi logaritma.
Mari kita buktikan rumus turunan fungsi logaritma untuk semua X dari domain definisi dan semua nilai basis yang valid A logaritma Berdasarkan definisi turunan kita mempunyai: 
Seperti yang Anda perhatikan, selama pembuktian, transformasi dilakukan menggunakan sifat-sifat logaritma. Persamaan  benar karena batas luar biasa kedua.
benar karena batas luar biasa kedua.
Turunan dari fungsi trigonometri.
Untuk mendapatkan rumus turunan fungsi trigonometri, kita harus mengingat beberapa rumus trigonometri, serta limit pertama yang luar biasa.
Berdasarkan definisi turunan fungsi sinus yang kita miliki ![]() .
.
Mari kita gunakan rumus selisih sinus: 
Masih beralih ke batas luar biasa pertama: 
Jadi, turunan dari fungsi tersebut dosa x Ada karena x.
Rumus turunan kosinus dibuktikan dengan cara yang persis sama. 
Oleh karena itu, turunan dari fungsi tersebut karena x Ada –dosa x.
Kita akan menurunkan rumus tabel turunan tangen dan kotangen menggunakan aturan diferensiasi yang telah terbukti (turunan pecahan). 
Turunan dari fungsi hiperbolik.
Aturan diferensiasi dan rumus turunan fungsi eksponensial dari tabel turunan memungkinkan kita memperoleh rumus turunan sinus hiperbolik, kosinus, tangen, dan kotangen. 
Turunan dari fungsi invers.
Untuk menghindari kebingungan saat presentasi, mari kita nyatakan dalam subskrip argumen fungsi yang digunakan untuk melakukan diferensiasi, yaitu turunan dari fungsi tersebut. f(x) Oleh X.
Sekarang mari kita rumuskan aturan untuk mencari turunan suatu fungsi invers.
Biarkan fungsinya kamu = f(x) Dan x = g(kamu) saling berbanding terbalik, ditentukan pada interval dan masing-masing. Jika pada suatu titik terdapat turunan berhingga dari fungsi tersebut f(x), maka pada titik tersebut terdapat turunan berhingga dari fungsi inversnya g(kamu), Dan ![]() . Di postingan lain
. Di postingan lain ![]() .
.
Aturan ini dapat dirumuskan ulang untuk siapa pun X dari interval , maka kita peroleh  .
.
Mari kita periksa validitas rumus ini.
Mari kita cari fungsi invers logaritma natural ![]() (Di Sini kamu adalah fungsi, dan X- argumen). Setelah menyelesaikan persamaan ini untuk X, kita dapatkan (di sini X adalah fungsi, dan kamu– argumennya). Itu adalah,
(Di Sini kamu adalah fungsi, dan X- argumen). Setelah menyelesaikan persamaan ini untuk X, kita dapatkan (di sini X adalah fungsi, dan kamu– argumennya). Itu adalah, ![]() dan fungsi yang saling invers.
dan fungsi yang saling invers.
Dari tabel turunan kita melihatnya ![]() Dan
Dan ![]() .
.
Mari kita pastikan bahwa rumus untuk mencari turunan fungsi invers memberikan hasil yang sama: 
Pembelajaran dan presentasi dengan topik: "Bilangan e. Fungsi. Grafik. Sifat"
Bahan tambahan
Pengguna yang terhormat, jangan lupa untuk meninggalkan komentar, ulasan, keinginan Anda! Semua materi telah diperiksa oleh program anti-virus.
Alat peraga dan simulator di toko online Integral untuk kelas 11
Manual interaktif untuk kelas 9–11 "Trigonometri"
Manual interaktif untuk kelas 10–11 "Logaritma"
Teman-teman, hari ini kita akan mempelajari nomor khusus. Ia menempati tempat terpisah dalam matematika "dewasa" dan memiliki banyak sifat luar biasa, beberapa di antaranya akan kita bahas.
Mari kita kembali ke fungsi eksponensial $y=a^x$, di mana $a>1$. Kita dapat memplot banyak grafik fungsi berbeda untuk basis berbeda.
Namun perlu diperhatikan bahwa:
- semua fungsi melewati titik (0;1),
- untuk $x→-∞$, grafiknya memiliki asimtot horizontal $y=0$,
- semua fungsi meningkat dan cembung ke bawah,
- dan juga kontinu, yang berarti keduanya dapat terdiferensiasi.
Mari kita pertimbangkan fungsi $y=2^x$ dan buat garis singgung padanya.
Setelah memplot grafik kita dengan cermat, Anda dapat melihat bahwa sudut kemiringan garis singgung adalah 35°.
Sekarang mari kita plot fungsinya $y=3^x$ dan juga plot garis singgungnya: 
Kali ini sudut singgungnya kira-kira 48°. Secara umum, perlu diperhatikan: semakin besar basisnya Fungsi eksponensial, semakin besar sudut kemiringannya.
Yang menarik adalah garis singgung dengan sudut kemiringan sebesar 45°. Pada grafik fungsi eksponensial manakah garis singgung tersebut dapat ditarik di titik (0;1)?
Basis fungsi eksponensial harus lebih besar dari 2 tetapi kurang dari 3, karena sudut singgung yang diperlukan tercapai di antara fungsi $y=2^x$ dan $y=3^x$. Jumlah tersebut ditemukan dan ternyata cukup unik.
Fungsi eksponensial yang garis singgungnya melalui titik (0;1) mempunyai sudut kemiringan sebesar 45° biasanya dilambangkan dengan: $y=e^x$ .
Dasar dari fungsi kami adalah bilangan irasional. Matematikawan telah memperoleh perkiraan nilai bilangan ini $e=2.7182818284590…$.
Dalam mata pelajaran matematika sekolah, biasanya dibulatkan ke persepuluhan terdekat, yaitu $e=2,7$.
Mari kita buat grafik fungsi $y=e^x$ dan garis singgung grafik ini. 
Fungsi kami biasanya disebut eksponensial.
Sifat-sifat fungsi $y=e^x$.
1.$D(f)=(-∞;+∞)$.
2. Tidak genap dan tidak ganjil.
3. Meningkat di seluruh domain definisi.
4. Tidak dibatasi dari atas, dibatasi dari bawah.
5. Nilai terbesar TIDAK, nilai terendah TIDAK.
6. Terus menerus.
7. $E(f)=(0; +∞)$.
8. Cembung ke bawah.
Dalam matematika tingkat tinggi telah dibuktikan bahwa fungsi eksponensial dapat terdiferensiasi di semua tempat, dan turunannya sama dengan fungsi itu sendiri: $(e^x)"=e^x$.
Fungsi kami banyak digunakan di banyak bidang matematika (dalam analisis matematika, teori probabilitas, dalam pemrograman), dan banyak objek nyata yang diasosiasikan dengan bilangan ini.
Contoh.
Tentukan garis singgung grafik fungsi $y=e^x$ di titik $x=2$.
Larutan.
Persamaan tangen digambarkan dengan rumus: $y=f(a)+f"(a)(x-a)$.
Kami secara berurutan menemukan nilai yang diperlukan:
1.$f(a)=f(2)=e^2$.
2.$f"(a)=e^a$.
3.$f"(2)=e^2$.
4. $y=f(a)+f"(a)(x-a)=e^2+e^2(x-2)=e^2*x-e^2$.
Jawaban: $y=e^2*x-e^2$
Contoh.
Tentukan nilai turunan fungsi $y=e^(3x-15)$ di titik $x=5$.
Larutan.
Mari kita ingat aturan untuk membedakan fungsi berbentuk $y=f(kx+m)$.
$y"=k*f"(kx+m)$.
Dalam kasus kita $f(kx+m)=e^(3x-15)$.
Mari kita cari turunannya:
$y"=(e^(3x-15))"=3*e^(3x-15)$.
$y"(5)=3*e^(15-15)=3*e^0=3$.
Jawaban: 3.
Contoh.
Periksa fungsi $y=x^3*e^x$ untuk mengetahui ekstremnya.
Larutan.
Mari kita cari turunan dari fungsi kita $y"=(x^3*e^x)"=(x^3)"*e^x+x^3(e^x)"=3x^2*e^x +x^ 3*e^x=x^2*e^x(x+3)$.
Fungsi tersebut tidak memiliki titik kritis, karena turunannya ada untuk sembarang x.
Menyamakan turunannya dengan 0, kita mendapatkan dua akar: $x_1=0$ dan $x_2=-3$.
Mari kita tandai titik-titik kita pada garis bilangan: 
Masalah untuk diselesaikan secara mandiri
1. Tentukan garis singgung grafik fungsi $y=e^(2x)$ di titik $x=2$.2. Tentukan nilai turunan fungsi $y=e^(4x-36)$ di titik $x=9$.
3. Periksa fungsi $y=x^4*e^(2x)$ untuk mengetahui ekstremnya.
Untuk menggunakan pratinjau presentasi, buat akun Google dan masuk ke akun tersebut: https://accounts.google.com
Keterangan slide:
TURUNAN FUNGSI EKSPONENSIAL Nomor e Kelas 11
PENGULANGAN adalah ibu dari pembelajaran!
Definisi Fungsi Fungsi Eksponensial, diberikan oleh rumus y = a x (di mana a > 0, a ≠ 1) disebut fungsi eksponensial dengan basis a.
Sifat-sifat fungsi eksponensial y = a x a>1 0
Penentuan turunan suatu fungsi di titik x 0. sebagai Δ → 0. Turunan fungsi f di titik x 0 adalah bilangan yang perbandingan selisihnya cenderung sebagai Δx → 0.
Arti geometri turunan x ₀ α A y = f(x) 0 x y к = tan α = f" (x ₀) Koefisien sudut garis singgung grafik fungsi f (x) di titik (x 0 ; f(x 0) sama dengan turunan fungsi f"(x ₀). f(x 0)
Permainan: “Cari pasangannya” (u + v)" cos x e (u v)" n xⁿ ⁻" p (u / v)" - 1 /(sin² x) a (x ⁿ)" - sin x n C "u" v +u v" ke (C u)" 1 / (cos ² x) t (sin x)" (u" v – u v") / v² c (cos x)" 0 o (tg x)" u " + v " e (ctg x) " C u " n
Periksa dirimu sendiri! (u + v)" u" + v" e (u v)" u" v + u v " ke (u /v)" (u' v –u v") / v² s (x ⁿ)" n x ⁿ ⁻¹ p C" 0 o (Cu)" C u " n (sin x)" Cos x e (cos x)" - sin x n (tg x)" 1 / (cos² x) t (ctg x)" - 1 / (sin² x ) A
Eksponennya adalah fungsi daya. Eksponen adalah fungsi yang e adalah basis logaritma natural.
1 y= e x 45° Fungsi y= e x disebut “eksponen” x ₀ =0; tg 45° = 1 Di titik (0;1) kemiringan garis singgung grafik fungsi k = tg 45° = 1 - makna geometris turunan dari eksponen Eksponen y = e x
Teorema 1. Fungsi y = e terdiferensiasi pada setiap titik domain definisi, dan (e)" = e x x x Logaritma natural (ln) adalah logaritma basis e: ln x = log x e Fungsi eksponensial dapat terdiferensialkan pada setiap titik pada domain definisi, dan (a)" = a ∙ ln a x x Teorema 2.
Rumus diferensiasi fungsi eksponensial (e)" = e ; (e)" = k e ; (a)" = a ∙ ln a; (a)" = k a ∙ ln a. x kx + b x x x kx + b kx + b kx + b F(a x) = + C; F(ex) = ex+C.
“Latihan menghasilkan penguasaan.” Tacitus Publius Cornelius - sejarawan Romawi kuno
Contoh: Carilah turunan fungsi: 1. = 3 e. 2. (e)" = (5x)" e = 5 e. 3. (4)" = 4 ln 4. 4. (2)" = (-7 x)" 2 ∙ ln 2 = -7 ∙ 2 ∙ ln 2. 5 x 5 x x (3 e)" 5 x - 7 x x x -7 x -7 x x
Hal-hal menarik di dekatnya
Leonhard Euler 1707 -1783 Ilmuwan Rusia - matematikawan, fisikawan, mekanik, astronom... Memperkenalkan sebutan untuk bilangan e. Membuktikan bahwa bilangan e ≈ 2, 718281... tidak rasional. John Napier 1550 – 1617 Matematikawan Skotlandia, penemu logaritma. Untuk menghormatinya, angka e disebut “bilangan Neper”.
Pertumbuhan dan peluruhan suatu fungsi dengan laju eksponensial disebut eksponensial
Tujuan pelajaran: membentuk gagasan tentang bilangan e; membuktikan diferensiabilitas suatu fungsi pada suatu titik X;perhatikan pembuktian teorema diferensiabilitas suatu fungsi; memeriksa kematangan keterampilan dan kemampuan ketika memecahkan contoh penerapannya.
Tujuan pelajaran.
Edukasi: mengulang kembali pengertian turunan, aturan diferensiasi, turunan fungsi dasar, mengingat grafik dan sifat-sifat fungsi eksponensial, mengembangkan kemampuan mencari turunan fungsi eksponensial, menguji pengetahuan menggunakan tugas tes dan a tes.
Perkembangan: mempromosikan pengembangan perhatian, pengembangan pemikiran logis, intuisi matematika, kemampuan menganalisis, dan menerapkan pengetahuan dalam situasi non-standar.
Pendidikan: menumbuhkan budaya informasi, mengembangkan keterampilan bekerja dalam kelompok dan individu.
Metode pengajaran: verbal, visual, aktif.
Bentuk pelatihan: kolektif, individu, kelompok.
Peralatan : buku teks “Aljabar dan permulaan analisis” (diedit oleh Kolmogorov), semua tugas kelompok B “Segmen tertutup” diedit oleh A.L. Semenova, I.V.Yashchenko, proyektor multimedia.
Langkah-langkah pelajaran:
- Pernyataan topik, maksud dan tujuan pelajaran (2 menit).
- Persiapan mempelajari materi baru dengan mengulang materi yang telah dipelajari sebelumnya (15 menit).
- Pengenalan materi baru (10 menit)
- Pemahaman awal dan konsolidasi pengetahuan baru (15 menit).
- Tugas pekerjaan rumah (1 menit).
- Kesimpulannya (2 menit).
Selama kelas
1. Momen organisasi.
Topik pelajaran diumumkan: “Turunan dari fungsi eksponensial. Nomor e.”, tujuan, sasaran. Geser 1. Presentasi
2. Aktivasi ilmu pendukung.
Untuk melakukan ini, pada tahap pertama pelajaran kita akan menjawab pertanyaan dan memecahkan masalah pengulangan. Geser 2.
Di papan tulis, dua siswa mengerjakan kartu, menyelesaikan tugas seperti B8 Unified State Examination.
Tugas untuk siswa pertama:
Tugas untuk siswa kedua:

Siswa lainnya melakukan pekerjaan mandiri sesuai dengan pilihan berikut:
| Pilihan 1 | pilihan 2 | ||
| 1. |  |
1. |  |
| 2. |  |
2. |  |
| 3. |  |
3. |  |
| 4. |  |
4. |  |
| 5. |  |
5. |  |
Berpasangan bertukar solusi dan mengecek pekerjaan masing-masing, mengecek jawaban pada slide 3.
Keputusan dan jawaban siswa yang bekerja di dewan dipertimbangkan.
Penyelidikan pekerjaan rumah Nomor 1904. Slide 4 ditampilkan.
3. Memperbarui topik pelajaran, menciptakan situasi masalah.
Guru meminta untuk mendefinisikan fungsi eksponensial dan menyebutkan sifat-sifat fungsi y = 2 x. Grafik fungsi eksponensial digambarkan sebagai garis halus yang setiap titiknya dapat ditarik garis singgungnya. Namun keberadaan garis singgung grafik suatu fungsi di suatu titik dengan absis x 0 setara dengan diferensiasinya di x 0.
Untuk grafik fungsi y = 2 x dan y = 3 x, kita tarik garis singgungnya di titik dengan absis 0. Sudut kemiringan garis singgung tersebut terhadap sumbu absis masing-masing kira-kira sama dengan 35° dan 48° . Geser 5.
Kesimpulan: jika basis fungsi eksponensial A bertambah dari 2 menjadi, misalnya 10, maka sudut antara garis singgung grafik fungsi di titik x = 0 dan sumbu x berangsur-angsur bertambah dari 35° menjadi 66,5°. Masuk akal untuk berasumsi bahwa ada alasannya A, yang sudutnya adalah 45
Terbukti ada bilangan yang lebih besar dari 2 dan kurang dari 3. Biasanya dilambangkan dengan huruf e. Dalam matematika ditetapkan bahwa bilangan e– tidak rasional, yaitu mewakili pecahan non-periodik desimal tak terbatas.
e = 2,7182818284590…
Catatan (tidak terlalu serius). Geser 6.
Pada slide 7 berikutnya, potret matematikawan hebat muncul - John Napier, Leonhard Euler dan informasi singkat tentang mereka.
- Perhatikan sifat-sifat fungsi y=e x
- Bukti Teorema 1. Slide 8.
- Bukti Teorema 2. Slide 9.
4. Jeda dinamis atau relaksasi mata.
(Posisi awal - duduk, setiap latihan diulang 3-4 kali):
1. Bersandar ke belakang, tarik napas dalam-dalam, lalu sambil mencondongkan tubuh ke depan, buang napas.
2. Bersandar di kursi, tutup kelopak mata, tutup mata rapat-rapat tanpa membuka kelopak mata.
3. Lengan sepanjang badan, gerakan melingkar bahu maju mundur.
5. Konsolidasi materi yang dipelajari.
5.1 Penyelesaian latihan No.538, No.540, No.544c.
5.2 Penerapan pengetahuan, keterampilan dan kemampuan secara mandiri. Pekerjaan verifikasi dalam bentuk tes. Waktu penyelesaian tugas – 5 menit.
Kriteria evaluasi:
“5” – 3 poin
“4” – 2 poin
"3" - 1 poin
6. Menyimpulkan hasil pekerjaan dalam pembelajaran.
- Cerminan.
- Penilaian.
- Penyerahan tugas tes.
7. Pekerjaan Rumah: ayat 41 (1, 2); Nomor 539 (a,b,d); 540 (c, d), 544 (a, b).
“Segmen Tertutup” No. 1950, 2142.
Grafik fungsi eksponensial adalah garis lengkung mulus tanpa kekusutan, yang dapat ditarik garis singgung pada setiap titik yang dilaluinya. Masuk akal untuk berasumsi bahwa jika suatu garis singgung dapat ditarik, maka fungsinya akan terdiferensiasi pada setiap titik dalam domain definisinya.
Kami akan menampilkannya di beberapa sumbu koordinat beberapa grafik fungsi y = x a, Untuk a = 2; sebuah = 2,3; sebuah = 3; sebuah = 3,4.
Di suatu titik dengan koordinat (0;1). Sudut garis singgung ini masing-masing kira-kira 35, 40, 48 dan 51 derajat. Masuk akal untuk berasumsi bahwa dalam interval 2 hingga 3 terdapat bilangan yang sudut kemiringan garis singgungnya adalah 45 derajat.
Mari kita rumuskan pernyataan ini secara tepat: ada bilangan yang lebih besar dari 2 dan kurang dari 3, dilambangkan dengan huruf e, sehingga fungsi eksponensial y = e x di titik 0 mempunyai turunan sama dengan 1. Yaitu: (e ∆x -1) / ∆x cenderung ke 1 karena ∆x cenderung ke nol.
Nomor ini e tidak rasional dan ditulis sebagai pecahan desimal non-periodik tak hingga:
e = 2,7182818284…
Karena e positif dan bukan nol, maka ada logaritma yang berbasis e. Logaritma ini disebut logaritma natural . Dilambangkan dengan ln(x) = log e (x).
Turunan dari fungsi eksponensial
Teorema: Fungsi e x terdiferensiasi pada setiap titik pada domain definisinya, dan (e x)’ = e x .
Fungsi eksponensial a x terdiferensialkan pada setiap titik domain definisinya, dan (a x)’ = (a x)*ln(a).
Akibat wajar dari teorema ini adalah kenyataan bahwa fungsi eksponensial kontinu di titik mana pun dalam domain definisinya.
Contoh: carilah turunan dari fungsi y = 2 x.
Dengan menggunakan rumus turunan fungsi eksponensial, kita memperoleh:
(2 x)' = (2 x)*ln(2).
Jawaban: (2 x)*ln(2).
Antiturunan dari fungsi eksponensial
Untuk fungsi eksponensial a x yang didefinisikan pada himpunan bilangan real, antiturunannya adalah fungsi (a x)/(ln(a)).
ln(a) adalah suatu konstanta, maka (a x / ln(a))’= (1 / ln(a)) * (a x) * ln(a) = a x untuk sembarang x. Kami telah membuktikan teorema ini.
Mari kita perhatikan contoh mencari antiturunan dari fungsi eksponensial.
Contoh: carilah antiturunan dari fungsi f(x) = 5 x. Mari kita gunakan rumus yang diberikan di atas dan aturan untuk mencari antiturunan. Kita peroleh: F(x) = (5 x) / (ln(5)) +C.