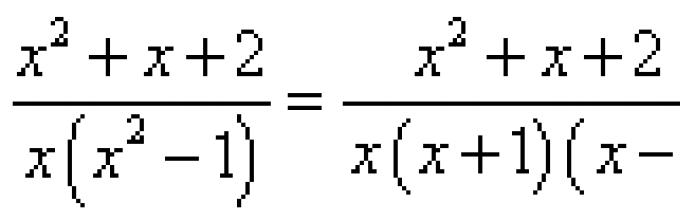Fungsi rasional adalah pecahan yang bentuknya , yang pembilang dan penyebutnya merupakan polinomial atau hasil kali polinomial.

Contoh 1. Langkah 2.

.

Kami mengalikan koefisien yang belum ditentukan dengan polinomial yang tidak termasuk dalam pecahan individu ini, tetapi ada di pecahan lain yang dihasilkan:

Kami membuka tanda kurung dan menyamakan pembilang integral asli dengan ekspresi yang dihasilkan:

Di kedua ruas persamaan, kita mencari suku-suku dengan pangkat x yang sama dan menyusun sistem persamaan dari suku-suku tersebut:

.

Kami membatalkan semua x dan mendapatkan sistem persamaan yang setara:

.

Jadi, perluasan akhir integran menjadi jumlah pecahan sederhana adalah:

.

Contoh 2. Langkah 2. Pada langkah 1, kita memperoleh penguraian pecahan asal berikut menjadi jumlah pecahan sederhana dengan koefisien tak tentu pada pembilangnya:

.

Sekarang kita mulai mencari koefisien tak tentu. Untuk melakukan ini, kita menyamakan pembilang pecahan asli dalam ekspresi fungsi dengan pembilang ekspresi yang diperoleh setelah mengurangi jumlah pecahan menjadi penyebut yang sama:

Sekarang Anda perlu membuat dan menyelesaikan sistem persamaan. Untuk melakukan ini, kita menyamakan koefisien variabel dengan derajat yang sesuai pada pembilang ekspresi asli fungsi dan koefisien serupa dalam ekspresi yang diperoleh pada langkah sebelumnya:

Kami memecahkan sistem yang dihasilkan:

Jadi, dari sini

.

Contoh 3. Langkah 2. Pada langkah 1, kita memperoleh penguraian pecahan asal berikut menjadi jumlah pecahan sederhana dengan koefisien tak tentu pada pembilangnya:

Kami mulai mencari koefisien yang tidak pasti. Untuk melakukan ini, kita menyamakan pembilang pecahan asli dalam ekspresi fungsi dengan pembilang ekspresi yang diperoleh setelah mengurangi jumlah pecahan menjadi penyebut yang sama:

Seperti pada contoh sebelumnya, kami membuat sistem persamaan:

Kami mengurangi x dan mendapatkan sistem persamaan yang setara:

Memecahkan sistem, kami memperoleh nilai koefisien tak tentu berikut:

Kami memperoleh dekomposisi akhir integran menjadi jumlah pecahan sederhana:

.

Contoh 4. Langkah 2. Pada langkah 1, kita memperoleh penguraian pecahan asal berikut menjadi jumlah pecahan sederhana dengan koefisien tak tentu pada pembilangnya:

.

Kita telah mengetahui dari contoh sebelumnya bagaimana menyamakan pembilang pecahan asli dengan ekspresi pada pembilang yang diperoleh setelah menguraikan pecahan menjadi jumlah pecahan sederhana dan membawa jumlah tersebut ke penyebut yang sama. Oleh karena itu, hanya untuk tujuan kontrol, kami menyajikan sistem persamaan yang dihasilkan:

Memecahkan sistem, kami memperoleh nilai koefisien tak tentu berikut:

Kami memperoleh dekomposisi akhir integran menjadi jumlah pecahan sederhana:

Contoh 5. Langkah 2. Pada langkah 1, kita memperoleh penguraian pecahan asal berikut menjadi jumlah pecahan sederhana dengan koefisien tak tentu pada pembilangnya:

.

Kami secara mandiri mengurangi jumlah ini menjadi penyebut yang sama, menyamakan pembilang ekspresi ini dengan pembilang pecahan aslinya. Hasilnya adalah sistem persamaan berikut:

Memecahkan sistem, kami memperoleh nilai koefisien tak tentu berikut:

.

Kami memperoleh dekomposisi akhir integran menjadi jumlah pecahan sederhana:

.

Contoh 6. Langkah 2. Pada langkah 1, kita memperoleh penguraian pecahan asal berikut menjadi jumlah pecahan sederhana dengan koefisien tak tentu pada pembilangnya:

Kami melakukan tindakan yang sama dengan jumlah ini seperti pada contoh sebelumnya. Hasilnya adalah sistem persamaan berikut:

Memecahkan sistem, kami memperoleh nilai koefisien tak tentu berikut:

.

Kami memperoleh dekomposisi akhir integran menjadi jumlah pecahan sederhana:

.

Contoh 7. Langkah 2. Pada langkah 1, kita memperoleh penguraian pecahan asal berikut menjadi jumlah pecahan sederhana dengan koefisien tak tentu pada pembilangnya:

.

Setelah tindakan tertentu, sistem persamaan berikut harus diperoleh dengan jumlah yang dihasilkan:

Memecahkan sistem, kami memperoleh nilai koefisien tak tentu berikut:

Kami memperoleh dekomposisi akhir integran menjadi jumlah pecahan sederhana:

.

Contoh 8. Langkah 2. Pada langkah 1, kita memperoleh penguraian pecahan asal berikut menjadi jumlah pecahan sederhana dengan koefisien tak tentu pada pembilangnya:

.

Mari kita buat beberapa perubahan pada tindakan yang telah dibawa ke otomatisitas untuk mendapatkan sistem persamaan. Ada teknik buatan yang dalam beberapa kasus membantu menghindari perhitungan yang tidak perlu. Membawa jumlah pecahan ke penyebut yang sama, kita memperoleh dan menyamakan pembilang ekspresi ini dengan pembilang pecahan asli, kita peroleh.

Metode ini dapat diterapkan untuk meminimalkan fungsi aljabar logis dari sejumlah variabel.

Mari kita pertimbangkan kasus tiga variabel. Fungsi Boolean di DNF dapat direpresentasikan dalam bentuk semua jenis suku penghubung yang dapat dimasukkan ke dalam DNF:

dimana kО(0,1) adalah koefisien. Caranya adalah dengan memilih koefisien sedemikian rupa sehingga DNF yang dihasilkan minimal.

Jika sekarang kita menetapkan semua kemungkinan nilai variabel dari 000 hingga 111, kita mendapatkan 2 n (2 3 =8) persamaan untuk menentukan koefisien k:

Mengingat himpunan yang fungsinya bernilai nol, tentukan koefisien yang sama dengan 0 dan coret dari persamaan yang ruas kanannya berisi 1. Dari koefisien yang tersisa di setiap persamaan, satu koefisien disamakan dengan satu, yang menentukan konjungsi peringkat terendah. Koefisien yang tersisa sama dengan 0. Jadi, koefisien satuannya k menentukan bentuk minimum yang sesuai.

Contoh. Minimalkan fungsi tertentu

jika nilainya diketahui: ; ; ; ; ; ; ; .

Larutan.

Setelah mencoret koefisien nol kita mendapatkan:

=1;

=1;

=1.

Mari kita samakan dengan satu koefisien yang sesuai dengan konjungsi pangkat terendah dan mengubah empat persamaan terakhir menjadi 1, dan pada persamaan pertama disarankan untuk menyamakan koefisien tersebut dengan 1. Koefisien yang tersisa diatur ke 0.

Menjawab: jenis fungsi yang diperkecil.

Perlu dicatat bahwa metode koefisien tak tentu efektif bila jumlah variabelnya kecil dan tidak melebihi 5-6.

Kubus multidimensi

Mari kita perhatikan representasi grafis suatu fungsi dalam bentuk kubus multidimensi. Setiap puncak N-kubus berdimensi dapat disesuaian dengan penyusun satuannya.

Subset dari simpul yang ditandai adalah pemetaan N-kubus dimensi dari fungsi Boolean dari N variabel di SDNF.

Untuk menampilkan fungsi dari N variabel yang disajikan dalam DNF apa pun, perlu dibuat korespondensi antara miniterm dan elemennya N kubus -dimensi.

Miniterm dengan peringkat (n-1) dapat dianggap sebagai hasil penggabungan dua miniterm N peringkat -th, yaitu

Pada N-kubus berdimensi ini berhubungan dengan penggantian dua simpul yang hanya berbeda nilai koordinatnya x saya, menghubungkan simpul-simpul ini dengan sebuah sisi (suatu sisi dikatakan menutupi simpul-simpul yang bersisian dengannya).

Jadi, jangka waktu mini ( N Urutan -1) sesuai dengan tepi kubus berdimensi n.

Demikian pula korespondensi miniterm ( N-2) wajah urutan N-kubus berdimensi, yang masing-masing mencakup empat simpul (dan empat sisi).

Elemen N-kubus dimensi, dicirikan oleh S pengukuran disebut S-kotak

Jadi simpulnya adalah 0 kubus, sisinya adalah 1 kubus, permukaannya adalah 2 kubus, dan seterusnya.

Ringkasnya, kita dapat mengatakan bahwa miniterm ( n-S) peringkat di DNF untuk fungsi tersebut N variabel yang ditampilkan S-sebuah kubus, masing-masing S-kubus mencakup semua kubus berdimensi lebih rendah yang hanya terhubung ke simpulnya.

Contoh. Pada Gambar. mengingat pemetaannya

Di sini miniterm dan sesuai dengan 1 kubus ( S=3-2=1), dan jangka pendek x 3 ditampilkan menjadi 2 kubus ( S=3-1=2).

Jadi, DNF apa pun dipetakan N kubus -dimensi secara totalitas S-kubus yang menutupi semua simpul yang sesuai dengan unit penyusunnya (0-kubus).

Konstituen. Untuk variabel x 1,x 2,…xn ekspresi disebut penyusun satuan, dan - konstituen nol (berarti salah satu atau).

Konstituen satu (nol) ini berubah menjadi satu (nol) hanya dengan satu himpunan nilai variabel yang bersesuaian, yang diperoleh jika semua variabel diambil sama dengan satu (nol), dan negasinya sama dengan nol (satu).

Misalnya: konstituennya sesuai dengan himpunan (1011), dan konstituennya nol - atur (1001).

Karena SD(K)NF merupakan disjungsi (konjungsi) konstituen satu (nol), maka dapat dikatakan bahwa fungsi Boolean yang diwakilinya F(x 1 ,x 2 ,…,xn) berubah menjadi satu (nol) hanya untuk kumpulan nilai variabel x 1 ,x 2 ,…,xn, sesuai dengan copstitutet ini. Di set lain fungsi ini berubah menjadi 0 (satu).

Pernyataan sebaliknya juga benar, yang menjadi dasarnya cara untuk mewakili apa pun Fungsi Boolean ditentukan oleh tabel.

Untuk melakukan ini, perlu untuk menulis disjungsi (konjungsi) dari konstituen satu (nol), yang sesuai dengan himpunan nilai variabel yang fungsinya mengambil nilai sama dengan satu (nol).

Misalnya fungsi yang diberikan oleh tabel

sesuai

Ekspresi yang dihasilkan dapat diubah ke bentuk lain berdasarkan sifat-sifat aljabar logika.

Pernyataan sebaliknya juga benar: jika ada kumpulan S-kubus mencakup himpunan semua simpul yang bersesuaian dengan nilai satuan fungsi, kemudian disjungsi yang bersesuaian dengan nilai tersebut S-kubus miniterm adalah ekspresi fungsi ini di DNF.

Mereka bilang koleksi seperti itu S-kubus (atau minitermnya yang sesuai) membentuk penutup fungsi. Keinginan akan bentuk minimal secara intuitif dipahami sebagai pencarian penutup, angka S-yang jumlah kubusnya lebih sedikit, dan dimensinya S- lagi. Cakupan yang sesuai dengan bentuk minimum disebut cakupan minimum.

Misalnya saja untuk fungsinya pada= lapisannya sesuai dengan bentuk yang tidak minimal.

Kesetaraan (I) adalah identitas. Jika direduksi menjadi bentuk bilangan bulat, kita memperoleh persamaan 2 polinomial. Namun persamaan tersebut selalu dipenuhi hanya jika persamaan suku demi suku dari polinomial tersebut terpenuhi.

Menyamakan koefisien pangkat x yang sama di ruas kiri dan kanan persamaan, kita memperoleh sistem persamaan linier untuk koefisien yang tidak diketahui yang harus diselesaikan.

Karena pemuaian (I) selalu ada untuk pecahan rasional apa pun, sistem yang dihasilkan selalu konsisten.

Cara mencari koefisien seperti ini disebut metode koefisien tak tentu (suatu metode membandingkan koefisien).

Mari kita beri contoh penguraian fungsi rasional menjadi pecahan dasar.

Contoh 6.6.27. Memecah pecahan menjadi pecahan dasar.

substitusikan persamaan terakhir ke persamaan kedua

Dengan demikian,
.

x=2 ;

x=3 .

Sebaiknya; .

Metode nilai parsial memerlukan lebih sedikit tenaga kerja dan oleh karena itu perlu mendapat perhatian khusus ketika mengintegrasikan pecahan rasional.

Jika akar-akar penyebutnya hanya nyata, maka disarankan menggunakan metode ini untuk menentukan koefisien yang tidak diketahui.

Dalam kasus lain, kedua metode dapat digabungkan untuk menentukan koefisien yang tidak diketahui.

Komentar. Metode nilai parsial juga digunakan dalam kasus lain, namun di sini identitasnya harus dibedakan.

Jadi, untuk mengintegrasikan pecahan rasional yang benar, cukup dengan:

1) mengintegrasikan pecahan dasar;

2) menguraikan pecahan rasional menjadi pecahan dasar.

3. Integrasi pecahan rasional

Skema pengintegrasian pecahan rasional:

Untuk mengintegrasikan pecahan rasional ;

Dimana P(x) dan Q(x) adalah polinomial dengan koefisien real, tiga langkah dilakukan secara berurutan.

Langkah pertama. Jika suatu pecahan tidak wajar, yaitu pangkat pembilang P(x) lebih besar atau sama dengan pangkat penyebut Q(x), pisahkan seluruh bagian pecahan rasional tersebut dengan membagi pembilangnya dengan penyebutnya sesuai dengan aturan membagi polinomial dengan polinomial. Setelah itu, pecahan rasional dapat dituliskan sebagai penjumlahan:

1) bagian bilangan bulat yang dipilih – polinomial M(x);

2) pecahan sisa wajar :

Tahap kedua.

Pecahan sisa wajar diuraikan menjadi pecahan-pecahan berikutnya.

Caranya, cari akar-akar persamaan Q(x)=0 dan dekomposisi penyebut Q(x) menjadi faktor derajat pertama dan kedua dengan koefisien riil:

Dalam perluasan penyebut ini, faktor-faktor derajat 1 berhubungan dengan akar-akar real, dan faktor-faktor derajat 2 berhubungan dengan akar-akar konjugasi paralel.

Koefisien pangkat x yang lebih besar pada penyebut Q(x) dapat dianggap sama dengan 1, karena hal ini selalu dapat dicapai dengan membagi P(x) dan Q(x) dengan koefisien tersebut.

Setelah itu, pecahan sisa yang sebenarnya didekomposisi menjadi pecahan paling sederhana (dasar).

Langkah ketiga. Temukan integral dari bagian bilangan bulat yang dipilih dan semua pecahan dasar (menggunakan metode yang dibahas di atas), yang kemudian dijumlahkan.

Contoh6.6.28.

Di bawah tanda integral ada pecahan rasional tak wajar, karena derajat pembilangnya sama dengan derajat penyebutnya, jadi kita pilih bagian bilangan bulatnya.

KEMENTERIAN PENGETAHUAN DAN PENDIDIKAN REPUBLIK BASHKORTO STAN

SAOU SPO Sekolah Tinggi Arsitektur dan Teknik Sipil Bashkir

Khaliullin Askhat Adelzyanovich,

guru matematika di Bashkirsky

Sekolah Tinggi Arsitektur dan Teknik Sipil

UFA

2014

Pendahuluan ____________________________________________________3

Bab SAYA. Aspek teoritis penggunaan metode koefisien tak tentu_____________________________________________4

Bab II. Mencari penyelesaian masalah polinomial dengan menggunakan metode koefisien tak tentu_________________________________7

2.1.Memfaktorkan polinomial________ 7

2.2. Masalah dengan parameter_________________________________ 10

2.3. Menyelesaikan persamaan______________________________14

2.4. Persamaan fungsional________________19

Kesimpulan_________________________________________________23

Daftar literatur bekas________________24

Aplikasi ________________________________________________25

Perkenalan.

Karya ini dikhususkan untuk aspek teoretis dan praktis dalam memperkenalkan metode koefisien tak tentu ke dalam mata pelajaran matematika sekolah. Relevansi topik ini ditentukan oleh keadaan berikut.

Tidak ada yang akan berpendapat bahwa matematika sebagai ilmu tidak berdiri di satu tempat, ia terus berkembang, muncul tugas-tugas baru dengan kompleksitas yang meningkat, yang seringkali menimbulkan kesulitan tertentu, karena tugas-tugas ini biasanya dikaitkan dengan penelitian. Dalam beberapa tahun terakhir, soal-soal seperti itu telah diusulkan di Olimpiade matematika sekolah, distrik dan republik, dan juga tersedia dalam versi Ujian Negara Bersatu. Oleh karena itu, diperlukan metode khusus yang memungkinkan setidaknya beberapa di antaranya diselesaikan dengan paling cepat, efisien, dan terjangkau. Karya ini dengan jelas menyajikan isi metode koefisien tak tentu, yang banyak digunakan dalam berbagai bidang matematika, mulai dari soal-soal yang termasuk dalam mata kuliah pendidikan umum hingga bagian-bagian yang paling maju. Secara khusus, penerapan metode koefisien tak tentu dalam menyelesaikan masalah dengan parameter, persamaan rasional pecahan dan persamaan fungsional sangat menarik dan efektif; mereka dapat dengan mudah menarik minat siapa pun yang tertarik pada matematika. Tujuan utama dari usulan kerja dan pemilihan masalah adalah untuk memberikan kesempatan yang luas untuk mengasah dan mengembangkan kemampuan menemukan solusi yang singkat dan tidak baku.

Karya ini terdiri dari dua bab. Yang pertama membahas aspek teoritis penggunaan

metode koefisien tidak pasti, dan kedua, aspek praktis dan metodologis dari penggunaan tersebut.

Lampiran pekerjaan memberikan kondisi untuk tugas-tugas khusus untuk solusi independen.

Bab SAYA . Aspek teoritis penggunaan metode koefisien tidak pasti

“Astaga… terlahir untuk menjadi seorang master,

penguasa, raja alam, tetapi kebijaksanaan,

yang dengannya dia harus memerintah tidak diberikan kepadanya

sejak lahir: diperoleh melalui pembelajaran"

N.I.Lobachevsky

Ada berbagai cara dan metode untuk menyelesaikan masalah, tetapi salah satu yang paling nyaman, paling efektif, orisinal, elegan dan sekaligus sangat sederhana dan dapat dimengerti oleh semua orang adalah metode koefisien tak tentu. Metode koefisien tak tentu merupakan suatu metode yang digunakan dalam matematika untuk mencari koefisien-koefisien yang bentuknya telah diketahui sebelumnya.

Sebelum mempertimbangkan penerapan metode koefisien tak tentu untuk menyelesaikan berbagai jenis masalah, kami menyajikan sejumlah informasi teoretis.

Biarkan mereka diberikan

A N (X) = A 0 X N + A 1 X n-1 + A 2 X n-2 + ··· + A n-1 X + A N

B M (X ) = B 0 X M + B 1 X M -1 + B 2 X M -2 + ··· + B m-1 X + B M ,

polinomial relatif X dengan segala rintangan.

Dalil. Dua polinomial bergantung pada satu dan argumen yang sama identik sama jika dan hanya jikaN = M dan koefisiennya adalah samaA 0 = B 0 , A 1 = B 1 , A 2 = B 2 ,··· , A N -1 = B M -1 , A N = B M Dan T. D.

Jelasnya, polinomial yang sama mengambil semua nilai X nilai-nilai yang sama. Sebaliknya jika nilai dua polinomial sama untuk semua nilai X, lalu polinomialnya adalah sama, yaitu koefisiennya pada derajat yang samaX sesuai.

Oleh karena itu, ide penerapan metode koefisien tak tentu dalam penyelesaian masalah adalah sebagai berikut.

Mari kita ketahui bahwa sebagai hasil dari beberapa transformasi, diperoleh ekspresi tipe tertentu dan hanya koefisien dalam ekspresi ini yang tidak diketahui. Kemudian koefisien-koefisien ini dilambangkan dengan huruf dan dianggap tidak diketahui. Sebuah sistem persamaan kemudian dibangun untuk menentukan hal-hal yang tidak diketahui ini.

Misalnya, dalam kasus polinomial, persamaan ini dibuat dengan syarat bahwa koefisiennya sama untuk pangkat yang sama. X untuk dua polinomial yang sama.

Kami akan mendemonstrasikan apa yang dikatakan di atas menggunakan contoh spesifik berikut, dan mari kita mulai dengan yang paling sederhana.

Jadi, misalnya berdasarkan pertimbangan teoritis, pecahan

dapat direpresentasikan sebagai jumlah

, Di mana A , B Dan C - koefisien yang akan ditentukan. Untuk menemukannya, kita menyamakan ekspresi kedua dengan ekspresi pertama:

=

dan membebaskan diri kita dari penyebut dan mengumpulkan suku-suku dengan pangkat yang sama di sebelah kiri X, kita mendapatkan:

(A + B + C )X 2 + ( B - C )x - sebuah = 2X 2 – 5 X– 1

Karena persamaan terakhir harus berlaku untuk semua nilai X, maka koefisien pada pangkat yang samaX kanan dan kiri harus sama. Jadi, diperoleh tiga persamaan untuk menentukan tiga koefisien yang tidak diketahui:

a+b+c = 2

B - C = - 5

A= 1, dari mana A = 1 , B = - 2 , C = 3

Karena itu,

=
,

validitas kesetaraan ini mudah diverifikasi secara langsung.

Misalkan Anda juga perlu merepresentasikan pecahan

sebagai A + B
+ C
+ D
, Di mana A , B , C Dan D- koefisien rasional yang tidak diketahui. Kami menyamakan ekspresi kedua dengan ekspresi pertama:

A + B
+ C
+ D
=
atau, Membebaskan diri dari penyebut, menghilangkan, jika mungkin, faktor-faktor rasional dari bawah tanda-tanda akar dan membawa suku-suku serupa di sisi kiri, kita memperoleh:

(A- 2 B + 3 C ) + (- a+b +3 D )
+ (a+c - 2 D )
+

+ (b - c + D )
= 1 +
-
.

Tetapi persamaan seperti itu hanya mungkin terjadi jika suku-suku rasional kedua bagian dan koefisien dari radikal yang sama adalah sama. Dengan demikian, diperoleh empat persamaan untuk mencari koefisien yang tidak diketahui A , B , C Dan D :

A- 2b+ 3C = 1

- a+b +3 D = 1

a+c - 2 D = - 1

B - C + D= 0, dari mana A = 0 ; B = - ; C = 0 ; D= , yaitu
= -
+
.

Bab II. Mencari solusi untuk masalah polinomial metode koefisien yang tidak ditentukan.

“Tidak ada yang lebih baik dalam memberikan kontribusi pada penguasaan suatu mata pelajaran selain

cara bertindak bersamanya dalam situasi yang berbeda"

Akademisi B.V. Gnedenko

2. 1. Memfaktorkan polinomial.

Metode pemfaktoran polinomial:

1) menempatkan faktor persekutuan di luar tanda kurung, 2) metode pengelompokan; 3) penerapan rumus dasar perkalian; 4) pengenalan suku-suku bantu, 5) transformasi awal suatu polinomial tertentu dengan menggunakan rumus-rumus tertentu; 6) perluasan dengan mencari akar-akar polinomial tertentu; 7) metode memasukkan parameter; 8)metode koefisien yang tidak dapat ditentukan.

Soal 1. Faktorkan polinomial tersebut menjadi faktor riil X 4 + X 2 + 1 .

Larutan. Tidak ada akar di antara pembagi suku bebas polinomial ini. Kita tidak dapat menemukan akar-akar polinomial dengan cara dasar lainnya. Oleh karena itu, tidak mungkin melakukan pemuaian yang diperlukan dengan terlebih dahulu mencari akar-akar polinomial ini. Masih mencari solusi untuk masalah ini baik dengan memperkenalkan suku-suku bantu atau dengan metode koefisien yang tidak dapat ditentukan. Jelas sekali X 4 + X 2 + 1 = X 4 + X 3 + X 2 - X 3 - X 2 - X + X 2 + X + 1 =

= X 2 (X 2 + X + 1) - X (X 2 + X + 1) + X 2 + X + 1 =

= (X 2 + X + 1)(X 2 - X + 1).

Trinomial kuadrat yang dihasilkan tidak mempunyai akar dan oleh karena itu tidak dapat diuraikan menjadi faktor linier nyata.

Metode yang dijelaskan secara teknis sederhana, tetapi sulit karena kepalsuan. Memang, sangat sulit untuk menemukan persyaratan tambahan yang diperlukan. Hanya tebakan yang membantu kami menemukan dekomposisi ini. Tetapi

Ada cara yang lebih dapat diandalkan untuk mengatasi masalah tersebut.

Kita dapat melanjutkan seperti ini: asumsikan bahwa polinomial tertentu terurai menjadi hasil kali

(X 2 + A X + B )(X 2 + C X + D )

dua trinomial persegi dengan koefisien bilangan bulat.

Jadi, kita akan memilikinya

X 4 + X 2 + 1 = (X 2 + A X + B )(X 2 + C X + D )

Masih menentukan koefisiennyaA , B , C Dan D .

Mengalikan polinomial di ruas kanan persamaan terakhir, kita memperoleh:X 4 + X 2 + 1 = X 4 +

+ (a + c ) X 3 + (B + A C + D ) X 2 + (iklan + SM ) x+ bd .

Namun karena kita memerlukan ruas kanan persamaan ini untuk berubah menjadi polinomial yang sama dengan ruas kiri, maka syarat-syarat berikut harus dipenuhi:

a + c = 0

B + A C + D = 1

iklan + SM = 0

bd = 1 .

Hasilnya adalah sistem empat persamaan dengan empat hal yang tidak diketahuiA , B , C Dan D . Koefisien dari sistem ini mudah dicariA = 1 , B = 1 , C = -1 Dan D = 1.

Sekarang masalahnya sudah terpecahkan sepenuhnya. Kita punya:

X 4 + X 2 + 1 = (X 2 + X + 1)(X 2 - X + 1).

Soal 2. Faktorkan polinomial tersebut menjadi faktor riil X 3 – 6 X 2 + 14 X – 15 .

Larutan. Mari kita nyatakan polinomial ini dalam bentuk

X 3 – 6 X 2 + 14 X – 15 = (X + A )(X 2 + bx + C) , Di mana A , B Dan Dengan - koefisien belum ditentukan. Karena dua polinomial identik sama jika dan hanya jika koefisien pangkatnya samaX sama, kemudian menyamakan koefisiennya masing-masingX 2 , X dan suku bebas, kita memperoleh sistem tiga persamaan dengan tiga persamaan yang tidak diketahui:

a+b= - 6

ab + c = 14

ac = - 15 .

Penyelesaian sistem ini akan sangat disederhanakan jika kita memperhitungkan bahwa bilangan 3 (pembagi suku bebas) adalah akar persamaan ini, dan oleh karena itu,A = - 3 ,

B = - 3 Dan Dengan = 5 .

Kemudian X 3 – 6 X 2 + 14 X – 15 = (X – 3)(X 2 – 3 X + 5).

Metode koefisien tak tentu yang diterapkan, dibandingkan dengan metode memasukkan suku-suku bantu di atas, tidak mengandung sesuatu yang dibuat-buat, tetapi memerlukan penerapan banyak prinsip teoretis dan disertai dengan perhitungan yang cukup besar. Untuk polinomial dengan derajat yang lebih tinggi, metode koefisien yang tidak dapat ditentukan ini menyebabkan sistem persamaan yang rumit.

2.2.Tugas dan dengan parameter.

Dalam beberapa tahun terakhir, versi Unified State Examination telah menawarkan tugas dengan parameter. Solusi mereka seringkali menimbulkan kesulitan tertentu. Saat memecahkan masalah dengan parameter, bersama dengan metode lain, Anda dapat menggunakan metode koefisien tak tentu dengan cukup efektif. Metode inilah yang memungkinkan Anda menyederhanakan solusinya dan mendapatkan jawaban dengan cepat.

Tugas 3. Tentukan pada nilai parameter apa A persamaan 2 X 3 – 3 X 2 – 36 X + A – 3 = 0 mempunyai tepat dua akar.

Larutan. 1 cara. Menggunakan turunan.

Mari kita nyatakan persamaan ini dalam bentuk dua fungsi

2x 3 – 3 X 2 – 36 X – 3 = – A .

F (X) = 2x 3 – 3 X 2 – 36 X– 3 dan φ( X ) = – A .

Mari kita jelajahi fungsinyaF (X) = 2x 3 – 3 X 2 – 36 X – 3 menggunakan turunan dan membuat grafiknya secara skematis (Gbr. 1.).

F( – X )F (X ) , F (– X ) – F (X ). Fungsinya tidak genap dan ganjil.

3. Temukan titik kritis dari fungsi tersebut, interval kenaikan dan penurunannya, ekstremnya. F / (X ) = 6 X 2 – 6 X – 36. D (F / ) = R , oleh karena itu kita akan menemukan semua titik kritis dari fungsi tersebut dengan menyelesaikan persamaan F / (X ) = 0 .

6(X 2 – X– 6) = 0 ,

X 2 – X– 6 = 0 ,

X 1 = 3 , X 2 = – 2 dengan teorema kebalikan dari teorema Vieta.

F / (X ) = 6(X – 3)(X + 2).

+ maks - menit +

2 3 X

F / (X) > 0 untuk semua X< – 2 dan X > 3 dan fungsinya kontinu di titik-titikx =– 2 dan X = 3, oleh karena itu, bertambah pada setiap interval (- ; - 2] dan [ 3 ; ).

F / (X ) < 0 pukul - 2 < X< 3, oleh karena itu, berkurang pada interval [- 2; 3 ].

X = - Poin maksimal ke-2, karena pada titik ini tanda turunannya berubah dari"+" hingga "-".

F (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 == 72 – 31 = 41 ,

x = 3 titik minimum, karena pada titik ini tanda turunannya berubah"-" menjadi "+".

F (3) = 2·27 – 3·9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84.

Grafik fungsi φ(X ) = – A adalah garis lurus yang sejajar sumbu x dan melalui suatu titik dengan koordinat (0; – A ). Grafik memiliki dua titik yang sama di –A= 41, yaitu sebuah =– 41 dan – A= – 84, yaitu A = 84 .

pada

41φ( X)

2 3 X

3 F ( X ) = 2x 3 – 3 X 2 – 36 X – 3

Metode 2. Metode koefisien yang tidak dapat ditentukan.

Karena, menurut kondisi soal, persamaan ini hanya boleh mempunyai dua akar, maka persamaannya jelas:

2X 3 – 3 X 2 – 36 X + A – 3 = (x+ B ) 2 (2 X + C ) ,

2X 3 – 3 X 2 – 36 X + A – 3 = 2 X 3 + (4 B + C ) X 2 + (2 B 2 + +2 SM ) X + B 2 C ,

Sekarang menyamakan koefisien pada derajat yang sama X, kita memperoleh sistem persamaan

4 b + c = - 3

2B 2 + 2SM = - 36

B 2 C = A – 3 .

Dari dua persamaan pertama sistem yang kita temukanB 2 + B – 6 = 0, dari mana B 1 = - 3 atau B 2 = 2 . Nilai-nilai yang sesuaiDengan 1 dan Dengan 2 mudah ditemukan dari persamaan pertama sistem:Dengan 1 = 9 atau Dengan 2 = - 11 . Terakhir, nilai parameter yang diinginkan dapat ditentukan dari persamaan terakhir sistem:

A = B 2 C + 3 , A 1 = - 41 atau A 2 = 84.

Jawaban: persamaan ini mempunyai dua persamaan yang berbeda

akar di A= - 41 dan A= 84 .

Tugas 4. Temukan nilai parameter terbesarA , yang persamaannyaX 3 + 5 X 2 + Oh + B = 0

dengan koefisien bilangan bulat mempunyai tiga akar yang berbeda, salah satunya sama dengan – 2.

Larutan. 1 cara. Mengganti X= - 2 di ruas kiri persamaan, kita peroleh

8 + 20 – 2 A + B= 0, yang artinya B = 2 A – 12 .

Karena bilangan - 2 adalah akar, kita dapat mengambil faktor persekutuannya X + 2:

X 3 + 5 X 2 + Oh + B = X 3 + 2 X 2 + 3 X 2 + Oh + (2 A – 12) =

= X 2 (X + 2) + 3 X (X + 2) – 6 X + Oh + (2 A – 12) =

= X 2 (X + 2) + 3 X (X + 2) + (A – 6)(X +2) - 2(A – 6)+ (2 A - 12) =

= (X + 2)(X 2 + 3 X + (A – 6) ) .

Dengan syarat, ada dua akar persamaan lagi. Artinya diskriminan faktor kedua adalah positif.

D =3 2 - 4 (A – 6) = 33 – 4 A > 0, yaitu A < 8,25 .

Tampaknya jawabannya adalah sebuah = 8. Namun jika kita substitusikan angka 8 ke persamaan awal, kita peroleh:

X 3 + 5 X 2 + Oh + B = X 3 + 5 X 2 + 8 X + 4 = (X + 2)(X 2 + 3 X + 2 ) =

= (X + 1) (X + 2) 2 ,

artinya, persamaan tersebut hanya mempunyai dua akar yang berbeda. Tapi ketika sebuah = 7 sebenarnya menghasilkan tiga akar yang berbeda.

Metode 2. Metode koefisien yang tidak dapat ditentukan.

Jika persamaannya X 3 + 5 X 2 + Oh + B = 0 mempunyai akar X = - 2, maka Anda selalu dapat mengambil nomornyaC Dan D sehingga di depan semua orangX kesetaraan itu benar

X 3 + 5 X 2 + Oh + B = (X + 2)(X 2 + Dengan X + D ).

Untuk menemukan angkaC Dan D Mari kita buka tanda kurung di sisi kanan, tambahkan suku serupa dan dapatkan

X 3 + 5 X 2 + Oh + B = X 3 + (2 + Dengan ) X 2 +(2 s + D ) X + 2 D

Menyamakan koefisien pada pangkat yang bersesuaian X kami memiliki sistem

2 + Dengan = 5

2 Dengan + D = A

2 D = B , Di mana c = 3 .

Karena itu, X 2 + 3 X + D = 0 , D = 9 – 4 D > 0 atau

D < 2.25, jadi D (- ; 2 ].

Kondisi masalah dipenuhi oleh nilai D = 1 . Nilai akhir parameter yang diinginkanA = 7.

JAWABAN: kapan sebuah = 7 persamaan ini mempunyai tiga akar yang berbeda.

2.3. Memecahkan persamaan.

“Ingatlah bahwa dengan memecahkan masalah kecil Anda

persiapkan diri Anda untuk menghadapi hal besar dan sulit

tugas baru.”

Akademisi S.L. Sobolev

Saat menyelesaikan beberapa persamaan, Anda dapat dan harus menunjukkan akal dan kecerdasan, serta menggunakan teknik khusus. Penguasaan berbagai teknik transformasi dan kemampuan melakukan penalaran logis sangat penting dalam matematika. Salah satu triknya adalah dengan menambah dan mengurangi beberapa ekspresi atau angka yang dipilih dengan baik. Fakta yang dinyatakan itu sendiri, tentu saja, diketahui semua orang - kesulitan utamanya adalah melihat dalam konfigurasi tertentu transformasi persamaan yang nyaman dan bijaksana untuk diterapkan.

Dengan menggunakan persamaan aljabar sederhana, kami akan mengilustrasikan salah satu teknik non-standar untuk menyelesaikan persamaan.

Soal 5. Selesaikan persamaannya

=
.

Larutan. Mari kalikan kedua ruas persamaan ini dengan 5 dan tulis ulang sebagai berikut

= 0 ; X 0; -
;

= 0 ,

= 0 ,

= 0 atau
= 0

Mari kita selesaikan persamaan yang dihasilkan dengan menggunakan metode koefisien tak tentu

X 4 - X 3 –7 X – 3 = (X 2 + ah + B )(X 2 + cx + D ) = 0

X 4 - X 3 –7 X – 3 = X 4 + (a + c ) X 3 + (B + A C + D ) X 2 + (iklan + SM ) x+ + bd

Menyamakan koefisien pada X 3 , X 2 , X dan syaratnya gratis, kita dapat sistemnya

a + c = -1

B + A C + D = 0

iklan + SM = -7

bd = -3, dari situ kita temukan:A = -2 ; B = - 1 ;

Dengan = 1 ; D = 3 .

Jadi X 4 - X 3 –7X– 3 = (X 2 – 2 X – 1)(X 2 + X + 3) = 0 ,

X 2 – 2 X– 1 = 0 atau X 2 + X + 3 = 0

X 1,2 =
tidak ada akar.

Demikian pula yang kita miliki

X 4 – 12X – 5 = (X 2 – 2 X – 1)(X 2 + 2X + 5) = 0 ,

Di mana X 2 + 2 X + 5 = 0 , D = - 16 < 0 , нет корней.

Menjawab: X 1,2 =

Soal 6. Selesaikan persamaannya

= 10.

Larutan. Untuk menyelesaikan persamaan ini Anda perlu memilih angkaA Dan B agar pembilang kedua pecahan sama. Oleh karena itu, kami memiliki sistem:

= 0 , X 0; -1 ; -

= - 10

Jadi tugasnya adalah menemukan angka-angkanyaA Dan B , yang menjadi landasan kesetaraan

(sebuah + 6) X 2 + ah - 5 = X 2 + (5 + 2 B ) X + B

Sekarang, menurut teorema persamaan polinomial, ruas kanan persamaan ini harus diubah menjadi polinomial yang sama dengan ruas kiri.

Dengan kata lain, hubungan harus dipenuhi

sebuah + 6 = 1

A = 5 + 2 B

– 5 = B , dari mana kita menemukan nilainyaA = - 5 ;

B = - 5 .

Pada nilai-nilai iniA Dan B persamaan A + B = - 10 juga adil.

= 0 , X 0; -1 ; -

= 0 ,

= 0 ,

(X 2 – 5X– 5)(X 2 + 3X + 1) = 0 ,

X 2 – 5X– 5 = 0 atau X 2 + 3X + 1 = 0 ,

X 1,2 =
, X 3,4 =

Menjawab: X 1,2 =
, X 3,4 =

Soal 7. Selesaikan persamaannya

= 4

Larutan. Persamaan ini lebih kompleks dari persamaan sebelumnya dan oleh karena itu kami akan mengelompokkannya sebagai berikut: X 0;-1;3;-8;12

0 ,

= - 4.

Dari kondisi persamaan dua polinomial

Oh 2 + (sebuah + 6) X + 12 = X 2 + (B + 11) X – 3 B ,

kita memperoleh dan menyelesaikan sistem persamaan untuk koefisien yang tidak diketahuiA Dan B :

A = 1

sebuah + 6 = B + 11

12 = – 3 B , Di mana sebuah = 1 , B = - 4 .

Polinomial - 3 – 6X + cx 2 + 8 cx Dan X 2 + 21 + 12 D – dx sama satu sama lain secara identik hanya jika

Dengan = 1

8 Dengan - 6 = - D

3 = 21 + 12 D , Dengan = 1 , D = - 2 .

Dengan nilai-nilaisebuah = 1 , B = - 4 , Dengan = 1 , D = - 2

persamaan
= - 4 benar.

Hasilnya, persamaan ini mengambil bentuk berikut:

= 0 atau
= 0 atau
= 0 ,

= - 4 , = - 3 , = 1 , = -
.

Dari contoh-contoh yang dipertimbangkan, jelas betapa terampilnya penggunaan metode koefisien tak tentu,

membantu menyederhanakan solusi persamaan yang agak rumit dan tidak biasa.

2.4. Persamaan fungsional.

“Tujuan tertinggi matematika… adalah

adalah menemukan tatanan tersembunyi di dalamnya

kekacauan yang mengelilingi kita"

N.Viner

Persamaan fungsional adalah golongan persamaan yang sangat umum dimana fungsi yang tidak diketahui merupakan fungsi tertentu. Persamaan fungsional dalam arti sempit dipahami sebagai persamaan yang fungsi-fungsi yang diinginkan dihubungkan dengan fungsi-fungsi yang diketahui dari satu atau lebih variabel dengan menggunakan operasi pembentukan fungsi kompleks. Persamaan fungsional juga dapat dianggap sebagai ekspresi properti yang mengkarakterisasi kelas fungsi tertentu

[misalnya, persamaan fungsional F ( X ) = F (- X ) mencirikan kelas fungsi genap, persamaan fungsionalF (X + 1) = F (X ) – kelas fungsi yang memiliki periode 1, dst.].

Salah satu persamaan fungsional yang paling sederhana adalah persamaanF (X + kamu ) = F (X ) + F (kamu ). Solusi kontinu persamaan fungsional ini berbentuk

F (X ) = CX . Namun, pada kelas fungsi diskontinu, persamaan fungsional ini mempunyai solusi lain. Terkait dengan persamaan fungsional yang dipertimbangkan adalah

F (X + kamu ) = F (X ) · F (kamu ), F (X kamu ) = F (X ) + F (kamu ), F (X kamu ) = F (X )· F (kamu ),

solusi kontinu, yang masing-masing memiliki bentuk

e cx , DENGANdalamX , X α (X > 0).

Dengan demikian, persamaan fungsional ini dapat digunakan untuk mendefinisikan fungsi eksponensial, logaritmik, dan pangkat.

Persamaan yang paling banyak digunakan adalah persamaan fungsi kompleks dimana fungsi yang diperlukan adalah fungsi eksternal. Aplikasi teoritis dan praktis

Persamaan inilah yang mendorong para ahli matematika terkemuka untuk mempelajarinya.

Misalnya, pada penyelarasan

F 2 (X) = F (X - kamu)· F (X + kamu)

N.I.Lobachevskydigunakan saat menentukan sudut paralelisme dalam geometri saya.

Dalam beberapa tahun terakhir, permasalahan yang berkaitan dengan penyelesaian persamaan fungsional cukup sering ditawarkan pada olimpiade matematika. Solusi mereka tidak memerlukan pengetahuan di luar cakupan kurikulum matematika di sekolah menengah. Namun, penyelesaian persamaan fungsional seringkali menimbulkan kesulitan tertentu.

Salah satu cara untuk mencari solusi persamaan fungsional adalah dengan metode koefisien tak tentu. Dapat digunakan bila bentuk umum fungsi yang diinginkan dapat ditentukan melalui kemunculan persamaan. Hal ini berlaku, pertama-tama, pada kasus-kasus ketika solusi persamaan harus dicari di antara fungsi rasional bilangan bulat atau pecahan.

Mari kita uraikan inti dari teknik ini dengan memecahkan masalah berikut.

Tugas 8. FungsiF (X ) didefinisikan untuk semua x nyata dan memenuhi semuaX R kondisi

3 F(X) - 2 F(1- X) = X 2 .

MenemukanF (X ).

Larutan. Karena di sisi kiri persamaan ini di atas variabel bebas x dan nilai fungsinyaF Hanya operasi linier yang dilakukan, dan ruas kanan persamaan adalah fungsi kuadrat, maka wajar jika diasumsikan bahwa fungsi yang diinginkan juga kuadrat:

F (X) = kapak 2 + bx + C , Di manaA, B, C – koefisien yang harus ditentukan, yaitu koefisien tidak pasti.

Mengganti fungsi tersebut ke dalam persamaan, kita sampai pada identitas:

3(kapak 2 + bx+ c) – 2(A(1 – X) 2 + B(1 – X) + C) = X 2 .

kapak 2 + (5 B + 4 A) X + (C – 2 A – 2 B) = X 2 .

Dua polinomial akan sama persis jika keduanya sama

koefisien untuk pangkat yang sama dari variabel:

A = 1

5B + 4A = 0

C– 2 A – 2 B = 0.

Dari sistem ini kita mencari koefisiennya

A = 1 , B = - , C = , Jugamemuaskanpersamaan

3 F (X ) - 2 F (1- X ) = X 2 pada himpunan semua bilangan real. Pada saat yang sama, ada juga yang seperti ituX 0 Tugas 9. Fungsikamu =F(X) untuk semua x terdefinisi, kontinu dan memenuhi kondisiF (F (X)) – F(X) = 1 + 2 X . Temukan dua fungsi tersebut.

Larutan. Dua tindakan dilakukan pada fungsi yang diinginkan - operasi pembuatan fungsi kompleks dan

pengurangan. Mengingat ruas kanan persamaan merupakan fungsi linier, wajar jika kita berasumsi bahwa fungsi yang diinginkan juga linier:F(X) = ah +B , Di manaA DanB – koefisien tidak pasti. Mengganti fungsi ini menjadiF (F ( (X ) = - X - 1 ;

F 2 (X ) = 2 X+ , yang merupakan solusi persamaan fungsionalF (F (X)) – F(X) = 1 + 2 X .

Kesimpulan.

Sebagai kesimpulan, perlu dicatat bahwa karya ini tentunya akan memberikan kontribusi pada studi lebih lanjut tentang metode yang orisinal dan efektif untuk memecahkan berbagai masalah matematika, yang merupakan masalah dengan tingkat kesulitan yang meningkat dan memerlukan pengetahuan yang mendalam tentang kursus matematika sekolah dan logika yang tinggi. budaya Siapapun yang ingin memperdalam ilmu matematika secara mandiri juga akan menemukan Karya ini berisi bahan refleksi dan tugas-tugas menarik yang penyelesaiannya akan membawa manfaat dan kepuasan.

Karya tersebut, dalam kerangka kurikulum sekolah yang ada dan dalam bentuk yang dapat diakses untuk persepsi yang efektif, menguraikan metode koefisien tak tentu, yang membantu memperdalam kursus sekolah dalam matematika.

Tentu saja, semua kemungkinan metode koefisien tak tentu tidak dapat didemonstrasikan dalam satu karya. Faktanya, metode tersebut masih memerlukan kajian dan penelitian lebih lanjut.

Daftar literatur bekas.

Glazer G.I..Sejarah matematika di sekolah.-M.: Pendidikan, 1983.

Gomonov S.A. Persamaan fungsional dalam mata pelajaran matematika sekolah // Matematika di sekolah. – 2000. –№10 .

Dorofeev G.V., Potapov M.K., Rozov N.H.. Panduan matematika - M.: Nauka, 1972.

Kurosh A.G. Persamaan aljabar derajat sembarang - M.: Nauka, 1983.

Likhtarnikov L.M.. Pengenalan dasar persamaan fungsional. – Sankt Peterburg. : Lan, 1997.

Manturov O.V., Solntsev Yu.K., Sorokin Yu.I., Fedin N.G.. Kamus penjelasan istilah matematika.-M.: Education, 1971

Modenov V.P.. Panduan matematika. Bagian 1.-M.: Universitas Negeri Moskow, 1977.

Modenov V.P.. Masalah dengan parameter - M.: Ujian, 2006.

Potapov M.K., Aleksandrov V.V., Pasichenko P.I.. Aljabar dan analisis fungsi dasar - M.: Nauka, 1980.

Khaliullin A.A.. Kamu bisa menyelesaikannya dengan lebih mudah // Matematika di sekolah. – 2003 . - №8 .

Khaliullin.

4. Perluas polinomial 2X 4 – 5X 3 + 9X 2 – 5X+ 3 untuk pengali dengan koefisien bilangan bulat.

5. Berapa nilainya A X 3 + 6X 2 + Oh+ 12 per X+ 4 ?

6. Berapa nilai parameternyaA persamaannyaX 3 +5 X 2 + + Oh + B = 0 dengan koefisien bilangan bulat mempunyai dua akar yang berbeda, salah satunya adalah 1 ?

7. Di antara akar-akar polinomial X 4 + X 3 – 18X 2 + Oh + B dengan koefisien bilangan bulat ada tiga bilangan bulat yang sama. Temukan nilainya B .

8. Temukan nilai integer terbesar dari parameter tersebut A, di mana persamaannya X 3 – 8X 2 + ah +B = 0 dengan koefisien bilangan bulat mempunyai tiga akar yang berbeda, salah satunya sama dengan 2.

9. Pada nilai apa A Dan B pembagian dilakukan tanpa sisa X 4 + 3X 3 – 2X 2 + Oh + B pada X 2 – 3X + 2 ?

10. Polinomial faktor:

A)X 4 + 2 X 2 – X + 2 V)X 4 – 4X 3 +9X 2 –8X + 5 D)X 4 + 12X – 5

B)X 4 + 3X 2 + 2X + 3 G)X 4 – 3X –2 e)X 4 – 7X 2 + 1 .

11. Selesaikan persamaan:

A)
= 2 = 2 F (1 – X ) = X 2 .

Menemukan F (X) .

13. Fungsi pada= F (X) di depan semua orang X didefinisikan, berkesinambungan dan memenuhi kondisi F ( F (X)) = F (X) + X. Temukan dua fungsi tersebut.

Integrasi fungsi rasional pecahan.
Metode koefisien tak tentu

Kami terus berupaya mengintegrasikan pecahan. Kita telah membahas integral beberapa jenis pecahan dalam pelajaran ini, dan pelajaran ini, dalam arti tertentu, dapat dianggap sebagai kelanjutan. Untuk berhasil memahami materi diperlukan keterampilan dasar integrasi, jadi jika Anda baru mulai mempelajari integral, yaitu Anda seorang pemula, maka Anda harus memulai dengan artikel Integral tak tentu. Contoh solusi.

Anehnya, sekarang kita tidak akan banyak membahas tentang mencari integral, melainkan... dalam memecahkan sistem persamaan linear. Dalam kasus ini sangat Saya merekomendasikan untuk mengikuti pelajaran ini, yaitu Anda harus menguasai metode substitusi (metode “sekolah” dan metode penjumlahan (pengurangan) suku demi suku dalam sistem persamaan).

Apa yang dimaksud dengan fungsi rasional pecahan? Secara sederhana, fungsi rasional pecahan adalah pecahan yang pembilang dan penyebutnya mengandung polinomial atau hasil kali polinomial. Apalagi pecahannya lebih canggih dari yang dibahas di artikel Mengintegrasikan Beberapa Pecahan.

Mengintegrasikan Fungsi Pecahan-Rasional yang Tepat

Langsung saja contoh dan algoritma tipikal untuk menyelesaikan integral fungsi rasional pecahan.

Contoh 1

Langkah 1. Hal pertama yang SELALU kita lakukan ketika menyelesaikan integral fungsi rasional pecahan adalah memperjelas pertanyaan berikut: apakah pecahannya benar? Langkah ini dilakukan secara lisan, dan sekarang saya akan menjelaskan caranya:

Pertama kita melihat pembilangnya dan mencari tahu gelar senior polinomial:

Pangkat utama pembilangnya adalah dua.

Sekarang kita melihat penyebutnya dan mencari tahu gelar senior penyebut. Cara yang jelas adalah dengan membuka tanda kurung dan memasukkan istilah serupa, tetapi Anda dapat melakukannya dengan lebih sederhana setiap temukan derajat tertinggi dalam tanda kurung

dan kalikan secara mental: - jadi, pangkat tertinggi penyebutnya sama dengan tiga. Jelas sekali kalau kita buka tanda kurungnya, kita tidak akan mendapat derajat lebih dari tiga.

Kesimpulan: Pembilang derajat mayor DENGAN KETAT lebih kecil dari pangkat tertinggi penyebutnya, yang berarti pecahan tersebut layak.

Jika dalam contoh ini pembilangnya berisi polinomial 3, 4, 5, dst. derajat, maka pecahannya adalah salah.

Sekarang kita hanya akan mempertimbangkan fungsi rasional pecahan biasa. Kasus pangkat pembilangnya lebih besar atau sama dengan pangkat penyebutnya akan dibahas di akhir pelajaran.

Langkah 2. Mari kita faktorkan penyebutnya. Mari kita lihat penyebut kita:

Secara umum, ini sudah merupakan produk dari berbagai faktor, namun tetap saja kita bertanya pada diri sendiri: apakah mungkin untuk mengembangkan sesuatu yang lain? Objek penyiksaan tidak diragukan lagi adalah trinomial persegi. Memecahkan persamaan kuadrat:

Diskriminannya lebih besar dari nol, artinya trinomial tersebut benar-benar dapat difaktorkan:

Aturan umumnya: SEMUA yang ada dalam penyebut BISA difaktorkan – difaktorkan

Mari kita mulai merumuskan solusinya:

Langkah 3. Dengan menggunakan metode koefisien tak tentu, kami memperluas integran menjadi jumlah pecahan sederhana (dasar). Sekarang semuanya akan menjadi lebih jelas.

Mari kita lihat fungsi integran kita:

Dan, tahukah Anda, entah bagaimana sebuah pemikiran intuitif muncul bahwa alangkah baiknya mengubah pecahan besar kita menjadi beberapa pecahan kecil. Misalnya seperti ini:

Timbul pertanyaan, apakah hal ini mungkin dilakukan? Mari kita bernapas lega, teorema analisis matematis yang sesuai menyatakan – ITU MUNGKIN. Dekomposisi seperti itu ada dan unik.

Hanya ada satu tangkapan, kemungkinannya besar Selamat tinggal Kita tidak tahu, oleh karena itu dinamakan metode koefisien tak tentu.

Seperti yang sudah kalian duga, gerakan tubuh selanjutnya memang seperti itu, jangan berkotek! akan ditujukan hanya untuk MENGAKUI mereka - untuk mengetahui kesetaraan mereka.

Hati-hati, saya akan menjelaskan secara detail hanya sekali!

Jadi, mari kita mulai menari dari:

Di sisi kiri kami mengurangi ekspresi menjadi penyebut yang sama:

Sekarang kita dapat dengan aman menghilangkan penyebutnya (karena keduanya sama):

Di sisi kiri kami membuka tanda kurung, tetapi jangan sentuh koefisien yang tidak diketahui untuk saat ini:

Pada saat yang sama, kami mengulangi peraturan sekolah untuk mengalikan polinomial. Ketika saya masih seorang guru, saya belajar mengucapkan aturan ini dengan wajah datar: Untuk mengalikan polinomial dengan polinomial, Anda perlu mengalikan setiap suku dari satu polinomial dengan setiap suku dari polinomial lainnya.

Dari sudut pandang penjelasan yang jelas, lebih baik menempatkan koefisien dalam tanda kurung (walaupun saya pribadi tidak pernah melakukan ini untuk menghemat waktu):

Kami menyusun sistem persamaan linear.
Pertama kita mencari gelar senior:

Dan kami menulis koefisien yang sesuai ke dalam persamaan pertama sistem:

Ingatlah poin berikut ini dengan baik. Apa yang akan terjadi jika tidak ada huruf s di sisi kanan sama sekali? Katakanlah, apakah itu hanya akan dipamerkan tanpa ada persegi? Dalam hal ini, dalam persamaan sistem perlu diberi angka nol di sebelah kanan: . Mengapa nol? Namun karena di ruas kanan Anda selalu dapat menetapkan kuadrat yang sama dengan nol: Jika di ruas kanan tidak ada variabel dan/atau suku bebas, maka kita letakkan nol di ruas kanan persamaan sistem yang bersesuaian.

Kami menulis koefisien yang sesuai ke dalam persamaan kedua sistem:

Dan yang terakhir, air mineral, kami pilih member gratis.

Eh...Aku agak bercanda. Terlepas dari leluconnya - matematika adalah ilmu yang serius. Di kelompok institut kami, tidak ada seorang pun yang tertawa ketika asisten profesor mengatakan bahwa dia akan menyebarkan suku-suku di sepanjang garis bilangan dan memilih yang terbesar. Mari kita serius. Meskipun... siapapun yang masih hidup untuk melihat akhir dari pelajaran ini akan tetap tersenyum dengan tenang.

Sistem sudah siap:

Kami memecahkan sistem:

(1) Dari persamaan pertama kita nyatakan dan substitusikan ke persamaan ke-2 dan ke-3 sistem. Sebenarnya, dimungkinkan untuk menyatakan (atau huruf lain) dari persamaan lain, tetapi dalam hal ini lebih menguntungkan untuk menyatakannya dari persamaan pertama, karena ada peluang terkecil.

(2) Kami menyajikan istilah serupa dalam persamaan ke-2 dan ke-3.

(3) Kita menjumlahkan persamaan ke-2 dan ke-3 suku demi suku, memperoleh persamaan , yang darinya berikut ini

(4) Kita substitusikan ke persamaan kedua (atau ketiga), dari situ kita temukan persamaan tersebut

(5) Substitusikan dan ke dalam persamaan pertama, peroleh .

Jika Anda mengalami kesulitan dengan metode penyelesaian sistem, praktikkanlah di kelas. Bagaimana cara menyelesaikan sistem persamaan linear?

Setelah menyelesaikan sistem, selalu berguna untuk memeriksa - mengganti nilai yang ditemukan setiap persamaan sistem, akibatnya semuanya harus “konvergen”.

Hampir sampai. Koefisien ditemukan, dan:

Pekerjaan yang sudah selesai akan terlihat seperti ini:

Seperti yang Anda lihat, kesulitan utama dari tugas ini adalah menyusun (dengan benar!) dan menyelesaikan (dengan benar!) sistem persamaan linier. Dan pada tahap akhir, semuanya tidak begitu sulit: kita menggunakan sifat linearitas integral tak tentu dan mengintegrasikannya. Harap dicatat bahwa di bawah masing-masing dari tiga integral kita memiliki fungsi kompleks "bebas"; saya berbicara tentang fitur integrasinya dalam pelajaran Metode perubahan variabel dalam integral tak tentu.

Periksa: Bedakan jawabannya:

Fungsi integral asli telah diperoleh, artinya integral telah ditemukan dengan benar.
Selama verifikasi, kami harus mereduksi ekspresi menjadi penyebut yang sama, dan ini bukan suatu kebetulan. Metode koefisien tak tentu dan pengurangan ekspresi menjadi penyebut yang sama adalah tindakan yang saling bertolak belakang.

Contoh 2

Temukan integral tak tentu.

Mari kembali ke pecahan dari contoh pertama: . Sangat mudah untuk melihat bahwa dalam penyebut semua faktornya BERBEDA. Timbul pertanyaan, apa yang harus dilakukan jika, misalnya, diberikan pecahan berikut: ? Di sini kita mempunyai derajat dalam penyebutnya, atau, secara matematis, kelipatan. Selain itu, ada trinomial kuadrat yang tidak dapat difaktorkan (mudah untuk memverifikasi bahwa diskriminan persamaan tersebut negatif, sehingga trinomialnya tidak dapat difaktorkan). Apa yang harus dilakukan? Ekspansi ke dalam jumlah pecahan dasar akan terlihat seperti ini dengan koefisien yang tidak diketahui di atas atau yang lainnya?

Contoh 3

Perkenalkan sebuah fungsi

Langkah 1. Memeriksa apakah kita memiliki pecahan yang tepat
Pembilang utama: 2
Derajat penyebut tertinggi: 8
, yang berarti pecahannya benar.

Langkah 2. Apakah mungkin untuk memfaktorkan sesuatu pada penyebutnya? Tentu saja tidak, semua sudah diatur. Trinomial persegi tidak dapat diperluas menjadi produk karena alasan yang disebutkan di atas. Tudung. Lebih sedikit pekerjaan.

Langkah 3. Mari kita bayangkan fungsi pecahan-rasional sebagai penjumlahan dari pecahan dasar.
Dalam hal ini perluasannya mempunyai bentuk sebagai berikut:

Mari kita lihat penyebut kita:
Saat menguraikan fungsi pecahan-rasional menjadi jumlah pecahan dasar, tiga poin mendasar dapat dibedakan:

1) Jika penyebutnya mengandung faktor “kesepian” pangkat pertama (dalam kasus kita), maka kita letakkan koefisien tak tentu di atas (dalam kasus kita). Contoh No. 1, 2 hanya terdiri dari faktor-faktor “kesepian” tersebut.

2) Jika penyebutnya memiliki banyak pengganda, maka Anda perlu menguraikannya seperti ini:
- yaitu, secara berurutan melewati semua derajat "X" dari derajat pertama hingga ke-n. Dalam contoh kita, ada dua faktor ganda: dan , lihat lagi perluasan yang saya berikan dan pastikan bahwa perluasan tersebut persis sesuai dengan aturan ini.

3) Jika penyebutnya mengandung polinomial derajat kedua yang tidak dapat dikomposisi (dalam kasus kami), maka ketika menguraikan pembilangnya, Anda perlu menulis fungsi linier dengan koefisien yang tidak dapat ditentukan (dalam kasus kami dengan koefisien yang tidak dapat ditentukan dan ).

Sebenarnya ada kasus ke 4 lagi, tapi saya akan diam saja, karena dalam prakteknya sangat jarang.

Contoh 4

Perkenalkan sebuah fungsi sebagai jumlah pecahan dasar yang koefisiennya tidak diketahui.

Ini adalah contoh untuk Anda pecahkan sendiri. Solusi lengkap dan jawabannya di akhir pelajaran.
Ikuti algoritme dengan ketat!

Jika Anda memahami prinsip-prinsip yang diperlukan untuk memperluas fungsi rasional pecahan menjadi suatu penjumlahan, Anda dapat memahami hampir semua integral dari jenis yang sedang dipertimbangkan.

Contoh 5

Temukan integral tak tentu.

Langkah 1. Jelas pecahannya benar:

Langkah 2. Apakah mungkin untuk memfaktorkan sesuatu pada penyebutnya? Bisa. Berikut jumlah kubusnya . Faktorkan penyebutnya menggunakan rumus perkalian yang disingkat

Langkah 3. Dengan menggunakan metode koefisien tak tentu, kami memperluas integran menjadi jumlah pecahan dasar:

Harap dicatat bahwa polinomial tidak dapat difaktorkan (periksa apakah diskriminannya negatif), jadi di atas kita letakkan fungsi linier dengan koefisien yang tidak diketahui, dan bukan hanya satu huruf.

Kami membawa pecahan ke penyebut yang sama:

Mari menyusun dan menyelesaikan sistem:

(1) Kita nyatakan dari persamaan pertama dan substitusikan ke persamaan kedua sistem (ini adalah cara paling rasional).

(2) Kami menyajikan istilah serupa di persamaan kedua.

(3) Kita menjumlahkan persamaan kedua dan ketiga dari suku demi suku sistem.

Semua perhitungan lebih lanjut, pada prinsipnya, dilakukan secara lisan, karena sistemnya sederhana.

(1) Kita tuliskan jumlah pecahan sesuai dengan koefisien yang ditemukan.

(2) Kita menggunakan sifat linearitas integral tak tentu. Apa yang terjadi pada integral kedua? Anda dapat membiasakan diri dengan metode ini di paragraf terakhir pelajaran. Mengintegrasikan Beberapa Pecahan.

(3) Sekali lagi kita menggunakan sifat linearitas. Pada integral ketiga kita mulai mengisolasi persegi lengkap (paragraf kedua dari belakang pelajaran Mengintegrasikan Beberapa Pecahan).

(4) Kita ambil integral kedua, pada integral ketiga kita pilih kuadrat lengkapnya.

(5) Ambil integral ketiga. Siap.