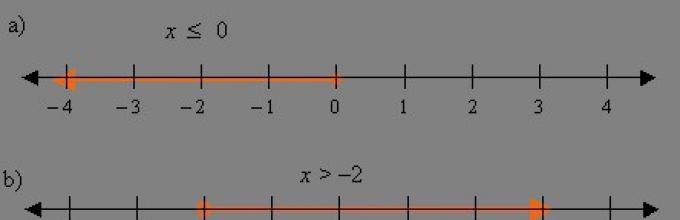Salah satu topik yang memerlukan perhatian dan ketekunan maksimal dari siswa adalah penyelesaian kesenjangan. Sangat mirip dengan persamaan dan pada saat yang sama sangat berbeda dari persamaan tersebut. Karena penyelesaiannya memerlukan pendekatan khusus.
Sifat-sifat yang diperlukan untuk menemukan jawabannya
Semuanya digunakan untuk mengganti entri yang sudah ada dengan entri yang setara. Kebanyakan dari mereka serupa dengan apa yang ada dalam persamaan. Namun ada juga perbedaan.
- Suatu fungsi yang didefinisikan dalam ODZ, atau bilangan apa pun, dapat dijumlahkan pada kedua ruas pertidaksamaan awal.
- Demikian pula, perkalian dapat dilakukan, tetapi hanya dengan fungsi atau bilangan positif.
- Jika tindakan ini dilakukan dengan fungsi atau bilangan negatif, maka tanda pertidaksamaan harus diganti dengan kebalikannya.
- Fungsi yang non-negatif dapat dipangkatkan positif.
Terkadang penyelesaian kesenjangan disertai dengan tindakan yang memberikan jawaban yang tidak relevan. Masalah tersebut perlu dihilangkan dengan membandingkan domain DL dan rangkaian solusi.
Menggunakan Metode Interval
Esensinya adalah mereduksi pertidaksamaan menjadi persamaan yang ruas kanannya ada nol.

- Tentukan area di mana nilai variabel yang diizinkan, yaitu ODZ, berada.
- Ubah pertidaksamaan tersebut menggunakan operasi matematika sehingga ruas kanannya bernilai nol.
- Gantikan tanda pertidaksamaan dengan “=” dan selesaikan persamaan yang sesuai.
- Pada sumbu numerik, tandai semua jawaban yang diperoleh selama penyelesaian, serta interval OD. Dalam kasus pertidaksamaan yang tegas, titik-titik tersebut harus digambarkan tertusuk. Jika ada tanda sama dengan, maka harus dicat ulang.
- Tentukan tanda fungsi awal pada setiap interval yang diperoleh dari titik-titik ODZ dan jawaban yang membaginya. Jika tanda suatu fungsi tidak berubah ketika melewati suatu titik, maka fungsi tersebut termasuk dalam jawabannya. Jika tidak, maka dikecualikan.
- Titik batas ODZ perlu dicek lebih lanjut baru kemudian dimasukkan atau tidak ke dalam jawaban.
- Jawaban yang dihasilkan harus ditulis dalam bentuk himpunan gabungan.
Sedikit tentang kesenjangan ganda
Mereka menggunakan dua tanda pertidaksamaan sekaligus. Artinya, beberapa fungsi dibatasi oleh kondisi dua kali sekaligus. Pertidaksamaan tersebut diselesaikan sebagai sistem dua, ketika pertidaksamaan asli dibagi menjadi beberapa bagian. Dan dalam metode interval, jawaban dari penyelesaian kedua persamaan ditunjukkan.
Untuk mengatasinya, diperbolehkan juga menggunakan properti yang disebutkan di atas. Dengan bantuan mereka, akan lebih mudah untuk mengurangi ketimpangan hingga nol.

Bagaimana dengan pertidaksamaan yang mempunyai modulus?
Dalam hal ini, penyelesaian pertidaksamaan menggunakan sifat-sifat berikut, dan sifat-sifat tersebut valid untuk nilai positif “a”.
Jika “x” berbentuk ekspresi aljabar, maka penggantian berikut ini valid:
- |x|< a на -a < х < a;
- |x| > a sampai x< -a или х >A.
Jika pertidaksamaannya tidak tegas, maka rumusnya juga benar, hanya saja di dalamnya, selain tanda besar atau kecil, muncul “=”.
Bagaimana cara mengatasi sistem kesenjangan?
Pengetahuan ini akan diperlukan jika tugas seperti itu diberikan atau ada catatan pertidaksamaan ganda atau modul muncul di catatan. Dalam situasi seperti ini, solusinya adalah nilai-nilai variabel yang memenuhi semua pertidaksamaan dalam catatan. Jika tidak ada angka seperti itu, maka sistem tidak memiliki solusi.
Rencana yang digunakan untuk menyelesaikan sistem pertidaksamaan:
- selesaikan masing-masing secara terpisah;
- gambarkan semua interval pada sumbu bilangan dan tentukan perpotongannya;
- tuliskan respons sistem, yang merupakan kombinasi dari apa yang terjadi di paragraf kedua.

Apa yang harus dilakukan dengan pertidaksamaan pecahan?
Karena penyelesaiannya mungkin memerlukan perubahan tanda pertidaksamaan, Anda harus mengikuti semua poin rencana dengan sangat hati-hati dan cermat. Jika tidak, Anda mungkin mendapatkan jawaban sebaliknya.
Penyelesaian pertidaksamaan pecahan juga menggunakan metode interval. Dan rencana aksinya adalah seperti ini:
- Dengan menggunakan sifat-sifat yang dijelaskan, berikan pecahan sedemikian rupa sehingga hanya tersisa nol di sebelah kanan tanda.
- Gantikan pertidaksamaan tersebut dengan “=” dan tentukan titik-titik dimana fungsinya akan sama dengan nol.
- Tandai mereka sumbu koordinat. Dalam hal ini, angka-angka yang diperoleh dari hasil perhitungan pada penyebutnya akan selalu dicoret. Semua yang lain didasarkan pada kondisi ketimpangan.
- Tentukan interval keteguhan tanda.
- Sebagai tanggapan, tuliskan gabungan interval-interval yang tandanya sesuai dengan pertidaksamaan awal.
Situasi ketika irasionalitas muncul dalam ketimpangan
Dengan kata lain, ada akar matematika dalam notasi tersebut. Sejak di kursus sekolah Dalam aljabar, sebagian besar tugas adalah untuk akar kuadrat, jadi inilah yang akan dipertimbangkan.
Larutan kesenjangan yang tidak rasional bermuara pada mendapatkan sistem dua atau tiga yang setara dengan yang asli.
| Ketimpangan asli | kondisi | sistem yang setara |
| √ n(x)< m(х) | m(x) kurang dari atau sama dengan 0 | tidak ada solusi |
| m(x) lebih besar dari 0 | n(x) lebih besar dari atau sama dengan 0 n(x)< (m(х)) 2 |
|
| √ n(x) > m(x) | m(x) lebih besar dari atau sama dengan 0 n(x) > (m(x)) 2 |
|
n(x) lebih besar dari atau sama dengan 0 m(x) kurang dari 0 |
||
| √n(x) ≤ m(x) | m(x) kurang dari 0 | tidak ada solusi |
| m(x) lebih besar dari atau sama dengan 0 | n(x) lebih besar dari atau sama dengan 0 n(x) ≤ (m(x)) 2 |
|
| √n(x) ≥ m(x) | m(x) lebih besar dari atau sama dengan 0 n(x) ≥ (m(x)) 2 |
|
n(x) lebih besar dari atau sama dengan 0 m(x) kurang dari 0 |
||
| √ n(x)< √ m(х) | n(x) lebih besar dari atau sama dengan 0 n(x) kurang dari m(x) |
|
| √n(x) * m(x)< 0 | n(x) lebih besar dari 0 m(x) kurang dari 0 |
|
| √n(x) * m(x) > 0 | n(x) lebih besar dari 0 m(x) lebih besar dari 0 |
|
| √n(x) * m(x) ≤ 0 | n(x) lebih besar dari 0 |
|
n(x) sama dengan 0 m(x) - apa saja |
||
| √n(x) * m(x) ≥ 0 | n(x) lebih besar dari 0 |
|
n(x) sama dengan 0 m(x) - apa saja |
Contoh penyelesaian berbagai jenis ketidaksetaraan
Untuk menambah kejelasan teori tentang penyelesaian pertidaksamaan, contoh diberikan di bawah ini.
Contoh pertama. 2x - 4 > 1 + x
Solusi: Untuk menentukan ADI, yang harus Anda lakukan hanyalah mencermati ketimpangan. Dibentuk dari fungsi linier, oleh karena itu didefinisikan untuk semua nilai variabel.
Sekarang Anda perlu mengurangi (1 + x) dari kedua sisi pertidaksamaan. Ternyata: 2x - 4 - (1 + x) > 0. Setelah tanda kurung dibuka dan suku-suku sejenisnya diberi, maka pertidaksamaannya berbentuk: x - 5 > 0.
Menyamakannya dengan nol, mudah untuk menemukan solusinya: x = 5.
Sekarang titik dengan angka 5 ini harus ditandai pada sinar koordinat. Kemudian periksa tanda-tanda fungsi aslinya. Pada interval pertama dari minus tak terhingga hingga 5, Anda dapat mengambil angka 0 dan mensubstitusikannya ke dalam pertidaksamaan yang diperoleh setelah transformasi. Setelah dihitung ternyata -7 >0. di bawah busur interval Anda perlu menandatangani tanda minus.
Pada interval selanjutnya dari 5 sampai tak terhingga, kamu bisa memilih angka 6. Maka ternyata 1 > 0. Ada tanda “+” di bawah busur. Interval kedua ini akan menjadi jawaban atas pertidaksamaan tersebut.
Jawaban: x terletak pada interval (5; ∞).

Contoh kedua. Diperlukan penyelesaian sistem dua persamaan: 3x + 3 ≤ 2x + 1 dan 3x - 2 ≤ 4x + 2.
Larutan. ODZ dari pertidaksamaan ini juga terletak pada wilayah bilangan berapapun, sejak diberikan fungsi linier.
Pertidaksamaan kedua berbentuk persamaan berikut: 3x - 2 - 4x - 2 = 0. Setelah transformasi: -x - 4 =0. Ini menghasilkan nilai variabel sama dengan -4.
Kedua angka ini perlu ditandai pada sumbu, yang menggambarkan interval. Karena pertidaksamaannya tidak ketat, semua titik perlu diarsir. Interval pertama adalah dari minus tak terhingga hingga -4. Biarkan angka -5 yang dipilih. Pertidaksamaan pertama bernilai -3, dan pertidaksamaan kedua bernilai 1. Artinya interval tersebut tidak termasuk dalam jawaban.
Interval kedua adalah dari -4 hingga -2. Anda dapat memilih angka -3 dan mensubstitusikannya ke kedua pertidaksamaan tersebut. Pada yang pertama dan kedua, nilainya -1. Artinya di bawah busur “-”.
Pada interval terakhir dari -2 hingga tak terhingga, bilangan terbaik adalah nol. Anda perlu menggantinya dan menemukan nilai pertidaksamaannya. Yang pertama menghasilkan bilangan positif, dan yang kedua menghasilkan nol. Kesenjangan ini juga harus dihilangkan dari jawabannya.
Dari ketiga interval tersebut, hanya satu yang merupakan solusi pertidaksamaan.
Jawaban: x milik [-4; -2].

Contoh ketiga. |1 - x| > 2 |x - 1|.
Larutan. Langkah pertama adalah menentukan titik hilangnya fungsi-fungsi tersebut. Untuk yang kiri angkanya adalah 2, untuk yang kanan - 1. Mereka perlu ditandai pada balok dan interval keteguhan tanda ditentukan.
Pada interval pertama, dari minus tak terhingga hingga 1, fungsi diambil dari ruas kiri pertidaksamaan nilai-nilai positif, dan dari kanan - negatif. Di bawah busur Anda perlu menulis dua tanda “+” dan “-” berdampingan.
Interval berikutnya adalah dari 1 hingga 2. Pada interval tersebut, kedua fungsi bernilai positif. Artinya ada dua nilai tambah di bawah busur.
Interval ketiga dari 2 hingga tak terhingga akan memberikan hasil sebagai berikut: fungsi kiri negatif, fungsi kanan positif.
Dengan mempertimbangkan tanda-tanda yang dihasilkan, Anda perlu menghitung nilai pertidaksamaan untuk semua interval.
Persamaan pertama menghasilkan pertidaksamaan sebagai berikut: 2 - x > - 2 (x - 1). Minus sebelum dua pada pertidaksamaan kedua disebabkan oleh fakta bahwa fungsi ini negatif.
Setelah transformasi, pertidaksamaannya terlihat seperti ini: x > 0. Ini langsung memberikan nilai variabel. Artinya, dari interval ini hanya interval 0 sampai 1 yang akan terjawab.
Yang kedua: 2 - x > 2 (x - 1). Transformasi tersebut menghasilkan pertidaksamaan berikut: -3x + 4 lebih besar dari nol. Nolnya adalah x = 4/3. Dengan memperhatikan tanda pertidaksamaan, ternyata x harus lebih kecil dari bilangan tersebut. Artinya interval ini dikurangi menjadi interval 1 hingga 4/3.
Persamaan terakhir memberikan pertidaksamaan berikut: - (2 - x) > 2 (x - 1). Transformasinya menghasilkan hal berikut: -x > 0. Artinya, persamaan tersebut benar jika x lebih kecil dari nol. Artinya pada interval yang diperlukan pertidaksamaan tersebut tidak memberikan solusi.
Pada dua interval pertama, angka pembatasnya ternyata 1. Perlu diperiksa secara terpisah. Artinya, substitusikan ke pertidaksamaan aslinya. Ternyata: |2 - 1| > 2 |1 - 1|. Penghitungan menunjukkan 1 lebih besar dari 0. Pernyataan tersebut benar, sehingga disertakan satu dalam jawabannya.
Jawaban: x terletak pada interval (0; 4/3).
Mengatasi kesenjangan secara online
Sebelum menyelesaikan pertidaksamaan, Anda harus memiliki pemahaman yang baik tentang cara menyelesaikan persamaan.
Tidak peduli apakah pertidaksamaannya ketat () atau tidak ketat (≤, ≥), langkah pertama yang harus dilakukan adalah menyelesaikan persamaan tersebut dengan mengganti tanda pertidaksamaan dengan persamaan (=).
Mari kita jelaskan apa yang dimaksud dengan menyelesaikan ketimpangan?
Setelah mempelajari persamaan, siswa mendapatkan gambaran berikut di kepalanya: dia perlu mencari nilai variabel sedemikian rupa sehingga kedua ruas persamaan mempunyai nilai yang sama. Dengan kata lain, temukan semua titik di mana kesetaraan berlaku. Semuanya benar!
Ketika kita berbicara tentang ketimpangan, yang kita maksud adalah mencari interval (segmen) yang menjadi tempat terjadinya ketimpangan. Jika terdapat dua variabel dalam pertidaksamaan tersebut, maka penyelesaiannya bukan lagi interval, melainkan beberapa luas pada bidang tersebut. Coba tebak sendiri apa solusi dari pertidaksamaan tiga variabel?
Bagaimana cara mengatasi kesenjangan?
Cara universal untuk menyelesaikan pertidaksamaan adalah dengan metode interval (juga dikenal sebagai metode interval), yang terdiri dari menentukan semua interval dalam batas-batas di mana pertidaksamaan tertentu akan dipenuhi.
Tanpa membahas jenis pertidaksamaan, dalam hal ini bukan intinya, Anda perlu menyelesaikan persamaan yang sesuai dan menentukan akar-akarnya, diikuti dengan menentukan solusi-solusi tersebut pada sumbu bilangan.
Bagaimana cara menulis penyelesaian pertidaksamaan dengan benar?
Setelah Anda menentukan interval penyelesaian pertidaksamaan, Anda perlu menuliskan penyelesaiannya dengan benar. Ada nuansa penting - apakah batas interval termasuk dalam solusi?
Semuanya sederhana di sini. Jika penyelesaian persamaan memenuhi ODZ dan pertidaksamaan tidak tegas, maka batas interval termasuk dalam penyelesaian pertidaksamaan tersebut. Jika tidak, tidak.
Dengan mempertimbangkan setiap interval, penyelesaian pertidaksamaan dapat berupa interval itu sendiri, atau setengah interval (jika salah satu batasnya memenuhi pertidaksamaan), atau segmen - interval beserta batas-batasnya.
Poin penting
Jangan berpikir bahwa hanya interval, setengah interval, dan segmen yang dapat menyelesaikan pertidaksamaan. Tidak, solusinya mungkin juga mencakup poin-poin individual.
Misalnya, pertidaksamaan |x|≤0 hanya memiliki satu solusi - yaitu titik 0.
Dan pertidaksamaan |x|
Mengapa Anda memerlukan kalkulator pertidaksamaan?
Kalkulator pertidaksamaan memberikan jawaban akhir yang benar. Dalam kebanyakan kasus, ilustrasi sumbu atau bidang bilangan disediakan. Terlihat apakah batas-batas interval termasuk dalam solusi atau tidak - titik-titik ditampilkan sebagai berbayang atau tertusuk.
Terimakasih untuk kalkulator daring pertidaksamaan, Anda dapat memeriksa apakah Anda telah menemukan akar-akar persamaan dengan benar, menandainya pada sumbu bilangan, dan memeriksa terpenuhinya kondisi pertidaksamaan pada interval (dan batas)?
Jika jawaban Anda berbeda dengan jawaban kalkulator, maka Anda perlu memeriksa ulang solusi Anda dan mengidentifikasi kesalahannya.
Setelah menerima informasi awal tentang pertidaksamaan dengan variabel, kita beralih ke pertanyaan tentang penyelesaiannya. Kami akan menganalisis solusi pertidaksamaan linier dengan satu variabel dan semua metode penyelesaiannya dengan algoritma dan contoh. Hanya persamaan linear dengan satu variabel yang akan dipertimbangkan.
Apa itu ketimpangan linier?
Pertama, Anda perlu mendefinisikan persamaan linier dan mencari tahu bentuk standarnya serta perbedaannya dari persamaan lainnya. Dari pembelajaran di sekolah kita mengetahui bahwa tidak ada perbedaan mendasar antara ketimpangan, sehingga perlu menggunakan beberapa definisi.
Definisi 1
Ketimpangan linier dengan satu variabel x adalah pertidaksamaan berbentuk a · x + b > 0, bila ada tanda pertidaksamaan yang digunakan sebagai pengganti >< , ≤ , ≥ , а и b являются действительными числами, где a ≠ 0 .
Definisi 2
Pertidaksamaan ax< c или a · x >c, dengan x sebagai variabel dan a dan c sebagai bilangan, disebut pertidaksamaan linier dengan satu variabel.
Karena tidak ada yang dikatakan tentang apakah koefisiennya bisa sama dengan 0, maka pertidaksamaan tegas berbentuk 0 x > c dan 0 x< c может быть записано в виде нестрогого, а именно, a · x ≤ c , a · x ≥ c . Такое уравнение считается линейным.
Perbedaan mereka adalah:
- bentuk notasi a · x + b > 0 pada notasi pertama, dan a · x > c – pada notasi kedua;
- diterimanya koefisien a sama dengan nol, a ≠ 0 - pada yang pertama, dan a = 0 - pada yang kedua.
Pertidaksamaan a · x + b > 0 dan a · x > c dianggap ekuivalen, karena diperoleh dengan memindahkan suku dari satu bagian ke bagian lain. Menyelesaikan pertidaksamaan 0 x + 5 > 0 akan mengakibatkan pertidaksamaan tersebut perlu diselesaikan, dan kasus a = 0 tidak akan berhasil.
Definisi 3
Pertidaksamaan linier pada satu variabel x dianggap merupakan pertidaksamaan bentuk a x + b< 0 , a · x + b >0, ax + b ≤ 0 Dan a x + b ≥ 0, dimana a dan b adalah bilangan real. Alih-alih x, bisa ada angka biasa.
Berdasarkan aturan tersebut, kita mendapatkan bahwa 4 x − 1 > 0, 0 z + 2, 3 ≤ 0, - 2 3 x - 2< 0 являются примерами линейных неравенств. А неравенства такого плана, как 5 · x >7 , − 0 , 5 · y ≤ − 1 , 2 disebut dapat direduksi menjadi linier.
Cara mengatasi pertidaksamaan linier
Cara utama untuk menyelesaikan pertidaksamaan tersebut adalah dengan menggunakan transformasi ekuivalen untuk mencari pertidaksamaan elementer x< p (≤ , >, ≥) , p yang merupakan bilangan tertentu, untuk a ≠ 0, dan berbentuk a< p (≤ , >, ≥) untuk a = 0.
Untuk menyelesaikan pertidaksamaan dalam satu variabel, Anda dapat menggunakan metode interval atau merepresentasikannya secara grafis. Salah satu dari mereka dapat digunakan secara terpisah.
Menggunakan transformasi yang setara
Menyelesaikan pertidaksamaan linier berbentuk a x + b< 0 (≤ , >, ≥), maka perlu diterapkan transformasi pertidaksamaan ekuivalen. Koefisiennya mungkin nol atau tidak. Mari kita pertimbangkan kedua kasus tersebut. Untuk mengetahuinya, Anda harus mengikuti skema yang terdiri dari 3 poin: esensi proses, algoritma, dan solusi itu sendiri.
Definisi 4
Algoritma untuk menyelesaikan pertidaksamaan linier a x + b< 0 (≤ , >, ≥) untuk ≠ 0
- bilangan b akan dipindahkan ke ruas kanan pertidaksamaan yang bertanda berlawanan, sehingga kita dapat memperoleh persamaan a x< − b (≤ , > , ≥) ;
- Kedua ruas pertidaksamaan tersebut akan dibagi dengan angka yang tidak sama dengan 0. Selain itu, bila a bernilai positif, tandanya tetap ada; bila a bernilai negatif, maka tandanya berubah menjadi sebaliknya.
Mari kita pertimbangkan penerapan algoritma ini untuk menyelesaikan contoh.
Contoh 1
Selesaikan pertidaksamaan bentuk 3 x + 12 ≤ 0.
Larutan
Pertidaksamaan linier ini memiliki a = 3 dan b = 12. Artinya koefisien a dari x tidak sama dengan nol. Mari terapkan algoritma di atas dan selesaikan.
Suku 12 perlu dipindahkan ke bagian lain pertidaksamaan dan mengubah tanda di depannya. Kemudian kita mendapatkan pertidaksamaan berbentuk 3 x ≤ − 12. Kedua bagian harus dibagi 3. Tandanya tidak akan berubah karena 3 adalah bilangan positif. Kita mendapatkan (3 x) : 3 ≤ (− 12) : 3, sehingga menghasilkan x ≤ − 4.
Pertidaksamaan berbentuk x ≤ − 4 adalah ekuivalen. Artinya, penyelesaian untuk 3 x + 12 ≤ 0 adalah sembarang bilangan real, yang kurang dari atau sama dengan 4. Jawabannya ditulis sebagai pertidaksamaan x ≤ − 4, atau interval numerik dalam bentuk (− ∞, − 4].
Seluruh algoritma yang dijelaskan di atas ditulis seperti ini:
3 x + 12 ≤ 0 ; 3 x ≤ − 12 ; x ≤ − 4 .
Menjawab: x ≤ − 4 atau (− ∞ , − 4 ] .
Contoh 2
Tunjukkan semua solusi yang tersedia untuk pertidaksamaan − 2, 7 · z > 0.
Larutan
Dari kondisi tersebut kita melihat bahwa koefisien a untuk z sama dengan - 2,7, dan b jelas tidak ada atau sama dengan nol. Anda tidak dapat menggunakan langkah pertama dari algoritme, tetapi segera melanjutkan ke langkah kedua.
Kami membagi kedua ruas persamaan dengan angka - 2, 7. Karena angkanya negatif, maka tanda pertidaksamaannya perlu dibalik. Artinya, kita mendapatkan (− 2, 7 z) : (− 2, 7)< 0: (− 2 , 7) , и дальше z < 0 .
Mari kita tuliskan keseluruhan algoritma dalam bentuk singkat:
− 2, 7 z > 0; z< 0 .
Menjawab: z< 0 или (− ∞ , 0) .
Contoh 3
Selesaikan pertidaksamaan - 5 x - 15 22 ≤ 0.
Larutan
Berdasarkan kondisi tersebut, kita melihat bahwa pertidaksamaan dengan koefisien a untuk variabel x, yang sama dengan - 5, perlu diselesaikan dengan koefisien b, yang sesuai dengan pecahan - 15 22. Penyelesaian pertidaksamaan harus dilakukan dengan mengikuti algoritma, yaitu: pindahkan - 15 22 ke bagian lain yang bertanda berlawanan, bagi kedua bagian dengan - 5, ubah tanda pertidaksamaan:
5x ≤ 15 22 ; - 5 x: - 5 ≥ 15 22: - 5 x ≥ - 3 22
Pada transisi terakhir untuk ruas kanan, digunakan aturan pembagian bilangan dengan tanda yang berbeda 15 22: - 5 = - 15 22: 5, setelah itu kita melakukan pembagian pecahan biasa ke bilangan asli - 15 22: 5 = - 15 22 · 1 5 = - 15 · 1 22 · 5 = - 3 22 .
Menjawab: x ≥ - 3 22 dan [ - 3 22 + ∞) .
Mari kita perhatikan kasus ketika a = 0. Ekspresi linier bentuk a x + b< 0 является неравенством 0 · x + b < 0 , где на рассмотрение берется неравенство вида b < 0 , после чего выясняется, оно верное или нет.
Semuanya didasarkan pada penentuan solusi pertidaksamaan tersebut. Untuk setiap nilai x kita memperoleh pertidaksamaan numerik dalam bentuk b< 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b < 0 , где b < 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b < 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Kami akan mempertimbangkan semua penilaian dalam bentuk algoritma untuk menyelesaikan pertidaksamaan linier 0 x + b< 0 (≤ , > , ≥) :
Definisi 5
Bentuk pertidaksamaan numerik b< 0 (≤ , >, ≥) benar, maka pertidaksamaan awal mempunyai solusi untuk nilai apa pun, dan salah jika pertidaksamaan awal tidak memiliki solusi.
Contoh 4
Selesaikan pertidaksamaan 0 x + 7 > 0.
Larutan
Pertidaksamaan linier 0 x + 7 > 0 ini dapat bernilai x berapa pun. Kemudian kita mendapatkan pertidaksamaan berbentuk 7 > 0. Pertidaksamaan terakhir dianggap benar, artinya bilangan berapa pun bisa menjadi penyelesaiannya.
Menjawab: interval (− ∞ , + ∞) .
Contoh 5
Temukan solusi pertidaksamaan 0 x − 12, 7 ≥ 0.
Larutan
Saat mensubstitusi variabel x dari bilangan apa pun, kita memperoleh bahwa pertidaksamaan berbentuk − 12, 7 ≥ 0. Itu tidak benar. Artinya, 0 x − 12, 7 ≥ 0 tidak mempunyai penyelesaian.
Menjawab: tidak ada solusi.
Mari kita pertimbangkan penyelesaian pertidaksamaan linier yang kedua koefisiennya sama dengan nol.
Contoh 6
Tentukan pertidaksamaan tak terselesaikan dari 0 x + 0 > 0 dan 0 x + 0 ≥ 0.
Larutan
Saat mensubstitusi bilangan apa pun selain x, kita memperoleh dua pertidaksamaan berbentuk 0 > 0 dan 0 ≥ 0. Yang pertama salah. Artinya 0 x + 0 > 0 tidak mempunyai solusi, dan 0 x + 0 ≥ 0 mempunyai jumlah solusi yang tak terhingga, yaitu bilangan berapa pun.
Menjawab: pertidaksamaan 0 x + 0 > 0 tidak mempunyai penyelesaian, tetapi 0 x + 0 ≥ 0 mempunyai penyelesaian.
Metode ini dibahas dalam mata pelajaran matematika sekolah. Metode interval mampu menyelesaikan berbagai jenis pertidaksamaan, termasuk pertidaksamaan linier.
Metode interval digunakan untuk pertidaksamaan linier bila nilai koefisien x tidak sama dengan 0. Jika tidak, Anda harus menghitung menggunakan metode lain.
Definisi 6
Metode intervalnya adalah:
- memperkenalkan fungsi y = a · x + b ;
- mencari angka nol untuk membagi domain definisi menjadi beberapa interval;
- definisi tanda untuk konsep mereka tentang interval.
Mari kita menyusun algoritma untuk menyelesaikan persamaan linear ax + b< 0 (≤ , >, ≥) untuk a ≠ 0 menggunakan metode interval:
- mencari nol dari fungsi y = a · x + b untuk menyelesaikan persamaan bentuk a · x + b = 0 . Jika a ≠ 0, maka solusinya adalah akar tunggal, yang diberi notasi x 0;
- konstruksi garis koordinat yang menggambarkan suatu titik dengan koordinat x 0, dengan pertidaksamaan tegas titik tersebut dilambangkan dengan pertidaksamaan tak tegas – dengan pertidaksamaan tegas;
- menentukan tanda-tanda fungsi y = a · x + b pada interval, untuk itu perlu mencari nilai fungsi pada titik-titik pada interval;
- menyelesaikan pertidaksamaan dengan tanda > atau ≥ pada garis koordinat, menambahkan bayangan pada interval positif,< или ≤ над отрицательным промежутком.
Mari kita lihat beberapa contoh penyelesaian pertidaksamaan linier menggunakan metode interval.
Contoh 6
Selesaikan pertidaksamaan − 3 x + 12 > 0.
Larutan
Berdasarkan algoritma tersebut, pertama-tama Anda perlu mencari akar persamaan − 3 x + 12 = 0. Kita peroleh bahwa − 3 · x = − 12 , x = 4 . Kita perlu menggambar garis koordinat tempat kita menandai titik 4. Ini akan tertusuk karena ketimpangan yang sangat ketat. Perhatikan gambar di bawah ini.
Penting untuk menentukan tanda-tanda pada intervalnya. Untuk menentukannya pada interval (− ∞, 4), perlu dihitung fungsi y = − 3 x + 12 pada x = 3. Dari sini kita peroleh bahwa − 3 3 + 12 = 3 > 0. Tanda pada interval tersebut positif.
Kita tentukan tandanya dari interval (4, + ∞), lalu substitusikan nilai x = 5. Kita mempunyai − 3 5 + 12 = − 3< 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
![]()
Kami menyelesaikan pertidaksamaan dengan tanda >, dan bayangan dilakukan pada interval positif. Perhatikan gambar di bawah ini.
![]()
Dari gambar terlihat jelas bahwa solusi yang diinginkan berbentuk (− ∞ , 4) atau x< 4 .
Menjawab: (− ∞ , 4) atau x< 4 .
Untuk memahami cara menggambarkannya secara grafis, perlu diperhatikan 4 pertidaksamaan linier sebagai contoh: 0, 5 x − 1< 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 >0 dan 0, 5 x − 1 ≥ 0. Solusinya adalah nilai x< 2 , x ≤ 2 , x >2 dan x ≥ 2. Untuk melakukannya, mari kita plot fungsi linier y = 0, 5 x − 1 seperti yang ditunjukkan di bawah ini.

Sudah jelas itu
Definisi 7
- menyelesaikan pertidaksamaan 0, 5 x − 1< 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х;
- solusi 0, 5 x − 1 ≤ 0 dianggap sebagai interval di mana fungsi y = 0, 5 x − 1 lebih rendah dari O x atau bertepatan;
- solusinya 0, 5 · x − 1 > 0 dianggap sebagai interval, fungsinya terletak di atas O x;
- solusi 0, 5 · x − 1 ≥ 0 dianggap sebagai interval dimana grafik di atas O x atau bertepatan.
Arti solusi grafis pertidaksamaan adalah mencari interval yang harus digambarkan dalam grafik. Dalam hal ini, kita menemukan bahwa ruas kiri mempunyai y = a · x + b, dan ruas kanan mempunyai y = 0, dan berimpit dengan O x.
Definisi 8Grafik fungsi y = a x + b diplot:
- sambil menyelesaikan pertidaksamaan a x + b< 0 определяется промежуток, где график изображен ниже О х;
- ketika menyelesaikan pertidaksamaan a · x + b ≤ 0, interval ditentukan jika grafik digambarkan di bawah sumbu O x atau bertepatan;
- ketika menyelesaikan pertidaksamaan a · x + b > 0, intervalnya ditentukan di mana grafik digambarkan di atas O x;
- Saat menyelesaikan pertidaksamaan a · x + b ≥ 0, interval ditentukan jika grafiknya berada di atas O x atau bertepatan.
Contoh 7
Selesaikan pertidaksamaan - 5 · x - 3 > 0 menggunakan grafik.
Larutan
Perlu dibuat grafik fungsi linier - 5 · x - 3 > 0. Garis ini menurun karena koefisien x negatif. Untuk menentukan koordinat titik potongnya dengan O x - 5 · x - 3 > 0, kita peroleh nilai - 3 5. Mari kita gambarkan secara grafis.

Menyelesaikan pertidaksamaan dengan tanda >, maka perlu memperhatikan interval di atas O x. Mari kita sorot bagian pesawat yang diperlukan dengan warna merah dan dapatkan itu

Celah yang dibutuhkan adalah bagian O x merah. Artinya sinar bilangan terbuka - ∞ , - 3 5 merupakan penyelesaian pertidaksamaan tersebut. Jika menurut kondisi kita mempunyai pertidaksamaan tidak tegas, maka nilai titik - 3 5 juga merupakan penyelesaian pertidaksamaan tersebut. Dan itu akan bertepatan dengan O x.
Menjawab: - ∞ , - 3 5 atau x< - 3 5 .
Metode grafis penyelesaian digunakan jika ruas kiri sesuai dengan fungsi y = 0 x + b, yaitu y = b. Maka garis lurus tersebut akan sejajar dengan O x atau bertepatan di b = 0. Kasus-kasus ini menunjukkan bahwa pertidaksamaan tersebut mungkin tidak mempunyai solusi, atau solusinya bisa berupa bilangan berapa pun.
Contoh 8
Tentukan dari pertidaksamaan 0 x + 7< = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.
Larutan
Representasi y = 0 x + 7 adalah y = 7, maka akan diberikan bidang koordinat dengan garis lurus sejajar O x dan terletak di atas O x. Jadi 0x+7< = 0 решений не имеет, потому как нет промежутков.
Grafik fungsi y = 0 x + 0 dianggap y = 0, yaitu garis lurus berimpit dengan O x. Artinya pertidaksamaan 0 x + 0 ≥ 0 mempunyai banyak penyelesaian.
Menjawab: Pertidaksamaan kedua mempunyai solusi untuk sembarang nilai x.
Ketimpangan yang mereduksi menjadi linear
Solusi terhadap kesenjangan dapat direduksi menjadi solusi persamaan linier, yang disebut pertidaksamaan yang direduksi menjadi linier.
Ketimpangan ini dipertimbangkan dalam kursus sekolah, karena merupakan kasus khusus untuk menyelesaikan ketidaksetaraan, yang menyebabkan pembukaan tanda kurung dan pengurangan suku serupa. Misalnya, anggaplah 5 − 2 x > 0, 7 (x − 1) + 3 ≤ 4 x − 2 + x, x - 3 5 - 2 x + 1 > 2 7 x.
Pertidaksamaan yang diberikan di atas selalu direduksi menjadi bentuk persamaan linier. Setelah itu, tanda kurung dibuka dan suku-suku serupa diberikan, dipindahkan dari bagian yang berbeda, mengubah tandanya menjadi sebaliknya.
Saat mereduksi pertidaksamaan 5 − 2 x > 0 menjadi linier, kita nyatakan sedemikian rupa sehingga berbentuk − 2 x + 5 > 0, dan untuk mereduksi per detik kita peroleh bahwa 7 (x − 1) + 3 ≤ 4 x − 2 + x . Anda perlu membuka tanda kurung, membawa suku-suku serupa, memindahkan semua suku ke sisi kiri dan membawa suku-suku serupa. Ini terlihat seperti ini:
7 x − 7 + 3 ≤ 4 x − 2 + x 7 x − 4 ≤ 5 x − 2 7 x − 4 − 5 x + 2 ≤ 0 2 x − 2 ≤ 0
Hal ini menyebabkan penyelesaiannya menjadi pertidaksamaan linier.
Pertidaksamaan ini dianggap linier, karena mempunyai prinsip penyelesaian yang sama, setelah itu dapat direduksi menjadi pertidaksamaan elementer.
Untuk mengatasi pertidaksamaan jenis ini, perlu direduksi menjadi pertidaksamaan linier. Ini harus dilakukan dengan cara ini:
Definisi 9
- buka tanda kurung;
- kumpulkan variabel di sebelah kiri dan angka di sebelah kanan;
- berikan istilah serupa;
- bagi kedua ruas dengan koefisien x.
Contoh 9
Selesaikan pertidaksamaan 5 · (x + 3) + x ≤ 6 · (x − 3) + 1.
Larutan
Kita buka tanda kurungnya, lalu kita peroleh pertidaksamaan berbentuk 5 x + 15 + x ≤ 6 x − 18 + 1. Setelah mereduksi suku-suku serupa, kita mendapatkan 6 x + 15 ≤ 6 x − 17. Setelah memindahkan suku dari kiri ke kanan, kita mendapatkan bahwa 6 x + 15 − 6 x + 17 ≤ 0. Jadi terdapat pertidaksamaan berbentuk 32 ≤ 0 dari pertidaksamaan yang diperoleh dengan menghitung 0 x + 32 ≤ 0. Terlihat bahwa pertidaksamaan tersebut salah, artinya pertidaksamaan yang diberikan oleh kondisi tidak memiliki solusi.
Menjawab: tidak ada solusi.
Perlu dicatat bahwa ada banyak jenis pertidaksamaan lain yang dapat direduksi menjadi pertidaksamaan linier atau seperti yang ditunjukkan di atas. Misalnya, 5 2 x − 1 ≥ 1 adalah persamaan eksponensial, yang direduksi menjadi solusi linier 2 x − 1 ≥ 0 . Kasus-kasus ini akan dipertimbangkan ketika menyelesaikan pertidaksamaan jenis ini.
Jika Anda melihat kesalahan pada teks, silakan sorot dan tekan Ctrl+Enter
solusi ketimpangan dalam mode on line larutan hampir semua ketimpangan tertentu on line. Matematis kesenjangan secara online untuk menyelesaikan matematika. Temukan dengan cepat solusi ketimpangan dalam mode on line. Situs web www.site memungkinkan Anda menemukan larutan hampir semua diberikan aljabar, trigonometri atau kesenjangan transendental secara online. Saat mempelajari hampir semua cabang matematika di tahapan yang berbeda harus memutuskan kesenjangan secara online. Untuk mendapatkan jawaban segera, dan yang terpenting jawaban akurat, Anda memerlukan sumber daya yang memungkinkan Anda melakukan hal tersebut. Berkat situs www.site menyelesaikan ketimpangan secara online akan memakan waktu beberapa menit. Keuntungan utama www.site saat menyelesaikan matematika kesenjangan secara online- ini adalah kecepatan dan keakuratan respon yang diberikan. Situs ini mampu menyelesaikan masalah apa pun pertidaksamaan aljabar online, pertidaksamaan trigonometri online, kesenjangan transendental secara online, Dan kesenjangan dengan parameter yang tidak diketahui dalam mode on line. Ketimpangan berfungsi sebagai alat matematika yang kuat solusi masalah praktis. Dengan bantuan ketidaksetaraan matematika adalah mungkin untuk mengungkapkan fakta dan hubungan yang mungkin tampak membingungkan dan rumit pada pandangan pertama. Jumlah yang tidak diketahui kesenjangan dapat ditemukan dengan merumuskan masalah pada matematis bahasa dalam bentuk kesenjangan Dan memutuskan menerima tugas dalam mode on line di situs web www.site. Setiap pertidaksamaan aljabar, pertidaksamaan trigonometri atau kesenjangan mengandung teramat fitur yang Anda dapat dengan mudah memutuskan online dan dapatkan jawaban pastinya. Mempelajari ilmu pengetahuan Alam, Anda pasti menghadapi kebutuhan tersebut solusi terhadap kesenjangan. Dalam hal ini, jawabannya harus akurat dan harus segera diperoleh dalam mode tersebut on line. Oleh karena itu untuk menyelesaikan pertidaksamaan matematika secara online kami merekomendasikan situs www.site, yang akan menjadi kalkulator yang sangat diperlukan untuk Anda menyelesaikan pertidaksamaan aljabar secara online, pertidaksamaan trigonometri on line, Dan kesenjangan transendental secara online atau kesenjangan dengan parameter yang tidak diketahui. Untuk masalah praktis menemukan solusi online yang beragam ketidaksetaraan matematika sumber daya www.. Pemecahan kesenjangan secara online sendiri, akan berguna untuk memeriksa jawaban yang diterima menggunakan solusi daring kesenjangan di situs web www.site. Anda perlu menulis pertidaksamaan dengan benar dan langsung mendapatkannya solusi daring, setelah itu yang tersisa hanyalah membandingkan jawabannya dengan solusi pertidaksamaan Anda. Mengecek jawabannya tidak lebih dari satu menit, itu sudah cukup menyelesaikan kesenjangan secara online dan bandingkan jawabannya. Ini akan membantu Anda menghindari kesalahan dalam keputusan dan perbaiki jawabannya pada waktunya menyelesaikan kesenjangan secara online salah satu aljabar, trigonometri, teramat atau ketidaksamaan dengan parameter yang tidak diketahui.
Ketimpangan disebut linier ruas kiri dan kanannya merupakan fungsi linier terhadap besaran yang tidak diketahui. Hal ini misalnya mencakup kesenjangan:
2x-1-x+3; 7x0;
5 >4 - 6x 9- X< x + 5 .
1) Ketimpangan yang ketat: kapak +b>0 atau kapak+b<0
2) Ketimpangan yang tidak ketat: kapak +b≤0 atau kapak+b≫ 0
Mari kita menganalisis tugas ini. Salah satu sisi jajar genjang adalah 7 cm. Berapa panjang sisi yang lain agar keliling jajar genjang lebih besar dari 44 cm?
Biarkan sisi yang diperlukan menjadi X cm, keliling jajar genjang dinyatakan dengan (14 + 2x) cm, pertidaksamaan 14 + 2x > 44 adalah model matematika soal keliling jajar genjang. Jika kita mengganti variabel pada pertidaksamaan ini X misalnya pada bilangan 16, maka diperoleh pertidaksamaan numerik yang benar 14 + 32 > 44. Dalam hal ini dikatakan bahwa bilangan 16 merupakan penyelesaian pertidaksamaan 14 + 2x > 44.
Memecahkan ketimpangan sebutkan nilai suatu variabel yang mengubahnya menjadi pertidaksamaan numerik yang sebenarnya.
Jadi, masing-masing bilangan tersebut adalah 15,1; 20;73 merupakan penyelesaian pertidaksamaan 14 + 2x > 44, tetapi bilangan 10, misalnya, bukanlah penyelesaiannya.
Selesaikan ketimpangan berarti menetapkan semua solusinya atau membuktikan bahwa tidak ada solusi.
Rumusan penyelesaian pertidaksamaan serupa dengan rumusan akar persamaan. Namun bukanlah hal yang lazim untuk menyebut “akar ketimpangan”.
Sifat-sifat persamaan numerik membantu kita memecahkan persamaan. Properti yang persis sama ketidaksetaraan numerik membantu mengatasi kesenjangan.
Saat menyelesaikan suatu persamaan, kita mengubahnya ke persamaan lain yang lebih banyak persamaan sederhana, tetapi setara dengan yang diberikan. Jawaban terhadap kesenjangan ditemukan dengan cara yang sama. Saat mengubah suatu persamaan menjadi persamaan ekuivalen, mereka menggunakan teorema tentang memindahkan suku-suku dari satu ruas persamaan ke ruas yang berlawanan dan tentang mengalikan kedua ruas persamaan dengan bilangan bukan nol yang sama. Saat menyelesaikan pertidaksamaan, terdapat perbedaan yang signifikan antara pertidaksamaan dan persamaan, yaitu bahwa setiap penyelesaian persamaan dapat diverifikasi hanya dengan substitusi ke persamaan aslinya. Dalam pertidaksamaan, metode ini tidak ada karena tidak mungkin untuk mensubstitusi solusi yang tak terhitung jumlahnya ke dalam pertidaksamaan awal. Oleh karena itu, ada konsep penting yaitu anak panah tersebut<=>adalah tanda transformasi yang setara, atau setara. Transformasi tersebut disebut setara, atau setara, jika mereka tidak mengubah rangkaian solusi.
Aturan serupa untuk menyelesaikan kesenjangan.
Jika kita memindahkan suatu suku dari satu bagian pertidaksamaan ke bagian pertidaksamaan lainnya, mengganti tandanya dengan tanda yang berlawanan, kita memperoleh pertidaksamaan yang ekuivalen dengan pertidaksamaan tersebut.
Jika kedua ruas pertidaksamaan dikalikan (dibagi) dengan bilangan positif yang sama, kita memperoleh pertidaksamaan yang ekuivalen dengan bilangan tersebut.
Jika kedua ruas pertidaksamaan dikalikan (dibagi) dengan bilangan negatif yang sama, dan mengganti tanda pertidaksamaan dengan tanda pertidaksamaan yang berlawanan, kita memperoleh pertidaksamaan yang ekuivalen dengan pertidaksamaan tersebut.
Menggunakan ini aturan Mari kita hitung pertidaksamaan berikut.
1) Mari kita analisis ketimpangan tersebut 2x - 5 > 9.
Ini ketimpangan linier, kita akan mencari solusinya dan membahas konsep dasarnya.
2x - 5 > 9<=>2x>14(5 dipindahkan ke sisi kiri dengan tanda berlawanan), lalu kita bagi semuanya dengan 2 dan kita punya x > 7. Mari kita plot himpunan solusi pada sumbu X
Kami telah memperoleh sinar yang diarahkan secara positif. Kami mencatat himpunan solusi baik dalam bentuk pertidaksamaan x > 7, atau dalam bentuk interval x(7; ∞). Apa solusi khusus untuk mengatasi kesenjangan ini? Misalnya, x = 10 adalah solusi khusus untuk ketimpangan ini, x = 12- ini juga merupakan solusi khusus untuk ketimpangan ini.
Ada banyak solusi parsial, namun tugas kita adalah menemukan semua solusi. Dan biasanya ada banyak sekali solusi.
Mari kita selesaikan contoh 2:
2) Mengatasi ketimpangan 4a - 11 > a+13.
Mari kita selesaikan: A pindahkan ke satu sisi 11 pindahkan ke sisi lain, kita mendapatkan 3a< 24, и в результате после деления обеих частей на 3 ketidaksetaraan memiliki bentuk A<8 .
4a - 11 > a+13<=>3a< 24 <=>A< 8 .
Kami juga akan menampilkan setnya A< 8 , tapi sudah di poros A.
Jawabannya bisa kita tuliskan dalam bentuk pertidaksamaan a< 8, либо A(-∞;8), 8 tidak menyala.