Fungsikamu = dosaX
Grafik fungsinya adalah sinusoidal.
Bagian lengkap gelombang sinus yang tidak berulang disebut gelombang sinus.
Setengah gelombang sinus disebut setengah gelombang sinus (atau busur).
Properti Fungsikamu =
dosaX:
3) Ini adalah fungsi ganjil. 4) Ini fungsi berkelanjutan.
6) Pada ruas [-π/2; fungsi π/2] bertambah pada interval [π/2; 3π/2] – berkurang. 7) Pada interval fungsi tersebut berlangsung nilai-nilai positif. 8) Interval kenaikan fungsi: [-π/2 + 2πn; π/2 + 2πn]. 9) Titik minimum fungsi: -π/2 + 2πn. |
Untuk membuat grafik suatu fungsi kamu= dosa X Lebih mudah menggunakan skala berikut:
Pada selembar kertas yang berbentuk persegi, kita ambil panjang dua persegi sebagai satuan ruas.
Pada sumbu X Mari kita ukur panjangnya π. Pada saat yang sama, untuk memudahkan, kami menyajikan 3,14 sebagai 3 - yaitu, tanpa pecahan. Kemudian pada selembar kertas dalam satu sel π akan ada 6 sel (tiga kali 2 sel). Dan setiap sel akan menerima nama aslinya sendiri (dari yang pertama hingga keenam): π/6, π/3, π/2, 2π/3, 5π/6, π. Inilah maknanya X.
Pada sumbu y kita tandai 1, yang mencakup dua sel.
Mari buat tabel nilai fungsi menggunakan nilai kita X:
√3 | √3 |
Selanjutnya kita akan membuat jadwal. Ini akan menjadi setengah gelombang, titik tertinggi yang (π/2; 1). Ini adalah grafik fungsinya kamu= dosa X pada segmen tersebut. Mari kita tambahkan setengah gelombang simetris ke grafik yang dibangun (simetris terhadap titik asal, yaitu pada segmen -π). Puncak setengah gelombang ini berada di bawah sumbu x dengan koordinat (-1; -1). Hasilnya akan menjadi gelombang. Ini adalah grafik fungsinya kamu= dosa X pada segmen [-π; π].
Anda dapat melanjutkan gelombang dengan membangunnya pada segmen [π; 3π], [π; 5π], [π; 7π], dll. Pada semua segmen tersebut, grafik fungsinya akan terlihat sama seperti pada segmen [-π; π]. Anda akan mendapatkan garis bergelombang terus menerus dengan gelombang yang identik.
Fungsikamu = karenaX.
Grafik suatu fungsi adalah gelombang sinus (kadang-kadang disebut gelombang kosinus).

Properti Fungsikamu = karenaX:
1) Daerah definisi suatu fungsi adalah himpunan bilangan real. 2) Rentang nilai fungsi adalah segmen [–1; 1] 3) Ini adalah fungsi genap. 4) Ini adalah fungsi berkelanjutan. 5) Koordinat titik potong grafik: 6) Pada ruas fungsinya menurun, pada ruas [π; 2π] – meningkat. 7) Pada interval [-π/2 + 2πn; Fungsi π/2 + 2πn] bernilai positif. 8) Peningkatan interval: [-π + 2πn; 2πn]. 9) Poin minimum dari fungsi: π + 2πn. 10) Fungsinya dibatasi dari atas dan bawah. Nilai terendah fungsi –1, 11) Ini fungsi periodik dengan periode 2π (T = 2π) |
Fungsikamu = mf(X).
Mari kita ambil fungsi sebelumnya kamu= karena X. Seperti yang sudah Anda ketahui, grafiknya adalah gelombang sinus. Jika kosinus fungsi ini dikalikan dengan bilangan m tertentu, maka gelombang akan memuai dari sumbunya X(atau akan menyusut, tergantung nilai m).
Gelombang baru ini akan menjadi grafik fungsi y = mf(x), dimana m adalah bilangan real apa pun.
Jadi, fungsi y = mf(x) adalah fungsi familiar y = f(x) dikalikan dengan m.
JikaM< 1, то синусоида сжимается к оси X oleh koefisienM. Jikam > 1, maka sinusoidal tersebut diregangkan dari sumbunyaX oleh koefisienM.
Saat melakukan peregangan atau kompresi, pertama-tama Anda dapat memplot hanya satu setengah gelombang gelombang sinus, lalu menyelesaikan seluruh grafik.
Fungsikamu = F(kx).
Jika fungsinya kamu =mf(X) menyebabkan peregangan sinusoidal dari sumbu X atau kompresi terhadap sumbu X, maka fungsi y = f(kx) menyebabkan peregangan dari sumbu kamu atau kompresi terhadap sumbu kamu.
Selain itu, k adalah bilangan real apa pun.
Pada 0< k< 1 синусоида растягивается от оси kamu oleh koefisienk. Jikak > 1, maka sinusoidal tersebut tertekan menuju sumbukamu oleh koefisienk.
Saat membuat grafik fungsi ini, pertama-tama Anda dapat membuat setengah gelombang gelombang sinus, lalu menggunakannya untuk melengkapi keseluruhan grafik.
Fungsikamu = tgX.
Grafik fungsi kamu= tg X adalah garis singgung.
Cukup dengan membuat bagian grafik dalam interval dari 0 hingga π/2, dan kemudian Anda dapat melanjutkannya secara simetris dalam interval dari 0 hingga 3π/2.

Properti Fungsikamu = tgX:
Fungsikamu = ctgX
Grafik fungsi kamu=ctg X juga merupakan tangentoid (kadang-kadang disebut kotangentoid).

Properti Fungsikamu = ctgX:
Bagaimana cara membuat grafik fungsi y=sin x? Pertama, mari kita lihat grafik sinus pada interval tersebut.
Kami mengambil satu segmen sepanjang 2 sel di buku catatan. Pada sumbu Oy kami menandai satu.
Untuk memudahkan, kita membulatkan angka π/2 menjadi 1,5 (dan bukan menjadi 1,6, seperti yang disyaratkan oleh aturan pembulatan). Dalam hal ini, segmen dengan panjang π/2 setara dengan 3 sel.
Pada sumbu Ox kami menandai bukan segmen tunggal, tetapi segmen dengan panjang π/2 (setiap 3 sel). Oleh karena itu, segmen dengan panjang π sama dengan 6 sel, dan segmen dengan panjang π/6 sama dengan 1 sel.
Dengan pilihan segmen satuan ini, grafik yang digambarkan pada selembar buku catatan di dalam kotak sedapat mungkin sesuai dengan grafik fungsi y=sin x.
Mari kita buat tabel nilai sinus pada interval:
Kami menandai titik-titik yang dihasilkan pada bidang koordinat:

Karena y=sin x merupakan fungsi ganjil, grafik sinusnya simetris terhadap titik asal - titik O(0;0). Dengan mempertimbangkan fakta ini, mari kita lanjutkan menggambar grafik ke kiri, lalu titik -π:

Fungsi y=sin x periodik dengan periode T=2π. Oleh karena itu, grafik suatu fungsi yang diambil pada interval [-π;π] diulang berkali-kali ke kanan dan ke kiri.










 Mundur ke depan
Mundur ke depan
Perhatian! Pratinjau slide hanya untuk tujuan informasi dan mungkin tidak mewakili semua fitur presentasi. Jika Anda tertarik dengan karya ini, silakan unduh versi lengkapnya.
Besi berkarat tanpa ada gunanya,
Masih air membusuk atau membeku dalam cuaca dingin,
dan pikiran seseorang, karena tidak menemukan kegunaannya, merana.
Leonardo da Vinci
Teknologi yang digunakan: pembelajaran berbasis masalah, berpikir kritis, komunikasi komunikatif.
Sasaran:
- Pengembangan minat kognitif dalam belajar.
- Mempelajari sifat-sifat fungsi y = sin x.
- Pembentukan keterampilan praktis dalam membuat grafik fungsi y = sin x berdasarkan materi teori yang dipelajari.
Tugas:
1. Memanfaatkan potensi pengetahuan yang ada tentang sifat-sifat fungsi y = sin x dalam situasi tertentu.
2. Menerapkan pembentukan hubungan secara sadar antara model analitik dan geometri dari fungsi y = sin x.
Mengembangkan inisiatif, kemauan dan minat tertentu dalam mencari solusi; kemampuan untuk membuat keputusan, tidak berhenti di situ, dan mempertahankan sudut pandang Anda.
Menumbuhkan aktivitas kognitif siswa, rasa tanggung jawab, saling menghormati, saling pengertian, saling mendukung, dan percaya diri; budaya komunikasi.
Selama kelas
Tahap 1. Memperbarui pengetahuan dasar, memotivasi mempelajari materi baru
"Memasuki pelajaran."
Ada 3 pernyataan yang tertulis di papan tulis:
- Trigonometri persamaan dosa t = a selalu mempunyai solusi.
- Grafik fungsi ganjil dapat dibuat dengan menggunakan transformasi simetri terhadap sumbu Oy.
- Fungsi trigonometri dapat digambarkan dengan menggunakan satu setengah gelombang utama.
Siswa berdiskusi berpasangan: apakah pernyataan tersebut benar? (1 menit). Hasil pembahasan awal (ya, tidak) kemudian dimasukkan ke dalam tabel pada kolom “Sebelum”.
Guru menetapkan maksud dan tujuan pelajaran.
2. Memperbarui pengetahuan (secara frontal pada model lingkaran trigonometri).
Kita telah mengenal fungsi s = sin t.
1) Nilai apa yang dapat diambil oleh variabel t. Apa ruang lingkup fungsi ini?
2) Pada interval berapakah nilai ekspresi sin t terkandung? Tentukan nilai terbesar dan terkecil dari fungsi s = sin t.
3) Selesaikan persamaan sin t = 0.
4) Apa yang terjadi pada ordinat suatu titik ketika bergerak sepanjang seperempat pertama? (ordinatnya bertambah). Apa yang terjadi pada ordinat suatu titik ketika bergerak sepanjang kuarter kedua? (ordinatnya berangsur-angsur berkurang). Bagaimana hubungannya dengan monotonisitas fungsi? (fungsi s = sin t bertambah pada ruas dan berkurang pada ruas ).
5) Mari kita tuliskan fungsi s = sin t dalam bentuk y = sin x yang kita kenal (kita akan membangunnya dalam sistem koordinat xOy biasa) dan menyusun tabel nilai fungsi ini.
| X | 0 | ||||||
| pada | 0 | 1 | 0 |
Tahap 2. Persepsi, pemahaman, konsolidasi primer, hafalan yang tidak disengaja
Tahap 4. Sistematisasi utama pengetahuan dan metode kegiatan, transfer dan penerapannya dalam situasi baru
6. No.10.18 (b,c)
Tahap 5. Pengendalian akhir, koreksi, penilaian dan penilaian diri
7. Kita kembali ke pernyataan (awal pelajaran), berdiskusi menggunakan sifat-sifat fungsi trigonometri y = sin x, dan mengisi kolom “Sesudah” pada tabel.
8. D/z: ayat 10, No. 10.7(a), 10.8(b), 10.11(b), 10.16(a)
Berpusat pada satu titik A.
α
- sudut dinyatakan dalam radian.
Definisi
Sinus (dosa α)- Ini fungsi trigonometri, bergantung pada sudut α antara sisi miring dan kaki segitiga siku-siku, sama dengan perbandingan panjang kaki yang berhadapan |BC| dengan panjang sisi miring |AC|.
Kosinus (cos α) adalah fungsi trigonometri yang bergantung pada sudut α antara sisi miring dan kaki segitiga siku-siku, sama dengan perbandingan panjang kaki yang berdekatan |AB| dengan panjang sisi miring |AC|.
Notasi yang diterima
;
;
.
;
;
.
Grafik fungsi sinus y = sin x
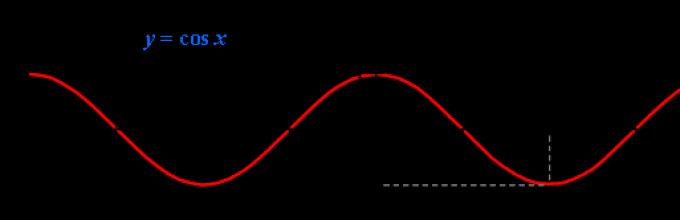
Grafik fungsi kosinus y = cos x

Sifat sinus dan cosinus
Periodisitas
Fungsi y = dosa x dan kamu = karena x periodik dengan periode 2π.
Keseimbangan
Fungsi sinusnya ganjil. Fungsi cosinusnya genap.
Domain definisi dan nilai, ekstrem, naik, turun
Fungsi sinus dan kosinus kontinu dalam domain definisinya, yaitu untuk semua x (lihat bukti kontinuitas). Properti utamanya disajikan dalam tabel (n - integer).
| kamu = dosa x | kamu = karena x | |
| Ruang lingkup dan kontinuitas | - ∞ < x < + ∞ | - ∞ < x < + ∞ |
| Jarak nilai | -1 ≤ kamu ≤ 1 | -1 ≤ kamu ≤ 1 |
| Meningkat | ||
| Menurun | ||
| Maksimum, y = 1 | ||
| Minimal, y = - 1 | ||
| Nol, y = 0 | ||
| Titik potong dengan sumbu ordinat, x = 0 | kamu = 0 | kamu = 1 |
Rumus dasar
Jumlah kuadrat sinus dan cosinus
Rumus sinus dan cosinus dari jumlah dan selisih
;
;
Rumus hasil kali sinus dan cosinus
Rumus jumlah dan selisih
Menyatakan sinus melalui kosinus
;
;
;
.
Menyatakan cosinus melalui sinus
;
;
;
.
Ekspresi melalui garis singgung
; .
Kapan kita punya:
;
.
Pada :
;
.
Tabel sinus dan cosinus, garis singgung dan kotangen
Tabel ini menunjukkan nilai sinus dan cosinus untuk nilai argumen tertentu. 
Ekspresi melalui variabel kompleks
;
rumus Euler
Ekspresi melalui fungsi hiperbolik
;
;
Derivatif
; . Menurunkan rumus > > >
Turunan dari orde ke-n:
{ -∞ <
x < +∞ }
Garis potong, garis potong
Fungsi terbalik
Fungsi terbalik sinus dan cosinus masing-masing adalah arcsinus dan arccosine.
Arcsinus, arcsin
Arccosine, arccos
Referensi:
DI DALAM. Bronstein, KA. Semendyaev, Buku Pegangan Matematika untuk Insinyur dan Mahasiswa, “Lan”, 2009.
Definisi geometris sinus dan kosinus
\(\sin \alpha = \dfrac(|BC|)(|AB|) \), \(\cos \alpha = \dfrac(|AC|)(|AB|) \)
α - sudut dinyatakan dalam radian.
Sinus (dosa α) adalah fungsi trigonometri sudut α antara sisi miring dan kaki segitiga siku-siku, sama dengan perbandingan panjang kaki dihadapannya |BC| dengan panjang sisi miring |AB|.
Kosinus (cos α) adalah fungsi trigonometri sudut α antara sisi miring dan kaki segitiga siku-siku, sama dengan perbandingan panjang kaki yang berdekatan |AC| dengan panjang sisi miring |AB|.
Definisi trigonometri
Dengan menggunakan rumus di atas, Anda dapat mencari sinus dan kosinus sudut lancip. Namun Anda perlu mempelajari cara menghitung sinus dan kosinus suatu sudut dengan ukuran berapa pun. Segitiga siku-siku tidak memberikan kesempatan ini ( sudut tumpul, misalnya, tidak boleh berada di dalamnya); oleh karena itu, diperlukan lebih banyak lagi definisi umum sinus dan kosinus, berisi rumus yang ditunjukkan sebagai kasus khusus.
Datang untuk menyelamatkan lingkaran trigonometri. Biarkan beberapa sudut diberikan; itu sesuai dengan titik dengan nama yang sama pada lingkaran trigonometri.
Beras. 2. Definisi trigonometri sinus dan kosinus
Kosinus suatu sudut adalah absis suatu titik. Sinus suatu sudut adalah ordinat suatu titik.
Pada Gambar. 2 sudutnya dianggap lancip, dan mudah untuk memahaminya definisi ini bertepatan dengan umum definisi geometris. Faktanya, kita melihat segitiga siku-siku dengan satuan sisi miring O dan sudut lancip. Kaki yang berdekatan dari segitiga ini adalah cos (bandingkan dengan Gambar 1) dan sekaligus absis titiknya; sisi yang berlawanan adalah sin (seperti pada Gambar 1) dan sekaligus ordinat titik.
Namun kini kami tidak lagi dibatasi oleh kuartal pertama dan memiliki peluang untuk memperluas definisi ini ke sudut mana pun. Pada Gambar. Gambar 3 menunjukkan berapa nilai sinus dan kosinus suatu sudut pada kuarter kedua, ketiga, dan keempat.

Beras. 3. Sinus dan kosinus pada triwulan II, III dan IV
Tabel nilai sinus dan cosinus
Sudut nol \(\LARGE 0^(\circ ) \)
Absis titik 0 sama dengan 1, ordinat titik 0 sama dengan 0. Karena itu,
cos 0 = 1 dosa 0 = 0

Gambar 4. Sudut nol
Sudut \(\BESAR \frac(\pi)(6) = 30^(\circ )\)
Kita melihat segitiga siku-siku dengan sisi miring satuan dan sudut lancip 30°. Seperti diketahui, kaki yang terletak berhadapan dengan sudut 30° sama dengan setengah sisi miring 1; dengan kata lain, kaki vertikal sama dengan 1/2 dan, oleh karena itu,
\[ \sin \frac(\pi)(6) =\frac(1)(2) \]
Kita mencari kaki horizontal menggunakan teorema Pythagoras (atau, yang sama, kita mencari kosinus menggunakan main identitas trigonometri):
\[ \cos \frac(\pi)(6) = \sqrt(1 - \kiri(\frac(1)(2) \kanan)^(2) ) =\frac(\sqrt(3) )(2 ) \]
1 Mengapa hal ini terjadi? Memotong segitiga sama sisi dengan sisi 2 sepanjang tingginya! Segitiga tersebut akan terbelah menjadi dua segitiga siku-siku dengan sisi miring 2, sudut lancip 30°, dan kaki yang lebih pendek 1.

Gambar 5. Sudut π/6
Sudut \(\BESAR \frac(\pi)(4) = 45^(\circ )\)
Dalam hal ini, segitiga siku-siku adalah sama kaki; Sinus dan kosinus sudut 45° sama besar. Mari kita nyatakan dengan x untuk saat ini. Kita punya:
\[ x^(2) + x^(2) = 1 \]
dari mana \(x=\frac(\sqrt(2) )(2) \). Karena itu,
\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Gambar 5. Sudut π/4
Sifat sinus dan cosinus
Notasi yang diterima
\(\sin^2 x \ekuivalen (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).
\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).
Periodisitas
Fungsi y = sin x dan y = cos x bersifat periodik dengan periode 2π.
\(\sin(x + 2\pi) = \sin x; \quad \)\(\cos(x + 2\pi) = \cos x \)
Keseimbangan
Fungsi sinusnya ganjil. Fungsi cosinusnya genap.
\(\sin(-x) = - \sin x; \kuad \)\(\cos(-x) = \cos x \)
Bidang definisi dan nilai, ekstrem, meningkat, menurun
Sifat dasar sinus dan cosinus disajikan pada tabel ( N- utuh).
| \(\kecil< x < \) | \(\kecil -\pi + 2\pi n \) \(\kecil< x < \) \(\small 2\pi n \) | |
| Menurun | \(\kecil \dfrac(\pi)2 + 2\pi n \)\(\kecil< x < \) \(\kecil \dfrac(3\pi)2 + 2\pi n \) | \(\kecil 2\pi n \) \(\kecil< x < \) \(\pi + \small 2\pi n \) |
| Maksimum, \(\kecil x = \) \(\kecil \dfrac(\pi)2 + 2\pi n \) | \(\x kecil = 2\pi n\) | |
| Minimal, \(\kecil x = \) \(\kecil -\dfrac(\pi)2 + 2\pi n \) | \(\kecil x = \) \(\kecil \pi + 2\pi n \) | |
| Nol, \(\small x = \pi n\) | \(\kecil x = \dfrac(\pi)2 + \pi n \) | |
| Titik potong sumbu Y, x = 0 | kamu = 0 | kamu = 1 |
Rumus dasar yang mengandung sinus dan cosinus
Jumlah kuadrat
\(\sin^2 x + \cos^2 x = 1\)
Rumus sinus dan cosinus untuk jumlah dan selisih
\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)
\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\kiri(\dfrac(\pi)2 - x \kanan) = \sin x \) ; \(\sin\kiri(\dfrac(\pi)2 - x \kanan) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)
Rumus hasil kali sinus dan cosinus
\(\sin x \cos y = \) \(\dfrac12 (\Besar [) \sin(x - y) + \sin(x + y) (\Besar ]) \)
\(\dosa x \dosa y = \) \(\dfrac12 (\Besar [) \cos(x - y) - \cos(x + y) (\Besar ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Besar [) \cos(x - y) + \cos(x + y) (\Besar ]) \)
\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Besar [) 1 - \cos 2x (\Besar ]) \)
\(\cos^2 x = \dfrac12 (\Besar [) 1 + \cos 2x (\Besar ]) \)
Rumus jumlah dan selisih
\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)
Menyatakan sinus melalui kosinus
\(\sin x = \cos\kiri(\dfrac(\pi)2 - x \kanan) = \)\(\cos\left(x - \dfrac(\pi)2 \kanan) = - \cos\left(x + \dfrac(\pi)2 \kanan) \)\(\sin^2 x = 1 - \cos^2 x \) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).
Menyatakan cosinus melalui sinus
\(\cos x = \sin\left(\dfrac(\pi)2 - x \kanan) = \)\(- \sin\kiri(x - \dfrac(\pi)2 \kanan) = \sin\kiri(x + \dfrac(\pi)2 \kanan) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).
Ekspresi melalui garis singgung
\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).
Pada \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).
Pada \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \)
:
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).
Tabel sinus dan cosinus, garis singgung dan kotangen
Tabel ini menunjukkan nilai sinus dan cosinus untuk nilai argumen tertentu.
[ img style="lebar-maks:500px;tinggi-maks:1080px;" src="tablitsa.png" alt="Tabel sinus dan cosinus" title="Tabel sinus dan cosinus" ]!}
Ekspresi melalui variabel kompleks
\(i^2 = -1\)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)
rumus Euler
\(e^(iz) = \cos z + i \sin z \)
Ekspresi melalui fungsi hiperbolik
\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)
Derivatif
\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Menurunkan rumus > > >
Turunan dari orde ke-n:
\(\kiri(\sin x \kanan)^((n)) = \sin\kiri(x + n\dfrac(\pi)2 \kanan) \)\(\kiri(\cos x \kanan)^((n)) = \cos\kiri(x + n\dfrac(\pi)2 \kanan) \).
Integral
\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Lihat juga bagian Tabel integral tak tentu >>>
Ekspansi seri
\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \)
!} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \)
!} \(\( - \infty< x < \infty \} \)
Garis potong, garis potong
\(\detik x = \dfrac1( \cos x ) ; \) \(\cosec x = \dfrac1( \sin x ) \)
Fungsi terbalik
Fungsi kebalikan dari sinus dan cosinus masing-masing adalah arcsinus dan arccosine.
Arcsinus, arcsin
\(y = \arcsin x\) \(\kiri\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \kanan\) \)
\(\sin(\arcsin x) = x\)
\(\arcsin(\sin x) = x\) \(\kiri\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \kanan\) \)
Arccosine, arccos
\(y = \arcos x\) \(\kiri\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \kanan\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x\) \(\( 0 \leqslant x \leqslant \pi \) \)
Referensi:
DI DALAM. Bronstein, KA. Semendyaev, Buku Pegangan Matematika untuk Insinyur dan Mahasiswa, “Lan”, 2009.
Untuk melakukan penghitungan, Anda harus mengaktifkan kontrol ActiveX!