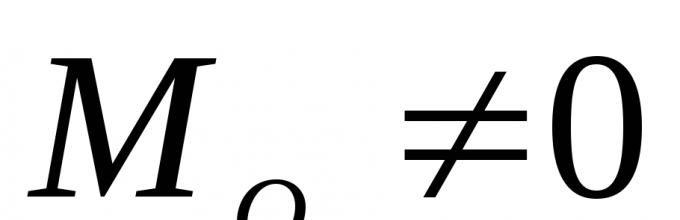Sistem datar dari gaya-gaya yang ditempatkan secara sewenang-wenang.

Kondisi keseimbangan pasangan gaya.

Jika suatu benda padat ditindaklanjuti oleh beberapa pasang gaya yang ditempatkan secara sembarang dalam ruang, maka dengan menerapkan aturan jajar genjang secara berurutan pada setiap dua momen pasangan gaya, sejumlah pasangan gaya dapat digantikan oleh satu pasangan gaya yang ekuivalen. , momennya sama dengan jumlah momen pasangan gaya tertentu.

Dalil. Untuk keseimbangan pasangan gaya yang diterapkan pada benda padat, jumlah aljabar proyeksi momen pasangan gaya pada masing-masing dari tiga sumbu koordinat harus sama dengan nol.

Mari kita perhatikan kasus perpindahan gaya ke suatu titik sembarang yang tidak terletak pada garis kerja gaya.

Mari kita ambil gaya F yang diterapkan di titik C. Kita perlu memindahkan gaya ini sejajar dengan dirinya sendiri ke titik tertentu O. Mari kita terapkan di titik O dua gaya F" dan F", berlawanan arah, sama besarnya dan sejajar dengan gaya yang diberikan. gaya F, yaitu F" = F" = F. Penerapan gaya-gaya ini di titik O tidak mengubah keadaan benda, karena keduanya seimbang. Sistem tiga gaya yang dihasilkan dapat dianggap terdiri dari gaya F" yang diterapkan di titik O, dan sepasang gaya FF" dengan momen M = Fa. Pasangan gaya ini disebut dianeksasi, dan lengannya a sama dengan lengan gaya F relatif terhadap titik O.

Jadi, ketika sebuah gaya F dibawa ke suatu titik yang tidak terletak pada garis kerja gaya tersebut, diperoleh sistem ekuivalen, yang terdiri dari sebuah gaya yang besar dan arahnya sama dengan gaya F, dan sepasang gaya yang terikat, momennya sama dengan momen gaya yang diberikan terhadap titik yang dilemparkan:

Sebagai contoh pengurangan gaya, perhatikan aksi gaya F pada ujung C batang yang dijepit (Gbr. 28, b). Setelah membawa gaya F ke titik O pada bagian yang dijepit, kita menemukan di dalamnya gaya F1 yang sama dan sejajar dengan gaya tertentu, dan momen terikat M sama dengan momen gaya yang diberikan F terhadap titik reduksi O,

1.4.2 Membawa sistem gaya bidang ke suatu titik tertentu

Metode yang dijelaskan untuk membawa satu gaya ke suatu titik tertentu dapat diterapkan pada sejumlah gaya berapa pun. Mari kita asumsikan bahwa gaya F1, F2, F3, F4 diterapkan pada titik-titik benda A, B, C dan D (Gbr. 30).

Gaya-gaya ini harus dibawa ke titik O pada bidang. Mari kita bayangkan terlebih dahulu gaya F1 yang bekerja di titik A. Mari kita terapkan di titik O dua gaya F1" dan F1"", sejajar dengannya dan arahnya berlawanan. Sebagai hasil dari gaya F1 yang dibawa, kita memperoleh gaya F1" yang diterapkan di titik O, dan sepasang gaya F1 "F1" dengan bahu a1. Dengan melakukan hal yang sama dengan gaya F2 yang diterapkan di titik B, kita mendapatkan gaya F2" yang diterapkan di titik O, dan sepasang gaya dengan bahu a2, dan seterusnya.

Kami mengganti sistem gaya datar yang diterapkan di titik A, B, C dan D dengan gaya konvergen F1, F2, F3, F4 yang diterapkan di titik O, dan pasangan gaya dengan momen yang sama dengan momen gaya-gaya tertentu relatif terhadap titik O :



Gaya-gaya yang konvergen pada suatu titik dapat digantikan dengan satu gaya F"hl yang sama dengan jumlah geometri komponen-komponennya,

Gaya yang sama dengan jumlah geometri gaya-gaya tertentu disebut vektor utama sistem gaya dan menunjukkan F"ch.

Berdasarkan aturan penjumlahan pasangan gaya, pasangan gaya tersebut dapat diganti dengan pasangan gaya yang dihasilkan, yang momennya sama dengan jumlah aljabar momen gaya-gaya tertentu terhadap titik O dan disebut Titik utama relatif terhadap titik referensi

Akibatnya, dalam kasus umum, sistem gaya datar akibat reduksi ke suatu titik O digantikan oleh sistem ekuivalen yang terdiri dari satu gaya (vektor utama) dan satu pasang (momen utama).

Perlu dipahami bahwa vektor utama F"ch adalah resultan dari sistem gaya tertentu, karena sistem ini tidak setara dengan satu gaya F"ch. Hanya dalam kasus khusus ketika momen utama lenyap maka vektor utama akan menjadi resultan sistem gaya-gaya tertentu. Karena vektor utama sama dengan jumlah geometri gaya-gaya suatu sistem tertentu, besaran maupun arahnya tidak bergantung pada pilihan pusat reduksi. Nilai dan tanda momen utama Mgl bergantung pada posisi pusat reduksi, karena lengan pasangan komponen bergantung pada posisi relatif gaya-gaya dan titik (pusat) relatif terhadap momen yang diambil.

Kasus-kasus penurunan sistem gaya berikut mungkin terjadi:
1. - kasus umum; sistem direduksi menjadi vektor utama dan momen utama.
2. ; sistem direduksi menjadi satu resultan yang sama dengan vektor utama sistem.
3. ; sistem direduksi menjadi sepasang gaya yang momennya sama dengan momen utama.
4. ; sistem berada dalam kesetimbangan, artinya, untuk kesetimbangan sistem gaya bidang, vektor utama dan momen utama harus sama dengan nol secara bersamaan.

Dapat dibuktikan bahwa pada keadaan umum, selalu ada suatu titik yang momen gaya utama sama dengan nol.

Mari kita perhatikan sistem bidang gaya yang dibawa ke titik O, yaitu digantikan oleh vektor utama yang diterapkan di titik O dan momen utama. Untuk lebih pastinya, kita asumsikan bahwa momen utama diarahkan searah jarum jam, yaitu . Mari kita nyatakan momen utama ini sebagai pasangan gaya FF", yang modulusnya akan dipilih sama dengan modulus vektor utama, yaitu. Kita akan menerapkan salah satu gaya yang membentuk pasangan di pusat reduksi O, gaya lain di titik C yang kedudukannya ditentukan dari syarat: Oleh karena itu .

Mari kita atur sepasang gaya sehingga gaya F"" diarahkan ke arah yang berlawanan dengan vektor utama F"ch. Di titik O kita mempunyai dua gaya yang sama besar dan berlawanan F"ch dan F"", diarahkan sepanjang garis lurus yang sama garis; mereka dapat dibuang (menurut aksioma ketiga). Oleh karena itu, relatif terhadap titik C, momen utama sistem gaya-gaya yang ditinjau sama dengan nol, dan sistem direduksi menjadi resultan.

Membawa sistem kekuatan ke pusat

Pertanyaan

Kuliah 6

3. Kondisi keseimbangan untuk sistem gaya yang sewenang-wenang

1. Pertimbangkan sistem gaya yang berubah-ubah. Mari kita pilih titik sembarang TENTANG di belakang pusat reduksi dan, dengan menggunakan teorema perpindahan gaya paralel, kita mentransfer semua gaya sistem ke titik tertentu, tidak lupa menambahkan pasangan gaya yang terkait saat mentransfer setiap gaya.

Mari kita gantikan sistem gaya-gaya konvergen yang dihasilkan dengan satu gaya yang sama dengan vektor utama sistem gaya-gaya aslinya. Sistem pasangan gaya yang terbentuk selama perpindahan akan digantikan oleh satu pasangan gaya yang momennya sama dengan jumlah geometri momen semua pasangan gaya (yaitu, jumlah geometri momen sistem gaya asal terhadap pusat TENTANG).

Momen ini disebut momen utama sistem gaya relatif terhadap pusat O (Gbr. 1.30).

Beras. 1.30. Membawa sistem kekuatan ke pusat

Jadi, sistem gaya apa pun selalu dapat digantikan hanya dengan dua faktor gaya - vektor utama dan momen utama relatif terhadap pusat reduksi yang dipilih secara sembarang . Jelasnya, vektor utama sistem gaya tidak bergantung pada pilihan pusat reduksi (vektor utama dikatakan invarian terhadap pilihan pusat reduksi). Jelas juga bahwa momen utama tidak memiliki sifat ini, sehingga selalu perlu untuk menunjukkan relatif terhadap pusat mana momen utama ditentukan.

2. Membawa sistem gaya ke bentuk yang paling sederhana

Kemungkinan penyederhanaan lebih lanjut dari sistem gaya sewenang-wenang bergantung pada nilai vektor utama dan momen utama, serta pada keberhasilan pemilihan pusat reduksi. Kasus-kasus berikut mungkin terjadi:

A) , . Dalam hal ini, sistem direduksi menjadi sepasang gaya dengan momen, yang besarnya tidak bergantung pada pilihan pusat reduksi.

B) , . Sistem direduksi menjadi resultan sama dengan , yang garis kerjanya melalui pusat TENTANG.

c) dan saling tegak lurus. Sistem direduksi menjadi resultan yang sama tetapi tidak melalui pusat TENTANG(Gbr. 1.31).

Beras. 1.31. Membawa sistem gaya ke resultan

Mari kita ganti momen utama dengan sepasang gaya, seperti ditunjukkan pada Gambar. 1.31. Mari kita definisikan R dari kondisi itu M 0 = R jam. Kemudian, berdasarkan aksioma statika yang kedua, mari kita tolak sistem seimbang antara dua gaya yang diterapkan pada suatu titik TENTANG.

d) dan paralel. Sistem ini digerakkan oleh sekrup dinamis, dengan sumbu melewati tengah TENTANG(Gbr. 1.32).

Beras. 1.32. Sekrup dinamis

e) dan tidak sama dengan nol, sekaligus vektor utama dan momen utama tidak sejajar dan tidak tegak lurus satu sama lain. Sistem digerakkan oleh sekrup dinamis, tetapi porosnya tidak melewati bagian tengah TENTANG(Gbr. 1.33).


Beras. 1.33. Kasus paling umum dalam mereduksi suatu sistem gaya

Mari kita asumsikan bahwa sistem gaya bidang sembarang direduksi menjadi satu gaya yang sama dengan vektor utama dan diterapkan pada pusat reduksi, dan menjadi sepasang gaya dengan momen yang sama dengan momen utama.
(Gambar 57, A). Mari kita buktikan bahwa sistem gaya bidang sembarang yang dipertimbangkan dalam kasus umum ini direduksi menjadi gaya resultan
, garis aksi yang melalui titik tersebut A, berjarak dari pusat reduksi yang dipilih TENTANG pada jarak
. Untuk melakukan ini, kami mengubah pasangan dengan momen
jadi kekuatan itu Dan
, yang membentuk pasangan ini, ternyata sama besarnya dengan vektor utama R". Dalam hal ini, perlu untuk memilih lengan pasangan sehingga momennya t
tetap sama dengan M 0. Untuk ini, leverage pasangan
seseorang jelas harus menemukan persamaannya

. (1)

Memanfaatkan fakta bahwa suatu pasangan selalu dapat dipindahkan dalam bidang aksinya sesuai keinginan, mari kita pindahkan pasangan tersebut
sehingga kekuatannya
menemukan dirinya melekat pada pusat adduksi TENTANG dan berlawanan dengan vektor utama
(Gambar 57, B).

Oleh karena itu, sistem gaya bidang sembarang yang dipertimbangkan setara dengan gaya
dan pasangan
. Mengembalikan kekuatan
Dan
sebagai seimbang, kita memperoleh bahwa seluruh sistem gaya yang dipertimbangkan digantikan oleh satu gaya
, yang karenanya merupakan resultan. Dalam hal ini, garis tindakan yang dihasilkan akan melewati titik tersebut A, yang posisinya relatif terhadap pusat reduksi yang dipilih ditentukan oleh rumus (1).

Jika, sebagai akibat dari membawa sistem gaya bidang sembarang, ternyata seperti ini
, A
, maka dalam kasus khusus ini sistem gaya-gaya ini segera digantikan oleh satu gaya, yaitu resultan
, garis aksi yang melewati pusat reduksi yang dipilih.

Masalah 7. Untuk poin DI DALAM Dan DENGAN benda masing-masing diterapkan gaya yang besarnya sama dan saling tegak lurus Dan
, jauh dari intinya TENTANG benda pada jarak yang sama
. Bawa sistem kekuatan ini ke titik tertentu TENTANG(Gambar 58).

Larutan. Mari kita transfer kekuatan Dan sejajar dengan diri kita sendiri ke suatu titik TENTANG. Sebagai hasil dari transfer ini kita memperoleh (Gambar 58) gaya
Dan
, diterapkan pada titik tersebut TENTANG, dan pasangan yang berdekatan
Dan
, berbaring di pesawat yang sama dengan momen
Dan
(gaya-gaya yang membentuk pasangan ini ditandai pada gambar dengan 58 garis). Dari penambahan gaya geometris Dan , diterapkan pada titik tersebut TENTANG, kita memperoleh vektor utama dari sistem gaya ini

yang modulusnya jelas sama dengan

Dari penjumlahan pasangan adjoint diperoleh pasangan resultan yang momennya sama dengan momen utama
sistem gaya tertentu relatif terhadap suatu titik TENTANG:

Oleh karena itu, sistem ini terdiri dari dua kekuatan Dan memiliki resultan

,

diterapkan pada titik tersebut A, yang jauh dari titik tersebut TENTANG pada jarak

.

;
,

yaitu bentuk-bentuk resultan dengan kedua gaya yang diberikan Dan sudut yang sama besar 45 0.

Tugas 8. Gaya vertikal bekerja pada rangka jembatan (Gambar 59)
t dan
t masing-masing pada jarak 10 M dan 40 M dari ujung kiri rangka dan gaya horizontal
t setinggi tali bagian atas rangka, tinggi rangka adalah 6 M. Bawalah sistem kekuatan ,Dan bentuk yang paling sederhana.

Larutan. Kita menggambar sumbu koordinat seperti yang ditunjukkan pada Gambar 59, dengan mengambil titik asal koordinat pada titik tersebut A. Mari kita cari proyeksi vektor utama suatu sistem gaya tertentu pada sumbu sistem koordinat yang dipilih:

di mana kita menemukan modul vektor utama
:

T
.

Sekarang mari kita cari momen utama dari sistem gaya-gaya tertentu relatif terhadap titik asal koordinat A:

tm
.

Oleh karena itu, sistem gaya ini mempunyai resultan
, modul siapa
T.

Sekarang mari kita cari garis aksi dari resultannya. Momen yang dihasilkan relatif terhadap asal usulnya A akan ditentukan oleh rumus

,

Di mana X Dan kamu - Koordinat suatu titik yang terletak pada garis aksi resultan. Karena
t dan
t, kalau begitu

.

DENGAN di sisi lain, dengan teorema Varignon pada momen resultan (5, § 11) kita punya

Karena itu,

.

Ini adalah persamaan garis aksi resultan.

Dengan asumsi dalam persamaan ini
, kita temukan titik potong garis aksi resultan dengan tali bagian atas rangka terletak agak jauh
M dari ujung kiri peternakan. Percaya
M, kita temukan titik potong garis aksi resultan dengan tali pengikat bagian bawah rangka berada pada jarak tertentu
M dari ujung kiri peternakan. Hubungan yang didefinisikan dengan cara ini adalah titik potong garis aksi resultan dengan tali busur atas dan bawah dalam satu garis lurus, kita cari garis kerja resultannya .

Mari kita gantikan sistem gaya datar yang diterapkan di titik A, B, C, D:

1) gaya F 1', F 2', F 3', F 4', diterapkan di titik O;

2) berpasangan gaya:

F 1 F 1': M 1 = M o (F 1) = F 1 a 1

F 2 F 2': M 2 = M o (F 2) = F 2 a 2

F 3 F 3' : M 3 ​​= M o (F 3) = F 3 a 3

F 4 F 4': M 4 = M o (F 4) = F 4 a 4

Gaya-gaya F 1', F 2', F 3', F 4' yang konvergen di titik O dapat digantikan oleh satu gaya (resultan) F ch:

F gl = F 1 ' + F 2 ' + F 3 ' + F 4 ' = F 1 + F 2 + F 3 + F 4

F bab– vektor utama sistem gaya.

Pasangan gaya yang dihasilkan dapat digantikan oleh pasangan gaya yang dihasilkan, yang momennya M ch:

M gl = M 1 + M 2 + M 3 + M 4 = Σ M i = Σ M o (F i)

M gl - poin utama mengenai titik referensi.

Sistem bidang gaya-gaya pada suatu titik O digantikan oleh sistem ekuivalen yang terdiri dari satu gaya (vektor utama) dan satu pasangan (momen utama).

Teorema momen resultan (teorema Varignon)

Momen sistem gaya-gaya bidang resultan terhadap suatu titik sembarang sama dengan jumlah aljabar momen-momen gaya-gaya komponen terhadap titik yang sama.

M o (F Σ)= Σ M o (F i)

Persamaan kesetimbangan sistem gaya bidang

FGL = 0;

M gl = ΣM o (F i) = 0.

Modulus vektor utama dapat ditentukan melalui proyeksi ke sumbu koordinat semua gaya sistem.

F GL = (ΣF іх) 2 +(ΣF іу) 2 =0 maka persamaan kesetimbangannya sebagai berikut:

Σ F х =0

Σ F у =0

Σ M o (F saya)=0

Bentuk persamaan kesetimbangan lainnya:

Σ M A (F saya)=0

Σ М В (F і)=0 (ABC tidak terletak pada bidang yang sama

Σ M C (F i)=0 langsung)

Σ M A (F i)=0 (sumbu x tidak tegak lurus

Σ M B (F і)=0 garis lurus AB)

Σ F х =0

Untuk sistem gaya paralel, dengan memilih salah satu sumbu proyeksi yang sejajar dengan gaya-gaya ini (sumbu y), dan sumbu lainnya tegak lurus (sumbu x), kita memperoleh dua persamaan kesetimbangan:

Σ F у =0

Σ M o (F saya)=0

Σ M A (F saya)=0

Σ MV (F i)=0

Algoritma untuk memecahkan masalah

1. Pilih objek keseimbangan (benda atau titik): kita akan mempertimbangkan keseimbangan relatif terhadap...

Kami menunjukkan pada gambar semua gaya yang bekerja, termasuk reaksi senyawa.

3. Pilih sistem koordinat - disarankan untuk mengarahkan sumbu koordinat sejajar atau tegak lurus terhadap gaya yang diperlukan.

Kami menyusun persamaan kesetimbangan untuk objek penelitian.

Σ F х =0

Σ F у =0

Σ M o (F saya)=0

Dari persamaan yang dihasilkan kita menentukan besaran yang tidak diketahui (kita menentukan reaksi).



Kami memeriksa kebenaran solusi persamaan.

Σ M p (F i)=0

Σ Saya (F saya)=0

5. Perangkat pendukung sistem balok

Mengartikulasikan dukungan

Bentuk tetap berengsel dan segel kaku (jepitan)

Subjek:

"Pusat gravitasi.

Karakteristik geometris bagian datar"

Rencana

1. Pusat gaya sejajar dan koordinatnya.
2. Pusat gravitasi suatu daerah. Momen statistik daerah.
3. Menyelesaikan masalah penentuan koordinat titik berat bangun datar komposit.
4. Momen inersia kutub dan aksial.
5. Momen inersia aksial terhadap sumbu sejajar.
6. Penentuan momen inersia penampang komposit menggunakan tabel bermacam-macam normal.

1. Pusat gaya paralel dan koordinatnya


Misalkan sistem gaya paralel F 1, F 2, F 3, ..., Fn diberikan; koordinat titik C 1, C2, C3, ..., Cn penerapan gaya-gaya ini diketahui (Gbr. 42, b). Mari kita nyatakan titik penerapannya dengan huruf resultan C, dan koordinatnya kita nyatakan x c, y c.
FΣ = F 1 + F 2 + F 3+…. + Fn = ΣF saya . (1)



FΣ xс = F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn = Σ F i x i ,

x c = F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / FΣ = Σ F i x i / FΣ

FΣ = F 1+ F 2+ F 3+…+ Fn= Σ F іх c =
= F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / F 1+ F 2+ F 3+…+ Fn= Σ F i x i / F i (2)

Metode yang dijelaskan untuk membawa satu gaya ke suatu titik tertentu dapat diterapkan pada sejumlah gaya berapa pun. Mari kita asumsikan hal itu pada titik-titik tubuh A,B,C Dan D(Gbr. 19) gaya yang diterapkan 1 , 2 , 3 Dan 4 . Hal ini diperlukan untuk membawa kekuatan-kekuatan ini ke titik sasaran TENTANG pesawat. Mari kita berikan kekuatan terlebih dahulu 1 , diterapkan pada titik tersebut A. Mari kita terapkan pada intinya TENTANG dua kekuatan ’ 1 Dan ’’ 1 , masing-masing modulusnya sama dengan gaya tertentu 1 , sejajar dengannya dan diarahkan ke arah yang berlawanan. Akibat membawa kekuatan 1 kita akan mendapatkan kekuatan ’ 1 , diterapkan pada titik tersebut TENTANG, dan beberapa kekuatan 1 ’’ 1 (gaya yang membentuk pasangan ditandai dengan garis putus-putus) dengan bahu sebuah 1. Dengan melakukan hal yang sama dengan paksa 2 , diterapkan pada titik tersebut DI DALAM, kita mendapatkan kekuatan 2 , diterapkan pada titik tersebut TENTANG, dan beberapa kekuatan 2 ’’ 2 dengan bahu sebuah 2 dll.

Sistem bidang gaya yang diterapkan pada titik-titik A, DI DALAM, DENGAN Dan D, kami menggantinya dengan gaya konvergen ’ 1 , ’ 2 , ’ 3 Dan ’ 4 , diterapkan pada titik tersebut TENTANG, dan pasangan gaya dengan momen yang sama dengan momen gaya-gaya tertentu terhadap titik tersebut TENTANG:

M 1 = P 1 a 1 = M o ( 1); M 2 = P 2 a 2 = M o (2);

M 3 = – P 3 a 3 = M o ( 3); M 4 = – P 4 a 4 = M o (4).

Gaya-gaya yang berkumpul pada suatu titik dapat digantikan oleh gaya tunggal " , sama dengan jumlah geometri komponen-komponennya,

" = " 1 + " 2 + " 3 + " 4 = 1 + 2 + 3 + 4 = saya .(16)

Gaya yang sama dengan jumlah geometri gaya-gaya tertentu disebut vektor utama sistem gaya.

Berdasarkan aturan penjumlahan pasangan gaya, dari dapat diganti dengan pasangan gaya yang dihasilkan, yang momennya sama dengan jumlah aljabar momen gaya-gaya tertentu terhadap titik tersebut. TENTANG:

M o = M 1 + M 2 + M 3 + M 4 = saya = o (saya).(17)

Dengan analogi vektor utama, momen M 0 pasangan yang sama dengan jumlah aljabar momen semua gaya relatif terhadap pusat reduksi TENTANG, ditelepon momen utama sistem relatif terhadap pusat reduksi tertentu O. Karena itu, dalam kasus umum, sistem gaya datar akibat reduksi ke titik tertentu O digantikan oleh sistem ekivalen yang terdiri dari satu gaya - vektor utama - dan satu pasangan, yang momennya disebut momen utama gaya sistem gaya tertentu relatif terhadap pusat reduksi.

Perlu dipahami bahwa vektor utama ’ bukanlah resultan dari suatu sistem gaya-gaya tertentu, karena sistem ini tidak setara dengan satu gaya ’. Hanya dalam kasus khusus ketika momen utama lenyap maka vektor utama akan menjadi resultan sistem gaya-gaya tertentu. Karena vektor utama sama dengan jumlah geometri gaya-gaya suatu sistem tertentu, besaran maupun arahnya tidak bergantung pada pilihan pusat reduksi. Besaran dan tanda momen utama M 0 bergantung pada posisi pusat reduksi, karena lengan pasangan komponen bergantung pada posisi relatif gaya-gaya dan titik (pusat) relatif terhadap pengambilan momen.

Kasus-kasus penurunan sistem gaya berikut mungkin terjadi:



1. " ≠ 0; M o ≠ 0 - kasus umum; sistem direduksi menjadi vektor utama dan momen utama.

2. " ≠ 0; M o = 0; sistem direduksi menjadi satu resultan yang sama dengan vektor utama sistem.

3. " = 0; M o ≠ 0; sistem direduksi menjadi sepasang gaya yang momennya sama dengan momen utama.

4. " = 0; M o = 0; sistem berada dalam keadaan setimbang.

Dapat dibuktikan bahwa secara umum kapan " ≠ 0 dan M o ≠ 0, Selalu ada titik dimana momen utama sistem gaya sama dengan nol.

Mari kita perhatikan suatu sistem bidang gaya-gaya yang direduksi menjadi suatu titik TENTANG, yaitu digantikan oleh vektor utama " ≠ 0 , diterapkan pada titik tersebut TENTANG, dan poin utama M o ≠ 0(Gbr. 20).

Untuk lebih jelasnya, kita asumsikan bahwa momen utama diarahkan searah jarum jam, yaitu. M o< 0. Mari kita gambarkan momen utama ini dengan sepasang kekuatan "" , modul yang dipilih sama dengan modul vektor utama " , yaitu R =R '' = R '. Salah satu gaya yang membentuk pasangan adalah gaya "" – berlaku di pusat reduksi TENTANG, kekuatan lain – pada titik tertentu DENGAN, yang kedudukannya ditentukan dari kondisi: M o = OS*R. Karena itu,

sistem operasi =. (18)

Mari kita mengerahkan beberapa kekuatan "" sehingga kekuatannya "" diarahkan ke arah yang berlawanan dengan vektor utama " . Pada intinya TENTANG(Gbr. 20) kita mempunyai dua gaya yang sama besar dan saling berlawanan " Dan "" , diarahkan sepanjang satu garis lurus; mereka dapat dibuang (menurut aksioma ketiga). Oleh karena itu, relatif terhadap intinya DENGAN momen utama sistem gaya-gaya yang ditinjau sama dengan nol, dan sistem direduksi menjadi resultan .

§ 18. Teorema momen resultan (teorema Varignon)

Dalam kasus umum (lihat § 17), sistem gaya bidang sembarang direduksi menjadi vektor utama " dan poin utama M 0 relatif terhadap pusat reduksi yang dipilih, dan momen utama sama dengan jumlah aljabar momen gaya-gaya tertentu relatif terhadap titik tersebut TENTANG

M o = o (saya).(A)

Ditunjukkan bahwa dimungkinkan untuk memilih pusat reduksi (pada Gambar 20 titik DENGAN), yang relatif terhadap momen utama sistem akan sama dengan nol, dan gaya-gaya sistem akan direduksi menjadi satu resultan yang besarnya sama dengan vektor utama ( R = R'). Mari kita tentukan momen resultan relatif terhadap titik tersebut TENTANG. Mengingat itu bahu sistem operasi kekuatan sama , kita mendapatkan

M o () = R*OC = R = M o.(B)

Dua besaran, yang secara terpisah sama dengan yang ketiga, adalah sama satu sama lain, oleh karena itu dari persamaan (a) dan (b) kita temukan

M o () = o ( saya).(19)

Persamaan yang dihasilkan mengungkapkan teorema Varignon: momen resultan sistem gaya-gaya bidang terhadap suatu titik sembarang sama dengan jumlah aljabar momen-momen gaya-gaya komponen terhadap titik yang sama.

Dari teorema Varignon dapat disimpulkan bahwa momen utama suatu sistem gaya bidang terhadap suatu titik yang terletak pada garis kerja resultannya sama dengan nol.