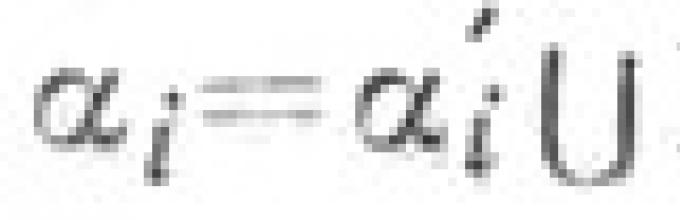Terdiri dari dua sinar berbeda yang memancar dari satu titik. Sinar disebut sisi U., dan permulaannya yang sama adalah bagian atas U. Misalkan [ VA),[Matahari) -
sisi sudut, DI DALAM - titik sudutnya adalah bidang yang dibatasi oleh sisi-sisi U. Gambar tersebut membagi bidang tersebut menjadi dua gambar ![]() i==l, 2, disebut juga U. atau sudut datar, disebut. wilayah bagian dalam datar U.
i==l, 2, disebut juga U. atau sudut datar, disebut. wilayah bagian dalam datar U.
Kedua sudut tersebut disebut sama (atau kongruen) jika keduanya dapat disejajarkan sehingga sisi dan simpul yang bersesuaian berhimpitan. Dari sinar mana pun pada suatu bidang, dalam arah tertentu darinya, dapat dibuat sumbu tunggal yang sama dengan sumbu tertentu.Perbandingan sumbu dilakukan dengan dua cara. Jika balok dianggap sebagai sepasang sinar yang mempunyai asal mula yang sama, maka untuk memperjelas pertanyaan mana di antara kedua balok yang lebih besar, perlu untuk menggabungkan simpul-simpul balok dan sepasang sisinya dalam satu bidang (lihat Gambar 1). Jika sisi kedua dari satu U. ternyata terletak di dalam U. yang lain, maka dikatakan bahwa U. pertama lebih kecil dari U. kedua. Cara kedua untuk membandingkan U. didasarkan pada perbandingan setiap U. dengan bilangan tertentu. U. yang sama akan sesuai dengan derajat yang sama atau (lihat di bawah), U yang lebih besar. - jumlah yang lebih besar, menjadi kurang - kurang.

Dua U. menelepon. bertetangga jika keduanya mempunyai titik sudut dan satu sisi yang sama, dan dua sisi lainnya membentuk garis lurus (lihat Gambar 2). Secara umum, U. yang mempunyai titik sudut yang sama dan satu sisi yang sama disebut. bersebelahan. kamu menelepon vertikal jika sisi-sisi yang satu merupakan perpanjangan melebihi bagian atas sisi-sisi yang lain.U vertikal sama satu sama lain. U yang sisi-sisinya membentuk garis lurus disebut. diperluas. Setengah dari U. yang diperluas disebut. lurus U. Langsung U. dapat didefinisikan secara ekuivalen secara berbeda: U. sama dengan yang berdekatan, disebut. langsung. Bagian dalam bidang datar, tidak melebihi bidang terbuka, merupakan daerah cembung pada bidang tersebut. Satuan ukuran U. diambil pecahan ke-90 dari garis U., disebut. derajat.

Apa yang disebut ukuran U. juga digunakan.Nilai numerik dari ukuran radian U. sama dengan panjang busur yang dipotong oleh sisi-sisi U. dari lingkaran satuan. Satu radian diberikan ke U yang sesuai dengan busur, yang sama dengan jari-jarinya. U. yang diperluas sama dengan radian.
Ketika dua garis lurus yang terletak pada bidang yang sama berpotongan dengan garis lurus ketiga, terbentuklah Us (lihat Gambar 3): 1 dan 5, 2 dan 6, 4 dan 8, 3 dan 7 - yang disebut. sesuai; 2 dan 5, 3 dan 8 - satu sisi internal; 1 dan 6, 4 dan 7 - satu sisi eksternal; 3 dan 5, 2 dan 8 - terletak di bagian dalam melintang; 1 dan 7, 4 dan 6 - berbaring melintang di luar.

Dalam praktek Dalam soal, disarankan untuk mempertimbangkan rotasi sebagai ukuran rotasi balok tetap di sekitar titik asal ke posisi tertentu. Tergantung pada arah putaran sinyal, dalam hal ini, sinyal positif dan negatif dapat dipertimbangkan. Jadi, U. dalam pengertian ini dapat memiliki nilai apa pun. Rotasi sinar dipertimbangkan dalam teori trigonometri. fungsi: untuk nilai argumen apa pun (U.), Anda dapat menentukan nilai trigonometri. fungsi. Konsep geometri dalam geometri. sistem, yang didasarkan pada aksiomatik titik-vektor, pada dasarnya berbeda dengan definisi U. sebagai gambar - dalam aksiomatik ini, U. dipahami sebagai metrik tertentu. besaran yang berhubungan dengan dua vektor dengan menggunakan operasi perkalian vektor skalar. Yaitu, setiap pasangan vektor a dan b menentukan sudut tertentu - suatu bilangan yang dihubungkan dengan vektor-vektor tersebut dengan rumus
![]()
Di mana ( a, b) -
produk skalar vektor.
Konsep U. sebagai bangun datar dan sebagai nilai numerik tertentu digunakan dalam berbagai geometri. masalah di mana U. ditentukan dengan cara khusus. Jadi, yang dimaksud dengan bentuk antara kurva-kurva yang berpotongan yang mempunyai garis singgung tertentu pada titik potongnya, yang dimaksud dengan bentuk yang dibentuk oleh garis singgung tersebut.
Sudut antara garis lurus dan bidang dianggap sudut yang dibentuk oleh garis lurus dan proyeksi persegi panjangnya pada bidang; itu diukur dalam kisaran dari 0
Ensiklopedia matematika. - M.: Ensiklopedia Soviet. I.M.Vinogradov. 1977-1985.
Sinonim:Lihat apa itu "SUDUT" di kamus lain:
bara- sudut / yok / ... Kamus ejaan morfemik
Suami. patah tulang, kekusutan, lutut, siku, tonjolan atau lipatan (depresi) pada satu sisi. Sudut linier, dua garis yang berlawanan dan jaraknya; bidang sudut atau bidang datar, pertemuan dua bidang atau dinding; sudutnya tebal, badan, bertemu menjadi satu... Kamus Dahl
Sudut, terhadap suatu sudut, pada (dalam) suatu sudut dan (mat.) dalam suatu sudut, m.1. Bagian bidang antara dua garis lurus yang berasal dari satu titik (mat.). Paling pojok. Sisi sudut. Mengukur sudut dalam derajat. Sudut kanan. (90°). Sudut tajam. (kurang dari 90°). Sudut tumpul.… … Kamus Penjelasan Ushakov
SUDUT- (1) sudut serang antara arah aliran udara yang mengalir ke sayap pesawat dan tali busur bagian sayap. Nilai gaya angkat bergantung pada sudut ini. Sudut dimana gaya angkat maksimum disebut sudut serang kritis. kamu... ... Ensiklopedia Politeknik Besar
- (datar) sosok geometris, dibentuk oleh dua sinar (sisi suatu sudut) yang muncul dari satu titik (titik sudut). Setiap sudut yang titik sudutnya berada di pusat lingkaran ( sudut tengah) mendefinisikan busur AB pada lingkaran yang dibatasi oleh titik... ... Kamus Ensiklopedis Besar
Kepala sudut, dari sekitar sudut, sudut bearish, sudut yang belum selesai, di semua sudut... Kamus sinonim dan ekspresi Rusia yang memiliki arti serupa. di bawah. ed. N. Abramova, M.: Kamus Rusia, 1999. sudut puncak, titik sudut; bantalan, tempat berlindung, deviatina, arah,... ... Kamus sinonim
sudut- sudut, batang. sudut; kalimat tentang batu bara, di (di) sudut dan dalam pidato para ahli matematika di bidang batu bara; hal. sudut, batang. sudut Dalam kombinasi preposisi dan stabil: di tikungan dan diperbolehkan untuk melewati tikungan (masuk, berbelok, dll.), dari sudut ke sudut (bergerak, posisi, dll.), sudut... ... Kamus kesulitan pengucapan dan stres dalam bahasa Rusia modern
SUDUT, pojok, di pojok, di (di) pojok, suami. 1. (di pojok.). Dalam geometri: sosok datar, dibentuk oleh dua sinar (dalam 3 nilai) yang memancar dari satu titik. Paling pojok. Langsung y. (90°). Akut kamu. (kurang dari 90°). Bodoh kamu. (lebih dari 90°). Eksternal dan internal...... Kamus Penjelasan Ozhegov
sudut- SUDUT, sudut, m Seperempat taruhan, ketika diumumkan, tepi kartu dilipat. ◘ As dan ratu sekop dengan sudut // Terbunuh. A.I.Polezhaev. Suatu hari di Moskow, 1832. ◘ Setelah makan malam, dia menyebarkan chervonet di atas meja, mengocok kartunya; penumpang memecahkan dek mereka... ... Terminologi dan jargon kartu abad ke-19
Definisi
Suatu bangun datar yang terdiri dari semua titik pada bidang yang dikelilingi oleh dua sinar yang memancar dari satu titik disebut sudut datar.
Definisi
Sudut antara dua berpotongan lurus adalah nilai sudut bidang terkecil pada perpotongan garis-garis tersebut. Jika dua garis sejajar, maka sudut antara keduanya dianggap nol.
Sudut antara dua garis yang berpotongan (jika sudut bidang diukur dalam radian) dapat bernilai dari nol hingga $\dfrac(\pi)(2)$.
Definisi
Sudut antara dua garis yang berpotongan adalah besaran yang sama dengan sudut antara dua garis yang berpotongan sejajar dengan garis yang berpotongan. Sudut antara garis $a$ dan $b$ dilambangkan dengan $\angle (a, b)$.
Kebenaran definisi yang diperkenalkan mengikuti teorema berikut.
Teorema sudut bidang yang sisi-sisinya sejajar
Besar dua sudut bidang cembung yang masing-masing sisinya sejajar dan berarah sama adalah sama.
Bukti
Jika sudut-sudutnya lurus, keduanya sama besar $\pi$. Jika tidak dibuka, maka kita plot segmen yang sama $ON=O_1ON_1$ dan $OM=O_1M_1$ pada sisi yang bersesuaian dari sudut $\angle AOB$ dan $\angle A_1O_1B_1$.
Segi empat $O_1N_1NO$ merupakan jajar genjang karena sisi-sisi yang berhadapan $ON$ dan $O_1N_1$ sama besar dan sejajar. Demikian pula segi empat $O_1M_1MO$ adalah jajar genjang. Oleh karena itu $NN_1 = OO_1 = MM_1$ dan $NN_1 \parallel OO_1 \parallel MM_1$, oleh karena itu, $NN_1=MM_1$ dan $NN_1 \parallel MM_1$ berdasarkan transitivitas. Segi empat $N_1M_1MN$ adalah jajar genjang, karena sisi-sisi yang berhadapan sama panjang dan sejajar. Artinya segmen $NM$ dan $N_1M_1$ adalah sama. Segitiga $ONM$ dan $O_1N_1M_1$ adalah sama menurut kriteria ketiga persamaan segitiga, yang artinya sudut yang sesuai$\angle NOM$ dan $\angle N_1O_1M_1$ sama.
Misalkan dua vektor bukan nol diberikan pada suatu bidang atau ruang tiga dimensi. Mari kita tunda dari titik yang sewenang-wenang HAI vektor dan . Maka definisi berikut ini valid.
Definisi.
Sudut antar vektor dan sudut antar sinar disebut O.A. Dan O.B..
Sudut antara vektor dan akan dilambangkan sebagai .
Sudut antar vektor dapat diambil nilainya 0 ke atau, yang merupakan hal yang sama, dari ke.
Jika kedua vektor mempunyai arah yang sama, maka vektor-vektor tersebut juga mempunyai arah yang berlawanan.
Definisi.
Vektor disebut tegak lurus, jika sudut antara keduanya sama dengan (radian).
Jika paling sedikit salah satu vektornya nol, maka sudutnya tidak terdefinisi.
Mencari sudut antar vektor, contoh dan penyelesaiannya.
Kosinus sudut antara vektor dan , dan karenanya sudut itu sendiri, secara umum dapat ditemukan menggunakan produk skalar vektor, atau menggunakan teorema kosinus untuk segitiga yang dibangun di atas vektor dan .
Mari kita lihat kasus-kasus ini.
Menurut definisi, hasil kali skalar vektor adalah . Jika vektor dan bukan nol, maka kita dapat membagi kedua ruas persamaan terakhir dengan hasil kali panjang vektor dan , dan kita peroleh rumus mencari kosinus sudut antara vektor bukan nol: . Rumus ini dapat digunakan jika panjang vektor dan hasil kali skalarnya diketahui.
Contoh.
Hitung kosinus sudut antara vektor dan , dan cari juga sudutnya sendiri jika panjang vektor dan sama 3 Dan 6 masing-masing, dan produk skalarnya sama dengan -9 .
Larutan.
Pernyataan masalah berisi semua besaran yang diperlukan untuk menerapkan rumus. Kami menghitung kosinus sudut antara vektor dan: .
Sekarang kita mencari sudut antar vektor: .
Menjawab:
Terdapat permasalahan dimana vektor ditentukan oleh koordinat dalam sistem koordinat persegi panjang pada bidang atau ruang. Dalam kasus ini, untuk mencari kosinus sudut antar vektor, Anda dapat menggunakan rumus yang sama, tetapi dalam bentuk koordinat. Ayo kita mulai.
Panjang suatu vektor adalah akar kuadrat dari jumlah kuadrat koordinatnya, hasil kali skalar vektor sama dengan jumlah hasil kali koordinat-koordinat yang bersesuaian. Karena itu, rumus menghitung kosinus sudut antar vektor pada bidang mempunyai bentuk , dan untuk vektor dalam ruang tiga dimensi - .
Contoh.
Temukan sudut antara vektor yang diberikan dalam sistem koordinat persegi panjang.
Larutan.
Anda bisa langsung menggunakan rumus:
Atau Anda bisa menggunakan rumus untuk mencari kosinus sudut antar vektor, setelah sebelumnya menghitung panjang vektor dan hasil kali skalar pada koordinat:
Menjawab:
Masalahnya direduksi menjadi kasus sebelumnya ketika koordinat tiga titik diberikan (misalnya A, DI DALAM Dan DENGAN) dalam sistem koordinat persegi panjang dan Anda perlu mencari sudut tertentu (misalnya, ).
Memang sudutnya sama dengan sudut antara vektor dan . Koordinat vektor-vektor ini dihitung sebagai perbedaan antara koordinat titik akhir dan titik awal vektor yang bersesuaian.
Contoh.
Pada bidang datar, koordinat tiga titik diberikan dalam sistem koordinat Kartesius. Temukan kosinus sudut antara vektor dan .
Larutan.
Mari kita tentukan koordinat vektor dan koordinat titik-titik yang diberikan:
Sekarang mari kita gunakan rumus untuk mencari kosinus sudut antar vektor pada bidang dalam koordinat:
Menjawab:
Sudut antara vektor dan juga dapat dihitung dengan teorema kosinus. Jika kita menunda dari pokok permasalahannya HAI vektor dan , kemudian dengan teorema kosinus dalam segitiga OAV kita dapat menulis, yang setara dengan persamaan, dari mana kita menemukan kosinus sudut antara vektor. Untuk menerapkan rumus yang dihasilkan, kita hanya memerlukan panjang vektor dan , yang dapat dengan mudah dicari dari koordinat vektor dan . Namun cara ini praktis tidak digunakan, karena kosinus sudut antar vektor lebih mudah dicari dengan menggunakan rumus.
Perhitungan proyeksi ortogonal(proyeksi sendiri):
Proyeksi vektor ke sumbu l sama dengan produk modulus vektor dan kosinus sudut φ antara vektor dan sumbu, yaitu. pr cosφ.
Dok: Jika φ=< , то пр l =+ = *cos φ.
Jika φ> (φ≤ ), maka pr l =- =- * cos( -φ) = cosφ (lihat Gambar 10)
Jika φ= , maka pr l = 0 = cos φ.
Konsekuensi: Proyeksi suatu vektor pada suatu sumbu adalah positif (negatif) jika vektor tersebut membentuk sudut lancip (tumpul) dengan sumbunya, dan sama dengan nol jika sudut tersebut siku-siku.
Konsekuensi: Proyeksi vektor-vektor yang sama besar pada sumbu yang sama adalah sama besar satu sama lain.
Perhitungan proyeksi ortogonal jumlah vektor (properti proyeksi):
Proyeksi jumlah beberapa vektor pada sumbu yang sama sama dengan jumlah proyeksinya pada sumbu tersebut.
Dok: Misal = + + . Kita mempunyai pr l =+ =+ + - , yaitu. pr l (+ + ) = pr l + pr l + pr l (lihat Gambar 11)
BERAS. sebelas
Perhitungan hasil kali vektor dan bilangan:
Jika suatu vektor dikalikan dengan suatu bilangan λ, maka proyeksinya terhadap sumbu juga dikalikan dengan bilangan tersebut, yaitu. pr aku (λ* )= λ* pr aku .
Bukti: Untuk λ > 0 kita mempunyai pr l (λ* )= *cos φ = λ* φ = λ*pr l
Ketika λl (λ* )= *cos( -φ)=- * (-cosφ) = * cosφ= λ *pr l .
Properti ini juga berlaku ketika
Jadi, operasi linier pada vektor menghasilkan operasi yang bersesuaian operasi linier atas proyeksi vektor-vektor ini.
Materi ini dikhususkan untuk konsep sudut antara dua garis yang berpotongan. Di paragraf pertama kami akan menjelaskan apa itu dan menunjukkannya dalam ilustrasi. Kemudian kita akan melihat cara di mana Anda dapat menemukan sinus, kosinus dari sudut ini dan sudut itu sendiri (kami akan mempertimbangkan secara terpisah kasus dengan bidang dan ruang tiga dimensi), kami akan memberikan rumus yang diperlukan dan menunjukkan dengan tepat dengan contoh bagaimana mereka digunakan dalam praktik.
Untuk memahami besarnya sudut yang terbentuk pada perpotongan dua garis, kita perlu mengingat pengertian sudut, tegak lurus, dan titik potong.
Definisi 1
Kita menyebut dua garis berpotongan jika keduanya mempunyai satu poin umum. Titik ini disebut titik potong dua garis.
Setiap garis lurus dibagi oleh titik potong menjadi sinar-sinar. Kedua garis lurus tersebut membentuk 4 sudut, dua diantaranya vertikal dan dua lagi berdekatan. Jika kita mengetahui ukuran salah satunya, maka kita dapat menentukan sisanya.
Katakanlah kita mengetahui bahwa salah satu sudutnya sama dengan α. Dalam hal ini, sudut vertikal terhadapnya juga akan sama dengan α. Untuk mencari sudut yang tersisa, kita perlu menghitung selisih 180° - . Jika α sama dengan 90 derajat, maka semua sudut siku-siku. Garis yang berpotongan tegak lurus disebut tegak lurus (artikel terpisah dikhususkan untuk konsep tegak lurus).
Lihatlah gambar:
Mari kita beralih ke merumuskan definisi utama.
Definisi 2
Sudut yang dibentuk oleh dua garis yang berpotongan adalah besar sudut yang lebih kecil dari 4 sudut yang membentuk kedua garis tersebut.
Kesimpulan penting harus diambil dari definisi tersebut: besar sudut dalam hal ini akan dinyatakan dengan sembarang bilangan real dalam interval (0, 90]. Jika garis-garisnya tegak lurus, maka sudut di antara keduanya akan sama dengan 90 derajat.

Kemampuan untuk menemukan ukuran sudut antara dua garis yang berpotongan berguna untuk menyelesaikan banyak hal masalah praktis. Metode penyelesaiannya dapat dipilih dari beberapa pilihan.
Untuk memulainya, kita dapat mengambil metode geometris. Jika kita mengetahui sesuatu tentang sudut-sudut yang saling melengkapi, maka kita dapat menghubungkannya dengan sudut yang kita perlukan dengan menggunakan sifat-sifat bangun datar yang sama besar atau sebangun. Misalnya, jika kita mengetahui sisi-sisi suatu segitiga dan perlu menghitung sudut antara garis-garis di mana sisi-sisi tersebut berada, maka teorema kosinus cocok untuk penyelesaian kita. Jika kita mempunyai syaratnya segitiga siku-siku, maka untuk perhitungannya kita juga membutuhkan pengetahuan tentang sinus, cosinus dan tangen suatu sudut.
Metode koordinat juga sangat cocok untuk memecahkan masalah jenis ini. Mari kami jelaskan cara menggunakannya dengan benar.
Kita mempunyai sistem koordinat persegi panjang (Kartesius) O x y, yang di dalamnya diberikan dua garis lurus. Mari kita nyatakan dengan huruf a dan b. Garis lurus dapat dijelaskan dengan menggunakan beberapa persamaan. Garis asal mempunyai titik potong M. Bagaimana cara menentukan sudut yang diperlukan (sebut saja α) antara garis lurus ini?
Mari kita mulai dengan merumuskan prinsip dasar mencari sudut dalam kondisi tertentu.
Kita mengetahui bahwa konsep garis lurus erat kaitannya dengan konsep vektor arah dan vektor normal. Jika kita mempunyai persamaan garis tertentu, kita dapat mengambil koordinat vektor-vektor tersebut dari persamaan tersebut. Kita dapat melakukan ini untuk dua garis yang berpotongan sekaligus.
Sudut yang dibentuk oleh dua garis yang berpotongan dapat dicari dengan menggunakan:
- sudut antar vektor arah;
- sudut antara vektor normal;
- sudut antara vektor normal suatu garis dan vektor arah garis lainnya.
Sekarang mari kita lihat setiap metode secara terpisah.
1. Misalkan kita mempunyai garis a dengan vektor arah a → = (ax, a y) dan garis b dengan vektor arah b → (b x, b y). Sekarang mari kita gambarkan dua vektor a → dan b → dari titik potong. Setelah ini kita akan melihat bahwa masing-masingnya akan ditempatkan pada garis lurusnya masing-masing. Lalu kami memiliki empat opsi untuk mereka posisi relatif. Lihat ilustrasi:

Jika sudut antara dua vektor tidak tumpul, maka itulah sudut yang kita perlukan antara perpotongan garis a dan b. Jika tumpul, maka sudut yang diinginkan sama dengan sudut yang berdekatan dengan sudut a →, b → ^. Jadi, α = a → , b → ^ jika a → , b → ^ ≤ 90 ° , dan α = 180 ° - a → , b → ^ jika a → , b → ^ > 90 ° .
Berdasarkan fakta bahwa cosinus sudut yang sama sama, kita dapat menulis ulang persamaan yang dihasilkan sebagai berikut: cos α = cos a → , b → ^ , jika a → , b → ^ ≤ 90 ° ; cos α = cos 180° - a →, b → ^ = - cos a →, b → ^, jika a →, b → ^ > 90°.
Dalam kasus kedua, rumus reduksi digunakan. Dengan demikian,
cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^
Mari kita tulis rumus terakhir dengan kata-kata:
Definisi 3
Kosinus sudut yang dibentuk oleh dua garis lurus yang berpotongan sama dengan modulus kosinus sudut antara vektor arahnya.
Bentuk umum rumus kosinus sudut antara dua vektor a → = (a x , a y) dan b → = (b x , b y) terlihat seperti ini:
cos a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Dari situ kita dapat memperoleh rumus kosinus sudut antara dua garis lurus tertentu:
cos α = a x b x + a y + b ya a x 2 + a y 2 b x 2 + b y 2 = a x b x + a y + b ya a x 2 + a y 2 b x 2 + b y 2
Maka sudutnya sendiri dapat dicari dengan menggunakan rumus berikut:
α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Di sini a → = (ax , a y) dan b → = (b x , b y) adalah vektor arah dari garis-garis tertentu.
Mari kita beri contoh penyelesaian masalah.
Contoh 1
Dalam sistem koordinat persegi panjang pada suatu bidang, diberikan dua garis berpotongan a dan b. Mereka dapat dijelaskan dengan persamaan parametrik x = 1 + 4 · λ y = 2 + λ λ ∈ R dan x 5 = y - 6 - 3. Hitung sudut antara garis-garis ini.
Larutan
Kami memiliki kondisi kami persamaan parametrik, artinya untuk garis ini kita dapat langsung menuliskan koordinat vektor arahnya. Untuk melakukan ini, kita perlu mengambil nilai koefisien untuk parameternya, mis. garis lurus x = 1 + 4 · λ y = 2 + λ λ ∈ R mempunyai vektor arah a → = (4, 1).
Garis lurus kedua dijelaskan menggunakan persamaan kanonik x 5 = kamu - 6 - 3 . Di sini kita dapat mengambil koordinat dari penyebutnya. Jadi, garis ini mempunyai vektor arah b → = (5 , - 3) .
Selanjutnya kita langsung mencari sudutnya. Caranya, cukup substitusikan koordinat kedua vektor yang ada ke dalam rumus di atas α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2 . Kami mendapatkan yang berikut:
α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45°
Menjawab: Garis lurus ini membentuk sudut 45 derajat.
Kita dapat menyelesaikan masalah serupa dengan mencari sudut antara vektor normal. Jika kita mempunyai garis a dengan vektor normal n a → = (n a x , n a y) dan garis b dengan vektor normal n b → = (n b x , n b y), maka sudut antara keduanya sama dengan sudut antara n a → dan n b → atau sudut yang berdekatan dengan n a →, n b → ^. Cara ini ditunjukkan pada gambar:

Rumus untuk menghitung kosinus sudut antara garis berpotongan dan sudut itu sendiri menggunakan koordinat vektor normal adalah sebagai berikut:
cos α = cos n a → , n b → ^ = n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2 α = a r c cos n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2
Di sini n a → dan n b → menyatakan vektor normal dari dua garis tertentu.
Contoh 2
Dalam sistem koordinat persegi panjang, dua garis lurus diberikan dengan menggunakan persamaan 3 x + 5 y - 30 = 0 dan x + 4 y - 17 = 0. Temukan sinus dan kosinus sudut di antara keduanya dan besar sudut itu sendiri.
Larutan
Garis asli ditentukan menggunakan persamaan biasa garis lurus berbentuk A x + B y + C = 0. Kami menyatakan vektor normal sebagai n → = (A, B). Mari kita cari koordinat vektor normal pertama untuk satu garis dan tuliskan: n a → = (3, 5) . Untuk baris kedua x + 4 y - 17 = 0, vektor normalnya mempunyai koordinat n b → = (1, 4). Sekarang mari tambahkan nilai yang diperoleh ke rumus dan hitung totalnya:
cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34
Jika kita mengetahui cosinus suatu sudut, maka kita dapat menghitung sinusnya menggunakan dasar identitas trigonometri. Karena sudut α yang dibentuk oleh garis lurus tidak tumpul, maka sin α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.
Dalam hal ini, α = a r c cos 23 2 34 = a r c sin 7 2 34.
Jawaban: cos α = 23 2 34, sin α = 7 2 34, α = a r c cos 23 2 34 = a r c sin 7 2 34
Mari kita analisis kasus terakhir - mencari sudut antara garis lurus jika kita mengetahui koordinat vektor arah suatu garis lurus dan vektor normal garis lainnya.
Misalkan garis lurus a mempunyai vektor arah a → = (ax , a y) , dan garis lurus b mempunyai vektor normal n b → = (n b x , n b y) . Kita perlu mengesampingkan vektor-vektor ini dari titik perpotongannya dan mempertimbangkan semua opsi untuk posisi relatifnya. Lihat di gambar:

Jika sudut antara vektor-vektor tertentu tidak lebih dari 90 derajat, ternyata sudut antara a dan b akan membentuk sudut siku-siku.
a → , n b → ^ = 90 ° - α jika a → , n b → ^ ≤ 90 ° .
Jika kurang dari 90 derajat, maka diperoleh hasil sebagai berikut:
a → , n b → ^ > 90 ° , maka a → , n b → ^ = 90 ° + α
Dengan menggunakan aturan persamaan kosinus sudut yang sama, kita menulis:
cos a → , n b → ^ = cos (90 ° - α) = sin α untuk a → , n b → ^ ≤ 90 ° .
cos a → , n b → ^ = cos 90 ° + α = - sin α untuk a → , n b → ^ > 90 ° .
Dengan demikian,
sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^ , a → , n b → ^ > 0 - cos a → , n b → ^ , a → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^
Mari kita merumuskan kesimpulan.
Definisi 4
Untuk mencari sinus sudut antara dua garis yang berpotongan pada suatu bidang, Anda perlu menghitung modulus kosinus sudut antara vektor arah garis pertama dan vektor normal garis kedua.
Mari kita tuliskan rumus yang diperlukan. Mencari sinus suatu sudut:
sin α = cos a → , n b → ^ = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Menemukan sudut itu sendiri:
α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Di sini a → adalah vektor arah garis pertama, dan n b → adalah vektor normal garis kedua.
Contoh 3
Dua garis berpotongan diberikan oleh persamaan x - 5 = y - 6 3 dan x + 4 y - 17 = 0. Temukan sudut persimpangan.
Larutan
Kami mengambil koordinat panduan dan vektor normal dari persamaan yang diberikan. Ternyata a → = (- 5, 3) dan n → b = (1, 4). Kita ambil rumus α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 dan hitung:
α = a r c sin = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sin 7 2 34
Harap dicatat bahwa kami mengambil persamaan dari soal sebelumnya dan memperoleh hasil yang persis sama, tetapi dengan cara yang berbeda.
Menjawab:α = a r c sin 7 2 34
Mari kita tunjukkan cara lain untuk mencari sudut yang diinginkan menggunakan koefisien sudut garis lurus tertentu.
Kita mempunyai garis a, yang didefinisikan dalam sistem koordinat persegi panjang menggunakan persamaan y = k 1 x + b 1, dan garis b, yang didefinisikan sebagai y = k 2 x + b 2. Ini adalah persamaan garis dengan kemiringan. Untuk mencari sudut potong, kita menggunakan rumus:
α = a r c cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, dimana k 1 dan k 2 adalah gradien dari garis-garis yang diberikan. Untuk memperoleh notasi tersebut digunakan rumus penentuan sudut melalui koordinat vektor normal.
Contoh 4
Ada dua garis yang berpotongan pada suatu bidang, diberikan oleh persamaan y = - 3 5 x + 6 dan y = - 1 4 x + 17 4. Hitung nilai sudut potongnya.
Larutan
Koefisien sudut garis kita sama dengan k 1 = - 3 5 dan k 2 = - 1 4. Mari kita tambahkan ke rumus α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 dan hitung:
α = a r c cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = a r c cos 23 20 34 24 · 17 16 = a r c cos 23 2 34
Menjawab:α = a r c cos 23 2 34
Dalam kesimpulan paragraf ini, perlu diperhatikan bahwa rumus mencari sudut yang diberikan di sini tidak harus dihafal. Untuk melakukan ini, cukup mengetahui koordinat pemandu dan/atau vektor normal garis tertentu dan dapat menentukannya dengan jenis yang berbeda persamaan. Namun ada baiknya mengingat atau menuliskan rumus menghitung kosinus suatu sudut.
Cara menghitung sudut antar garis yang berpotongan dalam ruang
Perhitungan sudut tersebut dapat direduksi menjadi menghitung koordinat vektor-vektor arah dan menentukan besarnya sudut yang dibentuk oleh vektor-vektor tersebut. Untuk contoh seperti itu, alasan yang sama yang kami berikan sebelumnya digunakan.
Misalkan kita mempunyai sistem koordinat persegi panjang yang terletak pada ruang tiga dimensi. Ini berisi dua garis lurus a dan b dengan titik potong M. Untuk menghitung koordinat vektor arah, kita perlu mengetahui persamaan garis-garis tersebut. Mari kita nyatakan vektor arah a → = (a x , a y , a z) dan b → = (b x , b y , b z) . Untuk menghitung kosinus sudut di antara keduanya, kita menggunakan rumus:
cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Untuk mencari sudutnya sendiri, kita membutuhkan rumus berikut:
α = a r c cos a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Contoh 5
Kita mempunyai garis yang didefinisikan dalam ruang tiga dimensi menggunakan persamaan x 1 = y - 3 = z + 3 - 2. Diketahui berpotongan dengan sumbu O z. Hitung sudut potong dan kosinus sudut tersebut.
Larutan
Mari kita nyatakan sudut yang perlu dihitung dengan huruf α. Mari kita tuliskan koordinat vektor arah garis lurus pertama – a → = (1, - 3, - 2) . Untuk aplikasi axis bisa kita ambil koordinat vektor k → = (0, 0, 1) sebagai panduan. Kami telah menerima data yang diperlukan dan dapat menambahkannya ke rumus yang diinginkan:
cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2
Hasilnya, kami menemukan bahwa sudut yang kami butuhkan sama dengan a r c cos 1 2 = 45 °.
Menjawab: karena α = 1 2 , α = 45° .
Jika Anda melihat kesalahan pada teks, silakan sorot dan tekan Ctrl+Enter