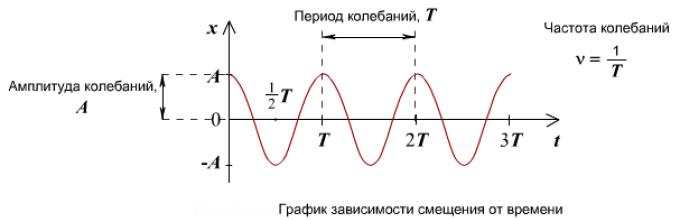
Persamaan getaran harmonik
Persamaan osilasi harmonik menetapkan ketergantungan koordinat benda terhadap waktu


Grafik kosinus pada momen awal bernilai maksimum, dan grafik sinus bernilai nol pada momen awal. Jika kita mulai mengamati osilasi dari posisi setimbang, maka osilasi akan berulang secara sinusoidal. Jika kita mulai memperhatikan osilasi dari posisi deviasi maksimum, maka osilasi akan digambarkan dengan kosinus. Atau osilasi seperti itu dapat dijelaskan dengan rumus sinus dengan fase awal.
Perubahan kecepatan dan percepatan selama osilasi harmonik
Tidak hanya koordinat benda yang berubah seiring waktu menurut hukum sinus atau kosinus. Namun besaran seperti gaya, kecepatan dan percepatan juga berubah dengan cara yang sama. Gaya dan percepatan maksimum bila benda yang berosilasi berada pada posisi ekstrim dimana perpindahan maksimum, dan bernilai nol bila benda melewati posisi setimbang. Sebaliknya, kecepatan pada posisi ekstrim adalah nol, dan ketika benda melewati posisi setimbang, ia mencapai nilai maksimumnya.
Jika osilasi dijelaskan oleh hukum kosinus


Jika osilasi dijelaskan menurut hukum sinus


Nilai kecepatan dan percepatan maksimum
Setelah menganalisis persamaan ketergantungan v(t) dan a(t), kita dapat menebak bahwa nilai maksimum kecepatan dan percepatan terjadi pada kasus ketika faktor trigonometri sama dengan 1 atau -1. Ditentukan oleh rumus
§ 6. GETARAN MEKANIKRumus dasar
Persamaan Harmonik
Di mana X - perpindahan titik osilasi dari posisi setimbang; T- waktu; A,ω, φ - masing-masing amplitudo, frekuensi sudut, fase awal osilasi; - fase osilasi saat ini T.
Frekuensi sudut
dimana ν dan T adalah frekuensi dan periode osilasi.
Kecepatan suatu titik yang melakukan osilasi harmonik adalah
Percepatan pada osilasi harmonik
Amplitudo A osilasi yang dihasilkan, diperoleh dengan menjumlahkan dua osilasi dengan frekuensi yang sama, yang terjadi sepanjang satu garis lurus, ditentukan dengan rumus
Di mana A 1 Dan A 2 - amplitudo komponen getaran; φ 1 dan φ 2 adalah fase awalnya.
Fase awal φ dari osilasi yang dihasilkan dapat ditemukan dari rumus
![]()
Frekuensi denyut yang timbul bila dijumlahkan dua getaran yang terjadi sepanjang satu garis lurus dengan frekuensi berbeda tetapi serupa ν 1 dan ν 2,
![]()
Persamaan lintasan suatu titik yang ikut serta dalam dua osilasi yang saling tegak lurus dengan amplitudo A 1 dan A 2 dan fase awal φ 1 dan φ 2,
Jika fase awal φ 1 dan φ 2 komponen osilasi adalah sama, maka persamaan lintasannya berbentuk
yaitu titik bergerak lurus.
Jika beda fasanya sebesar , maka persamaannya berbentuk
![]()
yaitu, titik bergerak sepanjang elips.
Persamaan diferensial osilasi harmonik suatu titik material
![]() , atau
, atau ![]() , dimana m adalah massa titik; k-
koefisien gaya kuasi-elastis ( k=Tω 2).
, dimana m adalah massa titik; k-
koefisien gaya kuasi-elastis ( k=Tω 2).
Energi total suatu titik material yang melakukan osilasi harmonik adalah
Periode osilasi suatu benda yang digantung pada pegas (pendulum pegas)
![]()
Di mana M- massa tubuh; k- kekakuan pegas. Rumus ini berlaku untuk getaran elastis dalam batas yang memenuhi hukum Hooke (dengan massa pegas yang kecil dibandingkan dengan massa benda).
Periode osilasi bandul matematika
![]()
Di mana aku- panjang pendulum; G- percepatan gravitasi. Periode osilasi bandul fisis
Di mana J- momen inersia benda yang berosilasi terhadap sumbunya
keraguan; A- jarak pusat massa bandul dari sumbu osilasi;
Mengurangi panjang pendulum fisik.
Rumus yang diberikan akurat untuk kasus amplitudo yang sangat kecil. Untuk amplitudo terbatas, rumus ini hanya memberikan hasil perkiraan. Dengan amplitudo tidak lebih besar dari, kesalahan nilai periode tidak melebihi 1%.
Periode getaran puntir suatu benda yang digantung pada benang elastis adalah
![]()
Di mana J- momen inersia benda terhadap sumbu yang bertepatan dengan benang elastis; k- kekakuan benang elastis, sama dengan rasionya momen elastis yang timbul pada saat benang dipelintir, terhadap sudut puntirnya benang.
Persamaan diferensial osilasi teredam ![]() , atau ,
, atau ,
Di mana R- koefisien resistensi; δ - koefisien redaman: ;ω 0 - frekuensi sudut alami osilasi *
![]()
Persamaan Osilasi Teredam
Di mana Pada)- amplitudo osilasi teredam saat ini T;ω adalah frekuensi sudutnya.
Frekuensi sudut osilasi teredam
![]()
О Ketergantungan amplitudo osilasi teredam terhadap waktu
![]() SAYA
SAYA
Di mana A 0 - amplitudo osilasi saat ini T=0.
Penurunan osilasi logaritmik
![]()
Di mana Pada) Dan SEBUAH(t+T)- amplitudo dua osilasi berturut-turut yang dipisahkan waktu oleh suatu periode.
Persamaan diferensial osilasi paksa
dimana adalah gaya periodik eksternal yang bekerja pada titik material yang berosilasi dan menyebabkan osilasi paksa; F 0 - nilai amplitudonya;
Amplitudo osilasi paksa
Frekuensi resonansi dan amplitudo resonansi ![]() Dan
Dan
Contoh pemecahan masalah
Contoh 1. Intinya berosilasi menurut hukum x(t)=![]() ,
Di mana SEBUAH=2 lihat Tentukan fase awal φ jika
,
Di mana SEBUAH=2 lihat Tentukan fase awal φ jika
X(0)=cm dan X , (0)<0. Построить векторную диаграмму для мо- мента T=0.
Larutan. Mari kita gunakan persamaan gerak dan nyatakan perpindahan saat ini T=0 melalui fase awal:
![]()
Dari sini kita menemukan fase awal:
![]()
* Dalam rumus getaran harmonik yang diberikan sebelumnya, besaran yang sama ditetapkan secara sederhana ω (tanpa indeks 0).
Mari kita substitusikan nilai yang diberikan ke dalam ekspresi ini X(0) dan A:φ=
= ![]() . Nilai argumen dipenuhi oleh dua nilai sudut:
. Nilai argumen dipenuhi oleh dua nilai sudut:
Untuk menentukan nilai sudut φ mana yang juga memenuhi kondisi , pertama-tama kita cari:
Mengganti nilai ke dalam ekspresi ini T=0 dan secara bergantian nilai fase awal dan, kami temukan
T  seperti biasa A>0 dan ω>0, maka hanya nilai pertama dari fase awal yang memenuhi kondisi. Jadi, fase awal yang diinginkan
seperti biasa A>0 dan ω>0, maka hanya nilai pertama dari fase awal yang memenuhi kondisi. Jadi, fase awal yang diinginkan
Dengan menggunakan nilai φ yang ditemukan, kita membuat diagram vektor (Gbr. 6.1). Contoh 2. Titik material dengan massa T=5 g melakukan osilasi harmonik dengan frekuensi ν =0,5Hz. Amplitudo osilasi A=3 cm Tentukan: 1) kecepatan υ titik pada saat terjadinya perpindahan x== 1,5cm; 2) gaya maksimum F max yang bekerja pada titik tersebut; 3) Gambar. 6.1 energi total E titik berosilasi.
dan kita memperoleh rumus kecepatan dengan mengambil turunan perpindahan pertama kali:
Untuk menyatakan kecepatan melalui perpindahan, waktu harus dikeluarkan dari rumus (1) dan (2). Caranya, kita kuadratkan kedua persamaan dan membagi persamaan pertama dengan A 2 , yang kedua di A 2 ω 2 dan tambahkan:
![]() , atau
, atau ![]()
Setelah menyelesaikan persamaan terakhir untuk υ , kita akan menemukannya
Setelah melakukan perhitungan menggunakan rumus ini, kita dapatkan
Tanda plus menunjukkan kasus ketika arah kecepatan bertepatan dengan arah positif sumbu X, tanda minus - ketika arah kecepatan bertepatan dengan arah sumbu negatif X.
Perpindahan pada osilasi harmonik, selain persamaan (1), juga dapat ditentukan dengan persamaan
Mengulangi solusi yang sama dengan persamaan ini, kita mendapatkan jawaban yang sama.
2. Kita mencari gaya yang bekerja pada suatu titik menggunakan hukum kedua Newton:
Di mana A - percepatan suatu titik, yang kita peroleh dengan mengambil turunan waktu dari kecepatan:
Mengganti ekspresi percepatan ke dalam rumus (3), kita memperoleh
Oleh karena itu nilai gaya maksimum
![]()
Substitusikan nilai π, ν ke dalam persamaan ini, T Dan A, kita akan menemukannya
![]()
3. Energi total suatu titik osilasi adalah jumlah energi kinetik dan energi potensial yang dihitung untuk setiap momen waktu.
Cara termudah untuk menghitung energi total adalah pada saat energi kinetik mencapai nilai maksimumnya. Pada saat ini energi potensialnya nol. Oleh karena itu energi totalnya E titik osilasi sama dengan energi kinetik maksimum
Kami menentukan kecepatan maksimum dari rumus (2), dengan menetapkan: ![]() . Mengganti ekspresi kecepatan ke dalam rumus (4), kita temukan
. Mengganti ekspresi kecepatan ke dalam rumus (4), kita temukan
![]()
Mengganti nilai besaran ke dalam rumus ini dan membuat perhitungan, kita mendapatkan
atau μJ.
Contoh 3. Pada ujung-ujungnya terdapat batang yang tipis dan panjang aku= 1 m dan massa M 3 =400 g bola-bola kecil yang diperkuat dengan massa M 1 =200 gram Dan M 2 =300 gram. Batang berosilasi terhadap sumbu horizontal, tegak lurus
berbentuk lingkaran pada batang dan melewati bagian tengahnya (titik O pada Gambar 6.2). Tentukan periode T osilasi yang dilakukan oleh batang.
Larutan. Periode osilasi bandul fisis, misalnya batang dengan bola, ditentukan oleh relasi
Di mana J- T - massanya; aku DENGAN - jarak dari pusat massa bandul ke sumbunya.
Momen inersia bandul ini sama dengan jumlah momen inersia bola J 1 dan J 2 dan batang J 3:
Mengambil bola untuk poin materi, mari kita nyatakan momen inersianya:
Karena sumbu melewati bagian tengah batang, momen inersianya relatif terhadap sumbu tersebut J 3 = =. Mengganti ekspresi yang dihasilkan J 1 , J 2 Dan J 3 ke dalam rumus (2), kita mencari momen inersia total bandul fisis:
Setelah melakukan perhitungan menggunakan rumus ini, kami menemukannya
Beras. 6.2 Massa bandul terdiri dari massa bola dan massa batang:
Jarak aku DENGAN Kita akan mencari pusat massa bandul dari sumbu osilasi berdasarkan pertimbangan berikut. Jika sumbu X arahkan sepanjang batang dan sejajarkan titik asal koordinat dengan titik TENTANG, maka jarak yang diperlukan aku sama dengan koordinat pusat massa pendulum, yaitu.
Mengganti nilai besaran M 1 , M 2 , M, aku dan setelah melakukan perhitungan, kami menemukannya
Setelah melakukan perhitungan menggunakan rumus (1), kita memperoleh periode osilasi bandul fisis:
Contoh 4. Pendulum fisik adalah batang yang panjangnya aku= 1 m dan massa 3 T 1 Dengan diikatkan pada salah satu ujungnya dengan lingkaran berdiameter dan massa T 1 . Sumbu horisontal Ons
pendulum melewati bagian tengah batang yang tegak lurus (Gbr. 6.3). Tentukan periode T osilasi pendulum seperti itu.
Larutan. Periode osilasi bandul fisis ditentukan oleh rumus
![]() (1)
(1)

Di mana J- momen inersia pendulum terhadap sumbu osilasi; T - massanya; aku C - jarak dari pusat massa bandul ke sumbu osilasi.
Momen inersia bandul sama dengan jumlah momen inersia batang J 1 dan lingkaran J 2:
![]() (2).
(2).
Momen inersia batang terhadap sumbu tegak lurus batang dan melewati pusat massanya ditentukan dengan rumus ![]() . Pada kasus ini t= 3T 1 dan
. Pada kasus ini t= 3T 1 dan
![]()
Kita mencari momen inersia lingkaran menggunakan teorema Steiner ![]() ,Di mana J-
momen inersia terhadap sumbu sembarang; J 0
-
momen inersia terhadap suatu sumbu yang melalui pusat massa yang sejajar dengan sumbu tertentu; A - jarak antara sumbu yang ditunjukkan. Menerapkan rumus ini ke lingkaran itu, kita dapatkan
,Di mana J-
momen inersia terhadap sumbu sembarang; J 0
-
momen inersia terhadap suatu sumbu yang melalui pusat massa yang sejajar dengan sumbu tertentu; A - jarak antara sumbu yang ditunjukkan. Menerapkan rumus ini ke lingkaran itu, kita dapatkan
Mengganti ekspresi J 1 dan J 2 ke dalam rumus (2), kita mencari momen inersia pendulum terhadap sumbu rotasi:
Jarak aku DENGAN dari sumbu pendulum ke pusat massanya adalah sama dengan
Mengganti ekspresi ke dalam rumus (1) J, aku s dan massa bandul, kita cari periode osilasinya:
Setelah menghitung menggunakan rumus ini kita dapatkan T=2,17 detik.
Contoh 5. Dua osilasi dengan arah yang sama ditambahkan, dinyatakan dengan persamaan; X 2 = =, dimana A 1 = 1 cm, A 2 =2 cm, s, s, ω = =. 1. Tentukan fase awal φ 1 dan φ 2 dari komponen osilator
Baniya. 2. Temukan amplitudonya A dan fase awal φ dari osilasi yang dihasilkan. Tuliskan persamaan getaran yang dihasilkan.
Larutan. 1. Persamaan getaran harmonik berbentuk
Mari kita ubah persamaan yang ditentukan dalam rumusan masalah ke bentuk yang sama:

Dari perbandingan ekspresi (2) dengan persamaan (1), kita menemukan fase awal osilasi pertama dan kedua:
Senang dan ![]() senang.
senang.
2. Untuk menentukan amplitudo A dari osilasi yang dihasilkan, akan lebih mudah untuk menggunakan diagram vektor yang disajikan pada beras. 6.4. Menurut teorema kosinus, kita peroleh
dimana adalah beda fasa komponen osilasi ![]() , kemudian dengan mensubstitusi nilai yang ditemukan dari φ 2 dan φ 1 kita mendapatkan rad.
, kemudian dengan mensubstitusi nilai yang ditemukan dari φ 2 dan φ 1 kita mendapatkan rad.
Mari kita gantikan nilainya A 1 , A 2 dan ke dalam rumus (3) dan lakukan perhitungan:
A= 2,65 cm.
Mari kita tentukan tangen fase awal φ dari osilasi yang dihasilkan langsung dari Gambar. 6.4: ![]() ,fase awalnya dari mana?
,fase awalnya dari mana?
![]()
Osilasi gerakan atau proses yang dicirikan oleh pengulangan tertentu dari waktu ke waktu disebut. Proses osilasi tersebar luas di alam dan teknologi, misalnya ayunan pendulum jam yang bergantian listrik dll. Ketika pendulum berosilasi, koordinat pusat massanya berubah, dalam kasus ini arus bolak-balik tegangan dan arus pada rangkaian berfluktuasi. Sifat fisik getarannya bisa berbeda-beda, oleh karena itu ada getaran mekanis, elektromagnetik, dll. Namun berbeda proses osilasi dijelaskan oleh karakteristik yang sama dan persamaan yang sama. Oleh karena itu kemanfaatannya pendekatan umum untuk mempelajari getaran dari sifat fisik yang berbeda.
Osilasi disebut bebas, jika mereka dilakukan hanya di bawah pengaruh kekuatan internal bekerja antara elemen-elemen sistem setelah sistem dipindahkan dari posisi setimbang kekuatan luar dan dibiarkan sendiri. Getaran bebas selalu osilasi teredam , karena dalam sistem nyata, kehilangan energi tidak dapat dihindari. Dalam kasus ideal suatu sistem tanpa kehilangan energi, osilasi bebas (berlanjut selama yang diinginkan) disebut memiliki.
Jenis osilasi bebas tak teredam yang paling sederhana adalah getaran harmonik - osilasi yang besaran osilasinya berubah seiring waktu menurut hukum sinus (kosinus). Getaran yang terdapat pada alam dan teknologi seringkali bersifat mendekati harmonik.
Osilasi harmonik dijelaskan dengan persamaan yang disebut persamaan osilasi harmonik:
Di mana A- amplitudo osilasi, nilai maksimum besaran osilasi X; - frekuensi osilasi alami melingkar (siklik); - fase awal osilasi pada momen waktu T= 0; - fase osilasi pada saat waktu T. Fase osilasi menentukan nilai besaran osilasi dalam saat ini waktu. Karena kosinus bervariasi dari +1 hingga -1, maka X dapat mengambil nilai dari + A sebelum - A.
Waktu T selama sistem menyelesaikan satu osilasi lengkap disebut periode osilasi. Selama T fase osilasi bertambah 2 π , yaitu
Di mana . (14.2)
Kebalikan dari periode osilasi
yaitu, jumlah osilasi lengkap yang dilakukan per satuan waktu disebut frekuensi osilasi. Membandingkan (14.2) dan (14.3) kita peroleh
Satuan frekuensi adalah hertz (Hz): 1 Hz adalah frekuensi terjadinya satu osilasi lengkap dalam 1 s.
Sistem yang dapat terjadi getaran bebas disebut osilator . Sifat-sifat apa yang harus dimiliki suatu sistem agar getaran bebas dapat terjadi di dalamnya? Sistem mekanis harus dimiliki posisi keseimbangan yang stabil, setelah keluar yang muncul gaya pemulih yang diarahkan menuju posisi setimbang. Posisi ini diketahui sesuai dengan minimum energi potensial sistem. Mari kita perhatikan beberapa sistem osilasi yang memenuhi sifat-sifat berikut.
Perubahan besaran apapun dijelaskan dengan menggunakan hukum sinus atau kosinus, maka osilasi seperti itu disebut harmonik. Mari kita perhatikan rangkaian yang terdiri dari kapasitor (yang diisi sebelum dimasukkan ke dalam rangkaian) dan induktor (Gbr. 1).
Gambar 1.
Persamaan getaran harmonik dapat dituliskan sebagai berikut:
$q=q_0cos((\omega )_0t+(\alpha )_0)$ (1)
dimana $t$ adalah waktu; $q$biaya, $q_0$-- deviasi maksimum biaya dari nilai rata-rata (nol) selama perubahan; $(\omega )_0t+(\alpha )_0$- fase osilasi; $(\alpha )_0$- fase awal; $(\omega )_0$ - frekuensi siklik. Selama periode tersebut, fase berubah sebesar $2\pi $.
Persamaan bentuk:
persamaan osilasi harmonik dalam bentuk diferensial untuk rangkaian osilasi yang tidak mengandung hambatan aktif.
Semua jenis osilasi periodik dapat secara akurat direpresentasikan sebagai jumlah osilasi harmonik, yang disebut deret harmonik.
Untuk periode osilasi suatu rangkaian yang terdiri dari kumparan dan kapasitor, kita peroleh rumus Thomson:
Jika kita membedakan ekspresi (1) terhadap waktu, kita dapat memperoleh rumus untuk fungsi $I(t)$:
Tegangan melintasi kapasitor dapat ditemukan sebagai:
Dari rumus (5) dan (6) dapat disimpulkan bahwa kuat arus mendahului tegangan pada kapasitor sebesar $\frac(\pi )(2).$
Osilasi harmonik dapat direpresentasikan baik dalam bentuk persamaan, fungsi maupun diagram vektor.
Persamaan (1) menyatakan osilasi bebas tak teredam.
Persamaan Osilasi Teredam
Perubahan muatan ($q$) pada pelat kapasitor dalam rangkaian, dengan memperhitungkan resistansi (Gbr. 2), akan dijelaskan dengan persamaan diferensial dalam bentuk:

Gambar 2.
Jika hambatan yang merupakan bagian dari rangkaian $R\
di mana $\omega =\sqrt(\frac(1)(LC)-\frac(R^2)(4L^2))$ adalah frekuensi osilasi siklik. $\beta =\frac(R)(2L)-$koefisien redaman. Amplitudo osilasi teredam dinyatakan sebagai:
Jika pada $t=0$ muatan pada kapasitor sama dengan $q=q_0$ dan tidak ada arus pada rangkaian, maka untuk $A_0$ kita dapat menulis:
Fase osilasi pada momen awal ($(\alpha )_0$) sama dengan:
Ketika $R >2\sqrt(\frac(L)(C))$ perubahan muatan bukan merupakan osilasi, pelepasan kapasitor disebut aperiodik.
Contoh 1
Latihan: Nilai tagihan maksimum adalah $q_0=10\ C$. Bervariasi secara harmonis dengan periode $T= 5 s$. Tentukan arus maksimum yang mungkin.
Larutan:
Sebagai dasar untuk memecahkan masalah kami menggunakan:
Untuk mencari kekuatan arus, ekspresi (1.1) harus dibedakan terhadap waktu:
dimana maksimum (nilai amplitudo) kekuatan arus adalah ekspresi:
Dari kondisi soal kita mengetahui nilai amplitudo muatan ($q_0=10\ C$). Anda harus mencari frekuensi alami osilasi. Mari kita nyatakan sebagai:
\[(\omega )_0=\frac(2\pi )(T)\kiri(1,4\kanan).\]
Dalam hal ini, nilai yang diinginkan akan dicari menggunakan persamaan (1.3) dan (1.2) sebagai:
Karena semua besaran dalam kondisi masalah disajikan dalam sistem SI, kami akan melakukan perhitungan:
Menjawab:$I_0=12,56\ A.$
Contoh 2
Latihan: Berapakah periode osilasi pada suatu rangkaian yang memuat induktor $L=1$H dan sebuah kapasitor, jika kuat arus dalam rangkaian tersebut berubah menurut hukum: $I\left(t\right)=-0,1sin20\ pi t\ \kiri(A \kanan)?$ Berapakah kapasitansi kapasitor tersebut?
Larutan:
Dari persamaan fluktuasi arus yang diberikan dalam kondisi masalah:
kita melihat bahwa $(\omega )_0=20\pi $, oleh karena itu, kita dapat menghitung periode Osilasi menggunakan rumus:
\ \
Menurut rumus Thomson untuk rangkaian yang berisi induktor dan kapasitor, kita mempunyai:
Mari kita hitung kapasitasnya:
Menjawab:$T=0,1$c, $C=2,5\cdot (10)^(-4)F.$
Kami melihat beberapa secara fisik secara lengkap berbagai sistem, dan memastikan bahwa persamaan gerak direduksi menjadi bentuk yang sama
Perbedaan antar sistem fisika hanya tampak pada definisi besaran yang berbeda dan dalam arti fisik yang berbeda dari variabel X: ini bisa berupa koordinat, sudut, muatan, arus, dll. Perhatikan bahwa dalam kasus ini, sebagai berikut dari struktur persamaan (1.18), besaran selalu berdimensi kebalikan waktu.
Persamaan (1.18) menjelaskan apa yang disebut getaran harmonis.
Persamaan getaran harmonik (1.18) bersifat linier persamaan diferensial orde kedua (karena mengandung turunan kedua dari variabel X). Linearitas persamaan berarti bahwa
jika beberapa fungsi x(t) adalah solusi persamaan ini, maka fungsinya Cx(t) juga akan menjadi solusinya ( C– konstanta sewenang-wenang);
jika berfungsi x 1 (t) Dan x 2(t) adalah solusi persamaan ini, lalu jumlahnya x 1 (t) + x 2 (t) juga akan menjadi solusi untuk persamaan yang sama.
Hal itu juga telah terbukti teorema matematika, yang menurutnya persamaan orde kedua memiliki dua solusi independen. Semua solusi lain, berdasarkan sifat linearitasnya, dapat diperoleh sebagai kombinasi liniernya. Mudah untuk memverifikasi dengan diferensiasi langsung bahwa fungsi independen dan memenuhi persamaan (1.18). Artinya solusi umum persamaan ini berbentuk:
Di mana C 1,dari 2- konstanta sewenang-wenang. Solusi ini dapat disajikan dalam bentuk lain. Mari masukkan nilainya
|
|
dan tentukan sudut dengan hubungan:
|
|
Maka solusi umum (1.19) ditulis sebagai
Menurut rumus trigonometri, ekspresi dalam tanda kurung adalah sama dengan
Kami akhirnya sampai pada solusi umum persamaan getaran harmonik sebagai:
Nilai non-negatif A ditelepon amplitudo getaran, - fase awal osilasi. Seluruh argumen kosinus - kombinasinya - disebut fase osilasi.
Ekspresi (1.19) dan (1.23) benar-benar ekuivalen, sehingga kita dapat menggunakan salah satunya, berdasarkan pertimbangan kesederhanaan. Kedua solusi tersebut adalah fungsi periodik waktu. Memang sinus dan kosinus bersifat periodik dengan suatu periode . Oleh karena itu, berbagai keadaan sistem yang melakukan osilasi harmonik akan berulang setelah jangka waktu tertentu T*, di mana fase osilasi menerima kenaikan yang merupakan kelipatan :
Oleh karena itu
Setidaknya saat ini
ditelepon periode osilasi (Gbr. 1.8), dan - miliknya melingkar (siklik) frekuensi.
Beras. 1.8.
Mereka juga menggunakan frekuensi fluktuasi
|
|
Dengan demikian, frekuensi melingkar sama dengan jumlah osilasi per detik
Jadi, jika sistem pada waktunya T dicirikan oleh nilai variabelnya x(t), maka variabel tersebut akan memiliki nilai yang sama setelah jangka waktu tertentu (Gbr. 1.9), yaitu
![]()
Makna yang sama secara alami akan terulang seiring berjalannya waktu 2T, ZT dll.

Beras. 1.9. Periode osilasi
Solusi umum mencakup dua konstanta sembarang ( C 1, C 2 atau A, A), yang nilainya harus ditentukan oleh dua kondisi awal. Biasanya (walaupun belum tentu) perannya dimainkan oleh nilai awal variabel x(0) dan turunannya.
Mari kita beri contoh. Biarkan penyelesaian (1.19) persamaan osilasi harmonik menggambarkan gerak bandul pegas. Nilai konstanta sembarang bergantung pada cara kita membuat pendulum keluar dari keseimbangan. Misalnya, kita menarik pegas ke kejauhan dan melepaskan bola tanpa kecepatan awal. Pada kasus ini

Mengganti t = 0 di (1.19), kita menemukan nilai konstanta dari 2
![]()
Solusinya terlihat seperti:
Kami menemukan kecepatan beban dengan diferensiasi terhadap waktu
![]()
Mengganti di sini T = 0, carilah konstanta C 1:
![]()
Akhirnya
![]()
Dibandingkan dengan (1.23), kita menemukan bahwa adalah amplitudo osilasi, dan fase awalnya adalah nol: .
Sekarang mari kita membuat pendulum tidak seimbang dengan cara lain. Mari kita pukul beban sehingga memperoleh kecepatan awal, tetapi praktis tidak bergerak saat tumbukan. Kami kemudian memiliki kondisi awal lainnya:

![]()
solusi kami sepertinya
![]()
Kecepatan beban akan berubah menurut hukum:
![]()
Mari kita gantikan di sini:
![]()