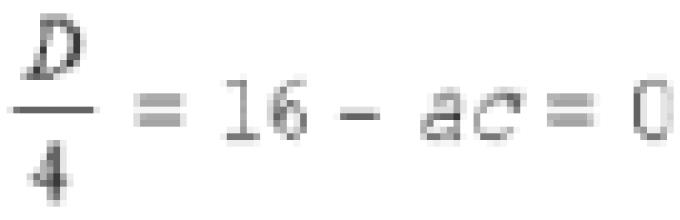Pelajaran: Bagaimana cara membuat fungsi parabola atau kuadrat?
BAGIAN TEORITIS
Parabola adalah grafik fungsi yang dijelaskan dengan rumus ax 2 +bx+c=0.
Untuk membuat parabola, Anda harus mengikuti algoritma sederhana:
1) Rumus parabola y=ax 2 +bx+c,
Jika sebuah>0 kemudian cabang-cabang parabola diarahkan ke atas,
jika tidak, cabang-cabang parabola diarahkan turun.
Anggota gratis C titik ini memotong parabola dengan sumbu OY;
2), ditemukan dengan menggunakan rumus x=(-b)/2a, kita substitusikan x yang ditemukan ke dalam persamaan parabola dan temukan kamu;
3)Fungsi nol atau dengan kata lain titik potong parabola dengan sumbu OX disebut juga akar persamaan. Untuk mencari akar-akarnya kita samakan persamaannya dengan 0 kapak 2 +bx+c=0;
Jenis persamaan:
a) Persamaan kuadrat lengkap mempunyai bentuk kapak 2 +bx+c=0 dan diselesaikan oleh pihak yang diskriminan;
b) Bentuk persamaan kuadrat tidak lengkap kapak 2 +bx=0. Untuk mengatasinya, Anda perlu mengeluarkan x dari tanda kurung, lalu menyamakan setiap faktor dengan 0:
kapak 2 +bx=0,
x(kapak+b)=0,
x=0 dan kapak+b=0;
c) Bentuk persamaan kuadrat tidak lengkap kapak 2 +c=0. Untuk mengatasinya, Anda perlu memindahkan yang tidak diketahui ke satu sisi, dan yang diketahui ke sisi lain. x =±√(c/a);
4) Temukan beberapa titik tambahan untuk membangun fungsi tersebut.
BAGIAN PRAKTIS
Jadi sekarang, dengan menggunakan sebuah contoh, kami akan menganalisis semuanya selangkah demi selangkah:
Contoh 1:
kamu=x 2 +4x+3
c=3 berarti parabola memotong OY di titik x=0 y=3. Cabang-cabang parabola menghadap ke atas karena a=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 titik sudut berada di titik (-2;-1)
Mari kita cari akar-akar persamaan x 2 +4x+3=0
Dengan menggunakan diskriminan kita menemukan akarnya
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Mari kita ambil beberapa titik sembarang yang terletak di dekat titik sudut x = -2
x -4 -3 -1 0
kamu 3 0 0 3
Substitusikan x ke dalam persamaan nilai y=x 2 +4x+3
kamu=(-4) 2 +4*(-4)+3=16-16+3=3
kamu=(-3) 2 +4*(-3)+3=9-12+3=0
kamu=(-1) 2 +4*(-1)+3=1-4+3=0
kamu=(0) 2 +4*(0)+3=0-0+3=3
Dari nilai fungsinya terlihat parabola simetris terhadap garis lurus x = -2
Contoh #2:
kamu=-x 2 +4x
c=0 artinya parabola memotong OY di titik x=0 y=0. Cabang-cabang parabola melihat ke bawah karena a=-1 -1 Cari akar persamaan -x 2 +4x=0
Persamaan kuadrat tidak lengkap berbentuk ax 2 +bx=0. Untuk mengatasinya, Anda perlu mengeluarkan x dari tanda kurung, lalu menyamakan setiap faktor dengan 0.
x(-x+4)=0, x=0 dan x=4.
Mari kita ambil beberapa titik sembarang yang terletak di dekat titik sudut x=2
x 0 1 3 4
kamu 0 3 3 0
Substitusikan x ke dalam persamaan nilai y=-x 2 +4x
kamu=0 2 +4*0=0
kamu=-(1) 2 +4*1=-1+4=3
kamu=-(3) 2 +4*3=-9+13=3
kamu=-(4) 2 +4*4=-16+16=0
Dari nilai fungsinya terlihat parabola simetris terhadap garis lurus x = 2
Contoh No.3
kamu=x 2 -4
c=4 artinya parabola memotong OY di titik x=0 y=4. Cabang-cabang parabola menghadap ke atas karena a=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 titik puncaknya berada di titik (0;- 4)
Mari kita cari akar persamaan x 2 -4=0
Persamaan kuadrat tidak lengkap berbentuk ax 2 +c=0. Untuk mengatasinya, Anda perlu memindahkan yang tidak diketahui ke satu sisi, dan yang diketahui ke sisi lain. x =±√(c/a)
x 2 =4
x 1 =2
x 2 =-2
Mari kita ambil beberapa titik sembarang yang terletak di dekat titik sudut x=0
x -2 -1 1 2
kamu 0 -3 -3 0
Substitusikan x ke dalam persamaan y= x 2 -4 nilai
kamu=(-2) 2 -4=4-4=0
kamu=(-1) 2 -4=1-4=-3
kamu=1 2 -4=1-4=-3
kamu=2 2 -4=4-4=0
Dari nilai fungsinya terlihat parabola simetris terhadap garis lurus x = 0
Langganan ke saluran di YOUTUBE untuk mengikuti semua produk baru dan bersiap bersama kami untuk ujian.
Kata pengantar dan contoh sederhana
Contoh 1. Untuk nilai a berapakah persamaan ax 2 + 2x + 1 = 0 mempunyai dua akar yang berbeda?
Larutan.
Persamaan ini kuadrat terhadap variabel x untuk a№ 0 dan mempunyai akar yang berbeda jika bersifat diskriminan
yaitu untuk a< 1.
Selain itu, jika a = 0 diperoleh persamaan 2x + 1 = 0 yang mempunyai satu akar.
Jadi, a HAI (– ɐ ; 0) DAN (0; 1).
Aturan 1. Jika koefisien x 2 dari polinomial derajat kedua mengandung suatu parameter, maka perlu dianalisis kasus ketika parameter tersebut hilang.
Contoh 2. Persamaan ax 2 + 8x + c = 0 mempunyai akar tunggal yang sama dengan 1. Berapakah a dan c?
Larutan. Mari kita mulai menyelesaikan soal dengan kasus khusus a = 0, persamaannya berbentuk 8x + c = 0. Persamaan linier ini memiliki solusi x 0 = 1 untuk c = – 8.
Ketika tidak. 0 persamaan kuadrat mempunyai akar tunggal jika ![]()
Selain itu, dengan mensubstitusikan akar x 0 = 1 ke dalam persamaan, kita memperoleh a + 8 + c = 0.
Memecahkan sistem dua persamaan linear, kita temukan a = c = – 4.
Teorema 1.
Untuk trinomial kuadrat tereduksi y = x 2 + px + q (dengan asumsi p 2і
4q)
jumlah akar-akar x 1 + x 2 = – p, hasil kali akar-akar x 1 x 2 = q, selisih akar-akarnya adalah ![]()
dan jumlah kuadrat akar-akarnya x 1 2 + x 2 2 = p 2 – 2q.
Teorema 2.
Untuk trinomial kuadrat y = ax 2 + bx + c dengan dua akar x 1 dan x 2, kita peroleh
pemuaian kapak 2 + bx + c = a(x – x 1)(x – x 2), untuk trinomial dengan satu akar x 0 – pemuaian
kapak 2 + bx + c = a(x – x 0) 2 .
Komentar. Seringkali tentang persamaan kuadrat dengan diskriminan sama dengan nol dan masing-masing memiliki satu akar, dikatakan memiliki dua akar yang berhimpitan (?). Hal ini terkait dengan faktorisasi polinomial yang diberikan pada Teorema 2.(Cara yang benar untuk mengatakan dan memahami dalam kasus ini adalah “satu akar dari kelipatan dua.” – Ed.)
Kami akan memperhatikan kehalusan ini dan menyoroti kasus akar tunggal multiplisitas 2.
Contoh 3. Pada persamaan x 2 + ax + 12 = 0, tentukan a sedemikian rupa sehingga selisih akar-akar persamaan tersebut sama dengan satu.
Larutan. Perbedaan mendasar ![]()
dari mana a = ± 7.
Contoh 4. Berapa jumlah kuadrat akar-akar persamaan 2x 2 + 4x + a = 0 sama dengan 6?
Larutan. Mari kita tulis persamaannya dalam bentuk ![]()
dari mana x 1 2 + x 2 2 = 4 – a = 6 dan a = – 2.
Contoh 5. Untuk semua a, selesaikan persamaan ax 2 – 2x + 4 = 0.
Larutan. Jika a = 0, maka x = 2. Jika a№
0, maka persamaannya menjadi kuadrat. Itu diskriminan
sama dengan D = 4 – 16a. Jika D< 0, т. е. a > ,
persamaan tersebut tidak memiliki solusi. Jika D = 0, yaitu a = ,
x = 4. Jika D > 0, yaitu a< ,
persamaan tersebut memiliki dua akar![]()
Letak akar-akar trinomial kuadrat
Grafik persamaan kuadrat adalah parabola, dan penyelesaian persamaan kuadrat adalah absis titik potong parabola tersebut dengan sumbu Ox. Dasar penyelesaian semua soal pada bagian ini adalah mempelajari ciri-ciri letak parabola dengan sifat-sifat tertentu bidang koordinat.
Contoh 6. Untuk a apakah akar-akar persamaan x 2 – 2ax + a 2 – a – 6 = 0 mempunyai tanda yang berbeda?
Solusi (Gbr. 1).

Persamaan kuadrat tidak mempunyai penyelesaian (grafiknya adalah parabola tipe D), atau mempunyai satu atau dua akar positif (parabola C), atau mempunyai satu atau dua akar negatif (parabola A), atau mempunyai akar-akar yang tandanya berbeda (parabola B).
Sangat mudah untuk memahami bahwa jenis parabola terakhir, tidak seperti parabola lainnya, dicirikan oleh fakta bahwa f(0)< 0. Таким образом, f(0) = a 2 – a – 6 < 0, откуда 0 < a < .
Solusi ini memungkinkan adanya generalisasi, yang akan kami rumuskan sebagai aturan berikut.
Aturan 2. Agar persamaan ax 2 + bx + c = 0
mempunyai dua akar yang berbeda x 1 dan x 2 sehingga x 1< M < x 2 , необходимо и достаточно, чтобы a f(M) < 0.
Contoh 7. Untuk a persamaan x 2 – 2ax + a 2 – a – 6 = 0 mempunyai dua akar berbeda yang bertanda sama?
Larutan. Kami tertarik pada parabola tipe A dan C (lihat Gambar 1). Mereka dicirikan oleh fakta bahwa
dari mana a HAI (– 6; – 2) DAN (3; + ɐ ).
Contoh 8. Untuk a apakah persamaan x 2 – 2ax + a 2 – a – 6 = 0 mempunyai dua akar positif yang berbeda?
Larutan. Kami tertarik pada parabola tipe C pada Gambar. 1.
Agar persamaan mempunyai akar, kita memerlukan![]()
Karena kedua akar persamaan harus positif dengan syarat, absis titik puncak parabola yang terletak di antara akar-akar tersebut adalah positif: x 0 = a > 0.
Ordinat puncak f(x 0)< 0 в силу того, что мы потребовали существование корней, поэтому если, кроме того, потребовать выполнение условия f(x 0) >0, maka karena kontinuitas fungsi yang diteliti, terdapat titik x 1 TENTANG (0; x 0) sehingga f(x 1) = 0. Jelas, ini adalah akar persamaan yang lebih kecil.
Jadi, f(0) = a 2 – a – 6 > 0, dan dengan menggabungkan semua kondisi, kita mendapatkan sistemnya
dengan solusi a O (3; + Ґ ).
Contoh 9. Untuk a persamaan x 2 – 2ax + a 2 – a – 6 mempunyai dua akar negatif yang berbeda?
Larutan. Setelah mempelajari parabola tipe A pada Gambar. 1, kita mendapatkan sistemnya
dari mana a O (– 6; – 2).
Mari kita menggeneralisasi solusi permasalahan sebelumnya dalam bentuk aturan berikut.
Aturan 3. Agar persamaan ax 2 + bx + c = 0 mempunyai dua akar berbeda x 1 dan x 2 yang masing-masing lebih besar (kurang dari) M, maka perlu dan cukup bahwa
Contoh 10. Fungsi f(x) diberikan oleh rumus
Temukan semua nilai parameter a yang persamaan f(x) = 0 memiliki setidaknya satu solusi.
Larutan. Semua solusi yang mungkin untuk persamaan tertentu diperoleh sebagai solusi persamaan kuadrat
x 2 – (4a + 14)x + 4a 2 + 33a + 59 = 0
dengan syarat tambahan bahwa setidaknya satu akar (yang jelas lebih besar) x 2 saya a.
Tentu saja, agar persamaan mempunyai akar-akar, persamaan tersebut harus = – 5(a + 2) і
0,
dari mana Ј – 2.
Grafik ruas kiri persamaan yang dipilih adalah parabola yang absis titik sudutnya adalah x 0 = 2a + 7. Penyelesaian masalah diberikan oleh dua jenis parabola (Gbr. 2).
A: x 0 i a, dari mana a i – 7. Dalam hal ini, akar polinomial yang lebih besar adalah x 2 saya x 0 saya a.
B: x 0< a, f(a)
Ј
0, dari mana  .
.
Dalam hal ini juga akar polinomial yang lebih besar adalah x 2 saya a.
Akhirnya  .
.
Tiga solusi untuk satu ketidaksetaraan
Contoh 11. Tentukan semua nilai parameter a yang pertidaksamaannya x 2 – 2ax + a 2 + 2a – 3 > 0
dilakukan:
1) untuk semua nilai x;
2) di depan semua orang nilai-nilai positif X;
3) untuk semua nilai x HAI [– 1; 1].
Larutan.
Cara pertama.
1) Jelasnya, pertidaksamaan ini berlaku untuk semua x jika diskriminannya negatif, yaitu.
= sebuah 2 – (sebuah 2 + 2a – 3) = – 2a + 3< 0,
dari mana >.
2) Untuk lebih memahami apa yang diperlukan dalam rumusan masalah, mari kita gunakan teknik sederhana: gambar beberapa parabola pada bidang koordinat, lalu ambil dan tutup setengah bidang kiri relatif terhadap sumbu Oy. Bagian parabola yang tetap terlihat harus berada di atas sumbu Sapi.
Kondisi masalah dipenuhi dalam dua kasus (lihat Gambar 3):
< 0, откуда a > ;
B: kedua akar (mungkin satu, tapi ganda) persamaan x 2 – 2ax + a 2 + 2a – 3 = 0 berada di sebelah kiri titik asal. Menurut aturan 3, kondisi ini setara dengan sistem pertidaksamaan D dan 0, x 0 dan 0 dan f(0) dan 0.
Namun, ketika menyelesaikan sistem ini, pertidaksamaan pertama dapat dihilangkan, karena meskipun beberapa nilai a tidak memenuhi kondisi Dі 0, maka otomatis jatuh ke dalam solusi titik A. Jadi, kita menyelesaikan sistemnya
dari mana Ј – 3.
Menggabungkan solusi titik A dan B, kita peroleh
menjawab: ![]()
3) Kondisi masalah dipenuhi dalam tiga kasus (lihat Gambar 4):
A: grafik fungsi y = x 2 – 2ax + a 2 + 2a – 3 terletak di atas sumbu Ox yaitu D< 0, откуда a > ;
B: kedua akar (mungkin salah satu dari kelipatan 2) persamaan x 2 – 2ax + a 2 + 2a – 3 = 0 berada di sebelah kiri – 1. Kondisi ini setara, seperti yang kita ketahui dari aturan 3, dengan sistem kesenjangan Dі 0, x 0< – 1, f(– 1) > 0;
C: kedua akar persamaan x 2 – 2ax + a 2 + 2a – 3 = 0 berada di sebelah kanan 1.
Kondisi ini setara dengan D saya 0, x 0 > 1, f(1) > 0.
Namun pada poin B dan C, serta pada penyelesaian soal sebelumnya, pertidaksamaan yang terkait dengan diskriminan dapat dihilangkan.
Dengan demikian, kita memperoleh dua sistem ketidaksetaraan
Setelah mempertimbangkan semua kasus, kita mendapatkan hasil: a >
pada intinya
di C.
Jawaban dari permasalahan tersebut adalah dengan menggabungkan ketiga himpunan tersebut.
Cara kedua. Agar kondisi masing-masing dari tiga poin masalah terpenuhi, nilai terkecil dari fungsi tersebut
y = x 2 – 2ax + a 2 + 2a – 3 pada setiap interval yang bersesuaian harus positif.
1) Titik puncak parabola y = x 2 – 2ax + a 2 + 2a – 3 berada di titik (a; 2a – 3), maka nilai fungsi terkecil pada seluruh garis bilangan adalah 2a – 3, dan sebuah > .
2) pada setengah sumbu x i 0 nilai terkecil dari fungsi tersebut adalah f(0) = a 2 + 2a – 3, jika a< 0, и f(a) = 2a – 3, если a
і
0. Menganalisis kedua kasus tersebut, kita peroleh ![]()
3) Yang terkecil pada ruas [– 1; 1] nilai fungsi adalah
Karena nilai terkecil harus positif, kita memperoleh sistem pertidaksamaan
Solusi dari ketiga sistem ini adalah himpunan
Cara ketiga. 1) Titik puncak parabola y = x 2 – 2ax + a 2 + 2a – 3
terletak di titik (a; 2a – 3). Mari kita menggambar himpunan pada bidang koordinat yang dibentuk oleh simpul-simpul semua parabola untuk a yang berbeda (Gbr. 5).
Ini adalah garis y = 2x – 3. Ingatlah bahwa setiap titik pada garis ini memiliki nilai parameternya sendiri, dan dari setiap titik pada garis ini sebuah parabola yang sesuai dengan nilai parameter tertentu “keluar”. Parabola yang seluruhnya berada di atas sumbu Ox dicirikan oleh kondisi 2a – 3 > 0.
2) Penyelesaian titik ini adalah semua penyelesaian titik pertama, dan sebagai tambahan, parabola yang a negatif, dan f(0) = a 2 + 2a – 3і 0.
3) Dari Gambar. 5 jelas bahwa kita tertarik pada parabola yang a negatif dan f(– 1) = a 2 + 4a – 2 > 0,
atau a positif dan f(1) = a 2 – 2 > 0.
Persamaan dan pertidaksamaan yang direduksi menjadi persamaan kuadrat
Contoh 12. Berapa nilai a yang persamaan 2x 4 – 2ax 2 + a 2 – 2 = 0 tidak mempunyai penyelesaian?
Larutan. Dengan melakukan substitusi y = x 2, diperoleh persamaan kuadrat f(y) = 2y 2 – 2ay + a 2 – 2 = 0.
Persamaan yang dihasilkan tidak memiliki solusi ketika D< 0. Кроме того, первоначальное уравнение не имеет решений, когда корни уравнения f(y) = 0 отрицательны.
Kondisi tersebut dapat dituliskan sebagai suatu himpunan
Di mana ![]()
Contoh 13. Untuk setiap nilai parameter a, selesaikan persamaan cos x sin 2x = asin 3x.
Larutan. Karena 2cos x sin 2x = sin x + sin 3x dan sin 3x = 3sin x – 4sin 3 x,
maka persamaannya akan ditulis sebagai sin x (sin 2 x (4a – 2) – (3a – 2)) = 0.
Dari sini kita memperoleh solusi x = p n, n HAI Z untuk setiap a. Persamaannya ![]()
memiliki solusi 
tidak bertepatan dengan solusi persamaan pertama, hanya dengan syarat ![]()
Pembatasan yang terakhir ini setara
Jawaban: x = p n, n O Z untuk setiap a; Di samping itu,
Contoh 14. Temukan semua nilai parameter a, yang masing-masing memiliki pertidaksamaan
a 2 + 2a – sin 2 x – 2acos x > 2 berlaku untuk bilangan apa pun x.
Larutan. Mari kita ubah pertidaksamaan tersebut menjadi bentuk cos 2 x – 2acos x + a 2 + 2a – 3 > 0
dan lakukan penggantian t = cos x. Penting untuk dicatat bahwa parameter t berkisar antara – 1 hingga 1, sehingga masalahnya dapat dirumuskan ulang sebagai berikut: temukan semua a sedemikian sehingga
t 2 – 2pada + a 2 + 2a – 3 > 0
berlaku untuk semua t TENTANG [- 1; 1]. Kami telah memecahkan masalah ini sebelumnya.
Contoh 15. Tentukan berapa nilai a persamaan log 3 (9 x + 9a 3) = x yang mempunyai solusi dan temukan solusinya.
Larutan. Mari kita ubah persamaan tersebut menjadi bentuk 9 x – 3 x + 9a 3 = 0
dan dengan melakukan penggantian y = 3 x, kita mendapatkan y 2 – y + 9a 3 = 0.
Jika diskriminannya negatif, persamaan tersebut tidak memiliki solusi. Ketika diskriminan
D = 1 – 36a 3 = 0, persamaan mempunyai akar tunggal,
dan x = – log 3 2. Terakhir, jika diskriminannya positif, yaitu,
persamaan aslinya mempunyai satu akar  ,
,
dan jika, sebagai tambahan, ekspresi 1 positif,
maka persamaan tersebut juga memiliki akar kedua ![]() .
.
Jadi, kami akhirnya mendapatkannya 
![]() ,
,
tidak ada solusi untuk sisa a.
Contoh 16. Untuk setiap nilai parameter a, selesaikan persamaan dosa 4 x + cos 4 x + sin 2 x + a = 0.
Larutan. Karena
Mari kita tulis ulang persamaan tersebut dalam bentuk sin 2 x – 2sin x – 2a – 2 = 0.
Misal y = sin 2x, maka y 2 – 2y – 2a – 2 = 0 (| y | J 1).
Grafik fungsi di ruas kiri persamaan adalah parabola dengan titik sudut yang absisnya y 0 = 1; nilai fungsi di titik y = – 1 adalah 1 – 2a; diskriminan persamaan tersebut adalah 8a + 12. Artinya akar yang lebih besar y 2 dari persamaan y 2 – 2y – 2a – 2 = 0, meskipun ada, lebih besar dari 1, dan persamaan yang bersangkutan sin 2x = y 2 tidak mempunyai solusi. 3. Untuk nilai a berapakah persamaan 2x 2 + (3a + 1)x + a 2 + a + 2 = 0 mempunyai paling sedikit satu akar?
4. Persamaan ax 2 + bx + 5 = 0 mempunyai akar tunggal yang sama dengan 1. Berapakah a dan b?
5. Untuk nilai parameter a berapakah akar-akar persamaan kuadrat 5x 2 – 7x + a = 0 mempunyai hubungan 2 sampai 5?
6. Pada persamaan ax 2 + 8x + 3 = 0, tentukan a sehingga selisih akar-akar persamaan tersebut sama dengan satu.
7. Untuk a berapakah jumlah kuadrat akar-akar persamaan x 2 – 2ax + 2(a + 1) = 0 sama dengan 20?
8. Untuk b dan c apakah persamaan c + bx – 2x 2 = 0 mempunyai satu akar positif dan satu akar negatif?
9. Tentukan semua nilai parameter a yang salah satu akar persamaannya x 2 – (a + 1)x + 2 = 0 lebih besar dari a, dan akar lainnya lebih kecil dari a.
10. Tentukan semua nilai parameter a yang persamaan x 2 + (a + 1)x + 2 = 0 mempunyai dua akar berbeda yang bertanda sama.
11. Berapa nilai a yang seluruh hasil akar persamaan (a – 3)x 2 – 2ax + 6a = 0 positif?
12. Untuk a apakah semua akar persamaan (1 + a)x 2 – 3ax + 4a = 0 lebih besar dari 1?
13. Tentukan semua nilai parameter a yang kedua akar persamaan x 2 + x + a = 0 yang berbeda lebih besar dari a.
14. Berapa nilai a yang kedua akar persamaan 4x 2 – 2x + a = 0 terletak di antara – 1 dan 1?
15. Untuk nilai a berapakah persamaan x 2 + 2(a – 1)x + a + 5 = 0 mempunyai paling sedikit satu akar positif?
16. Fungsi f(x) diberikan oleh rumus
Temukan semua nilai parameter a yang persamaan f(x) = 0 memiliki setidaknya satu solusi.
17. Untuk a apakah pertidaksamaan (a 2 – 1)x 2 + 2(a – 1)x + 2 > 0 benar untuk semua x?
18. Untuk nilai parameter a berapakah pertidaksamaan ax 2 + 2x > 1 – 3a berlaku untuk semua x positif?
19. Untuk nilai a berapakah persamaan x 4 + (1 – 2a)x 2 + a 2 – 1 = 0 tidak mempunyai penyelesaian?
20. Berapa nilai parameter a persamaan 2x 4 – 2ax 2 + a2 – 2 = 0 mempunyai satu atau dua solusi?
21. Untuk setiap nilai a, selesaikan persamaan acos x cos 2x = cos 3x.
22. Temukan semua nilai parameter a, yang masing-masing memiliki pertidaksamaan cos 2 x + 2asin x – 2a< a 2
– 4 выполняется для любого числа x.
23. Untuk semua a, selesaikan persamaan log 2 (4 x + a) = x.
24. Untuk setiap nilai parameter a, selesaikan persamaan sin 2 x + asin 2 2x = sin.
Grafik trinomial kuadrat
2019-04-19
Trinomial persegi
Kami menyebut trinomial persegi sebagai fungsi rasional derajat kedua:
$y = kapak^2 + bx + c$, (1)
di mana $a \neq 0$. Mari kita buktikan bahwa grafik trinomial kuadrat adalah parabola yang diperoleh dengan pergeseran sejajar (searah sumbu koordinat) dari parabola $y = ax^2$. Untuk melakukan ini, kami menyajikan ekspresi (1) menggunakan sederhana transformasi identitas dalam pikiran
$y = a(x + \alfa)^2 + \beta$. (2)
Transformasi terkait, yang ditulis di bawah, dikenal sebagai "ekstraksi kuadrat tepat":
$y = x^2 + bx + c = a \kiri (x^2 + \frac(b)(a) x \kanan) + c = a \kiri (x^2 + \frac(b)(a) x + \frac (b^2)(4a^2) \kanan) - \frac (b^2)(4a) + c = a \kiri (x + \frac(b)(2a) \kanan)^2 - \frac (b^2 - 4ac)(4a)$. (2")
Kami telah mengurangi trinomial kuadrat menjadi bentuk (2); di mana
$\alpha = \frac(b)(2a), \beta = - \frac (b^2 - 4ac)(4a)$
(ekspresi ini tidak boleh dihafal; akan lebih mudah untuk mengubah trinomial (1) ke bentuk (2) secara langsung setiap kali).
Sekarang jelas bahwa grafik trinomial (1) adalah parabola yang sama dengan parabola $y = ax^2$ dan diperoleh dengan menggeser parabola $y = ax^2$ searah sumbu koordinat sebesar $\ alpha$ dan $\beta$ (dengan memperhitungkan tanda $\alpha$ dan $\beta$) masing-masing. Titik puncak parabola ini terletak di titik $(- \alpha, \beta)$, sumbunya adalah garis lurus $x = - \alpha$. Untuk $a > 0$ titik puncaknya adalah titik terendah parabola, seharga $a
Sekarang mari kita mempelajari trinomial kuadrat, yaitu kita akan mengetahui sifat-sifatnya bergantung pada nilai numerik koefisien $a, b, c$ dalam ekspresinya (1).
Dalam persamaan (2") kami menyatakan nilai $b^2- 4ac$ dengan $d$:
$y = a \kiri (x + \frac(b)(2a) \kanan)^2 - \frac(d)(4a)$; (4)
$d = b^2 - 4ac$ disebut diskriminan trinomial kuadrat. Sifat-sifat trinomial (1) (dan letak grafiknya) ditentukan oleh tanda diskriminan $d$ dan koefisien utama $a$.

1) $a > 0, hari 0$; karena $a > 0$, maka graf tersebut terletak di atas titik sudut $O^( \prime)$; itu terletak di setengah bidang atas ($y > 0$ - Gambar. a.).
2) $a
3) $a > 0, d > 0$. Titik sudut $O^( \prime)$ terletak di bawah sumbu $Ox$, parabola memotong sumbu $Ox$ di dua titik $x_1, x_2$ (Gbr. c.).
4) $a 0$. Titik sudut $O^( \prime)$ terletak di atas sumbu $Ox$, parabola kembali memotong sumbu $Ox$ di dua titik $x_1, x_2$ (Gbr. d).
5) $a > 0, d = 0$. Titik sudutnya terletak pada sumbu $Ox$ itu sendiri, parabola terletak di setengah bidang atas (Gbr. e).
6) $a
Kesimpulan. Jika $d 0$), atau lebih rendah (jika $a
Jika $d > 0$, maka fungsinya bergantian (grafik sebagian terletak di bawah dan sebagian lagi di atas sumbu $Ox$). Trinomial persegi dengan $d > 0$ mempunyai dua akar (nol) $x_1, x_2$. Untuk $a > 0$ bernilai negatif pada interval antara akar-akar (Gbr. c) dan positif di luar interval ini. Pada $a
Definisi
Parabola disebut grafik fungsi kuadrat $y = ax^(2) + bx + c$, dimana $a \neq 0$.
Grafik fungsi $y = x^2$.
Untuk memplot secara skematis grafik fungsi $y = x^2$, kita akan menemukan beberapa titik yang memenuhi persamaan ini. Untuk memudahkan, kami menuliskan koordinat titik-titik tersebut dalam bentuk tabel:
Grafik fungsi $y = ax^2$.
Jika koefisien $a > 0$, maka graf $y = ax^2$ diperoleh dari graf $y = x^2$ baik dengan cara regangan vertikal (untuk $a > 1$) maupun kompresi ke $x$ sumbu (untuk $0< a < 1$). Изобразим для примера графики $y = 2x^2$ и $y = \dfrac{x^2}{2}$:
| $y = 2x^2$ | $y = \dfrac(x^2)(2)$ |
|
|
Jika $a< 0$, то график функции $y = ax^2$ можно получить из графика $y = |a|x^2$, отразив его симметрично относительно оси $x$. Построим графики функций $y = - x^2$, $y = -2x^2$ и $y = - \dfrac{x^2}{2}$:
| $y = -x^2$ | $y = -2x^2$ | $y = - \dfrac(x^2)(2)$ |
|
|
|
Grafik fungsi kuadrat.
Untuk membuat grafik fungsi $y = ax^2 + bx + c$, Anda perlu mengisolasi $ax^2 + bx + c$ dari trinomial persegi persegi sempurna, yaitu merepresentasikannya dalam bentuk $a(x - x_0)^2 + y_0$. Grafik fungsi $y = a(x - x_0)^2 + y_0$ diperoleh dari grafik $y = ax^2$ yang bersesuaian dengan menggeser sebesar $x_0$ sepanjang sumbu $x$, dan sebesar $y_0$ sepanjang sumbu $y$. Akibatnya, titik $(0;0)$ akan berpindah ke titik $(x_0;y_0)$.
Definisi
Atas parabola $y = a(x - x_0)^2 + y_0$ adalah titik dengan koordinat $(x_0;y_0)$.
Mari kita buat parabola $y = 2x^2 - 4x - 6$. Memilih persegi lengkap, kita mendapatkan $y = 2(x - 1)^2 - 8$.
| Mari kita plot $y = 2x^2$ | Mari kita pindahkan ke kanan sebanyak 1 | Dan turun jam 8 |
|
|
|
Hasilnya adalah parabola dengan titik puncaknya di titik $(1;-8)$.
Grafik fungsi kuadrat $y = ax^2 + bx + c$ memotong sumbu $y$ di titik $(0; c)$ dan sumbu $x$ di titik $(x_(1,2) ;0)$, dengan $x_(1,2)$ adalah akar-akar persamaan kuadrat $ax^2 + bx + c = 0$ (dan jika persamaan tersebut tidak mempunyai akar, maka parabola yang bersesuaian tidak memotong $ x$ sumbu).
Misalnya, parabola $y = 2x^2 - 4x - 6$ memotong sumbu di titik $(0; -6)$, $(-1; 0)$ dan $(3; 0)$.