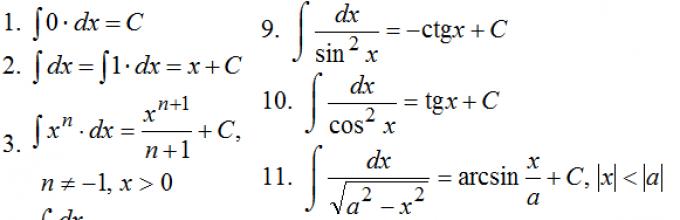Empat metode utama integrasi tercantum di bawah ini.
1)
Aturan untuk mengintegrasikan jumlah atau selisih.
.
Di sini dan di bawah u, v, w adalah fungsi dari variabel integrasi x.
2)
Memindahkan konstanta ke luar tanda integral.
Misalkan c adalah konstanta yang tidak bergantung pada x. Kemudian dapat dikeluarkan dari tanda integralnya.
3)
Metode penggantian variabel.
Mari kita pertimbangkan integral tak tentu.
Jika kita dapat menemukan fungsi seperti itu φ (X) dari x, jadi
,
kemudian, dengan mengganti variabel t = φ(x) , kita mendapatkan
.
4)
Rumus integrasi per bagian.
,
dimana u dan v adalah fungsi dari variabel integrasi.
Tujuan akhir dari perhitungan integral tak tentu- ini adalah, melalui transformasi, untuk mereduksi suatu integral tertentu menjadi integral paling sederhana, yang disebut integral tabel. Integral tabel dinyatakan dalam fungsi dasar menggunakan rumus yang diketahui.
Lihat Tabel Integral >>>
Contoh
Hitung integral tak tentu
Larutan
Kita perhatikan bahwa integral adalah jumlah dan selisih tiga suku:
, Dan .
Menerapkan metode 1
.
Selanjutnya, kita perhatikan bahwa integral dari integral baru dikalikan dengan konstanta 5, 4,
Dan 2
, masing-masing. Menerapkan metode 2
.
Dalam tabel integral kita menemukan rumusnya
.
Dengan asumsi n = 2
, kita cari integral pertama.
Mari kita tulis ulang integral kedua dalam bentuk
.
Kami memperhatikan hal itu. Kemudian
Mari kita gunakan cara ketiga. Kita ubah variabel t = φ (x) = catatan x.
.
Dalam tabel integral kita menemukan rumusnya
Karena variabel integrasi dapat dilambangkan dengan huruf apa saja, maka
Mari kita tulis ulang integral ketiga dalam bentuk
.
Kami menerapkan rumus integrasi per bagian.
Mari kita jelaskan.
Kemudian
;
;
;
;
.
Akhirnya kita punya
.
Mari kita kumpulkan suku-sukunya dengan x 3
.
.
Menjawab
Referensi:
N.M. Gunther, RO. Kuzmin, Kumpulan Masalah Matematika Tinggi, “Lan”, 2003.
Integrasi adalah salah satu operasi utama dalam analisis matematika. Tabel antiturunan yang diketahui mungkin berguna, tetapi sekarang, setelah munculnya sistem aljabar komputer, tabel tersebut kehilangan arti pentingnya. Di bawah ini adalah daftar primitif yang paling umum.
Tabel integral dasar
Pilihan ringkas lainnya

Tabel integral fungsi trigonometri
Dari fungsi rasional
Dari fungsi yang tidak rasional
Integral fungsi transendental

"C" adalah konstanta integrasi sembarang, yang ditentukan jika nilai integral pada suatu titik diketahui. Setiap fungsi mempunyai jumlah antiturunan yang tak terhingga.
Sebagian besar anak sekolah dan siswa mengalami masalah dalam menghitung integral. Halaman ini berisi tabel integral dari fungsi trigonometri, rasional, irasional dan transendental yang akan membantu dalam penyelesaiannya. Tabel turunan juga akan membantu Anda.
Video - cara mencari integral
Jika Anda belum begitu paham topik ini, tonton videonya, yang menjelaskan semuanya secara detail.Tabel antiturunan
Dengan menggunakan sifat-sifat integral tak tentu dan tabel integral fundamental,
Anda dapat mengintegrasikan beberapa fungsi.
TEKNIK INTEGRASI
Metode substitusi
Metode yang paling umum dalam mengintegrasikan fungsi adalah metode
substitusi, yang diterapkan ketika integral yang dicari
bersifat tabel, tetapi melalui serangkaian transformasi dasar hal itu dapat terjadi
direduksi menjadi sebuah tabel.
variabel t diganti dengan variabel / menggunakan rumus x=φ(t) dan,
oleh karena itu, dx adalah produk dari φ"(t)dt.
Integrasi berdasarkan bagian
Contoh: Anda perlu mencari integralnya
Di sini, garis vertikal ganda mengapit semua perhitungan itu
adalah persiapan untuk menerapkan rumus integrasi
bagian. Entri persiapan dapat diambil di luar persamaan.
INTEGRAL PASTI
Tugas. Tentukan pertambahan fungsi yang merupakan antiturunan dari fungsi f(x), kapan
transisi argumen x dari nilai a ke nilai b.
Larutan. Mari kita asumsikan bahwa melalui integrasi kita telah menemukan
Seperti yang bisa kita lihat, dalam ekspresi kenaikan fungsi antiturunan F(x) + C 1
tidak ada nilai konstanta C1. Dan karena C 1 berarti apa saja
nomor yang diberikan, maka hasil yang diperoleh menghasilkan kesimpulan sebagai berikut: kapan
transisi argumen x dari nilai x=a ke nilai x=b, semua fungsi F(x) + C,
antiturunan untuk fungsi tertentu f(x) memiliki kenaikan yang sama dengan
F(b)-F(a).
Kenaikan ini biasanya disebut integral tertentu dan dilambangkan
simbol
Jadi, integral yang diperlukan sama dengan 6.
Arti geometris integral tertentu
1. Temukan luas salah satu busur sinusoidal.
Tubuh revolusi ditunjukkan pada gambar.
Untuk pesawat saya akan memilih pesawat xy.
Contoh No.2. Mencari integral tertentu dengan metode perubahan variabel
integrasi
Contoh No.3. Menemukan integral tertentu dengan mengintegrasikannya
bagian.
Hubungan antara massa m dan kepadatan p:
Hubungan antara muatan listrik q dan kekuatan saat ini I:
Hubungan antara kapasitas kalor c dan banyaknya kalor Q:
Deskripsi pergerakan cairan kental, darah melalui pembuluh, distribusi
tekanan darah dalam sistem kardiovaskular, termal, listrik,
proses magnetik dan optik yang berhubungan dengan kehidupan
organisme, membutuhkan penggunaan integrasi.
PELATIHAN: CONTOH PEMECAHAN
titik berubah menurut hukum v = (6t +7) m/s
Tentukan bagaimana jarak yang ditempuh bergantung pada waktu jika kecepatan benda
titik berubah menurut hukum v = (6t +7) m/s, jika diketahui pada momen awal
waktu (t=0), poin materi berada pada jarak s 0 = 4 m dari titik awal
Hitunglah usaha yang dilakukan pegas ketika pegas diperpanjang dari x 1 ke x 2.
Larutan.
Untuk mengintegrasikan fungsi ini, Anda perlu melakukan penggantian
variabel
Karena terdapat 4 2 ≤2 pada ruas [-1;2], maka luas S dari gambar tersebut dihitung
dengan cara berikut:
Larutan.
kamu=sinx
du = cosxdx
batas integrasi baru: u 1 = 0 (karena x 1 = 0, mari kita substitusikan nilai ini ke nilai baru
fungsi - u = sinx, u 1 = sinx 1 = 0)
munculnya arus induksi di dalamnya,
| |
| menjawab: |
PERSAMAAN DIFERENSIAL
Persamaan diferensial adalah persamaan yang mengandung syarat-syarat
fungsi, turunannya dari berbagai ordo dan variabel bebas.
Teori persamaan diferensial muncul pada akhir abad ke-17 di bawah
pengaruh kebutuhan mekanika dan disiplin ilmu alam lainnya,
pada dasarnya bersamaan dengan kalkulus integral dan
kalkulus diferensial.
Persamaan diferensial paling sederhana telah ditemukan dalam karya I.
Newton dan G. Leibniz; istilah "persamaan diferensial"
milik Leibniz. Soal mencari integral tak tentu F(x)
fungsi f(x) Newton dianggap sederhana sebagai kasus spesial yang kedua
tugas. Inilah pendekatan yang dilakukan Newton, sebagai pencipta fondasi
ilmu alam matematika sepenuhnya dibenarkan: dalam skala yang sangat besar
Dalam banyak kasus, hukum alam yang mengatur proses tertentu,
dinyatakan dalam bentuk persamaan diferensial, dan perhitungan alirannya
proses direduksi menjadi penyelesaian persamaan diferensial.
Dua berikutnya contoh sederhana dapat dijadikan sebagai ilustrasi
apa yang dikatakan.
1) Jika suatu benda dipanaskan sampai suhu T ditempatkan dalam suatu medium yang suhunya
yang sama dengan nol, maka dalam kondisi tertentu kita dapat berasumsi bahwa
kenaikan ΔT (negatif dalam kasus T> 0) suhunya lebih kecil
interval waktu Δt dinyatakan dengan rumus yang cukup akurat
di mana k adalah koefisien konstan. Saat memproses ini secara matematis
masalah fisik percaya bahwa persis sesuai
rasio pembatas antar perbedaan
yaitu hal itu terjadi persamaan diferensial
dimana T menunjukkan turunan no t.
meregangkan pegas, membawa beban ke dalam
pergerakan. Jika x(t) menunjukkan
besarnya penyimpangan tubuh dari
posisi keseimbangan saat ini
waktu t, maka percepatan benda
dinyatakan dengan turunan ke-2 x" (t).
Gaya tx" (t) yang bekerja pada benda tersebut adalah
dengan bentangan kecil mata air
menurut hukum teori elastisitas sebanding dengan simpangan x (t). Itu.,
kita mendapatkan persamaan diferensial
 |
| Solusinya terlihat seperti: |