• Berikan gambaran tentang kelas masalah baru - konstruksi bentuk geometris menggunakan kompas dan penggaris tanpa pembagian skala.
  • Perkenalkan konsep GMT.
  • Definisikan garis-garis tegak lurus, ajarkan cara membangunnya, dan buktikan teorema tentang garis-garis tegak lurus serta inversnya.
  • Dengan menggunakan sistem gambar komputer “Compass-3D”, lakukan konstruksi geometris, yang direkomendasikan untuk dilakukan dalam kursus geometri menggunakan kompas dan penggaris.

    • Handout (Lampiran No. 1)

    Masalah yang melibatkan konstruksi dengan kompas dan penggaris tanpa pembagian paling sering diselesaikan menurut skema tertentu:

    SAYA. Analisis: Gambarkan gambar yang diinginkan secara skematis dan buat hubungan antara data tugas dan elemen yang diperlukan.

    II. Konstruksi: Sesuai rencana, pembangunan dilakukan dengan menggunakan kompas dan penggaris.

    AKU AKU AKU. Bukti: Buktikan bahwa gambar yang dibangun memenuhi kondisi masalah.

    IV. Belajar: Melakukan studi untuk melihat apakah suatu permasalahan mempunyai solusi untuk setiap data tertentu dan, jika ya, berapa banyak solusi yang ada (tidak dilakukan pada semua permasalahan).

    Berikut beberapa contoh tugas konstruksi dasar yang akan kami pertimbangkan:

    1. Sisihkan satu ruas yang sama dengan ruas tertentu (dipelajari sebelumnya).

    2. Konstruksi garis bagi yang tegak lurus suatu ruas:

    • membangun bagian tengah segmen tertentu;
    • buatlah sebuah garis yang melalui suatu titik tertentu dan tegak lurus terhadap suatu garis tertentu (titik tersebut mungkin terletak atau tidak terletak pada suatu garis tertentu).

    3. Konstruksi garis bagi sudut.

    4. Membangun sudut yang sama dengan sudut tertentu.

    Garis bagi tegak lurus ke segmen tersebut.

    Definisi: Garis bagi yang tegak lurus suatu ruas adalah garis yang melalui titik tengah ruas tersebut dan tegak lurus terhadap ruas tersebut.

    Tugas: “Buatlah garis bagi yang tegak lurus terhadap ruas tersebut.” Presentasi

    O - AB tengah

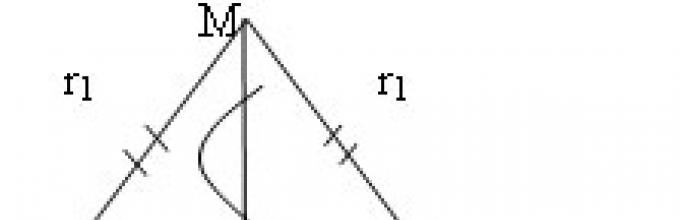
    Deskripsi konstruksi ( geser nomor 4):

    Balok a; A – awal balok

    Keliling (A; r =m)

    Lingkaran a = B; AB = m

    Lingkaran 1 (A; r 1 > m/2)

    Lingkaran 2 (B; r 1)

    Lingkaran 1 Lingkaran 2 =

    M N; MN AB =0, (MN = L)

    dimana MN AB, O – bagian tengah AB

    AKU AKU AKU. Bukti(slide nomor 5, 6)

    1. Pertimbangkan AMN dan BNM:

    AM = MB=BN=AN=r 2, maka AM = BN, AN = BM MN – sisi persekutuan

    (Gambar 3)

    Jadi AMN = BNM (di 3 sisi),

    Karena itu

    1= 2 (menurut definisi sama)

    3= 4 (menurut definisi sama)

    2. MAN dan NBM sama kaki (menurut definisi) ->

    1 = 4 dan 3 = 2 (menurut sifat sama kaki)

    3. Dari titik 1 dan 2 -> 1 = 3 maka MO adalah garis bagi AMB sama kaki

    4. Dengan demikian kita telah membuktikan bahwa MN adalah garis bagi yang tegak lurus ruas AB

    IV. Belajar

    Tugas ini punya satu-satunya keputusan, Karena setiap segmen hanya memiliki satu titik tengah, dan melalui suatu titik tertentu seseorang dapat menggambar satu garis lurus yang tegak lurus terhadap titik tersebut.

    Definisi: Kumpulan geometris poin (GMT) adalah himpunan titik yang mempunyai sifat tertentu. (Lampiran No.2)

    GMT yang Anda tahu:

    1. Garis bagi yang tegak lurus suatu ruas adalah himpunan titik-titik yang berjarak sama dari ujung-ujung ruas tersebut.
    2. Garis bagi suatu sudut - sekumpulan titik yang berjarak sama dari sisi-sisi sudut

    Jadi, mari kita buktikan teoremanya:

    Teorema: “Setiap titik pada garis-bagi yang tegak lurus terhadap suatu ruas mempunyai jarak yang sama dari ujung-ujung ruas tersebut.”

    (Gambar 4)

    Diberikan: AB; MO – garis bagi tegak lurus

    Buktikan: AM = VM

    Bukti:

    1. MO – garis bagi tegak lurus (sesuai syarat) -> O – titik tengah ruas AB, MOAB

    2. Pertimbangkan AMO dan VMO - persegi panjang

    MO – kaki umum

    		 AO = VO (O – tengah AB) -> AMO = VMO (dengan 2 kaki) -> AM = VM (menurut definisi segitiga sama kaki, sebagai sisi-sisi yang bersesuaian)

    Q.E.D

    Pekerjaan Rumah: “Buktikan teorema kebalikan dari teorema ini”

    Dalil: “Setiap titik yang berjarak sama dari ujung suatu ruas terletak pada garis bagi yang tegak lurus ruas tersebut.”

    (Gambar 5)

    Diberikan: AB; MA=MV

    Membuktikan: Titik M terletak pada garis bagi yang tegak lurus

    Bukti:

    Itu. MO adalah garis bagi tegak lurus yang memuat semua titik yang berjarak sama dari ujung-ujung ruas tersebut.

    Sifat-sifat garis bagi yang tegak lurus terhadap sisi-sisi suatu segitiga

    Mereka berpotongan di satu titik dan titik ini adalah pusat lingkaran yang dibatasi di sekitar segitiga, yang akan kita pelajari di kelas delapan.

    Bengkel

    Bahan dan peralatan teknis:

    Distribusi: 29.574 KB

    OS: Windows 9x/2000/XP

    Situs web: http://www.ascon.ru

    Sekarang mari kita transfer konstruksinya ke lingkungan grafis komputer (slide nomor 7)

    Pengetahuan dan keterampilan yang diperoleh sebelumnya harus diterapkan pada tugas tertentu. Anda akan melihat bahwa konstruksi tidak akan memakan waktu lebih lama daripada konstruksi di buku catatan. Menariknya, antara lain, melihat bagaimana lingkungan komputer menjalankan perintah manusia untuk membuat figur pesawat. Berikut adalah Lampiran No. 3, yang menjelaskan langkah-langkah konstruksi Anda secara rinci. Muat program dan buka gambar baru ( geser nomor 8, 9).

    Gambarlah objek geometris yang ditentukan dalam rumusan masalah: sinar A dimulai dari suatu titik A dan segmennya sama M– panjang sewenang-wenang ( geser nomor 10).

    Masukkan penunjukan sinar, ruas, awal sinar pada gambar menggunakan tab "Peralatan" teks.

    Buatlah sebuah lingkaran dengan jari-jari sama dengan segmennya M berpusat di titik sudut pada suatu titik tertentu A (geser nomor 11).

    M dengan pusat di titik sudut diberikan titik A ( geser nomor 12, 13).

    Buatlah sebuah lingkaran dengan jari-jari sama dengan segmen lebih besar dari 1/2 M Untuk melakukan ini, pilih item “ di menu konteks RMB Antara 2 poin" (geser nomor 14, 15, 16).

    Melalui titik potong lingkaran M dan N menggambar garis lurus ( geser nomor 17,18).

    Buku Bekas:

    1. Ugrinovich N.D. “Informatika. Kursus dasar" kelas 7. - M.: BINOM – 2008 – 175 hal.
    2. Ugrinovich N.D. “Lokakarya tentang ilmu komputer dan teknologi Informasi" tutorial. – M.: BINOM, 2004-2006. -
    3. Ugrinovich N.D. “Mengajar mata kuliah “Informatika dan TIK” di sekolah dasar dan menengah atas kelas 8-11 M.: BINOM Laboratory of Knowledge, 2008. - 180 hal.
    4. Ugrinovich N.D. Lokakarya komputer dalam CD-ROM. – M.: BINOM, 2004-2006.
    5. Boguslavsky A.A., Tretyak T.M. Farafonov A.A. “Kompas - 3D v 5.11-8.0 Workshop untuk pemula” - M.: SOLON - PRESS, 2006 - 272 hal.
    6. Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., dkk. “Geometri 7-9. Buku teks untuk sekolah menengah” – M: Pendidikan 2006 – 384 hal.
    7. Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., dkk “Studi geometri kelas 7-9. Rekomendasi metodologis untuk buku teks” - M: Education 1997 - 255 hal.
    8. Afanasyeva T.L., Tapilina L.A. “Rencana pembelajaran berdasarkan buku teks kelas 8 karya Atanasyan L.S.” - Volgograd “Guru” 2010, 166 hal.

    Lampiran No.1

    Rencanakan penyelesaian masalah yang melibatkan konstruksi dengan kompas dan penggaris.

    1. Analisis.
    2. Konstruksi.
    3. Bukti.
    4. Belajar.

    Penjelasan

    1. Saat melakukan analisis, gambar yang diinginkan digambar secara skematis dan hubungan dibuat antara data tugas dan elemen yang diperlukan.
    2. Sesuai rencana, pembangunan dilakukan dengan menggunakan kompas dan penggaris.
    3. Mereka membuktikan bahwa angka yang dibangun memenuhi kondisi permasalahan.
    4. Mereka melakukan penelitian: apakah permasalahan mempunyai solusi untuk data tertentu, dan jika ya, berapa banyak solusi?

    Contoh soal konstruksi dasar

    1. Sisihkan segmen yang sama dengan segmen yang diberikan.
    2. Buatlah garis bagi yang tegak lurus terhadap segmen tersebut.
    3. Buatlah titik tengah segmen tersebut.
    4. Buatlah sebuah garis yang melalui suatu titik tertentu, tegak lurus terhadap suatu garis tertentu (Titik tersebut mungkin terletak atau tidak terletak pada suatu garis tertentu).
    5. Buatlah garis bagi sudut tersebut.
    6. Buatlah sudut yang sama dengan sudut yang diberikan.

    Lampiran No.2

    Tempat kedudukan titik-titik geometri (GLP) adalah himpunan titik-titik yang mempunyai sifat tertentu.

    Contoh GMT:

    1. Garis bagi yang tegak lurus suatu ruas adalah himpunan titik-titik yang berjarak sama dari ujung-ujung ruas tersebut.
    2. Lingkaran adalah himpunan titik-titik yang berjarak sama titik tertentu– pusat lingkaran.
    3. Garis bagi suatu sudut adalah himpunan titik-titik yang berjarak sama terhadap sisi-sisi sudut.

    Setiap titik pada garis bagi suatu segmen mempunyai jarak yang sama dari ujung-ujung segmen tersebut.

      Glosarium istilah planimetri- Definisi istilah dari planimetri dikumpulkan di sini. Referensi istilah-istilah dalam glosarium ini (di halaman ini) dicetak miring. # A B C D E E E F G H I J K L M N O P R S ... Wikipedia

      Poin-poin yang kolinear

      Langsung kompetitif- Definisi istilah dari planimetri dikumpulkan di sini. Referensi istilah-istilah dalam glosarium ini (di halaman ini) dicetak miring. # A B C D E E F G H I J K L M N O P R S T U V ... Wikipedia

      Lingkaran Apollonia- Definisi istilah dari planimetri dikumpulkan di sini. Referensi istilah-istilah dalam glosarium ini (di halaman ini) dicetak miring. # A B C D E E F G H I J K L M N O P R S T U V ... Wikipedia

      Transformasi pesawat- Definisi istilah dari planimetri dikumpulkan di sini. Referensi istilah-istilah dalam glosarium ini (di halaman ini) dicetak miring. # A B C D E E F G H I J K L M N O P R S T U V ... Wikipedia

      Ceviana- Definisi istilah dari planimetri dikumpulkan di sini. Referensi istilah-istilah dalam glosarium ini (di halaman ini) dicetak miring. # A B C D E E F G H I J K L M N O P R S T U V ... Wikipedia

      Glosarium planimetri- Halaman ini adalah glosarium. Lihat juga artikel utama : Planimetri Definisi istilah dari planimetri dikumpulkan di sini. Tautan ke istilah-istilah dalam kamus ini (di halaman ini) dicetak miring... Wikipedia

      masalah Apollonius- Masalah Apollonius adalah membuat lingkaran yang bersinggungan dengan tiga lingkaran tertentu menggunakan kompas dan penggaris. Menurut legenda, masalah tersebut dirumuskan oleh Apollonius dari Perga sekitar tahun 220 SM. e. dalam buku "Touch", yang hilang ... Wikipedia

      masalah Apollonius- Masalah Apollonius adalah membuat lingkaran yang bersinggungan dengan tiga lingkaran tertentu menggunakan kompas dan penggaris. Menurut legenda, masalah tersebut dirumuskan oleh Apollonius dari Perga sekitar tahun 220 SM. e. dalam buku "Menyentuh", yang hilang, tapi... ... Wikipedia

      Diagram gagak- himpunan titik-titik acak pada bidang Diagram Voronoi dari himpunan titik-titik S yang terbatas pada bidang mewakili partisi bidang sedemikian rupa sehingga ... Wikipedia

    Pada pelajaran sebelumnya, kita telah mempelajari sifat-sifat garis bagi suatu sudut, baik yang tertutup segitiga maupun bebas. Sebuah segitiga mencakup tiga sudut dan untuk masing-masing sudut tersebut sifat-sifat garis bagi yang dipertimbangkan dipertahankan.

    Dalil:

    Garis bagi AA 1, BB 1, СС 1 dari segitiga berpotongan di satu titik O (Gbr. 1).

    Beras. 1. Ilustrasi teorema

    Bukti:

    Mari kita perhatikan dulu dua garis bagi BB 1 dan CC 1. Mereka berpotongan, titik potong O ada. Untuk membuktikannya, mari kita asumsikan kebalikannya: misalkan garis-bagi yang diberikan tidak berpotongan, dalam hal ini garis-garis tersebut sejajar. Maka garis lurus BC adalah garis potong dan jumlah sudutnya adalah , hal ini bertentangan dengan fakta bahwa pada seluruh segitiga jumlah sudutnya adalah .

    Jadi, titik O pada perpotongan dua garis bagi ada. Mari kita pertimbangkan propertinya:

    Titik O terletak pada garis bagi sudut, artinya berjarak sama terhadap sisi BA dan BC. Jika OK tegak lurus BC, OL tegak lurus BA, maka panjang tegak lurus tersebut sama dengan - . Selain itu, titik O terletak pada garis bagi sudut dan berjarak sama dari sisinya CB dan CA, garis tegak lurus OM dan OK adalah sama.

    Kami memperoleh persamaan berikut:

    , yaitu ketiga garis tegak lurus yang dijatuhkan dari titik O ke sisi-sisi segitiga adalah sama besar.

    Kami tertarik pada persamaan garis tegak lurus OL dan OM. Persamaan ini menyatakan bahwa titik O berjarak sama terhadap sisi-sisi sudut, sehingga terletak pada garis bagi AA 1.

    Jadi, kita telah membuktikan bahwa ketiga garis bagi suatu segitiga berpotongan di satu titik.

    Selain itu, segitiga terdiri dari tiga ruas, yang berarti kita harus mempertimbangkan sifat-sifat masing-masing ruas.

    Segmen AB diberikan. Setiap segmen mempunyai titik tengah, dan garis tegak lurus dapat ditarik melaluinya - mari kita nyatakan sebagai p. Jadi, p adalah garis bagi yang tegak lurus.

    Beras. 2. Ilustrasi teorema

    Setiap titik yang terletak pada garis bagi yang tegak lurus mempunyai jarak yang sama dari ujung-ujung ruas tersebut.

    Buktikan itu (Gbr. 2).

    Bukti:

    Perhatikan segitiga dan . Mereka berbentuk persegi panjang dan sama besar, karena mereka memiliki kaki yang sama OM, dan kaki AO dan OB sama syaratnya, jadi kita punya dua segitiga siku-siku, sama dengan dua kaki. Oleh karena itu, sisi miring segitiga juga sama, yaitu hal yang perlu dibuktikan.

    Teorema kebalikannya benar.

    Setiap titik yang berjarak sama dari ujung suatu ruas terletak pada garis bagi yang tegak lurus ruas tersebut.

    Diketahui sebuah ruas AB, garis bagi yang tegak lurus p, dan sebuah titik M yang berjarak sama dari ujung-ujung ruas tersebut. Buktikan bahwa titik M terletak pada garis bagi yang tegak lurus terhadap ruas tersebut (Gbr. 3).

    Beras. 3. Ilustrasi teorema

    Bukti:

    Pertimbangkan sebuah segitiga. Bentuknya sama kaki, sesuai kondisinya. Perhatikan median suatu segitiga: titik O adalah titik tengah alas AB, OM adalah mediannya. Menurut properti segitiga sama kaki, median yang ditarik ke alasnya adalah tinggi dan garis bagi. Oleh karena itu. Namun garis p juga tegak lurus AB. Kita mengetahui bahwa di titik O dapat ditarik satu garis tegak lurus terhadap ruas AB, yang berarti garis OM dan p berhimpitan, maka titik M termasuk dalam garis lurus p, yang perlu kita buktikan.

    Langsung dan kebalikan dari teorema dapat digeneralisasikan.

    Suatu titik terletak pada garis bagi yang tegak lurus suatu ruas jika dan hanya jika titik tersebut berjarak sama dari ujung-ujung ruas tersebut.

    Jadi, mari kita ulangi bahwa ada tiga segmen dalam sebuah segitiga dan sifat garis bagi yang tegak lurus berlaku untuk masing-masing segmen tersebut.

    Dalil:

    Garis-bagi yang tegak lurus suatu segitiga berpotongan di satu titik.

    Sebuah segitiga diberikan. Tegak lurus terhadap sisi-sisinya: P 1 ke sisi BC, P 2 ke sisi AC, P 3 ke sisi AB.

    Buktikan bahwa garis tegak lurus P 1, P 2 dan P 3 berpotongan di titik O (Gbr. 4).

    Beras. 4. Ilustrasi teorema

    Bukti:

    Mari kita perhatikan dua garis bagi yang tegak lurus P 2 dan P 3, keduanya berpotongan, titik potong O ada. Mari kita buktikan fakta ini dengan kontradiksi - misalkan garis tegak lurus P 2 dan P 3 sejajar. Kemudian sudutnya dibalik, yang bertentangan dengan fakta bahwa jumlah ketiga sudut suatu segitiga adalah . Jadi, terdapat titik O pada perpotongan dua dari tiga garis bagi yang tegak lurus. Sifat-sifat titik O: terletak pada garis bagi yang tegak lurus terhadap sisi AB, yang berarti berjarak sama dari ujung-ujung ruas AB: . Ia juga terletak pada garis bagi yang tegak lurus terhadap sisi AC, yang artinya . Kami memperoleh persamaan berikut.

    Pada pelajaran sebelumnya, kita telah mempelajari sifat-sifat garis bagi suatu sudut, baik yang tertutup segitiga maupun bebas. Sebuah segitiga mencakup tiga sudut dan untuk masing-masing sudut tersebut sifat-sifat garis bagi yang dipertimbangkan dipertahankan.

    Dalil:

    Garis bagi AA 1, BB 1, СС 1 dari segitiga berpotongan di satu titik O (Gbr. 1).

    Beras. 1. Ilustrasi teorema

    Bukti:

    Mari kita perhatikan dulu dua garis bagi BB 1 dan CC 1. Mereka berpotongan, titik potong O ada. Untuk membuktikannya, mari kita asumsikan kebalikannya: misalkan garis-bagi yang diberikan tidak berpotongan, dalam hal ini garis-garis tersebut sejajar. Maka garis lurus BC adalah garis potong dan jumlah sudutnya adalah , hal ini bertentangan dengan fakta bahwa pada seluruh segitiga jumlah sudutnya adalah .

    Jadi, titik O pada perpotongan dua garis bagi ada. Mari kita pertimbangkan propertinya:

    Titik O terletak pada garis bagi sudut, artinya berjarak sama terhadap sisi BA dan BC. Jika OK tegak lurus BC, OL tegak lurus BA, maka panjang tegak lurus tersebut sama dengan - . Selain itu, titik O terletak pada garis bagi sudut dan berjarak sama dari sisinya CB dan CA, garis tegak lurus OM dan OK adalah sama.

    Kami memperoleh persamaan berikut:

    , yaitu ketiga garis tegak lurus yang dijatuhkan dari titik O ke sisi-sisi segitiga adalah sama besar.

    Kami tertarik pada persamaan garis tegak lurus OL dan OM. Persamaan ini menyatakan bahwa titik O berjarak sama terhadap sisi-sisi sudut, sehingga terletak pada garis bagi AA 1.

    Jadi, kita telah membuktikan bahwa ketiga garis bagi suatu segitiga berpotongan di satu titik.

    Selain itu, segitiga terdiri dari tiga ruas, yang berarti kita harus mempertimbangkan sifat-sifat masing-masing ruas.

    Segmen AB diberikan. Setiap segmen mempunyai titik tengah, dan garis tegak lurus dapat ditarik melaluinya - mari kita nyatakan sebagai p. Jadi, p adalah garis bagi yang tegak lurus.

    Beras. 2. Ilustrasi teorema

    Setiap titik yang terletak pada garis bagi yang tegak lurus mempunyai jarak yang sama dari ujung-ujung ruas tersebut.

    Buktikan itu (Gbr. 2).

    Bukti:

    Perhatikan segitiga dan . Bentuknya persegi panjang dan sama besar, karena keduanya mempunyai kaki yang sama OM, dan kaki AO dan OB sama syaratnya, jadi kita mempunyai dua segitiga siku-siku, yang kedua kakinya sama besar. Oleh karena itu, sisi miring segitiga juga sama, yaitu hal yang perlu dibuktikan.

    Teorema kebalikannya benar.

    Setiap titik yang berjarak sama dari ujung suatu ruas terletak pada garis bagi yang tegak lurus ruas tersebut.

    Diketahui sebuah ruas AB, garis bagi yang tegak lurus p, dan sebuah titik M yang berjarak sama dari ujung-ujung ruas tersebut. Buktikan bahwa titik M terletak pada garis bagi yang tegak lurus terhadap ruas tersebut (Gbr. 3).

    Beras. 3. Ilustrasi teorema

    Bukti:

    Pertimbangkan sebuah segitiga. Bentuknya sama kaki, sesuai kondisinya. Perhatikan median suatu segitiga: titik O adalah titik tengah alas AB, OM adalah mediannya. Berdasarkan sifat segitiga sama kaki, median yang ditarik ke alasnya adalah tinggi dan garis bagi. Oleh karena itu. Namun garis p juga tegak lurus AB. Kita mengetahui bahwa di titik O dapat ditarik satu garis tegak lurus terhadap ruas AB, yang berarti garis OM dan p berhimpitan, maka titik M termasuk dalam garis lurus p, yang perlu kita buktikan.

    Teorema langsung dan teorema kebalikannya dapat digeneralisasikan.

    Suatu titik terletak pada garis bagi yang tegak lurus suatu ruas jika dan hanya jika titik tersebut berjarak sama dari ujung-ujung ruas tersebut.

    Jadi, mari kita ulangi bahwa ada tiga segmen dalam sebuah segitiga dan sifat garis bagi yang tegak lurus berlaku untuk masing-masing segmen tersebut.

    Dalil:

    Garis-bagi yang tegak lurus suatu segitiga berpotongan di satu titik.

    Sebuah segitiga diberikan. Tegak lurus terhadap sisi-sisinya: P 1 ke sisi BC, P 2 ke sisi AC, P 3 ke sisi AB.

    Buktikan bahwa garis tegak lurus P 1, P 2 dan P 3 berpotongan di titik O (Gbr. 4).

    Beras. 4. Ilustrasi teorema

    Bukti:

    Mari kita perhatikan dua garis bagi yang tegak lurus P 2 dan P 3, keduanya berpotongan, titik potong O ada. Mari kita buktikan fakta ini dengan kontradiksi - misalkan garis tegak lurus P 2 dan P 3 sejajar. Kemudian sudutnya dibalik, yang bertentangan dengan fakta bahwa jumlah ketiga sudut suatu segitiga adalah . Jadi, terdapat titik O pada perpotongan dua dari tiga garis bagi yang tegak lurus. Sifat-sifat titik O: terletak pada garis bagi yang tegak lurus terhadap sisi AB, yang berarti berjarak sama dari ujung-ujung ruas AB: . Ia juga terletak pada garis bagi yang tegak lurus terhadap sisi AC, yang artinya . Kami memperoleh persamaan berikut.

    Garis bagi tegak lurus (tegak lurus median atau perantara wanita) - garis lurus yang tegak lurus terhadap suatu segmen tertentu dan melalui titik tengahnya.

    Properti

    p_a=\tfrac(2aS)(a^2+b^2-c^2), p_b=\tfrac(2bS)(a^2+b^2-c^2), p_c=\tfrac(2cS)( a^2-b^2+c^2), di mana subskrip menunjukkan sisi di mana garis tegak lurus digambar, S adalah luas segitiga, dan diasumsikan juga bahwa sisi-sisinya dihubungkan oleh pertidaksamaan a\geqslant b\geqslant c. p_a\geq p_b Dan p_c\geq p_b. Dengan kata lain, garis bagi tegak lurus terkecil suatu segitiga termasuk dalam ruas tengah.

    Tulis ulasan tentang artikel "Sektor tegak lurus"

    Catatan

    Kutipan yang mencirikan garis-bagi tegak lurus

    Kutuzov, berhenti untuk mengunyah, menatap Wolzogen dengan heran, seolah tidak mengerti apa yang dikatakan kepadanya. Wolzogen, menyadari kegembiraan des alten Herrn, [pria tua (Jerman)] berkata sambil tersenyum:
    – Saya tidak menganggap diri saya berhak menyembunyikan dari Yang Mulia apa yang saya lihat... Pasukan berada dalam kekacauan total...
    - Sudahkah kau melihat? Apakah kamu melihat?.. – Kutuzov berteriak, mengerutkan kening, segera bangkit dan maju ke arah Wolzogen. “Bagaimana kamu… beraninya kamu!..”, teriaknya sambil membuat gerakan mengancam dengan berjabat tangan dan tersedak. - Beraninya kamu, tuan, mengatakan ini padaku? Anda tidak tahu apa-apa. Beritahu Jenderal Barclay dari saya bahwa informasinya tidak benar dan bahwa jalannya pertempuran yang sebenarnya lebih diketahui oleh saya, Panglima Tertinggi, daripada dia.
    Wolzogen ingin menolak, tapi Kutuzov memotongnya.
    - Musuh dipukul mundur di sisi kiri dan dikalahkan di sayap kanan. Jika Anda belum melihatnya dengan baik, Tuan, jangan biarkan diri Anda mengatakan apa yang tidak Anda ketahui. Silakan menemui Jenderal Barclay dan sampaikan kepadanya keesokan harinya niat mutlak saya untuk menyerang musuh,” kata Kutuzov tegas. Semua orang terdiam, dan yang terdengar hanyalah nafas berat jenderal tua yang kehabisan nafas. “Mereka berhasil dipukul mundur di mana-mana, dan saya berterima kasih kepada Tuhan dan tentara pemberani kami.” Musuh telah dikalahkan, dan besok kami akan mengusirnya dari tanah suci Rusia,” kata Kutuzov sambil membuat tanda salib; dan tiba-tiba terisak karena air mata yang keluar. Wolzogen, mengangkat bahu dan mengerucutkan bibir, diam-diam berjalan ke samping, bertanya-tanya tentang Eingenommenheit des alten Herrn. [pada tirani orang tua ini. (Jerman)]
    “Ya, ini dia, pahlawanku,” kata Kutuzov kepada jenderal gemuk, tampan, berambut hitam, yang saat itu sedang memasuki gundukan itu. Raevsky-lah yang menghabiskan sepanjang hari di titik utama ladang Borodino.
    Raevsky melaporkan bahwa pasukan sudah kokoh di tempatnya dan Prancis tidak berani menyerang lagi. Setelah mendengarkannya, Kutuzov berkata dalam bahasa Prancis:
    – Anda tidak berpikir bagaimana dengan apa yang mengharuskan kita pensiun? [Kalau begitu, kamu tidak berpikir, seperti orang lain, bahwa kita harus mundur?]