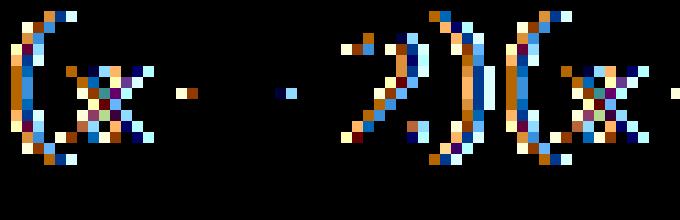Faktorisasi linier beberapa trinomial kuadrat. Memfaktorkan Faktor Linier Polinomial dari Persamaan Kuadrat

Bentuknya persegi dan terdiri dari tiga suku (). Jadi ternyata - trinomial persegi.

Contoh Bukan trinomial persegi:

\(x^3-3x^2-5x+6\) - segi empat kubik
\(2x+1\) - binomial linier

Akar kuadrat dari trinomial:

Contoh:
Trinomial \(x^2-2x+1\) mempunyai akar \(1\), karena \(1^2-2 1+1=0\)
Trinomial \(x^2+2x-3\) mempunyai akar \(1\) dan \(-3\), karena \(1^2+2-3=0\) dan \((-3)^ 2-6-3=9-9=0\)

Misalnya: jika Anda perlu mencari akar-akar trinomial kuadrat \(x^2-2x+1\), kita samakan dengan nol dan selesaikan persamaan \(x^2-2x+1=0\).

\(D=4-4\cdot1=0\)
\(x=\frac(2-0)(2)=\frac(2)(2)=1\)

Siap. Akarnya adalah \(1\).

Penguraian trinomial kuadrat menjadi:

Trinomial persegi \(ax^2+bx+c\) dapat diperluas menjadi \(a(x-x_1)(x-x_2)\) jika persamaan \(ax^2+bx+c=0\) adalah lebih besar dari nol \ (x_1\) dan \(x_2\) adalah akar-akar persamaan yang sama).

Misalnya, pertimbangkan trinomial \(3x^2+13x-10\).
kamu persamaan kuadrat Diskriminan \(3x^2+13x-10=0\) adalah 289 (lebih besar dari nol), dan akar-akarnya adalah \(-5\) dan \(\frac(2)(3)\). Oleh karena itu \(3x^2+13x-10=3(x+5)(x-\frac(2)(3))\). Sangat mudah untuk memverifikasi kebenaran pernyataan ini - jika kita , maka kita akan mendapatkan trinomial aslinya.

Trinomial persegi \(ax^2+bx+c\) dapat direpresentasikan sebagai \(a(x-x_1)^2\) jika diskriminan dari persamaan \(ax^2+bx+c=0\) adalah nol.

Misalnya, pertimbangkan trinomial \(x^2+6x+9\).
Persamaan kuadrat \(x^2+6x+9=0\) memiliki diskriminan sama dengan \(0\) dan akar unik sama dengan \(-3\). Artinya \(x^2+6x+9=(x+3)^2\) (di sini koefisiennya adalah \(a=1\), jadi tidak ditulis sebelum tanda kurung - tidak perlu). Harap dicatat bahwa konversi yang sama dapat dilakukan dengan .

Trinomial kuadrat \(ax^2+bx+c\) tidak dapat difaktorkan jika diskriminan persamaan \(ax^2+bx+c=0\) kurang dari nol.

Misalnya, trinomial \(x^2+x+4\) dan \(-5x^2+2x-1\) memiliki diskriminan kurang dari nol. Oleh karena itu, mustahil untuk memfaktorkannya.

Contoh . Faktorkan \(2x^2-11x+12\).
Larutan :
Mari kita cari akar-akar persamaan kuadrat \(2x^2-11x+12=0\)

\(D=11^2-4 \cdot 2 \cdot 12=121-96=25>0\)
\(x_1=\frac(11-5)(4)=1,5;\) \(x_2=\frac(11+5)(4)=4.\)

Jadi, \(2x^2-11x+12=2(x-1.5)(x-4)\)
Menjawab : \(2(x-1.5)(x-4)\)

Jawaban yang dihasilkan mungkin ditulis berbeda: \((2x-3)(x-4)\).

Contoh . (Tugas dari OGE) Trinomial persegi difaktorkan \(5x^2+33x+40=5(x++ 5)(x-a)\). Menemukan sebuah\).
Larutan:
\(5x^2+33x+40=0\)
\(D=33^2-4 \cdot 5 \cdot 40=1089-800=289=17^2\)
\(x_1=\frac(-33-17)(10)=-5\)
\(x_2=\frac(-33+17)(10)=-1,6\)
\(5x^2+33x+40=5(x+5)(x+1,6)\)
Menjawab : \(-1,6\)

Trinomial persegi dapat difaktorkan sebagai berikut:

Ax 2 + bx + c = a ⋅ (x − x 1) ⋅ (x − x 2)

dimana a adalah bilangan, koefisien sebelum koefisien terdepan,

x – variabel (yaitu huruf),

x 1 dan x 2 adalah bilangan-bilangan, akar-akar persamaan kuadrat a x 2 + b x + c = 0, yang dicari melalui diskriminan.

Jika persamaan kuadrat hanya mempunyai satu akar, maka pemuaiannya seperti ini:

ax 2 + bx + c = a ⋅ (x − x 0) 2

Contoh pemfaktoran trinomial kuadrat:

− x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7

− x 2 + 6 x + 7 = (− 1) ⋅ (x − (− 1)) (x − 7) = − (x + 1) (x − 7) = (x + 1) (7 − x)

− x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2

− x 2 + 4 x − 4 = (− 1) ⋅ (x − 2) 2 = − (x − 2) 2

Jika trinomial kuadrat tidak lengkap (b = 0 atau c = 0), maka dapat difaktorkan dengan cara sebagai berikut:

c = 0 ⇒ ax 2 + bx = x (ax + b)

b = 0 ⇒ terapkan rumus perkalian yang disingkat untuk selisih kuadrat.

Tugas untuk solusi mandiri

No.1. Trinomial persegi difaktorkan: x 2 + 6 x − 27 = (x + 9) (x − a) . Menemukan sebuah.

Larutan:

Pertama, Anda perlu menyamakan trinomial kuadrat dengan nol untuk mencari x 1 dan x 2.

x 2 + 6 x − 27 = 0

a = 1, b = 6, c = − 27

D = b 2 − 4 ac = 6 2 − 4 ⋅ 1 ⋅ (− 27) = 36 + 108 = 144

D > 0 berarti akan ada dua akar yang berbeda.

x 1,2 = − b ± D 2 a = − 6 ± 144 2 ⋅ 1 = [ − 6 + 12 2 = 6 2 = 3 − 6 − 12 2 = − 18 2 = − 9

Mengetahui akar-akarnya, kita memfaktorkan trinomial kuadrat:

x 2 + 6 x − 27 = (x − (− 9)) (x − 3) = (x + 9) (x − 3)

No.2. Persamaan x 2 + p x + q = 0 mempunyai akar-akar − 5; 7. Temukan q.

Larutan:

1 cara:(Anda perlu mengetahui cara memfaktorkan trinomial kuadrat)

Jika x 1 dan x 2 adalah akar-akar trinomial kuadrat a x 2 + b x + c, maka dapat difaktorkan sebagai berikut: a x 2 + b x + c = a ⋅ (x − x 1) ⋅ (x − x 2) .

Karena dalam suatu trinomial kuadrat tertentu koefisien utamanya (faktor di depan x 2) sama dengan satu, pemuaiannya adalah sebagai berikut:

x 2 + p x + q = (x − x 1) (x − x 2) = (x − (− 5)) (x − 7) = (x + 5) (x − 7) = x 2 − 7 x + 5 x − 35 = x 2 − 2 x − 35

x 2 + p x + q = x 2 − 2 x − 35 ⇒ p = − 2, q = − 35

Metode 2: (Anda perlu mengetahui teorema Vieta)

Teorema Vieta:

Jumlah akar-akar trinomial kuadrat tereduksi x 2 + p x + q sama dengan koefisien kedua p yang bertanda berlawanan, dan hasil kali adalah anggota bebas Q.

( x 1 + x 2 = − p x 1 ⋅ x 2 = q

q = x 1 ⋅ x 2 = (− 5) ⋅ 7 = − 35.

Pertama-tama, mari kita tunjukkan beberapa nama umum. Mari kita perhatikan polinomial yang hanya berisi satu huruf, misalnya huruf x. Maka yang paling sederhana adalah polinomial yang mempunyai dua suku, salah satunya mengandung huruf x sampai derajat pertama, dan yang lainnya tidak mengandung huruf x sama sekali, misalnya 3x – 5 atau 15 – 7x atau 8z + 7 (di sini alih-alih huruf x diambil huruf z), dst. Polinomial seperti itu disebut binomial linier .

3x² – 5x + 7 atau x² + 2x – 1
atau 5y² + 7y + 8 atau z² – 5z – 2, dst.

Polinomial seperti ini disebut trinomial persegi.

Kemudian kita dapat membentuk segiempat kubik, misalnya:

x³ + 2x² – x + 1 atau 3x³ – 5x² – 2x – 3 dst.,

polinomial derajat keempat, misalnya:

x 4 – 2x³ – 3x² + 4x – 5, dst.

Koefisien di x, di x², di x³, dst juga dapat dilambangkan dengan huruf, misalnya dengan huruf a, b, c, dst.

1) bentuk umum binomial ax + b, linier terhadap x,

2) bentuk umum trinomial kuadrat (relatif terhadap x): ax² + bx + c,

3) bentuk umum trinomial kubik (relatif terhadap x): ax³ + bx² + cx + d, dst.

Dengan mengganti huruf a, b, c, d... dalam rumus ini dengan bilangan yang berbeda, kita mendapatkan semua jenis binomial linier, trinomial persegi, dll. Misalnya, dalam rumus ax² + bx + c, yang menyatakan persamaan umum bentuk trinomial kuadrat, kita ganti huruf a dengan angka + 3, huruf b dengan angka –2 dan huruf dengan angka –1, kita peroleh trinomial persegi 3x² – 2x – 1. Dalam kasus tertentu, binomial juga dapat diperoleh dengan mengganti salah satu huruf dengan nol, misalnya jika a = +1, b = 0 dan c = –3, maka kita mendapatkan binomial kuadrat x² – 3.

Anda dapat belajar memfaktorkan beberapa trinomial kuadrat dengan cukup cepat menjadi faktor linier. Namun, kami akan membatasi diri untuk hanya mempertimbangkan trinomial kuadrat yang memenuhi kondisi berikut:

1) koefisien suku terdepan (untuk x²) adalah +1,

2) Anda dapat menemukan dua bilangan bulat (dengan tanda, atau dua bilangan bulat relatif) sedemikian rupa sehingga jumlahnya sama dengan koefisien x pangkat pertama dan hasil kali keduanya sama dengan suku bebas x (jika tidak ada huruf x di semua).

Contoh. 1.x² + 5x + 6; Sangat mudah untuk secara mental mencari dua bilangan (yang mempunyai tanda) sehingga jumlahnya sama dengan +5 (koefisien x) dan hasil kali keduanya = +6 (suku bebas dari x) - bilangan-bilangan ini adalah: +2 dan + 3 [sebenarnya +2 + 3 = +5 dan (+2) ∙ (+3) = +6]. Dengan menggunakan kedua bilangan tersebut, kita ganti suku +5x dengan dua suku, yaitu: +2x + 3x (tentunya +2x + 3x = +5x); maka suku teknis kita akan diubah secara artifisial menjadi suku empat x² + 2x + 3x + 6. Sekarang mari kita terapkan teknik pengelompokan padanya, dengan memasukkan dua suku pertama ke dalam satu kelompok dan dua suku terakhir ke kelompok lain:

x² + 5x + 6 = x² + 2x + 3x + 6 = x (x + 2) + 3 (x + 2) = (x + 2) (x + 3).

Pada kelompok pertama kita mengeluarkan x dari kurung dan pada kelompok kedua +3, kita mendapatkan dua suku yang memiliki faktor persekutuan (x + 2), yang juga kita keluarkan dari kurung, dan trinomial kita x² + 5x + 6 didekomposisi menjadi 2 faktor linier: x + 2 dan x + 3.

2. x² – x – 12. Di sini Anda perlu mencari dua bilangan (relatif) yang jumlahnya sama dengan –1 dan hasil kali keduanya sama dengan –12. Angka-angka ini adalah: –4 dan +3.

Periksa: –4 + 3 = –1; (–4) (+3) = –12. Dengan menggunakan bilangan-bilangan ini, kita ganti suku –x dengan dua suku: –x = –4x + 3x, – kita peroleh:

x² – x – 12 = x² – 4x + 3x – 12 = x (x – 4) + 3 (x – 4) = (x – 4) (x + 3).

3.x² – 7x + 6; di sini angka yang dibutuhkan adalah: –6 dan –1. [Periksa: –6 + (–1) = –7; (–6) (–1) = +6].

x² – 7x + 6 = x² – 6x – x + 6 = x (x – 6) – (x – 6) = (x – 6) (x – 1).

Di sini anggota kelompok kedua –x + 6 harus diapit tanda kurung, dengan tanda minus di depannya.

4. x² + 8x – 48. Di sini Anda perlu mencari dua bilangan sehingga jumlahnya +8 dan hasil kali –48. Karena hasil perkaliannya harus ada tanda minus, maka bilangan-bilangan yang diminta harus mempunyai tanda yang berbeda-beda, karena jumlah bilangan kita mempunyai tanda +, maka nilai mutlak pasti ada lebih banyak angka positif. Berlangsung bilangan aritmatika 48 dengan dua faktor (dan ini dapat dilakukan dengan cara yang berbeda), kita peroleh: 48 = 1 ∙ 48 = 2 ∙ 24 = 3 ∙ 16 = 4 ∙ 12 = 6 ∙ 8. Dari perluasan tersebut mudah untuk memilih salah satu yang sesuai dengan syarat kita yaitu : 48 = 4 ∙ 12. Maka bilangan kita adalah : +12 dan –4. Selebihnya sederhana:

x² + 8x – 48 = x² + 12x – 4x – 48 = x (x + 12) – 4 (x + 12) = (x + 12) (x – 4).

5. x² + 7x – 12. Di sini Anda perlu mencari 2 bilangan sehingga jumlahnya +7 dan hasil kali = –12; 12 = 1 ∙ 12 = 2 ∙ 6 = 3 ∙ 4. Rupanya, 3 dan 4 adalah bilangan yang cocok, tetapi keduanya harus diambil dengan tanda yang berbeda agar hasil kali keduanya sama dengan –12, dan jumlah keduanya tidak boleh menjadi +7 [–3 + (+4) = +1, +3 + (–4) = –1]. Faktorisasi lain juga tidak memberikan angka yang dibutuhkan; Oleh karena itu, kami sampai pada kesimpulan bahwa kami belum dapat menguraikan trinomial kuadrat ini menjadi faktor linier, karena teknik kami tidak dapat diterapkan padanya (tidak memenuhi kondisi kedua yang ditetapkan di awal).

Dalam pelajaran ini kita akan mempelajari cara memfaktorkan trinomial kuadrat menjadi faktor linier. Untuk melakukan ini, kita perlu mengingat teorema Vieta dan kebalikannya. Keterampilan ini akan membantu kita dengan cepat dan mudah memperluas trinomial kuadrat menjadi faktor linier, dan juga akan menyederhanakan pengurangan pecahan yang terdiri dari ekspresi.

Jadi mari kita kembali ke persamaan kuadrat, dimana .

Apa yang kita miliki di sisi kiri disebut trinomial kuadrat.

Teorema ini benar: Jika merupakan akar-akar trinomial kuadrat, maka identitasnya berlaku

Dimana adalah koefisien terdepan, adalah akar persamaannya.

Jadi, kita memiliki persamaan kuadrat - trinomial kuadrat, di mana akar-akar persamaan kuadrat disebut juga akar-akar trinomial kuadrat. Oleh karena itu, jika kita mempunyai akar-akar suatu trinomial persegi, maka trinomial tersebut dapat diuraikan menjadi faktor-faktor linier.

Bukti:

Bukti fakta ini dilakukan dengan menggunakan teorema Vieta, yang telah kita bahas pada pelajaran sebelumnya.

Mari kita ingat apa yang dikatakan teorema Vieta kepada kita:

Jika adalah akar-akar trinomial kuadrat yang , maka .

Pernyataan berikut mengikuti teorema ini:

Kita melihat bahwa, menurut teorema Vieta, yaitu dengan mensubstitusi nilai-nilai ini ke dalam rumus di atas, kita memperoleh ekspresi berikut

Q.E.D.

Ingatlah bahwa kita telah membuktikan teorema bahwa jika merupakan akar-akar trinomial persegi, maka pemuaiannya valid.

Sekarang mari kita ingat contoh persamaan kuadrat, yang akar-akarnya kita pilih menggunakan teorema Vieta. Dari fakta ini kita dapat memperoleh persamaan berikut berkat teorema yang terbukti:

Sekarang mari kita periksa kebenaran fakta ini hanya dengan membuka tanda kurung:

Kita melihat bahwa kita memfaktorkan dengan benar, dan setiap trinomial, jika memiliki akar, dapat difaktorkan menurut teorema ini menjadi faktor linier sesuai dengan rumus

Namun, mari kita periksa apakah faktorisasi seperti itu mungkin dilakukan untuk persamaan apa pun:

Ambil contoh persamaan. Pertama, mari kita periksa tanda diskriminannya

Dan kita ingat bahwa untuk memenuhi teorema yang kita pelajari, D harus lebih besar dari 0, jadi dalam hal ini faktorisasi menurut teorema yang kita pelajari tidak mungkin dilakukan.

Oleh karena itu, kita merumuskan teorema baru: jika suatu trinomial persegi tidak mempunyai akar, maka trinomial tersebut tidak dapat diuraikan menjadi faktor linier.

Jadi, kita telah melihat teorema Vieta, kemungkinan penguraian trinomial kuadrat menjadi faktor linier, dan sekarang kita akan menyelesaikan beberapa masalah.

Tugas No.1

Dalam kelompok ini kita akan menyelesaikan masalah yang berbanding terbalik dengan masalah yang diajukan. Kami mempunyai persamaan, dan kami menemukan akar-akarnya dengan memfaktorkannya. Di sini kita akan melakukan yang sebaliknya. Katakanlah kita mempunyai akar-akar persamaan kuadrat

Soal kebalikannya adalah ini: tuliskan persamaan kuadrat menggunakan akar-akarnya.

Ada 2 cara untuk mengatasi masalah ini.

Karena adalah akar-akar persamaannya, maka adalah persamaan kuadrat yang akar-akarnya diberi bilangan. Sekarang mari kita buka tanda kurung dan periksa:

Ini adalah cara pertama kami membuat persamaan kuadrat akar yang diberikan, yang tidak mempunyai akar-akar lain, karena setiap persamaan kuadrat mempunyai paling banyak dua akar.

Metode ini melibatkan penggunaan teorema kebalikan Vietnam.

Jika merupakan akar-akar persamaan, maka akar-akar tersebut memenuhi syarat bahwa .

Untuk persamaan kuadrat tereduksi , , yaitu dalam hal ini, dan .

Jadi, kami telah membuat persamaan kuadrat yang memiliki akar-akar tertentu.

Tugas No.2

Hal ini diperlukan untuk mengurangi pecahan.

Kita mempunyai trinomial pada pembilangnya dan trinomial pada penyebutnya, dan trinomial-trinomial tersebut dapat difaktorkan atau tidak. Jika pembilang dan penyebutnya difaktorkan, maka diantara keduanya ada faktor sama yang dapat dikurangi.

Pertama-tama, Anda perlu memfaktorkan pembilangnya.

Pertama, Anda perlu memeriksa apakah persamaan ini dapat difaktorkan, cari diskriminannya. Karena , tandanya bergantung pada hasil kali (harus kurang dari 0), in dalam contoh ini, yaitu persamaan yang diberikan memiliki akar.

Untuk menyelesaikannya, kami menggunakan teorema Vieta:

Dalam hal ini, karena kita berurusan dengan akar, akan sangat sulit untuk memilih akarnya saja. Namun kita melihat bahwa koefisien-koefisiennya seimbang, yaitu jika kita berasumsi bahwa , dan mensubstitusikan nilai ini ke dalam persamaan, kita mendapatkan sistem berikut: , yaitu 5-5=0. Jadi, kami telah memilih salah satu akar persamaan kuadrat ini.

Kita akan mencari akar kedua dengan mensubstitusikan apa yang sudah diketahui ke dalam sistem persamaan, misalnya, , yaitu. .

Jadi, kami telah menemukan kedua akar persamaan kuadrat dan dapat mensubstitusikan nilainya ke dalam persamaan asli untuk memfaktorkannya:

Mari kita ingat soal awal, kita perlu mengurangi pecahan.

Mari kita coba selesaikan masalah tersebut dengan melakukan substitusi.

Perlu diingat bahwa dalam hal ini penyebutnya tidak boleh sama dengan 0, yaitu , .

Jika kondisi ini terpenuhi, maka pecahan aslinya telah direduksi menjadi bentuk .

Soal No. 3 (tugas dengan parameter)

Berapa nilai parameter jumlah akar persamaan kuadrat

Jika akar persamaan ini ada, maka , pertanyaan: kapan.

TIGA KOTAK III

§ 54. Penguraian trinomial kuadrat menjadi faktor linier

Pada bagian ini kita akan membahas pertanyaan berikut: dalam hal apa trinomial kuadrat itu kapak 2 + bx+c dapat direpresentasikan sebagai sebuah produk

(A 1 x+b 1) (A 2 x+b 2)

dua relatif linier X pengganda dengan koefisien nyata A 1 , B 1 , A 2 , B 2 (A 1 =/=0, A 2 =/=0) ?

1. Misalkan trinomial kuadrat diberikan kapak 2 + bx+c mari kita nyatakan dalam bentuk

kapak 2 + bx+c = (A 1 x+b 1) (A 2 x+b 2). (1)

Ruas kanan rumus (1) hilang ketika X = - B 1 / A 1 dan X = - B 2 / A 2 (A 1 dan A 2 tidak sama dengan nol dengan syarat). Namun dalam hal ini jumlahnya adalah B 1 / A 1 dan - B 2 / A 2 adalah akar persamaan

kapak 2 + bx+c = 0.

Oleh karena itu, diskriminan dari trinomial kuadrat kapak 2 + bx+c harus non-negatif.

2. Sebaliknya, anggaplah diskriminan D = B 2 - 4ac trinomial kuadrat kapak 2 + bx+c non-negatif. Maka trinomial ini mempunyai akar real X 1 dan X 2. Dengan menggunakan teorema Vieta, kita memperoleh:

kapak 2 + bx+c =A (X 2 + B / A X + C / A ) = A [X 2 - (X 1 + X 2) X + X 1 X 2 ] =

= A [(X 2 - X 1 X ) - (X 2 X - X 1 X 2)] = A [X (X - X 1) - X 2 (X - X 1) =

=A (X - X 1)(X - X 2).

kapak 2 + bx+c = A (X - X 1)(X - X 2), (2)

Di mana X 1 dan X 2 - akar trinomial kapak 2 + bx+c . Koefisien A dapat dikaitkan dengan salah satu dari dua faktor linier, misalnya,

A (X - X 1)(X - X 2) = (ah - kapak 1)(X - X 2).

Tetapi ini berarti bahwa dalam kasus ini adalah trinomial persegi kapak 2 + bx+c menyatakannya sebagai produk dari dua faktor linier dengan koefisien nyata.

Menggabungkan hasil yang diperoleh pada paragraf 1 dan 2, kita sampai pada teorema berikut.

Dalil. Trinomial persegi kapak 2 + bx+c kemudian dan hanya kemudian dapat direpresentasikan sebagai produk dari dua faktor linier dengan koefisien nyata,

kapak 2 + bx+c = (ah - kapak 1)(X - X 2),

ketika diskriminan dari trinomial kuadrat ini adalah non-negatif (yaitu, ketika trinomial ini mempunyai akar real).

Contoh 1. Faktorisasi linier 6 X 2 - X -1.

Akar-akar trinomial kuadrat ini adalah sama X 1 = 1/2 dan X 2 = - 1 / 3 .

Oleh karena itu, menurut rumus (2)

6X 2 - X -1 = 6 (X - 1 / 2)(X + 1 / 3) = (2X - 1) (3X + 1).

Contoh 2. Faktorisasi linier X 2 + X + 1. Diskriminan trinomial kuadrat ini negatif:

D = 1 2 - 4 1 1 = - 3< 0.

Oleh karena itu, trinomial kuadrat ini tidak dapat diperluas menjadi faktor linier dengan koefisien riil.

Latihan

Faktorkan persamaan berikut menjadi faktor linier (No. 403 - 406):

403. 6X 2 - 7X + 2. 405. X 2 - X + 1.