1. Первые два признака равенства прямоугольных треугольников.
Для равенства двух треугольников достаточно, чтобы три элемента одного треугольника были равны соответствующим элементам другого треугольника, при этом непременно в число этих элементов должна входить хотя бы одна сторона.
Так как все прямые углы равны между собой, то прямоугольные треугольники уже имеют по одному равному элементу, именно по одному прямому углу.

Отсюда следует, что прямоугольные треугольники равны:
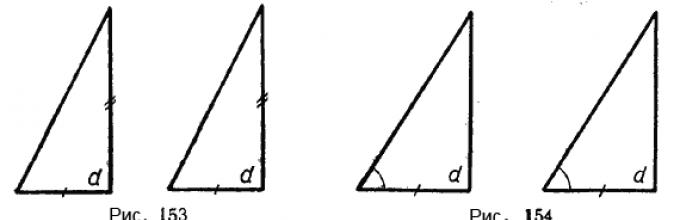
если катеты одного треугольника соответственно равны катетам другого треугольника (рис. 153);
если катет и прилежащий острый угол одного угольника соответственно равны катету и прилежащему острому углу другого треугольника (рис. 154).
Докажем теперь две теоремы, устанавливающие ещё два признака равенства прямоугольных треугольников.
Теоремы о признаках равенства прямоугольных треугольников
Теорема 1. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе иострому углу другого треугольника, то такие прямоугольные треугольники равны.Чтобы доказать эту теорему, построим два прямоугольных гольника ABC и А’В’С’, у которых углы А и А’ равны, гипотенузы АВ и А’В’ также равны, а углы С и С’ - прямые (рис. 157).

Наложим треугольник А’В’С’на треугольник ABC так, чтобы вершина А’ совпала с вершиной А, гипотенуза А’В’ - с равной гипотенузой АВ. Тогда вследствие равенства углов A и А’ катет А’С’ пойдёт по катету АС; катет В’С’ совместится с катетом ВС: оба они - перпендикуляры, проведённые к одной прямой АС из одной точки В. Значит, вершины С и С’ совместятся.
Треугольник ABC совместился с треугольником А’В’С’.
Следовательно, \(\Delta\)АВС = \(\Delta\)А’В’С’.
Эта теорема даёт 3-й признак равенства прямоугольных треугольников (по гипотенузе и острому углу).
Теорема 2. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
Чтобы доказать это, построим два прямоугольных треугольника АВС и А’В’С’, у которых углы С и С’ - прямые, катеты АС и A’C’ равны, гипотенузы АВ и А’В’ также равны (рис. 158).

Проведём прямую MN и отметим на ней точку С, из этой точки проведём перпендикуляр СК к прямой MN. Затем прямой угол треугольника ABC наложим на прямой угол КСМ так, чтобы вершины их совместились и катет АС пошёл по лучу СК, тогда катет ВС пойдёт по лучу СМ. Прямой угол треугольника А’В’С’ наложим на прямой угол KCN так, чтобы вершины их совместились и катет А’С’ пошёл по лучу СК, тогда катет С’В’ пойдёт по лучу CN. Вершины А и А’ совпадут вследствие равенства катетов АС и А’С’.
Треугольники АВС и А’В’С’ составят вместе равнобедренный треугольник ВАВ’, в котором АС окажется высотой и биссектрисой, а значит и осью симметрии треугольника ВАВ’. Из этого следует, что \(\Delta\)АВС = \(\Delta\)А’В’С’.
Эта теорема дает 4-й признак равенства прямоугольных треугольников (по гипотенузе и катету).
Итак, все признаки равенства прямоугольных треугольников:
1. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
3. Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
4. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
5. Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие прямоугольные треугольники равны
Чтобы установить равенство прямоугольных треугольников, достаточно знать, что два элемента одного треугольника соответственно равны двум элементам другого треугольника (исключая прямой угол). Это, конечно, не распространяется на равенство двух углов одного треугольника двум углам другого треугольника.
Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует:
Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис 5).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого треугольника, то такие треугольники равны (рис. 6).

Рассмотрим ещё два признака равенства прямоугольных треугольников.

ТЕОРЕМА . Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого треугольника, то такие треугольники равны (рис. 7).
ДОКАЗАТЕЛЬСТВО. Из свойства 1є § следует, что в таких треугольниках два других острых угла тоже равны, поэтому треугольники равны по второму признаку равенства треугольников, то есть по стороне (гипотенузе) и двум прилежащим углам.
Что и требовалось доказать.
ТЕОРЕМА . Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.
ДОКАЗАТЕЛЬСТВО. Рассмотрим треугольники ABC и A 1 B 1 C 1 , у которых углы C и C 1 - прямые, AB =A 1 B 1 , BC = B 1 C 1 (рис. 8).

Так как < C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с острым углом B 1 A 1 C 1). Но это невозможно, поэтому вершины A и A 1 совместятся. Следовательно, полностью совместятся треугольники ABC A 1 B 1 C 1 , то есть они равны.
Что и требовалось доказать.
Теорема Пифагора
Значение её состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Одна из теорем позволяет убедиться в том, что если из точки вне прямой проведены к ней перпендикуляр и наклонные, то: а) наклонные равны, если равны их проекции; б) та наклонная больше, которая имеет большую проекцию.
Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников. Потом узнали, как находить длины сторон и углы остроугольных и тупоугольных треугольников. Возникла целая наука тригонометрия («тригон» - по-гречески означает «треугольник»). Эта наука нашла применение в землемерии. Но еще раньше с ее помощью научились измерять воображаемые треугольники на небе, вершинами которых были звезды. Сейчас тригонометрию применяют даже для измерения расстояний между космическими кораблями.
Пользуясь свойствами площадей многоугольников, мы установим теперь замечательное соотношение между гипотенузой и катетами прямоугольного треугольника. Теорема, которую мы докажем, называется теоремой Пифагора, которая является важнейшей теоремой геометрии.
Если дан нам треугольник,
И при том с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путем
К результату мы придем.
ТЕОРЕМА. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
ДОКАЗАТЕЛЬСТВО. Рассмотрим прямоугольный треугольник с катетами a, b и c (рис. 9 а).

Докажем, что c 2 = a 2 + b 2 . Достроим треугольник до квадрата со стороной a+b, так как показано на рисунке (рис. 9 б).
Площадь такого квадрата со стороной a + b равна (a + b) 2 . С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь которых равна ab, и квадрат со стороной с, поэтому
Таким образом, (a + b) 2 =2ab + c 2 , откуда c 2 = a 2 + b 2 .
Что и требовалось доказать.
СЛЕДСТВИЕ 1 . В прямоугольном треугольнике любой из катетов меньше гипотенузы.
ДОКАЗАТЕЛЬСТВО. По теореме Пифагора АВ 2 = АС 2 + ВС 2 . Так как ВС 2 >0, то АС 2 <АВ, То есть АС<АВ.
СЛЕДСТВИЕ 2. Для любого острого угла б cosб <1.
ДОКЗАТЕЛЬСВО. По определению косинуса cosб = . Но в следствии 1 было доказано, что АС<АВ, значит, дробь меньше 1.
Прямоугольные треугольники, у которых стороны выражаются целыми числами, называются пифагоровыми треугольниками.
Можно доказать, что катеты a, b и гипотенуза c таких треугольников выражаются формулами a=2kmn; b=k(m 2 -n 2); c=k(m 2 +n 2), где k, m и n - натуральные числа, такие, что m>n. Треугольники, со сторонами, длины которых равны 3, 4, 5 называются египетскими треугольниками, т. к. они были известны ещё древним египтянам.
Обратная к теореме Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный (признак прямоугольного треугольника).
ДОКАЗАТЕЛЬСТВО.
Пусть в треугольнике ABC AB 2 = AC 2 + BC 2 . Докажем, что угол C - прямой. Рассмотрим прямоугольный треугольник A 1 B 1 C 1 с прямым углом C 1 , у которого A 1 C 1 = AC и B 1 C 1 = BC. По теореме Пифагора A 1 B 1 2 =A 1 C 1 2 +B 1 C 1 2 , и значит, A 1 B 1 2 = AC 2 +BC 2 . Но AC 2 + BC 2 = AB 2 по условию теоремы. Следовательно, A 1 B 1 2 = AB 2 , откуда A 1 B 1 = AB. Треугольники ABC и A 1 B 1 C 1 равны по трём сторонам, поэтому < C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.
Что и требовалось доказать.
Прямоугольные треугольники наравне с равнобедренными и равносторонними занимает свое место среди треугольников, обладая особым набором специфичных свойств, характерных только для этого вида треугольников. Рассмотрим несколько теорем о равенстве прямоугольных треугольников, которые существенно упростят решение некоторых задач.
Первый признак равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников проистекают из трех признаков равенства треугольников, но прямой угол искажает их, расширяет при этом делая проще. Любой из признаков равенства прямоугольных треугольников можно заменить одним из трех основных, но это будет занимать слишком много времени, поэтому были выделены 5 свойств и признаков равенства прямоугольных треугольников.
Очень часто вместо использования основных признаков равенства треугольников, используется метод наложения, когда две фигуры мысленно накладываются одна на другую. Нельзя сказать, что это верно или неверно. Просто еще один способ доказательства, который стоит учитывать. Но нельзя думать, что любой признак можно доказать обычным наложением. Именно поэтому рассмотрим доказательство признаков равенства прямоугольных треугольников через три основных признака равенства треугольников.
Первый признак равенства прямоугольных треугольников гласит: два прямоугольных треугольника равны, если два катета одного треугольника равны двум катетам другого треугольника. Коротко этот признак называют равенством по двум катетам.

Рис. 1. Равенство по двум катетам
Доказать этот признак очень просто. Дано: два катета прямоугольных треугольника равны. Между катетами находится прямой угол, который равен 90 градусам, а значит и угол у треугольников совпадает. Следовательно, два треугольника равны по двум сторонам и углу между ними.
Второй признак
Второй признак читается так: два прямоугольных треугольника равны, если катет и прилежащий острый угол одного треугольника равны катету и прилежащему углу другого треугольника.
Второй признак доказывается исходя из того же утверждения о равенстве прямых углов между собой. Если у треугольников катеты равны, острые углы при них равны, а прямые углы равны по определению, то такие треугольники равны по второму признаку равенства (стороне и двум, прилежащим к ней углам).
Третий признак
Два прямоугольных треугольника равны, если равен катет и противолежащий острый угол.

Рис. 2. Рисунок к доказательству
Сумма острых углов в треугольнике равна 90 градусов. Обозначим углы малыми латинскими буквами для простоты доказательства. Один угол прямой, а два других обозначим буквами a и b в первом треугольнике; c и d во втором треугольнике.
Углы a и d равны между собой по условию задачи.
Вычтем из обеих сторон выражения угол a
То есть, если в двух прямоугольных треугольника два острых углы равны между собой, то и два других острых угла, также будут равны, и мы можем воспользоваться вторым признаком.
Во втором и третьем признаке нужно особенно акцентировать внимание на остром угле, так как прямые углы всегда равны между собой.
Четвертый признак
Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Как было сказано в предыдущем признаке: если острый угол прямоугольного треугольника равен соответствующему острому углу другого прямоугольного треугольника, то и другая пара острых углов треугольников будет равна между собой.
Значит, по условиям этого признака мы имеем равенство гипотенузы и двух острых углов треугольников, а значит такие треугольники будут равны по стороне и двум прилежащим к ней углам (2 признак равенства треугольников)
Пятый признак
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.
Если гипотенуза и катет у двух треугольников соответственно равны, то и вторые катеты таких треугольников буду равны между собой. Это проистекает из теоремы Пифагора.

Рис. 3. Равенство по катету и гипотенузе
Квадрат гипотенузы равен сумме квадратов катетов. Гипотенузы равны между собой, катет одного треугольника равен квадрату другого треугольника, значит, чтобы сумма оставалась верной, и два других катета будут равны между собой.
Что мы узнали?
Мы рассмотрели доказательство пяти признаков равенства треугольников через основные признаки равенства треугольников. Разобрались, почему такое доказательство предпочтительнее наложения и определили путь доказательства, который позволит в любой момент восстановить основные понятия темы в памяти, без излишнего заучивания.
Тест по теме
Оценка статьи
Средняя оценка: 4.6 . Всего получено оценок: 100.
Вспомним из материала предыдущего урока, прямоугольный треугольником называется треугольник, если у него хотя бы один из углов прямой (т. е. равен 90 о).
Рассмотрим первый признак равенства треугольников: если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
Проиллюстрируем данный случай:
Рис. 1. Равные прямоугольные треугольники
Доказательство :
Вспомним о первом равенстве произвольных треугольников.

Рис. 2
Если две стороны и угол между ними одного треугольника и соответствующие им две стороны и угол между ними второго треугольника равны, то данные треугольники равны. Об этом гласит первый признак равенства треугольников, то есть:

Аналогичное доказательство следует и для прямоугольных треугольников:
 .
.
Треугольники равны по первому признаку.
Рассмотрим второй признак равенства прямоугольных треугольников. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 3
Доказательство :

Рис. 4
Воспользуемся вторым признаком равенства треугольников:

Аналогичное доказательство и для прямоугольных треугольников:

Треугольники равны по второму признаку.
Рассмотрим третий признак равенства прямоугольных треугольников: если гипотенуза и прилежащий к ней угол одного прямоугольного треугольника соответственно равны гипотенузе и прилежащему углу другого треугольника, то такие треугольники равны.
Доказательство :

Рис. 5
Вспомним второй признак равенства треугольников:

Рис. 6
Данные треугольники равны, если:

Поскольку известно, что одна пара острых углов у прямоугольных треугольников равна (∠А = ∠А 1), то равенство другой пары углов (∠B = ∠B 1) доказывается следующим образом:
Поскольку АВ = А 1 В 1 (по условию), ∠В = ∠В 1 , ∠А = ∠А 1 . Поэтому треугольники АВС и А 1 В 1 С 1 равны по второму признаку.
Рассмотрим следующий признак равенства треугольников:
Если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, такие прямоугольные треугольники равны.

Рис. 7
Доказательство :
Совместим наложением треугольники АВС и А 1 В 1 С 1 . Предположим, что вершины А и А 1 , а также С и С 1 совместились наложением, а вершина В и точка В 1 не совпадают. Именно этот случай указан на следующем рисунке:

Рис. 8
В данном случае мы можем заметить равнобедренный треугольник АВВ 1 (по определению - по условию АВ = АВ 1). Поэтому по свойству, ∠АВ 1 В = ∠АВВ 1 . Рассмотрим определение внешнего угла. Внешним углом треугольника называется угол, смежный любому углу треугольника. Его градусная мера равна сумме двух углов треугольника, несмежных с ним. На рисунке указано данное соотношение:

Рис. 9
Угол 5 является внешним углом треугольника и равен ∠5 = ∠1 + ∠2. Отсюда следует, что внешний угол больше каждого из углов, несмежных с ним.
Таким образом, ∠АВВ 1 является внешним углом для треугольника АВС и равен сумме ∠АВВ 1 = ∠САВ + ∠АСВ = ∠АВС = ∠САВ + 90 о. Таким образом, ∠АВ 1 В (что является острым углом в прямоугольном треугольнике АВВ 1) не может быть равен углу ∠АВВ 1 , ведь данный угол - тупой по доказанному.
Значит наше предположение касательно расположения точек В и В 1 оказалось неверным, следовательно данные точки совпадают. А значит треугольники АВС и А 1 В 1 С 1 совместились наложением. Поэтому они равны (по определению).
Таким образом, данные признаки вводятся не зря, ведь их можно использовать при решении некоторых задач.
- Омский государственный университет ().
- Справочный портал calc.ru ().
- Учительский портал ().
1. № 38. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В., под редакцией Садовничего В. А. Геометрия 7. М.: Просвещение. 2010 г.
2. Исходя из данных, указанных на рисунке, укажите равные треугольники, если они есть.

3. Исходя из данных, указанных на рисунке, укажите равные треугольники, если они есть. Учитывайте, что АС = АF.

4. В прямоугольном треугольнике к гипотенузе проведены медиана и высота. Угол между ними равен 20 о. Определите величину каждого из острых углов данного прямоугольного треугольника.
Разделы: Математика
Тема: “Признаки равенства прямоугольных треугольников”
Цель: закрепление знаний (свойства прямоугольных треугольников), знакомство с некоторыми признаками равенства прямоугольных треугольников.
Ход урока:
I. Оргмомент.II. Устно.
1. Ответить на вопросы:
- Назвать элементы прямоугольного треугольника.
- Какими свойствами обладают элементы прямоугольного треугольника?
- Докажите, что катет прямоугольного треугольника, лежащий против угла в 30 0 , равен половине гипотенузы.
- Докажите, что если катет прямоугольного треугольника равен половине гипотенузы, то угол лежащий против этого катета равен 30 0 .
- Найти x. Ответ выбрать из треугольника. Буквы какого-то слова находятся в секторах треугольника. Обсуждение в парах (3 мин).
Рисунок 1.
Составили слово “признак”.
III. Изучение нового материалаИзучая треугольники, мы говорим, что он обладает некоторыми свойствами и признаками. А какие признаки равенства треугольников вам известны? Мы сформулировали и доказали свойства прямоугольных треугольников, а сегодня рассмотрим признаки равенства прямоугольных треугольников, будем решать задачи с их применением.
Доказывая равенство треугольников, сколько пар соответственно равных элементов отыскивали? А возможно ли доказать равенство прямоугольных треугольников по двум катетам?
Перед вами два прямоугольных треугольника АВС и А 1 В 1 С 1 , у них соответственно равны катеты. Докажите, если это возможно, их равенство.
№1. (По двум катетам)

Рисунок 2.
Дано: АВС и А 1 В 1 С 1 , В=В 1 =90 0 , АВ = А 1 В 1 , ВС = В 1 С 1
Доказать: АВС = А 1 В 1 С 1
Как прозвучит признак? (Затем задача №1)
№2. (По катету и прилежащему к нему острому углу)

Рисунок 3.
Дано: АВС и А 1 В 1 С 1 , В=В 1 =90 0 , ВС = В 1 С 1, С= С 1
Доказать: АВС = А 1 В 1 С 1
Как прозвучит признак? (Затем задача №2)
№3. (По гипотенузе и острому углу)

Рисунок 4.
Дано: АВС и А 1 В 1 С 1 , В=В 1 =90 0 , АС = А 1 С 1, А= А 1
Доказать: АВС = А 1 В 1 С 1
Как прозвучит признак? (Затем задача №3)
Задачи. Найти равные треугольники и доказать их равенство.

Рисунок 5.
IV. Закрепление изученного на уроке.Решить следующую задачу.

Рисунок 6.
Дано: АВС, А 1 В 1 С 1 , DAB=CBA=90 0 , АD = BD
Доказать: CAB=DBA.
Обсуждение в четверках (3 мин).
Зачем задача из учебника №261 с записью.

Рисунок 7.
Дано: АВС – равнобедренный, AD и CE – высота АВС
Доказать: AD = CE
Доказательство:
V. Задание на дом.
П.35 (три признака), №261 (доказать, что АОС - равнобедренный), №268 (признак равенства прямоугольных треугольников по катету и противолежащему углу).
На следующем уроке геометрии мы продолжим знакомство с признаками равенства прямоугольных треугольников. Отметки выставлю также в следующий раз по результатам за 2 урока.
Дополнительно. Найти равные треугольники.