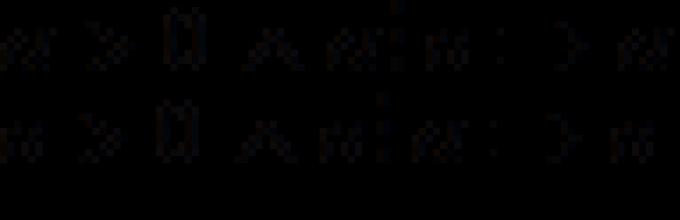Знаци на деливост. Деливост на збир, разлика, производ. Својства на деливост на природните броеви Конзистентен систем на аксиоми се нарекува независен ако ниту една од аксиомите на овој систем не е последица на другите аксиоми на овој систем

Нека се дадени природни броевиаИб. Велат дека бројкатааделив со бројб, ако има таков природен бројq, Штоа = bq.

Во овој случај бројот бповикани делител на број А, и бројот А - множители на бројот б.

На пример, 24 се дели со 8, бидејќи постои такво нешто q= 3, што е 24 = 8*3. Можеме да кажеме поинаку: 8 е делител на бројот 24, а 24 е множител на бројот 8.

Во случај Аподелено со б, напишете:. Овој запис често се чита вака: „ Аповеќекратни б».

Забележете дека концептот „деленик на даден број“ треба да се разликува од концептот „делител“, кој го означува бројот со кој се дели. На пример, ако 18 се подели со 5, тогаш бројот 5 е делител, но 5 не е делител на бројот 18. Ако 18 се подели со 6, тогаш во случајот на концептот „деленик“ и „деленик на даден број“ исто.

Од дефиницијата на односот на деливост и еднаквост А = 1*А, важи за секој природен број a, следува дека 1 е делител кој било природен број.

Ајде да откриеме колку делители може да има природен број. Ајде прво да ја разгледаме следната теорема.

Теорема.Разделник бдаден број Ане ја надминува оваа бројка. Ако, тогаш.

Доказ.Од, тогаш постои такво што a = bq, значи, а-б = bq - b = b*(q- 1). Затоа што тогаш. Тогаш и затоа.

Од оваа теорема произлегува дека множеството делители на даден број е конечно. Да ги повикаме, на пример, сите делители на бројот 36. Тие формираат конечно множество (1, 2, 3, 4, 6, 9, 12, 18, 36).

Својства на деливост

Знаеме дека односот на деливост на множество Нима голем број на својства, особено, тој е рефлексен, антисиметричен и транзитивен. Сега, имајќи ја дефиницијата на односот на деливост, можеме да ги докажеме овие и други својства на истата.

Теорема.Релацијата на деливост е рефлексна, т.е. секој природен број е делив само по себе.

Доказ.За секое природно Аеднаквоста е вистина . Бидејќи 1 e N, тогаш, по дефиниција на односот на деливост, .

Теорема.Релацијата на деливост е антисиметрична, т.е. Ако и тогаш.

Доказ. Да го претпоставиме спротивното, т.е. Но, тогаш да , според теоремата дискутирана погоре.

По услов И . Потоа, според истата теорема,.

Нееднаквостите ќе бидат фер само кога , што е во спротивност со условите на теоремата. Следствено, нашата претпоставка е неточна и теоремата е докажана.

Теорема.Релацијата на деливост е преодна, т.е. Ако И , Тоа .

Доказ.Бидејќи , q,Што А= bq,и бидејќи , тогаш постои таков природен број стр, Што . Но, тогаш имаме: . Број pq-природен. Тоа значи, по дефиниција на односот на деливост,.

Теорема(знак за деливост на збирот). Ако секој од природните броеви а1, а2..., нагоределив со природен број б, потоа нивниот збир a1 + a2 +... + нагоресе дели со овој број.

Доказ. Бидејќи , тогаш постои природен број таков што . Бидејќи , тогаш постои таков природен број , Што . Продолжувајќи со расудувањето, добиваме дека ако , тогаш постои таков природен број , Што . Овие еднаквости ни овозможуваат да го трансформираме збирот a1 + a2 +... + нагорево износ од типот bq1+ bq2+ ... + bqn.Да го извадиме заедничкиот фактор од загради б,и добиениот природен број во загради q1 + q2 +... + qnозначено со буквата q. Потоа а1+ а2+ ... + нагоре= b(q1+ q2+ ... + qn) = bq, т.е. сума а1+ а2+ ... + нагореиспадна дека е претставен како производ на бројот би некој природен број q.Тоа значи дека износот а1+ а2+ ... + нагореподелено со б, Q.E.D.

На пример, без да правиме пресметки, можеме да кажеме дека збирот 175 + 360 + 915 е делив со 5, бидејќи секој член од оваа сума е делив со 5.

Теорема(тест на деливост на разликата). Доколку бројките а1И а2се поделени на би , тогаш нивната разлика се дели со б.

Доказот за оваа теорема е сличен на доказот за тестот за деливост за збир.

Теорема(знак за деливост на дело). Доколку бројот Ае поделена на б,потоа производ на формата О,Каде xÎ N, делив со б.

Доказ. Бидејќи , тогаш постои таков природен број q,Што . Ајде да ги помножиме двете страни на оваа еднаквост со природен број X.Потоа О= (bq) x,од каде, врз основа на асоцијативното својство на множење (bq)x = b(qx)и затоа, О= b (qx),Каде qx-природен број. Според дефиницијата на односот на деливост, , Q.E.D.

Од докажаната теорема произлегува дека ако еден од множителите на производот е делив со природен бројb, тогаш целиот производ е делив со b.

На пример, производот 24

Дефиниција.Нека се дадени природните броеви a и b. За бројот a се вели дека е делив со број b ако има природен број q таков што a = bq.

Во овој случај бројот б повикани делител на а , и бројот a е множител на b.

На пример, 24 е делив со 8, бидејќи такво нешто постои q = 3, што е 24 = 8×3. Можеме да кажеме поинаку: 8 е делител на бројот 24, а 24 е множител на бројот 8.

Во случај кога Аподелено со б,напишете: a M b. Овој запис често се чита вака: „многукратно б“.

Забележете дека концептот „деленик на даден број“ треба да се разликува од концептот „делител“, кој го означува бројот со кој се дели. На пример, ако 18 се подели со 5, тогаш бројот 5 е делител, но 5 не е делител на бројот 18. Ако 18 се подели со 6, тогаш во овој случај концептите на „делител“ и „делител на даден број“ се совпаѓаат.

Од дефиницијата на односот на деливост и еднаквоста a = 1 × А,валидни за секој природен А,следува дека 1 е делител на кој било природен број.

Ајде да откриеме колку делители може да има природен број А.Ајде прво да ја разгледаме следната теорема.

Теорема 1. Делителот b на даден број a не го надминува овој број, т.е. ако a M b, тогаш b £ a.

Доказ.Бидејќи a M b, тогаш постои qО N такво што a = bq и, според тоа, a - b = bq - b = b ×(q - 1). Бидејќи qО N, тогаш q ³ 1. . Тогаш b ×(q - 1) ³ 0 и, според тоа, b £ a.

Од оваа теорема произлегува дека множеството делители на даден број е конечно. Да ги повикаме, на пример, сите делители на бројот 36. Тие формираат конечно множество (1,2,3,4,6,9, 12, 18,36).

Во зависност од бројот на делители, природните броеви се делат на прости и композитни броеви.

Дефиниција.Прост број е природен број поголем од 1 кој има само два делители - еден и самиот број.

На пример, 13 е прост бидејќи има само два делители: 1 и 13.

Дефиниција.Композитен број е природен број кој има повеќе од два делители.

Значи, бројот 4 е составен, има три делители: 1, 2 и 4. Бројот 1 не е ниту прост ниту композитен број поради тоа што има само еден делител.

Броевите кои се множители на даден број може да се именуваат колку што сакате, има бесконечен број од нив. Така, броевите кои се множители на 4 формираат бесконечна серија: 4, 8, 12, 16, 20, 24, .... и сите тие може да се добијат со формулата a = 4q,Каде qзема вредности 1, 2, 3,... .

Знаеме дека односот на деливост на множеството N има голем број својства, особено, таа е рефлексна, антисиметрична и преодна. Сега, имајќи ја дефиницијата на односот на деливост, можеме да ги докажеме овие и други својства на истата.

Теорема 2. Релацијата на деливост е рефлексивна, т.е. Секој природен број е делив само по себе.

Доказ.За секое природно Аеднаквоста е вистина a = a× 1. Бидејќи 1 О N тогаш, по дефиниција на релацијата на деливост, aMa.

Теорема 3. Релацијата на деливост е антисиметрична, т.е. ако a M b и a ¹ b, тогаш .

Доказ.Да го претпоставиме спротивното, т.е. дека bMa. Но, тогаш a £ b, според теоремата дискутирана погоре.

По услов a M b и a ¹ b. Потоа, според истата теорема, b £ a.

Неравенките a £ b и b £ a ќе важат само кога a = b, што е во спротивност со условите на теоремата. Затоа, нашата претпоставка е неточна и теоремата е докажана.

Теорема 4. Релацијата на деливост е преодна, т.е. ако а M b и b M c, потоа a M c.

Доказ.Бидејќи a M b, q,Што А = bq,и бидејќи bM s,тогаш постои таков природен број р, Што б = срНо, тогаш имаме: А = b q = (просечно) q = c(pq).Број pq -природен. Ова значи, по дефиниција на односот на деливост, А. М с.

Теорема 5(знак за деливост на збирот). Ако секој од природните броеви a 1, a 2,...a n е делив со природен број b, тогаш нивниот збир a 1 + a 2 +... + a n е делив со овој број.

На пример, без да правиме пресметки, можеме да кажеме дека збирот 175 + 360 +915 е делив со 5, бидејќи секој член од оваа сума е делив со 5.

Теорема 6(тест на деливост на разликата). Ако броевите a 1 и a 2 се делат со b и a 1 ³ a 2, тогаш нивната разлика a 1 - a 2 се дели со b.

Теорема 7(знак за деливост на дело). Ако бројот a е делив со b, тогаш производот е од формата ax, каде што x e N. се дели со b.

Од теоремата произлегува дека Ако еден од множителите на производот е делив со природен број b, тогаш целиот производ е делив со b.

На пример, производот 24 × 976 × 305 е делив со 12, бидејќи факторот 24 е делив со 12.

Да разгледаме уште три теореми поврзани со деливоста на збир и производ, кои често се користат при решавање на проблеми со деливост.

Теорема 8. Ако во збирот еден член не се дели со бројот b, а сите други членови се деливи со бројот b, тогаш целиот збир не се дели со бројот b.

На пример,збирот 34 + 125 + 376 + 1024 не се дели со 2, бидејќи 34: 2.376: 2.124: 2, но 125 не се дели со 2.

Теорема 9. Ако во производот ab факторот a се дели со природниот број m, а факторот b се дели со природниот број n, тогаш a b се дели со mn.

Валидноста на оваа изјава произлегува од теоремата за деливост на производ.

Теорема 10. Ако производот ac е делив со производот bc, а c е природен број, тогаш a се дели и со b.

Дефиниција.Тие го велат тоа бројот a се дели со бројот b,доколку постои таков број вÎ Н 0 , Што А=В· Со.

Во случај кога Аподелено со Внапиши: а в.Тие читаат: „ Аподелено со В» ; « Аповеќекратни В»; « В- делител А» . На пример, 12 се дели со 6, бидејќи постои такво нешто Со= 2, тоа 12 = 6 2, инаку 12 6.

Коментар. Евиденција и А :Вне се еквивалентни. Првиот значи дека помеѓу бројките АИ Впостои релација за деливост (евентуално цел број Аподели со број В). Второ, постои ознака за количници АИ В.

Релацијата за деливост има голем број својства.

1°. Нулата е делива со кој било природен број, т.е.

(" ВÎ Н ) .

Доказ. 0 = В· 0 за секого V,од тука по дефиниција следува дека 0 В.

2°. Ниту еден природен број не е делив со нула, т.е. (" АÎ Н ) [А 0].

Доказ (со контрадикторност). Нека постои вÎ Н 0 , такви што А= 0· Со,но според условот А≠ 0, што значи без разлика Сооваа еднаквост не важи. Тоа значи дека нашата претпоставка за постоењето Соне беше во право и А 0.

3°. Секој ненегативен цел број е делив со еден, т.е.

("АÎ Н ) [А 1].

Доказ. А= 1· А=>А 1.

4°. Секој природен број е делив само по себе (рефлексивност), т.е. АÎ Н ) [а а].

Доказ. А= А· 1 Þ а а.

5°. Разделник Вдаден природен број Ане ја надминува оваа бројка, т.е. ( и воÙ А> 0) Þ ( А≥ В).

Доказ. Бидејќи и во,Тоа А= В · Со,Каде вÎ Н 0 . Ајде да го одредиме знакот на разликата А– В.

А–В= Сонцето– В= В(Со– 1), бидејќи А> 0, Тоа Со≥ 1, затоа В(Со– 1) ≥ 0, што значи А–В≥ 0 Þ А≥В.

6°. Релацијата на деливост е антисиметрична, т.е.

("а, воÎ Н 0 )[(а воÙ во а) Þ А=В].

Доказ.

1 случај . Нека А> 0,В> 0, тогаш имаме:

(по својство 5°). Средства, А = В.

Случај 2. Нека барем еден од броевите Аили Ве еднакво на 0.

Нека А= 0, тогаш В= 0 до 2°, бидејќи во спротивно Вне можеше да се подели на А.Средства А=В.

7°. Релацијата на деливост е преодна, т.е.

(„а, во, соÎ Н 0 ) [(а воÙ во со)Þ и со].

Доказ. и воÞ ($ На)[А=VK];во соÞ ($ ℓ )[В= cℓ].

А = VK= (sℓ)На= Со(ℓк), ℓк -производ на два ненегативни цели броеви ℓ И Наи затоа самиот е ненегативен цел број, т.е. а.с.

8°. Ако секој од броевите АИ Вподелено со Со,тогаш нивниот збир А+ Вподелено со Со,тие. (" а, б, вÎ Н 0 ) [(а соÙ во со) Þ ( А+В) Со].

Доказ, и соÞ А= ск, во сÞ В= cℓ.

А+В= ск+cℓ=Со(k + ℓ), бидејќи На+ ℓ е ненегативен цел број, што значи ( a + b) Со.

Докажаната изјава е вистинита и во случај кога бројот на поими е повеќе од два.

Ако секој од броевите А 1 , ...,а стрподелено со Со,тогаш нивниот збир А 1 + ... + а стрподелено со Со.

Згора на тоа, ако бројките АИ Все поделени на Со,и А≥ В, тогаш нивната разлика А–Вподелено со Со.

9°. Доколку бројот Аподелено со Со, потоа производ на формата О,Каде xÎ Н 0 , поделено со Со,тие. и соÞ ( " x О Н 0 )[секира со].

Доказ. и соÞ А=ск,но тогаш О= skkh = Со(На· X), к, хÎ Н 0 , Средства ах с.

Последица од 8°, 9°.

Ако секој од броевите А 1 ,А 2 , ...,а стрподелено со Со,тогаш какви и да се бројките X 1 ,X 2 , ... , x nброј А 1 X 1 + а 2 X 2 + ... + a n x nподелено со Со.

10°. Ако акподелено со сонце,и Со≠ 0, Тоа Аподелено со V,тие. ( како сонцеÙ Со≠ 0) Þ а в.

Доказ.

ак= Сонцето· До; ак= (VK) · СоÙ Со≠ 0 Þ А=VK=> и во.

Знаци на деливост

Има проблеми во кои, без делење, треба да одредите дали природниот број е делив или не Адо природен број В.Најчесто ваквите проблеми се јавуваат кога бројот Амора да се факторизира. При вакви проблеми се користат критериуми за деливост. Тест за деливост е реченица која ви овозможува да одговорите на прашањето дали одреден број е делив со даден делител или не, без да се изврши самото делење.

При примена на критериумот за деливост, сепак треба да се делите, се разбира. Тестот за деливост на број со 3 е добро познат од училиште Дали бројот 531246897 се дели со 3? За да одговориме на прашањето, го одредуваме збирот на цифрите на овој број 5 + 3 + 1 + 2 + 4 + 6 + 8 + 9 + 7 = 45, бидејќи 45 се дели со 3, а потоа дадениот број се дели со 3.

Значи, прашањето за деливост на даден природен број се сведува на прашањето за деливост на помал природен број.

Критериумите за деливост зависат од системот на броеви. Да разгледаме некои знаци на деливост во декадниот броен систем.

ПОДЕЛБА НА БРОЕВИ. ЗНАЦИ НА ПОДЕЛБА

Да ја разгледаме врската на деливост во прстенот на цели броеви. Велат дека бројката аподелено со б, постои таков цел број q, за што a = qb.
Следниве својства важат за односот на деливост.
Имотот 1.Ако аподелено со бИ бподелено со в, Тоа аподелено со в.
Имотот 2.Ако а 1, … , аnсе поделени на б, тогаш а 1+ … + аnподелено со б.

Имотот 3.Ако а 1 се дели со б 1, … , аnподелено со бn, тогаш а 1…аnподелено со б 1…бn.
Важи следнава теорема за делење со остаток.
Теорема.За произволни цели броеви аи природен број бима само еден број qИ ртакви што a = qb + rи 0 р< b . Број qсе нарекува нецелосен количник, а бројот р– остатокот.
Ви претставуваме два доказа за оваа теорема. Првиот од книгата.
Доказ 1.Прво нека а 0. Броевите ќе ги запишуваме еден по друг а, а – б, а - 2б, ...додека не се појави негативен број. Нека последниот од ненегативните членови на оваа низа е бројот a–qb.Осврнувајќи се на тоа како r,имаме a = qb + r.Очигледно е дека р< b (инаку бројот r – b = a –(q + 1)бби било ненегативно).
Нека сега а< 0. Расудувајќи слично како претходното, ќе ја запишеме низата броеви a, a + b, a + 2б, ...додека не се појави првиот ненегативен број р(лесно е да се провери тоа р< b ). Нека р = а + q" б. Потоа, означувајќи - q"преку q, добиваме a = qb + r. Q.E.D.
Да ја докажеме уникатноста, т.е. дека од a = qb + rИ a = q"b + r"треба да q = q"И r = r". Во овој случај имаме еднаквост qb + r = q"b + r", каде r – r" =(q" – q)б,т.е. r-r"поделено со б. Но | r-r"| < б, и еднаквост r – r" =(q" – q)бможно само ако r – r" = 0. Но тогаш ( q" – q)б= 0 и затоа q" – q = 0.
Да дадеме уште еден доказ со геометриска интерпретација.
Доказ 2.Забележете дека системот на интервали [ qb, (q + 1)б), Каде q– цел број, го опфаќа целото множество цели броеви. Број аспаѓа во еден и само еден од овие интервали, односно има само еден q, за што qbа< qb + b. Да означиме r = a – qb.Тогаш ќе имаме: a = qb + rи 0 р< b .
Поделбата со теорема за остаток може да се користи за да се најде најголемиот заеднички делител gcd( а, б) два природни броја аИ б.

Потсетиме дека најголемиот заеднички делител на два природни броја е аИ бсе нарекува најголем од броевите кои се делители аИ бистовремено. Да докажеме дека постои таков број. Навистина, ако ве делител на природен број а, потоа | в| а. Според тоа, секој природен број има конечен број делители. Така, бројот на заеднички делители на два природни броја е конечен и, според тоа, меѓу нив има најголем елемент - најголемиот заеднички делител.

Забележете дека од еднаквоста а = qb + р, каде што 0 р < б, следува дека секој делител на броеви аИ бе делител на броеви бИ ри обратно. Затоа, GCD( а, б) = GCD ( б, р). Ако рсе разликува од нула, тогаш делиме бна рсо остатокот. Добиваме б = q 1р + р 1, каде што 0 р 1 < ри GCD( б, р) = GCD ( р, р 1). Продолжувајќи го овој процес на поделба, доаѓаме до ситуација кога рк+1 = 0, т.е. рк– 1 се дели со рки, според тоа, GCD ( а, б) = GCD ( б, р) = GCD ( р, р 1) = … = gcd ( рк-1, рк) = рк.
Овој метод за наоѓање на најголемиот заеднички делител е содржан во Евклидовите елементи и се нарекува Евклидовиот алгоритам.
Пример.Најдете го најголемиот заеднички делител на броевите 168 и 70.
Имаме, 168 = 270 + 28, 70 = 228 + 14, 28 = 214. Така, GCD(168, 70) = 14.
Броеви аИ бсе нарекуваат еквирезид (кога се делат со в), ако нивните остатоци се еднакви.
Следниве својства се валидни за релацијата equiresidue.

Имотот 1. а И беквистатски (кога се дели со в) ако и само ако а – бподелено со в.

Доказот е очигледен.
Имотот 2.Ако а 1, … , аn б 1, … , бn, Тоа а 1 + … + аnИ б 1+ … + бnисто така остануваат.

Доказот е очигледен.
Имотот 3.Ако а 1, … , аnсоодветно еквистатски в б 1, … , бn, Тоа а 1... аnИ б 1…бnисто така остануваат.

Доказот го спроведуваме со индукција на n. За n=1 изјава е очигледна. Да ја покажеме неговата валидност за два фактори, т.е n=2. имаме а 1а 2 – б 1б 2 = (а 1 – б 1)а 2 + б 1(а 2 – б 2). Затоа, ако а 1 – б 1 се дели со вИ а 2 – б 2 се дели со в, тогаш а 1а 2 – б 1б 2 се дели со в. Да претпоставиме дека изјавата е точна за n– 1 и докажете дека е точно за n. Да ги претставиме делата а 1... аnИ б 1…бnво форма а 1... аn = (а 1... аn-1)анИ б 1…бn = (б 1…бn-1)бн. Според хипотезата за индукција, а 1... аn-1 и б 1…бn-1 се еквистатични. Применувајќи ја докажаната изјава за два фактора, добиваме дека броевите ( а 1... аn-1)анИ ( б 1…бn-1)бнеквирезидуален.
Последица.Ако аИ бсе еквистатични, тогаш аnИ бnеквирезидуален.

Забележете дека еднаквоста на броевите аnИ бnможе да се докаже директно со помош на формулата аn– бn = (а – б)(ан- 1 + ан-2б + … + abn-2 + бн-1).
Ајде да погледнеме примери за решавање проблеми со користење на овие својства.
Пример 1.Дознајте дали бројот 1316 се дели со три
Решение.Бројот 13, кога се дели со 3, е еквивалентен на 1, затоа, 1316 е еднаков на 116 = 1. Бројот 2 е еднаков на –1, затоа 225 со (-1)25 = -1. Бројот 5 е equiremainder со –1, затоа, 515 е equiremainder со (-1)15 = -1. Така, бројот 1316 – 225 515 е еднаков на 1 – (-1)(-1) = 0, т.е. овој број е делив со 3.
Пример 2.Докажете дека бројот 1110 – 1 е делив со 100.
Решение.Имаме 1110 – 1 = 10 (119 + 118+ … + 1). Бројот 11, кога се дели со 10, е еквистатски со 1. Според тоа, збирот на броевите во заградата од десната страна е еднаков со 1 + 1 + ... + 1 = 10 и затоа е делив со 10 Така, оригиналниот број е делив со 100.
Пример 3.Докажете го тоа за секое природно nброј n 3 + 11nделив со 6.
Решение. 11nкога се дели со 6 е еднаков на остаток со – n. Според тоа, оваа бројка е еднаква на n 3– n = n(n - 1) (n+ 1). На десната страна е производ на три последователни природни броеви (или 0). Еден од нив мора да биде парен, а другиот е делив со 3. Така, целиот производ е делив со 6.
Пример 4.Докажете дека бројот + е делив со 7.
Решение. 2222 и –4 се еквистатични кога се делат со 7, 5555 и 4 се исто така еквистатични. Според тоа, + е еднакво на -45555 + 42222 = -42222(43333 – 1) = -42222(641111 – 1) = (641110+…+1). Бидејќи 63 е делив со 7, тогаш овој број се дели со 7.
Пример 5.Најдете го остатокот кога делите број со 7.
Решение.Забележете дека 1000 кога се дели со 7 е еднакво на –1. Затоа еквивалентно со –10. Последователните поими се исто така еквиреостаток со –10 и, според тоа, целиот збир е еквиреаиндер со бројот –100, кој пак, е еквиреаиндер со 5. Така, бараниот остаток е 5.

Пример 6.Дали 2006 година може да се претстави како разлика на квадратите на два природни броја?

Одговори.бр. Ако само 2006 = а 2 – б 2 = (а – б)(а + б), потоа или а – били а + бби бил парен број. Но, тогаш другиот број би бил парен, што значи а 2 – б 2 би бил делив со 4. Но, 2006 година не се дели со 4.

Сега да разгледаме некои знаци на деливост.
1. Тест за деливост со 2.
Бројот се дели со 2 ако бројот формиран од неговата последна децимална цифра е делив со 2.
2. Тест за деливост со 4.
Бројот се дели со 4 ако бројот формиран од последните две цифри во неговата децимална нотација е делив со 4.
Доказот произлегува од фактот дека бројот 100 и неговите множители се деливи со 4.
3. Тест за деливост со 5.
Бројот се дели со 5 ако неговата последна децимална цифра е 0 или 5.
4. Тест за деливост со 3.
Бројот се дели со 3 ако збирот на броевите формирани од неговите цифри во децимална нотација е делив со 3.
Доказ.Бројот 10 е еднаков на 1. Затоа, 100 е еднаков на 1, 1000 е еднаков на 1, итн. Така, бројот аn…а 1а 0=а 0+ а 110+…+аn 10nеквистатски со а 0+а 1+ … +аn.

Забележете дека докажавме малку повеќе отколку што беше потребно, имено, докажавме дека бројот го дава, кога се дели со три, истиот остаток како збирот на броевите формирани од цифрите на овој број во децимална нотација.

5. Тест за деливост со 9.
Бројот се дели со 9 ако збирот на броевите формирани од неговите цифри во децимална нотација е делив со 9.
Доказот е сличен на претходниот.
6. Тест за деливост со 8.
Бројот се дели со 8 ако бројот формиран од последните три цифри во децималната нотација е делив со 8.
Доказот произлегува од фактот дека бројот 1000 и неговите множители се деливи со 8.
7. Тест за деливост со 11.
Бројот се дели со 11 ако алгебарскиот збир на броевите формирани од неговите цифри во наизменична децимална нотација е делив со 11.
Доказ.Бројот 10 е еднаков на –1. Според тоа, 100 е резервен остаток со (-1)(-1) = 1, 1000 е резервен остаток со -1 итн. Така, бројот аn…а 1а 0=а 0+ а 110+…+аn 10nеквистатски со а 0-а 1 + … + (-1)nаn.
Како пример, земете го бројот 3516282. Алгебарскиот збир на неговите цифри е 2 – 8 + 2 – 6 + 1 – 5 + 3 = -11. Така, овој број се дели со 11.
8. Комбиниран знак на деливост со 7, 11 и 13.
Бројот се дели со 7, 11 или 13 ако алгебарскиот збир на броевите формирани од тројките од цифрите на дадениот број во наизменична децимална нотација е делив со 7, 11 или 13 соодветно.
Доказ.Забележете дека производот на броевите 7, 11 и 13 е еднаков на 1001. Според тоа, бројот 1000 кога се дели со 7, 11 или 13 е еднаков на –1. Следно, продолжуваме како во тестот за деливост со 11.
Како пример, земете го бројот Бројот 295 – 623 + 42 = -286 е делив со 11 и 13, но не се дели со 7. Затоа, овој број е делив со 11 и 13, но не се дели со 7.
9. Тест за деливост со 37.
Бројот се дели со 37 ако збирот на броевите формирани од тројките од цифрите на дадениот број во децимална нотација е делив со 37 соодветно.
Доказот произлегува од фактот дека бројот 1000 кога се дели со 37 е еднаков на 1.
Забележете исто така дека трицифрените броеви 111, 222, ..., 999 се деливи со 37.
Лесно е да се види дека броевите се деливи со 37.

Да ги искористиме својствата на деливост за да го решиме следниот проблем, предложен на креативен натпревар за наставници по математика во Москва во 2004 година.
Задача.На таблата има испишан број.... Да ја поделиме неговата децимална нотација произволно на два броја и да ги собереме. Ќе извршиме слична операција со добиените броеви и така додека не добиеме едноцифрен број. Кои едноцифрени броеви може да се добијат на овој начин?
Решение.Децималната ознака на даден број нека се подели на броеви xИ y.Тогаш оригиналниот број има форма x 10...0 + y, а бројот добиен како резултат на наведената операција е еднаков на x+y. Ајде да ја разгледаме разликата помеѓу овие бројки: ( x 10...0 + y) - (x+y) = 9...9x.Бидејќи оваа разлика е делива со 9, првобитните и добиените броеви имаат ист остаток кога се делат со 9. Затоа, секогаш кога ќе се изврши оваа операција, овој остаток не се менува. Директната проверка покажува дека остатокот од делењето со 9 од оригиналниот број е 2. Тоа значи дека како резултат на овие операции може да се добие само бројот 2.

Вежби

1. Со која цифра завршува бројот: а) 99999; б) 3999; в) 71000; г) 3377 + 7733?

2. Докажете дека производот на кои било три последователни природни броеви е делив со 6.

3. Докажете дека производот од кои било пет последователни природни броеви е делив со 120.

4. Најди ги сите природни броеви n > 1, за што n 3 – 3 се дели со n– 1.

5. Докажи дека за секој природен nброј n 3 + 2nделив со 3.

6. Докажи дека за секој природен nброј n 5 + 4nделив со 5.

7. Докажи дека за секој природен nброј n 2 + 1 не се дели со 3.

8. Докажи дека за секој природен nброј n 3 + 2 не се дели со 9.

9. Докажи дека за кој било парен природен број nброј n 3 – 4nделив со 48.

10. Докажи дека за било чудно природно nброј n 6 – n 4 – n 2 + 1 се дели со 128.

11. Докажи дека за сите цели броеви аИ бброј а 2 + 9ab+ б 2 се дели со 11.

12. Докажи дека ако а 2 + 9ab + б 2 се дели со 11, а потоа бројот а 2 – б 2 се дели со 11.

13. Докажи дека ако 56 а = 65б, потоа бројот а + бкомпозитни.

14. Докажи дека ако бројот е 3 n + 2мсе дели со 23, тогаш бројот е 17 n + 19мделив со 23.

15. Докажи дека бројот 31974 + 51974 е делив со 13.

16. Докажи дека бројот 2110 – 1 е делив со 2200.

17. Докажи дека за секој природен nброј n 2 – 3n+ 5 не се дели со 121.

18. Нека С(n) – збирот на цифрите во децималната ознака на бројот n. Најди ги сите природни n, за што важи еднаквоста n + С(n) + С(С(n)) = 1993.

Литература
1. Врапчиња на деливост. – М.: Наука, 1980 година.

2. Математички слободни активности. - М.: Мир, 1972 година.

3. , Фомин математички кругови. – Киров, 1994 г.
4. Проблеми на Олимпијадата Горбачов по математика. – М.: МТСНМО, 2004 година.
5. Кордемски такт. – М.: Наука, 1991 година.
6. Московски математички олимпијади 1993 – 2005. Уреди. – М.: МТСНМО, 2006 година.

7. Покана за теорија на броеви. – М.: Наука, 1980 година.
8. и други Избрани задачи и теореми на елементарната математика. Дел 1, аритметика и алгебра. – М – Л.: Држава. ед. техничко-теорет. литература, 1950 година.

Дефиниција. Нека се дадени природните броеви a и b. За бројот a се вели дека е делив со број b ако има природен број q таков што a = bq.

Во овој случај се повикува бројот b делител на броја, а бројот a е множители на бројотб.

На пример, 24 е делив со 8, бидејќи постои q =3 така што 24 = 8·3. Може да се каже поинаку: 8 е делител на бројот 24, а 24 е множител на бројот 8. Во случај кога a се дели со b, пишуваат: a: . б. Овој запис „“ се чита и вака: „а е множител на b“. Забележете дека концептот „деленик на даден број“ треба да се разликува од концептот „делител“, кој го означува бројот со кој се дели. На пример, ако 18 се подели со 5, тогаш бројот 5 е делител, но 5 не е делител на бројот 18. Ако 18 дели 6, тогаш во овој случај концептите на „делител“ и „делител на дадена број“ се совпаѓаат.

Од дефиницијата на релацијата за деливост и еднаквоста a = 1·a, која важи за секој природен број a, произлегува дека 1 е делител на кој било природен број.

Ајде да откриеме колку делители може да има природниот број a. Ајде прво да ја разгледаме следната теорема.

Теорема 1. Делителот b на даден број a не го надминува овој број, т.е. Ако

О: . б, потоа б< а.

Доказ. Бидејќи а: . b, тогаш постои q Є N така што a = bq u, што значи a-b = bq – b= b (q - 1). Бидејќи q Є N, тогаш q≥ 1. Тогаш b· (q - 1) ≥ 0 и затоа , b ≤ a.

Од оваа теорема произлегува дека множеството делители на даден број е конечно. Да ги повикаме, на пример, сите делители на бројот 36. Тие формираат конечно множество (1,2,3,4,6,9,12,18,36).

Во зависност од бројот на делители, природните броеви се делат на прости и композитни броеви.

Дефиниција. Прост број е природен број кој има само два делители - еден и самиот број.

На пример, бројот 13 е прост бидејќи има само два делители: 1 и 13.

Дефиниција. Композитен број е природен број кој има повеќе од два делители.

Значи, бројот 4 е составен, има три делители: 1,2 и 4.

Бројот 1 не е ниту прост ниту композитен број поради фактот што има само еден делител.

Броевите што се множители на даден број може да се именуваат колку што сакате - има бесконечен број од нив. Така, броевите кои се множители на 4 формираат бесконечна серија: 4, 8, 12, 16, 20, 24, ..., и сите може да се добијат со формулата a = 4q, каде што q ги зема вредностите 1, 2, 3,... .

Знаеме дека релацијата на деливост има голем број својства, особено, таа е рефлексна, антисиметрична и транзитивна. Сега, имајќи ја дефиницијата на односот на деливост, можеме да ги докажеме овие и други својства на истата.

Теорема 2. Релацијата на деливост е рефлексивна, т.е. Секој природен број е делив само по себе.

Доказ. За секој природен број a, еднаквоста a = a·1 е точно. Од 1 Є N, значи, по дефиниција на односот на деливост, a: . А.

Теорема 3. Релацијата на деливост е антисиметрична, т.е. ако а: . b и a ≠ b,

Тоа b ⁞͞ a.

Доказ. Да го претпоставиме спротивното, т.е. тоа б ⁞ а. Но, тогаш a ≤ b, според теоремата дискутирана погоре.

По услов и ⁞ . b и a ≠ b. Потоа, според истата теорема, b ≤ a.

Неравенките a ≤ b и b ≤ a ќе важат само кога a = b, што е во спротивност со условите на теоремата. Затоа, нашата претпоставка е неточна и теоремата е докажана.

Теорема 4. Релацијата на деливост е преодна, т.е. ако а ⁞ б и б ⁞ s, потоа a ⁞ Со.

Доказ. Бидејќи а: . b, тогаш постои природен број q таков што a = bq, и бидејќи b ⁞ c, тогаш постои природен број p таков што b = cf. Но тогаш имаме: a = bq = (cp)q = c(pq) - Бројот pq е природен број. Ова значи, по дефиниција на односот на деливост,

А ⁞ Со.

Теорема 5 (тест за деливост на збирот). Ако секој од природните броеви a 1, a 2, ..., a n е делив со природен број b, тогаш нивниот збир a 1 + a 2 + ... + a n е делив со овој број.

Доказ. Од 1 ⁞ b, тогаш постои природен број q 1 таков што a 1 =bq 1. Од 2 ⁞ b, тогаш постои природен број q 2 таков што a 2 = bq 2 . Продолжувајќи со расудувањето, добиваме дека ако a n: . b, тогаш постои природен број q n таков што a n = bq n. Овие еднаквости ни овозможуваат да го трансформираме збирот a 1 + a 2 + ... + a n во збир од формата bq 1 + bq 2 + ... + bq n. Да го извадиме заедничкиот фактор b од заградите и да го означиме добиениот природен број q 1 + q 2 + ... + q n со буквата q. Потоа а 1+ a 2 + ... + a n = b(q 1 + q 2 +... + q n) = bq, т.е. збирот a 1 + a 2 +… + a n испадна да биде претставен како производ на бројот b и некој природен број q. Тоа значи дека збирот a 1 + a 2 +... + a n е делив со b, што треба да се докаже.

На пример, без да правиме никакви пресметки, можеме да кажеме дека 175 + 360 + 915 е делив со 5, бидејќи секој член од оваа сума е делив со 5.

Теорема 6 (тест за деливост на разлика). Ако броевите a 1 и a 2 се делат со b и a 1 ≥ a 2, тогаш нивната разлика a 1 - a 2 се дели со b.

Доказот за оваа теорема е сличен на доказот за тестот за деливост за збир.

Теорема 7 (тест за деливост за производ). Ако бројот a е делив со b, тогаш производ од формата ax, каде што x Є N, се дели со b.

Доказ. Бидејќи а: . b, тогаш постои природен број q таков што а= bq. Ајде да ги помножиме двете страни на оваа еднаквост со природен број x. Потоа ax = (bq)x, од кое, врз основа на асоцијативното својство на множење, (bq)x = b(qx) и, според тоа, ax = b(qx), каде што qx е природен број. Според дефиницијата за односот на деливост, секира: . б, што требаше да се докаже.

Од докажаната теорема произлегува дека ако еден од множителите на производот е делив со природен број b, тогаш целиот производ е делив со b. На пример, производот 24 976 305 е делив со 12, бидејќи факторот 24 е делив со 12.

Да разгледаме уште три теореми поврзани со деливоста на збир и производ, кои често се користат при решавање на проблеми со деливост.

Теорема 8. Ако во збирот еден член не е делив со бројот b, а сите други членови се деливи со бројот b, тогаш целиот збир не е делив со бројот b.

Доказ. Нека s = a 1 + a g + ... + a n + "c и се знае дека a 1: . B, и 2: . B,

а 3: . b, ... и n:. б, но со: . б. Да докажеме дека тогаш е: . б

Да го претпоставиме спротивното, т.е. Нека: . б. Дозволете ни да го трансформираме збирот s во форма c = s- ( а 1 + а 2 +… + и n). Бидејќи с: . б по претпоставка, ( а 1 + а 2 +… + и n): . б според теоремата за деливост на збир, потоа со теоремата за деливост на разликата c: .б

Дојдовме до контрадикторност со даденото. Затоа, с:. б.

На пример, збирот 34 + 125 + 376 + 1024 не е делив со 2, така што 34: 0,2,376: ,2,124: ,2, но 125 не се дели со 2.

Теорема 9 . Ако во производот ab множителот асе дели со природниот број m, а факторот b се дели со природниот број n, а потоа ab се дели со mn.

Валидноста на оваа изјава произлегува од теоремата за деливост на производ.

Теорема 10.Доколку работата аке делив со производот bс, а c е природен број, тогаш Асе дели со b.

Доказ. Од кец акции на п.н.е.тогаш постои природен број q таков што ac = (bc)q, од каде ac = (bq)c и, според тоа, a = bq, т.е. А:.б.

Вежби

1. Објаснете зошто 15 е делител на 60, но не и 70.

2. Конструирај график на релацијата „да биде делител на даден број“ дадена на множеството X = (2, 6,. 12, 18, 24). Како својствата на оваа врска се рефлектираат на овој график?

3. Познато е дека бројот 24 е делител на бројот 96, а бројот 96 е делител на бројот 672. Докажи дека бројот 24 е делител на бројот 672 без да вршиш делење.

4. Запиши го множеството делители на бројот.

а) 24; 6)13; в) 1.

5 .На множеството X =(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11; 12) е дадена релацијата „да има ист број делители“. Дали е тоа еквивалентност?

6 .Направете заклучок со кој докажувате дека:

а) бројот 19 е прост;

б) бројот 22 е составен.

7. Докажете ги или побијте ги следните изјави:

а) Ако збирот на два члена е делив со одреден број, тогаш секој член е делив со овој број.

б) Ако еден од членовите на збирот не се дели со одреден број, тогаш збирот не се дели со овој број.

в) Ако ниту еден член не е делив со одреден број, тогаш збирот не се дели со овој број.

г) Ако еден од членовите на збирот се дели со одреден број, а другиот не се дели со овој број, тогаш збирот не се дели со овој број.

8. Дали е вистина дека:

а) а: . ty b: . n =>ab: .mn

б) a: .n и b: .n => ab: .n;

в) ab: .n => a: .n или b: .n.