Ако во училишниот курс по математика и алгебра одделно ја истакнеме темата „нееднаквост“, тогаш најчесто ќе ги научиме основите на работа со неравенки кои содржат променлива во нивната нотација. Во оваа статија ќе погледнеме што се неравенки со променливи, ќе кажеме како се нарекува нивното решение, а исто така ќе откриеме како се напишани решенијата на неравенките. За појаснување, ќе дадеме примери и потребни коментари.
Навигација на страницата.
Кои се неравенките со променливите?
На пример, ако неравенството нема решенија, тогаш тие пишуваат „нема решенија“ или го користат знакот за празно множество ∅.
Кога општото решение на неравенка е еден број, тогаш тој се пишува така, на пример, 0, −7,2 или 7/9, а понекогаш и тој е затворен во кадрави загради.
Ако решението на неравенството е претставено со неколку броеви и нивниот број е мал, тогаш тие едноставно се наведени одделени со запирки (или одделени со точка-запирка) или напишани одделени со запирки во загради. На пример, ако општото решение на неравенка со една променлива е три броја −5, 1,5 и 47, тогаш напишете −5, 1,5, 47 или (−5, 1,5, 47).
И за да напишат решенија на неравенки кои имаат бесконечен број решенија, тие ги користат и прифатените ознаки за множества природни, целобројни, рационални, реални броеви од формата N, Z, Q и R, ознаки за нумерички интервали и множества на поединечни броеви, наједноставните неравенки и опис на множество преку карактеристично својство и сите неименувани методи. Но, во пракса, најчесто се користат наједноставните неравенки и нумерички интервали. На пример, ако решението на неравенката е бројот 1, полуинтервалот (3, 7] и зракот, ∪; уредено од С. А. Телјаковски. - 16. издание - М.: Образование, 2008. - 271 стр. : лошо - ISBN 978-5-09-019243-9.
Видео лекцијата „Системи на неравенки со две променливи“ содржи визуелен едукативен материјал на оваа тема. Лекцијата вклучува разгледување на концептот за решавање на систем на неравенки со две променливи, примери за графичко решавање на такви системи. Целта на оваа видео лекција е да се развие способноста на учениците графички да решаваат системи на неравенки со две променливи, да го олеснат разбирањето на процесот на наоѓање решенија за такви системи и меморирање на методот на решение.
Секој опис на решението е придружен со цртежи кои го прикажуваат решението на проблемот на координатната рамнина. Ваквите бројки јасно ги покажуваат карактеристиките на конструирање графикони и локацијата на точките што одговараат на решението. Сите важни детали и концепти се означени со боја. Така, видео лекцијата е погодна алатка за решавање на проблемите на наставниците во училницата и го ослободува наставникот од презентирање стандарден блок материјал за индивидуална работа со учениците.
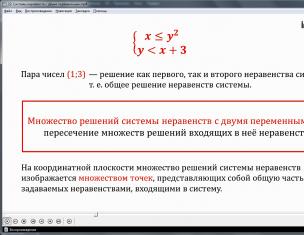
Видео лекцијата започнува со воведување на темата и разгледување на пример за наоѓање решенија за систем кој се состои од неравенки x<=y 2 и у<х+3. Примером точки, координаты которой удовлетворяют условиям обеих неравенств, является (1;3). Отмечается, что, так как данная пара значений является решением обоих неравенств, то она является одним из множества решений. А все множество решений будет охватывать пересечение множеств, которые являются решениями каждого из неравенств. Данный вывод выделен в рамку для запоминания и указания на его важность. Далее указывается, что множество решений на координатной плоскости представляет собой множество точек, которые являются общими для множеств, представляющих решения каждого из неравенств.

Разбирањето на заклучоците донесени за решавање на систем на нееднаквости се зајакнува со разгледување на примери. Прво се разгледува решението на системот на неравенки x 2 + y 2<=9 и x+y>=2. Очигледно, решенијата на првата неравенка на координатната рамнина го вклучуваат кругот x 2 + y 2 = 9 и регионот во него. Оваа област на сликата е исполнета со хоризонтално засенчување. Множеството решенија на неравенката x+y>=2 ја вклучува правата x+y=2 и полурамнината лоцирана горе. Оваа област е означена и на авионот со потези во различна насока. Сега можеме да го одредиме пресекот на две групи решенија на сликата. Тој е содржан во круг сегмент x 2 + y 2<=9, который покрыт штриховкой полуплоскости x+y>=2.
Следно, го анализираме решението на системот на линеарни неравенки y>=x-3 и y>=-2x+4. На сликата веднаш до условот за задача е конструирана координатна рамнина. На неа е изградена права линија која одговара на решенијата на равенката y=x-3. Областа на решение за неравенката y>=x-3 ќе биде плоштината што се наоѓа над оваа права. Таа е засенчена. Множеството решенија на втората неравенка се наоѓа над правата y=-2x+4. Оваа права линија е исто така изградена на истата координатна рамнина и површината на решението е изведена. Пресекот на две множества е аголот изграден од две прави линии, заедно со неговиот внатрешен регион. Областа на решението на системот на нееднаквости е исполнета со двојно засенчување.

Кога се разгледува третиот пример, се опишува случајот кога графиците на равенките што одговараат на неравенките на системот се паралелни прави. Потребно е да се реши системот на неравенки y<=3x+1 и y>= 3x-2. На координатната рамнина се конструира права линија што одговара на равенката y=3x+1. Опсег на вредности што одговараат на решенијата на неравенката y<=3x+1, лежит ниже данной прямой. Множество решений второго неравенства лежит выше прямой y=3x-2. При построении отмечается, что данные прямые параллельны. Область, являющаяся пересечением двух множеств решений, представляет собой полосу между данными прямыми.

Видео лекцијата „Системи на неравенки со две променливи“ може да се користи како визуелно помагало на лекција на училиште или да го замени објаснувањето на наставникот кога самостојно го проучувате материјалот. Детално, разбирливо објаснување за решавање на системи на неравенки на координатната рамнина може да помогне да се презентира материјалот за време на учење на далечина.
, и уште повеќе системи на неравенки со две променливи, се чинидоста тешка задача. Сепак, постои едноставен алгоритам кој помага лесно и без многу напор да се решат навидум многу сложени проблеми од овој вид. Ајде да се обидеме да го сфатиме.
Дозволете ни да имаме неравенство со две променливи од еден од следниве типови:
y > f(x); y ≥ f(x); y< f(x); y ≤ f(x).
За да го прикажете множеството решенија за таквата нееднаквост на координатната рамнина, постапете на следниов начин:
- Градиме график на функцијата y = f(x), која ја дели рамнината на два региони.
- Избираме која било од добиените области и разгледуваме произволна точка во неа. Ја проверуваме изводливоста на првобитната нееднаквост за оваа точка. Ако тестот резултира со правилна нумеричка неравенка, тогаш заклучуваме дека оригиналната неравенка е задоволена во целиот регион на кој припаѓа избраната точка. Така, множеството решенија на нееднаквоста е регионот на кој припаѓа избраната точка. Ако резултатот од проверката е неточна нумеричка неравенка, тогаш множеството решенија на неравенката ќе биде вториот регион на кој не припаѓа избраната точка.
- Ако неравенката е строга, тогаш границите на регионот, односно точките на графикот на функцијата y = f(x), не се вклучени во множеството решенија и границата е прикажана со точкаста линија. Ако неравенката не е строга, тогаш границите на регионот, односно точките на графикот на функцијата y = f(x), се вклучени во множеството решенија на оваа неравенка и границата во овој случај е прикажана како полна линија. Сега да разгледаме неколку проблеми на оваа тема.
Задача 1.
Кое множество точки е дадено со неравенката x · y ≤ 4?
Решение.
1) Градиме график на равенката x · y = 4. За да го направите ова, прво го трансформираме. Очигледно, x во овој случај не се претвора во 0, бидејќи во спротивно би имале 0 · y = 4, што е неточно. Ова значи дека можеме да ја поделиме нашата равенка со x. Добиваме: y = 4/x. Графикот на оваа функција е хипербола. Ја дели целата рамнина на два региони: оној помеѓу двете гранки на хиперболата и оној надвор од нив.
2) Да избереме произволна точка од првиот регион, нека биде точката (4; 2). Да ја провериме неравенството: 4 · 2 ≤ 4 – неточно.
Тоа значи дека точките од овој регион не ја задоволуваат првобитната нееднаквост. Тогаш можеме да заклучиме дека множеството решенија на неравенката ќе биде вториот регион на кој не му припаѓа избраната точка.
3) Бидејќи неравенството не е строга, граничните точки, односно точките на графикот на функцијата y=4/x ги цртаме со полна права.
Дозволете ни да го насликаме множеството точки што ја дефинираат првобитната нееднаквост со жолта боја (сл. 1).
Задача 2.
Нацртајте ја областа дефинирана на координатната рамнина од системот
Решение.
За почеток, градиме графикони на следните функции (сл. 2):
y = x 2 + 2 – парабола,
y + x = 1 – права линија
x 2 + y 2 = 9 – круг.

Сега да ја разгледаме секоја нееднаквост одделно.
1) y > x 2 + 2.
Ја земаме точката (0; 5), која се наоѓа над графикот на функцијата. Да ја провериме неравенството: 5 > 0 2 + 2 – точно.
Следствено, сите точки што лежат над дадената парабола y = x 2 + 2 ја задоволуваат првата неравенка на системот. Ајде да ги обоиме жолто.
2) y + x > 1.
Ја земаме точката (0; 3), која се наоѓа над графикот на функцијата. Да ја провериме неравенството: 3 + 0 > 1 – точно.
Следствено, сите точки што лежат над правата линија y + x = 1 ја задоволуваат втората нееднаквост на системот. Да ги обоиме со зелено засенчување.
3) x 2 + y 2 ≤ 9.
Ја земаме точката (0; -4), која лежи надвор од кругот x 2 + y 2 = 9. Ја проверуваме неравенството: 0 2 + (-4) 2 ≤ 9 – неточно.
Следствено, сите точки што лежат надвор од кругот x 2 + y 2 = 9 не ја задоволуваат третата нееднаквост на системот. Тогаш можеме да заклучиме дека сите точки што се наоѓаат во кругот x 2 + y 2 = 9 ја задоволуваат третата неравенка на системот. Ајде да ги обоиме со виолетово засенчување.

Не заборавајте дека ако нееднаквоста е строга, тогаш соодветната гранична линија треба да се повлече со точкаста линија. Ја добиваме следната слика (сл. 3).

Областа за пребарување е областа каде што сите три обоени области се вкрстуваат една со друга (сл. 4).
Прашања за белешки

Напиши неравенка чие решение е круг и точки во кругот: 
Најдете ги точките што ја решаваат неравенството:
1) (6;10)
2) (-12;0)
3) (8;9)
4) (9;7)
5) (-12;12)
Често е неопходно на координатната рамнина да се прикаже збир на решенија за неравенство со две променливи. Решение за неравенство во две променливи е пар вредности на овие променливи што ја претвора неравенката во вистинска нумеричка неравенка.
2у+ Zx< 6.
Прво, да изградиме права линија. За да го направите ова, ја запишуваме неравенката во форма на равенката 2у+ Zx = 6 и изразуваат y.Така, добиваме: y=(6-3x)/2.
Оваа линија го дели множеството од сите точки на координатната рамнина на точки лоцирани над неа и точки лоцирани под неа.
Земете мем од секоја област контролна точка, на пример A (1;1) и B (1;3)
Координатите на точката А ја задоволуваат оваа неравенка 2y + 3x< 6, т. е. 2 . 1 + 3 . 1 < 6.
Координати на точка Б Неја задоволува оваа неравенка 2∙3 + 3∙1< 6.
Бидејќи оваа неравенка може да го промени знакот на права линија 2y + 3x = 6, тогаш неравенството се задоволува со множеството точки во областа каде што се наоѓа точката А.
Така, го прикажавме множеството решенија за нееднаквоста 2y + Zx< 6.
Пример
Дозволете ни да го прикажеме множеството решенија на неравенката x 2 + 2x + y 2 - 4y + 1 > 0 на координатната рамнина.
Ајде прво да изградиме график на равенката x 2 + 2x + y 2 - 4y + 1 = 0. Да ја одделиме равенката на кругот во оваа равенка: (x 2 + 2x + 1) + (y 2 - 4y + 4) = 4, или (x + 1) 2 + (y - 2) 2 = 2 2 .
Ова е равенка на круг со центар во точката 0 (-1; 2) и радиус R = 2. Да ја конструираме оваа кружница.

Бидејќи оваа неравенка е строга и точките што лежат на самата кружница не ја задоволуваат неравенството, ние го конструираме кругот со точкаста линија.
Лесно е да се провери дали координатите на центарот О на кругот не ја задоволуваат оваа нееднаквост. Изразот x 2 + 2x + y 2 - 4y + 1 го менува својот знак на конструираната кружница. Тогаш неравенството се задоволува со точки лоцирани надвор од кругот. Овие точки се засенчени.
Пример
Дозволете ни да го прикажеме на координатната рамнина множеството решенија за неравенството
(y - x 2) (y - x - 3)< 0.
Прво, да изградиме график на равенката (y - x 2)(y - x - 3) = 0. Тоа е парабола y = x 2 и права линија y = x + 3. Да ги изградиме овие прави и да забележиме дека менувањето на знакот на изразот (y - x 2)(y - x - 3) се јавува само на овие прави. За точката А (0; 5), го одредуваме знакот на овој израз: (5- 3) > 0 (т.е. оваа неравенка не важи). Сега е лесно да се означи множеството точки за кои е задоволена оваа нееднаквост (овие области се засенчени).

Алгоритам за решавање на неравенки со две променливи
1. Да ја намалиме неравенството на формата f (x; y)< 0 (f (х; у) >0; f (x; y) ≤ 0; f (x; y) ≥ 0;)
2. Напиши ја еднаквоста f (x; y) = 0
3. Препознајте ги графиконите напишани на левата страна.
4. Ги градиме овие графикони. Ако неравенството е строга (f (x; y)< 0 или f (х; у) >0), тогаш - со цртички, ако неравенството не е строга (f (x; y) ≤ 0 или f (x; y) ≥ 0), тогаш - со полна линија.
5. Определи на колку делови од графиката е поделена координатната рамнина
6. Изберете контролна точка во еден од овие делови. Определи го знакот на изразот f (x; y)
7. Поставуваме знаци во други делови од рамнината, земајќи ја предвид алтернацијата (како со користење на методот интервал)
8. Ги избираме деловите што ни се потребни во согласност со знакот на нееднаквоста што го решаваме и применуваме засенчување
Тема: Равенки и неравенки. Системи на равенки и неравенки
Лекција:Равенки и неравенки со две променливи
Да разгледаме генерално равенка и неравенка со две променливи.
Равенка со две променливи;
Неравенство со две променливи, знакот за нееднаквост може да биде што било;
Овде x и y се променливи, p е израз кој зависи од нив
Пар од броеви () се нарекува делумно решение на таква равенка или неравенка ако, при замена на овој пар во изразот, ја добиеме точната равенка или неравенка, соодветно.
Задачата е да се најде или да се прикаже на рамнина множеството од сите решенија. Можете да ја парафразирате оваа задача - пронајдете го локусот на точки (GLP), конструирајте график на равенка или неравенка.
Пример 1 - реши равенка и неравенка:
Со други зборови, задачата вклучува наоѓање на GMT.
Да го разгледаме решението на равенката. Во овој случај, вредноста на променливата x може да биде која било, така што имаме:
Очигледно, решението на равенката е множеството точки што формираат права линија

Ориз. 1. График на равенки Пример 1
Решенијата на дадена равенка се, особено, точките (-1; 0), (0; 1), (x 0, x 0 +1)
Решението на дадената неравенка е полурамнина која се наоѓа над линијата, вклучувајќи ја и самата линија (види Слика 1). Навистина, ако земеме која било точка x 0 на правата, тогаш ја имаме еднаквоста . Ако земеме точка во полурамнина над права, имаме . Ако земеме точка во полурамнината под линијата, тогаш таа нема да ја задоволи нашата нееднаквост: .
Сега разгледајте го проблемот со круг и круг.
Пример 2 - реши равенка и неравенка:
Знаеме дека дадената равенка е равенка на круг со центар на почетокот и радиус 1.

Ориз. 2. Илустрација на пример 2
Во произволна точка x 0, равенката има две решенија: (x 0; y 0) и (x 0; -y 0).
Решението за дадена неравенка е збир на точки лоцирани во кругот, не земајќи го предвид самиот круг (види слика 2).
Да разгледаме равенка со модули.
Пример 3 - реши ја равенката:
Во овој случај, би било можно да се прошират модулите, но ќе ги разгледаме спецификите на равенката. Лесно е да се види дека графикот на оваа равенка е симетричен за двете оски. Тогаш, ако точката (x 0 ; y 0) е решение, тогаш точката (x 0 ; -y 0) е исто така решение, точките (-x 0 ; y 0) и (-x 0 ; -y 0 ) се исто така решение .
Така, доволно е да се најде решение каде што двете променливи се ненегативни и земаат симетрија за оските:

Ориз. 3. Илустрација на пример 3
Значи, како што гледаме, решението на равенката е квадрат.
Ајде да го разгледаме таканаречениот метод на област користејќи конкретен пример.
Пример 4 - прикажете го множеството решенија за неравенството:
Според методот на домени, најпрво ја разгледуваме функцијата од левата страна ако има нула од десната страна. Ова е функција од две променливи:
![]()
Слично на методот на интервали, привремено се оддалечуваме од нееднаквоста и ги проучуваме карактеристиките и својствата на составената функција.
ODZ: тоа значи дека оската x се пробива.
Сега означуваме дека функцијата е еднаква на нула кога броителот на дропката е еднаков на нула, имаме:
Градиме график на функцијата.

Ориз. 4. График на функцијата, земајќи го предвид ODZ
Сега разгледајте ги областите на постојан знак на функцијата, тие се формираат со права линија и скршена линија. внатре во скршената линија има област D 1. Помеѓу отсечка од скршена линија и права линија - област D 2, под линијата - област D 3, помеѓу отсечка на скршена линија и права линија - област D 4
Во секоја од избраните области, функцијата го задржува својот знак, што значи дека е доволно да се провери произволна точка за тестирање во секоја област.
Во областа ја земаме точката (0;1). Имаме:
![]()
Во областа ја земаме точката (10;1). Имаме:
![]()
Така, целиот регион е негативен и не ја задоволува дадената нееднаквост.
Во областа земете ја точката (0;-5). Имаме:
![]()
Така, целиот регион е позитивен и ја задоволува дадената нееднаквост.