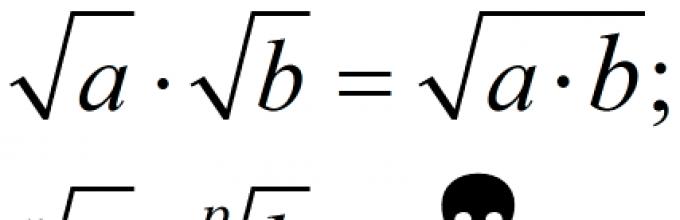n-тиот корен и неговите основни својства. Користење на својствата на корените при трансформација на ирационални изрази, примери, решенија Трансформирање изрази со броеви под знаците на корените

Повторно погледнав во знакот... И, одиме!

Да почнеме со нешто едноставно:

Само една минута. ова, што значи дека можеме да го напишеме вака:

Го сфативте? Еве го следниот за вас:

Дали корените на добиените броеви не се точно извлечени? Нема проблем - еве неколку примери:

Што ако нема два, туку повеќе множители? Истото! Формулата за множење на корените работи со кој било број фактори:

Сега целосно самостојно:

Одговори:Браво! Се согласувам, сè е многу лесно, главната работа е да се знае табелата за множење!

Поделба на коренот

Го средивме множењето на корените, сега да преминеме на својството на делење.

Да ве потсетам дека формулата во општ погледизгледа вака:

Што значи дека коренот на количникот е еднаков на количникот на корените.

Па, ајде да погледнеме неколку примери:

Тоа е сè што е науката. Еве еден пример:

Сè не е толку мазно како во првиот пример, но, како што можете да видите, нема ништо комплицирано.

Што ако наидете на овој израз:

Треба само да ја примените формулата во спротивна насока:

И еве еден пример:

Може да го сретнете и овој израз:

Сè е исто, само овде треба да запомните како да преведувате дропки (ако не се сеќавате, погледнете ја темата и вратете се!). Се сеќаваш ли? Сега да одлучиме!

Сигурен сум дека се справивте со сè, сега да се обидеме да ги подигнеме корените до степени.

Експоненцијација

Што се случува ако квадратниот корен е квадрат? Едноставно е, запомнете го значењето на квадратниот корен на број - ова е број чиј квадратен корен е еднаков на.

Значи, ако квадратиме број чиј квадратен корен е еднаков, што добиваме?

Па, се разбира!

Ајде да погледнеме примери:

Едноставно е, нели? Што ако коренот е во различен степен? Во ред е!

Следете ја истата логика и запомнете ги својствата и можните дејства со степени.

Прочитајте ја теоријата на темата „“ и сè ќе ви стане исклучително јасно.

На пример, еве еден израз:

Во овој пример, степенот е парен, но што ако е непарен? Повторно, примени ги својствата на моќите и факторирај сè:

Се чини дека сè е јасно со ова, но како да се извлече коренот на број во моќност? Еве, на пример, ова е:

Прилично едноставно, нели? Што ако степенот е поголем од два? Ја следиме истата логика користејќи ги својствата на степените:

Па, дали е сè јасно? Потоа сами решете ги примерите:

А еве ги одговорите:

Влегување под знакот на коренот

Што не научивме да правиме со корените! Останува само да вежбате да го внесете бројот под знакот за корен!

Навистина е лесно!

Да речеме дека имаме запишан број

Што можеме да правиме со тоа? Па, се разбира, скријте ги трите под коренот, сеќавајќи се дека трите е квадратниот корен на!

Зошто ни треба ова? Да, само за да ги прошириме нашите можности при решавање на примери:

Како ви се допаѓа ова својство на корените? Дали тоа многу го олеснува животот? За мене, тоа е точно! Само Мора да запомниме дека можеме да внесеме само позитивни броеви под знакот на квадратен корен.

Решете го овој пример сами -
Дали се снајде? Ајде да видиме што треба да добиете:

Браво! Успеавте да го внесете бројот под знакот за корен! Ајде да преминеме на нешто подеднакво важно - ајде да погледнеме како да споредиме броеви што содржат квадратен корен!

Споредба на корените

Зошто треба да научиме да споредуваме броеви што содржат квадратен корен?

Многу едноставно. Честопати, со големи и долги изрази што ги среќаваме на испитот, добиваме ирационален одговор (се сеќавате што е ова? Веќе разговаравме за ова денес!)

Добиените одговори треба да ги поставиме на координатната линија, на пример, за да одредиме кој интервал е погоден за решавање на равенката. И тука настанува проблемот: нема калкулатор на испитот, а без него како можете да замислите кој број е поголем, а кој помал? Тоа е тоа!

На пример, одреди што е поголемо: или?

Не можеш веднаш да кажеш. Па, ајде да го искористиме расклопуваното својство за внесување број под знакот за корен?

Потоа продолжи:

Па, очигледно, што поголем бројпод знакот на коренот, толку е поголем самиот корен!

Оние. ако, тогаш,.

Од ова цврсто заклучуваме дека. И никој нема да не убеди во спротивното!

Извлекување корени од голем број

Пред ова, внесовме множител под знакот на коренот, но како да го отстраниме? Вие само треба да го земете предвид и да го извлечете она што го извлекувате!

Беше можно да се земе поинаков пат и да се прошири во други фактори:

Не е лошо, нели? Било кој од овие пристапи е точен, одлучувајте како сакате.

Факторингот е многу корисен при решавање на такви нестандардни проблеми како што е овој:

Да не се плашиме, туку да дејствуваме! Ајде да го разложиме секој фактор под коренот на посебни фактори:

Сега пробајте сами (без калкулатор! Нема да биде на испит):

Дали е ова крајот? Да не застанеме на половина пат!

Тоа е сè, не е толку страшно, нели?

Дали тоа функционираше? Браво, така е!

Сега пробајте го овој пример:

Но, примерот е тврд орев за кршење, па не можете веднаш да сфатите како да му пристапите. Но, се разбира, можеме да се справиме со тоа.

Па, да почнеме со факторинг? Веднаш да забележиме дека можете да поделите број со (запомнете ги знаците на деливост):

Сега, обидете се сами (повторно, без калкулатор!):

Па, дали успеа? Браво, така е!

Ајде да го сумираме

1. Квадратниот корен (аритметички квадратен корен) на не негативен бројСе повикува ненегативен број чиј квадрат е еднаков на.
   .
2. Ако едноставно земеме квадратен корен од нешто, секогаш добиваме еден ненегативен резултат.
3. Својства на аритметички корен:
4. Кога се споредуваат квадратни коренипотребно е да се запамети дека колку е поголем бројот под знакот на коренот, толку е поголем самиот корен.

Како е квадратниот корен? Дали е се јасно?

Се обидовме без врева да ви објасниме се што треба да знаете на испитот за квадратниот корен.

Сега ти е редот. Пишете ни дали оваа тема ви е тешка или не.

Дали научи нешто ново или веќе се беше јасно?

Пишете во коментари и со среќа на вашите испити!

Поздрав, мачки! Последен пат детално разговаравме што се корените (ако не се сеќавате, препорачувам да го прочитате). Главното нешто од таа лекција: постои само една универзална дефиниција за корените, што е она што треба да го знаете. Останатото е глупост и губење време.

Денес одиме понатаму. Ќе научиме да множиме корени, ќе проучуваме некои проблеми поврзани со множењето (ако овие проблеми не се решат, тие можат да станат фатални на испитот) и ќе вежбаме правилно. Затоа, набавете пуканки, направете си удобност и ајде да започнеме :)

И ти уште не си го пушел, нели?

Лекцијата се покажа доста долга, па ја поделив на два дела:

1. Прво ќе ги разгледаме правилата за множење. Се чини дека капа навестува: ова е кога има два корени, меѓу нив има знак „множи“ - и сакаме да направиме нешто со него.
2. Потоа, да ја погледнеме спротивната ситуација: има еден голем корен, но ние бевме желни да го претставиме како производ на два поедноставни корени. Зошто е тоа потребно, е посебно прашање. Ќе го анализираме само алгоритмот.

За оние кои едвај чекаат веднаш да преминат на вториот дел, добредојдени сте. Да почнеме со останатите по ред.

Основно правило на множење

Да почнеме со наједноставната работа - класичните квадратни корени. Истите кои се означени со $\sqrt(a)$ и $\sqrt(b)$. Сè им е очигледно:

Правило за множење. За да помножите еден квадратен корен со друг, едноставно ќе ги помножите нивните радикални изрази и ќе го запишете резултатот под заедничкиот радикал:

\[\sqrt(a)\cdot \sqrt(b)=\sqrt(a\cdot b)\]

Не се наметнуваат дополнителни ограничувања на броевите од десната или левата страна: ако постојат коренските фактори, тогаш постои и производот.

Примери. Ајде да погледнеме четири примери со броеви одеднаш:

\[\begin(порамни) & \sqrt(25)\cdot \sqrt(4)=\sqrt(25\cdot 4)=\sqrt(100)=10; \\ & \sqrt(32)\cdot \sqrt(2)=\sqrt(32\cdot 2)=\sqrt(64)=8; \\ & \sqrt(54)\cdot \sqrt(6)=\sqrt(54\cdot 6)=\sqrt(324)=18; \\ & \sqrt(\frac(3)(17))\cdot \sqrt(\frac(17)(27))=\sqrt(\frac(3)(17)\cdot \frac(17)(27 ))=\sqrt(\frac(1)(9))=\frac(1)(3). \\ \крај (порамни)\]

Како што можете да видите, главната поента на ова правило е поедноставување ирационални изрази. И ако во првиот пример самите би ги извлекле корените на 25 и 4 без никакви нови правила, тогаш работите стануваат тешки: $\sqrt(32)$ и $\sqrt(2)$ не се сметаат сами по себе, туку нивниот производ се покажува како совршен квадрат, така што неговиот корен е еднаков на рационален број.

Особено би сакал да ја истакнам последната линија. Таму и двата радикални изрази се дропки. Благодарение на производот, многу фактори се откажани, а целиот израз се претвора во соодветен број.

Се разбира, работите нема секогаш да бидат толку убави. Понекогаш ќе има целосен хаос под корените - не е јасно што да се прави со него и како да се трансформира по множењето. Малку подоцна, кога ќе почнете да ги проучувате ирационалните равенки и неравенки, ќе има секакви променливи и функции. И многу често, пишувачите на проблеми сметаат на фактот дека ќе откриете некои поништувачки термини или фактори, по што проблемот ќе биде многукратно поедноставен.

Покрај тоа, воопшто не е неопходно да се множат точно два корени. Можете да помножите три, четири, па дури и десет одеднаш! Ова нема да го промени правилото. Погледнете:

\[\begin(порамни) & \sqrt(2)\cdot \sqrt(3)\cdot \sqrt(6)=\sqrt(2\cdot 3\cdot 6)=\sqrt(36)=6; \\ & \sqrt(5)\cdot \sqrt(2)\cdot \sqrt(0.001)=\sqrt(5\cdot 2\cdot 0.001)= \\ & =\sqrt(10\cdot \frac(1) (1000))=\sqrt(\frac(1)(100))=\frac(1)(10). \\ \крај (порамни)\]

И повторно мала забелешка за вториот пример. Како што можете да видите, во третиот фактор под коренот има децимална фракција - во процесот на пресметки ја заменуваме со редовна, по што сè лесно се намалува. Значи: Силно препорачувам да се ослободите од децималните фракции во какви било ирационални изрази (т.е. содржат барем еден радикален симбол). Ова ќе ви заштеди многу време и нерви во иднина.

Но, ова беше лирска дигресија. Сега да разгледаме еден поопшт случај - кога коренскиот експонент содржи произволен број $n$, а не само „класичните“ два.

Случај на произволен индикатор

Значи, ги подредивме квадратните корени. Што да се прави со кубните? Или дури и со корени од произволен степен $n$? Да, се е исто. Правилото останува исто:

За да се помножат два корени од степен $n$, доволно е да се помножат нивните радикални изрази, а потоа резултатот да се запише под еден радикал.

Во принцип, ништо комплицирано. Освен што износот на пресметките може да биде поголем. Ајде да погледнеме неколку примери:

Примери. Пресметајте ги производите:

\[\begin(порамни) & \sqrt(20)\cdot \sqrt(\frac(125)(4))=\sqrt(20\cdot \frac(125)(4))=\sqrt(625)= 5; \\ & \sqrt(\frac(16)(625))\cdot \sqrt(0,16)=\sqrt(\frac(16)(625)\cdot \frac(16)(100))=\sqrt (\ frac(64)(((25)^(2))\cdot 25))= \\ & =\sqrt(\frac(((4)^(3)))((25)^(3)) ))=\sqrt(((\left(\frac(4)(25) \десно))^(3)))=\frac(4)(25). \\ \крај (порамни)\]

И повторно, внимание на вториот израз. Ние множиме коцки корени, се ослободуваме децималнаи како резултат го добиваме производот од броевите 625 и 25 во именителот голем број- Лично, не можам веднаш да пресметам што е тоа еднакво.

Така, ние едноставно ја изолиравме точната коцка во броителот и именителот, а потоа употребивме едно од клучните својства (или, ако сакате, дефиниција) на $n$th корен:

\[\begin(порамни) & \sqrt(((a)^(2n+1)))=a; \\ & \sqrt(((a)^(2n)))=\лево| a\право|. \\ \крај (порамни)\]

Ваквите „махинации“ можат да ви заштедат многу време на испитот или тест работа, затоа запомнете:

Не брзајте да множите броеви користејќи радикални изрази. Прво, проверете: што ако точниот степен на кој било израз е „шифриран“ таму?

И покрај очигледноста на оваа забелешка, морам да признаам дека повеќето неподготвени студенти не ги гледаат точните степени во опсегот на точка-празно. Наместо тоа, тие множат сè целосно, а потоа се прашуваат: зошто добија толку брутални бројки :)

Сепак, сето ова е муабет за бебиња во споредба со она што сега ќе го проучуваме.

Множење корени со различни експоненти

Добро, сега можеме да множиме корени со истите показатели. Што ако индикаторите се различни? Да речеме, како да се помножи обичен $\sqrt(2)$ со некои глупости како $\sqrt(23)$? Дали е воопшто можно да се направи ова?

Да секако дека можеш. Сè е направено според оваа формула:

Правило за множење корени. За да се помножи $\sqrt[n](a)$ со $\sqrt[p](b)$, доволно е да се изврши следнава трансформација:

\[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p))\cdot ((b)^(n)))\]

Сепак, оваа формула функционира само ако радикалните изрази не се негативни. Ова е многу важна забелешка на која ќе се вратиме малку подоцна.

За сега, да погледнеме неколку примери:

\[\begin(порамни) & \sqrt(3)\cdot \sqrt(2)=\sqrt(((3)^(4))\cdot ((2)^(3)))=\sqrt(81 \cdot 8)=\sqrt(648); \\ & \sqrt(2)\cdot \sqrt(7)=\sqrt(((2)^(5))\cdot ((7)^(2))=\sqrt(32\cdot 49)= \sqrt(1568); \\ & \sqrt(5)\cdot \sqrt(3)=\sqrt(((5)^(4))\cdot ((3)^(2))=\sqrt(625\cdot 9)= \sqrt(5625). \\ \крај (порамни)\]

Како што можете да видите, ништо комплицирано. Сега да откриеме од каде е условот за негативност и што ќе се случи ако го прекршиме.

Умножувањето на корените е лесно

Зошто радикалните изрази мора да бидат ненегативни?

Секако дека можеш да бидеш како училишни наставниции паметно цитирај го учебникот:

Барањето за ненегативност е поврзано со различни дефинициикорени на парни и непарни степени (според тоа, нивните домени на дефиниција се исто така различни).

Па, дали стана појасно? Лично, кога ја прочитав оваа глупост во 8-мо одделение, разбрав нешто како следново: „Барањето за ненегативност се поврзува со *#&^@(*#@^#)~%“ - накратко, не Не разбирам проклето нешто во тоа време :)

Па сега ќе објаснам сè на нормален начин.

Прво, да дознаеме од каде доаѓа формулата за множење погоре. За да го направите ова, дозволете ми да ве потсетам на едно важно својство на root:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Со други зборови, можеме безбедно да го подигнеме радикалниот израз на која било природна моќност $k$ - во овој случај, експонентот на коренот ќе треба да се помножи со истата моќност. Затоа, лесно можеме да ги намалиме сите корени на заеднички експонент, а потоа да ги умножиме. Оттука доаѓа формулата за множење:

\[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p)))\cdot \sqrt(((b)^(n)))= \sqrt(((a)^(p))\cdot ((b)^(n)))\]

Но, постои еден проблем што остро ја ограничува употребата на сите овие формули. Размислете за овој број:

Според формулата штотуку дадена, можеме да додадеме кој било степен. Ајде да се обидеме да додадеме $k=2$:

\[\sqrt(-5)=\sqrt(((\лево(-5 \десно))^(2)))=\sqrt(((5)^(2)))\]

Го отстранивме минусот токму затоа што квадратот го согорува минусот (како и секој друг парен степен). Сега ајде да го направиме тоа инверзна конверзија: „намали“ два во експонент и моќност. На крајот на краиштата, секоја еднаквост може да се чита и од лево кон десно и од десно кон лево:

\[\почеток(порамни) & \sqrt[n](a)=\sqrt(((a)^(k)))\Десна стрелка \sqrt(((a)^(k)))=\sqrt[n ](а); \\ & \sqrt(((a)^(k)))=\sqrt[n](a)\десна стрелка \sqrt(((5)^(2))=\sqrt(((5)^( 2)))=\sqrt (5). \\ \крај (порамни)\]

Но, тогаш испаѓа дека е некаква глупост:

\[\sqrt(-5)=\sqrt(5)\]

Ова не може да се случи, бидејќи $\sqrt(-5) \lt 0$ и $\sqrt(5) \gt 0$. Ова значи дека за парни сили и негативни броеви нашата формула повеќе не работи. После тоа имаме две опции:

1. Да се ​​удри во ѕид и да се каже дека математиката е глупава наука, каде што „има некои правила, но тие се непрецизни“;
2. Воведете дополнителни ограничувања според кои формулата ќе стане 100% функционална.

Во првата опција, ќе мораме постојано да фаќаме „неработни“ случаи - тоа е тешко, одзема време и генерално е уф. Затоа, математичарите ја претпочитаа втората опција :)

Но, не грижете се! Во пракса, ова ограничување на кој било начин не влијае на пресметките, бидејќи сите опишани проблеми се однесуваат само на корените од непарен степен, а од нив може да се земат минусите.

Затоа, да формулираме уште едно правило, кое генерално важи за сите дејства со корени:

Пред да множите корени, проверете дали радикалните изрази се не-негативни.

Пример. Во бројот $\sqrt(-5)$ можете да го отстраните минусот под знакот за корен - тогаш сè ќе биде нормално:

\[\begin(порамни) & \sqrt(-5)=-\sqrt(5) \lt 0\Десна стрелка \\ & \sqrt(-5)=-\sqrt(((5)^(2))) =-\sqrt(25)=-\sqrt(((5)^(2)))=-\sqrt(5) \lt 0 \\ \крај (порамни)\]

Дали ја чувствувате разликата? Ако оставите минус под коренот, тогаш кога радикалниот израз е на квадрат, тој ќе исчезне и ќе започне глупост. И ако прво го извадите минусот, тогаш можете да го изградите/отстранете квадратот додека не станете сини во лицето - бројот ќе остане негативен.

Така, најточниот и најсигурен начин за размножување на корените е како што следува:

1. Отстранете ги сите негативни од радикалите. Минусите постојат само во корените со непарна мноштво - тие можат да се постават пред коренот и, доколку е потребно, да се намалат (на пример, ако има два од овие минуси).
2. Изведете множење според правилата дискутирани погоре во денешната лекција. Ако индикаторите на корените се исти, едноставно ги множиме радикалните изрази. И ако тие се различни, ја користиме злобната формула \[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p))\cdot ((b) ^(n) ))\].
3. 3.Уживајте во резултатот и добрите оценки.:)

Па? Да вежбаме?

Пример 1: Поедноставете го изразот:

\[\begin(порамни) & \sqrt(48)\cdot \sqrt(-\frac(4)(3))=\sqrt(48)\cdot \left(-\sqrt(\frac(4)(3 ) )) \десно)=-\sqrt(48)\cdot \sqrt(\frac(4)(3))= \\ & =-\sqrt(48\cdot \frac(4)(3))=- \ sqrt(64)=-4; \крај (порамни)\]

Ова е наједноставната опција: корените се исти и чудни, единствениот проблем е што вториот фактор е негативен. Овој минус го вадиме од сликата, по што сè лесно се пресметува.

Пример 2: Поедноставете го изразот:

\[\begin(порамни) & \sqrt(32)\cdot \sqrt(4)=\sqrt(((2)^(5)))\cdot \sqrt(((2)^(2))= \sqrt(((\лево(((2)^(5)) \десно))^(3))\cdot ((\лево(((2)^(2)) \десно))^(4) ))= \\ & =\sqrt(((2)^(15))\cdot ((2)^(8)))=\sqrt(((2)^(23))) \\ \end( порамни)\]

Многумина овде би биле збунети од она што се случи на крајот ирационален број. Да, тоа се случува: не можевме целосно да се ослободиме од коренот, но барем значително го поедноставивме изразот.

Пример 3: Поедноставете го изразот:

\[\begin(порамни) & \sqrt(a)\cdot \sqrt(((a)^(4)))=\sqrt(((a)^(3))\cdot ((\left((( a)^(4)) \десно))^(6))=\sqrt(((a)^(3))\cdot ((a)^(24))) = \\ & =\sqrt( ((a)^(27)))=\sqrt(((a)^(3\cdot 9)))=\sqrt(((a)^(3))) \end(порамни)\]

Би сакал да го привлечам вашето внимание на оваа задача. Тука има две точки:

1. Коренот не е одреден број или моќност, туку променливата $a$. На прв поглед, ова е малку необично, но во реалноста, кога се решава математички проблемиНајчесто ќе треба да се справите со променливи.
2. На крајот успеавме да го „намалиме“ радикалниот индикатор и степенот на радикално изразување. Ова се случува доста често. И ова значи дека беше можно значително да се поедностават пресметките ако не ја користевте основната формула.

На пример, можете да го направите ова:

\[\begin(порамни) & \sqrt(a)\cdot \sqrt(((a)^(4)))=\sqrt(a)\cdot \sqrt(((\left(((a)^( 4)) \десно))^(2))=\sqrt(a)\cdot \sqrt((a)^(8))) \\ & =\sqrt(a\cdot ((a)^( 8)))=\sqrt(((a)^(9)))=\sqrt(((a)^(3\cdot 3)))=\sqrt(((a)^(3))) \ \\крај (порамни)\]

Всушност, сите трансформации беа извршени само со вториот радикал. И ако не ги опишете детално сите средни чекори, тогаш на крајот износот на пресметките значително ќе се намали.

Всушност, веќе наидовме на слична задача погоре кога го решивме примерот $\sqrt(5)\cdot \sqrt(3)$. Сега може да се напише многу поедноставно:

\[\begin(порамни) & \sqrt(5)\cdot \sqrt(3)=\sqrt(((5)^(4))\cdot ((3)^(2)))=\sqrt(( (\лево(((5)^(2))\cточка 3 \десно))^(2))= \\ & =\sqrt(((\лево(75 \десно))^(2))) =\sqrt (75). \крај (порамни)\]

Па, го средивме множењето на корените. Сега да ја разгледаме обратната операција: што да правиме кога има производ под коренот?

Материјалот во оваа статија треба да се смета како дел од темата трансформација на ирационални изрази. Овде ќе користиме примери за да ги анализираме сите суптилности и нијанси (од кои има многу) што се појавуваат при извршување на трансформации врз основа на својствата на корените.

Навигација на страницата.

Да се ​​потсетиме на својствата на корените

Бидејќи ќе се занимаваме со трансформација на изразите користејќи ги својствата на корените, нема да биде лошо да ги запомните главните, или уште подобро, да ги запишете на хартија и да ги поставите пред вас.

Прво проучен квадратни корении нивните следни својства (a, b, a 1, a 2, ..., a k се реални броеви):

И подоцна се проширува идејата за корен, се воведува дефиниција за корен од n-ти степен и се разгледуваат следните својства (a, b, a 1, a 2, ..., a k се реални броеви, m, n, n 1, n 2, ... , n k - природни броеви):

Конвертирање на изрази со броеви под радикални знаци

Како и обично, прво учат да работат со нумерички изрази, па дури потоа преминуваат на изрази со променливи. Ние ќе го сториме истото, а прво ќе се занимаваме со трансформација на ирационални изрази кои содржат само нумерички изрази, а потоа во следниот пасус ќе воведеме променливи под знаците на корените.

Како може ова да се искористи за трансформирање на изрази? Многу е едноставно: на пример, можеме да замениме ирационален израз со израз или обратно. Односно, ако изразот што се конвертира содржи израз кој по изглед се совпаѓа со изразот од левиот (десниот) дел на кое било од наведените својства на корените, тогаш тој може да се замени со соодветниот израз од десниот (лев) дел. Ова е трансформација на изразите користејќи ги својствата на корените.

Да дадеме уште неколку примери.

Ајде да го поедноставиме изразот . Броевите 3, 5 и 7 се позитивни, така што можеме безбедно да ги примениме својствата на корените. Овде можете да дејствувате на различни начини. На пример, коренот заснован на својство може да се претстави како , а коренот кој користи својство со k=3 - како , со овој пристап решението ќе изгледа вака:

Може да се направи поинаку со замена со , а потоа со , во кој случај решението би изгледало вака:

Можни се и други решенија, на пример:

Да го погледнеме решението на друг пример. Ајде да го трансформираме изразот. Гледајќи го списокот со својства на корените, од него ги избираме својствата што ни се потребни за да го решиме примерот, јасно е дека две од нив се корисни овде и , кои се валидни за секој a . Имаме:

Алтернативно, прво може да се трансформираат радикалните изрази користејќи

а потоа се применуваат својствата на корените

До овој момент, ние конвертиравме изрази кои содржат само квадратни корени. Време е да се работи со корени кои имаат различни индикатори.

Пример.

Претворете го ирационалниот израз .

Решение.

По имот првиот фактор на даден производ може да се замени со бројот -2:

Да продолжиме понатаму. Врз основа на својството, вториот фактор може да се претстави како , и не би било лошо да се замени 81 со четирикратна моќност од три, бидејќи во останатите фактори бројот 3 се појавува под знаците на корените:

Препорачливо е да се замени коренот на фракција со сооднос на корените на формата, што може дополнително да се трансформира: . имаме

По извршувањето на операциите со двојки, добиениот израз ќе добие форма , а останува само да се трансформира производот на корените.

За да се трансформираат производите од корени, тие обично се сведуваат на еден индикатор, за што е препорачливо да се земат индикаторите за сите корени. Во нашиот случај, LCM(12, 6, 12) = 12, и само коренот ќе треба да се сведе на овој индикатор, бидејќи другите два корени веќе имаат таков индикатор. Еднаквоста, која се применува од десно кон лево, ни овозможува да се справиме со оваа задача. Значи . Земајќи го предвид овој резултат, имаме

Сега производот од корените може да се замени со коренот на производот и да се извршат преостанатите, веќе очигледни, трансформации:

Ние ќе издадеме кратка верзијарешенија:

Одговор:

.

Посебно нагласуваме дека за да се применат својствата на корените, потребно е да се земат предвид ограничувањата наметнати на броевите под знаците на корените (a≥0 итн.). Игнорирањето на истите може да предизвика неточни резултати. На пример, знаеме дека својството важи за не-негативни a . Врз основа на него, лесно можеме да се движиме, на пример, од до, бидејќи 8 е позитивен број. Но, ако земеме значаен корен од негативен број, на пример, и, врз основа на горенаведеното својство, го замениме со , тогаш всушност го заменуваме −2 со 2. Навистина, ах. Односно, за негативното a еднаквоста може да биде неточна, исто како што другите својства на корените може да бидат неточни без да се земат предвид условите наведени за нив.

Но, она што беше кажано во претходниот пасус воопшто не значи дека изразите со негативни броеви под знаците на корените не можат да се трансформираат користејќи ги својствата на корените. Тие само треба да се „подготват“ прво со примена на правилата за работа со броеви или со користење на дефиницијата за непарен корен од негативен број, што одговара на еднаквоста , каде што −a е негативен број (додека a е позитивен). На пример, не може веднаш да се замени со , бидејќи −2 и −3 се негативни броеви, но ни овозможува да се движиме од коренот во , а потоа дополнително да го примениме својството на коренот на производот: . И во еден од претходните примери, требаше да се движи од корен до корен од осумнаесеттиот степен не вака, туку вака .

Значи, за да ги трансформирате изразите користејќи ги својствата на корените, ви треба

• изберете го соодветното својство од списокот,
• проверете дали броевите под коренот ги задоволуваат условите за избраното својство (во спротивно треба да извршите прелиминарни трансформации),
• и да се изврши планираната трансформација.

Конвертирање на изрази со променливи под радикални знаци

За да се трансформираат ирационални изрази што содржат не само броеви, туку и променливи под знакот на коренот, мора внимателно да се применат својствата на корените наведени во првиот став од овој член. Ова најмногу се должи на условите што мора да ги задоволат броевите вклучени во формулите. На пример, врз основа на формулата, изразот може да се замени со израз само за оние вредности на x кои ги задоволуваат условите x≥0 и x+1≥0, бидејќи наведената формула е наведена за a≥0 и b ≥0.

Кои се опасностите од игнорирањето на овие услови? Одговорот на ова прашање е јасно прикажан со следниот пример. Да речеме дека треба да ја пресметаме вредноста на изразот на x=−2. Ако веднаш го замениме бројот −2 наместо променливата x, ќе ја добиеме вредноста што ни треба . Сега да замислиме дека, врз основа на некои размислувања, го конвертиравме дадениот израз во форма и дури после тоа решивме да ја пресметаме вредноста. Бројот −2 го заменуваме со x и доаѓаме до изразот , што нема смисла.

Ајде да видиме што се случува со опсегот на дозволени вредности (APV) на променливата x кога се движите од израз до израз. Не случајно го спомнавме ОДЗ, бидејќи ова е сериозна алатка за следење на допуштеноста на направените трансформации, а промената на ОДЗ по трансформација на израз треба, во најмала рака, да крева црвени знамиња. Не е тешко да се најде ODZ за овие изрази. За изразот на ODZ се одредува од неравенката x·(x+1)≥0, неговото решение дава множество на броеви (−∞, −1]∪∪∪}