Договор за користење на материјалите на локацијата
Ве молиме да ги користите делата објавени на страницата исклучиво за лични цели. Забрането е објавување материјали на други сајтови.
Ова дело (и сите други) е достапно за преземање потполно бесплатно. Можете ментално да му се заблагодарите на неговиот автор и тимот на страницата.
Испратете ја вашата добра работа во базата на знаење е едноставна. Користете ја формата подолу
Студентите, дипломираните студенти, младите научници кои ја користат базата на знаење во нивните студии и работа ќе ви бидат многу благодарни.
Слични документи
Собирање и множење на p-адични цели броеви, дефинирани како собирање по член по член и множење на низи. Прстен од p-адични цели броеви, проучување на својствата на нивната поделба. Објаснување на дадени броеви со воведување на нови математички предмети.
работа на курсот, додадена 22.06.2015
Како луѓето научиле да бројат, појавата на броеви, броеви и системи на броеви. Табела за множење на „прстите“: техника за множење за броевите 9 и 8. Примери за брзо броење. Начини за множење на двоцифрен број со 11, 111, 1111 итн. и трицифрен број за 999.
работа на курсот, додадена на 22.10.2011 година
Нов начин за множење броеви. Сличноста помеѓу матрицата на броеви формирана при пресметувањето и триаголникот е релативна, но сепак постои, особено кога се множат трицифрени броеви и повисоки. Триаголна матрица.
статија, додадена на 06.02.2005 година
апстракт, додаден на 13.01.2011 година
Карактеристики на историјата на проучување на значењето на простите броеви во математиката со опишување методи за нивно пронаоѓање. Придонесот на Пјетро Каталди во развојот на теоријата на прости броеви. Методот на Ератостен за составување табели на прости броеви. Пријателство на природните броеви.
тест, додаден на 24.12.2010 година
Множеството од ненегативни реални броеви како интерпретабилно подмножество на R. Деливост во мултипликативни полугрупи. Структура на нумерички gcds и lcds на полугрупи. Проучување на мултипликативни полугрупи на ненегативни реални броеви со 0 и 1.
теза, додадена 27.05.2008
Својства на реалните броеви, нивната улога во развојот на математиката. Анализа на конструкцијата на множеството реални броеви од историски аспект. Пристапи кон конструирање на теоријата на реални броеви според Кантор, Вајерштрас, Дедекинд. Нивното учење во училишниот курс.
презентација, додадена 10/09/2011
Примарни елементи на математиката. Својства на природните броеви. Концептот на теоријата на броеви. Општи својства на споредбите и алгебарските равенки. Аритметички операции со споредби. Основни закони на аритметиката. Проверка на резултатите од аритметички операции.
работа на курсот, додадена 15.05.2015
Како основен концепт кога
аксиоматска конструкција на аритметиката
природните броеви го земаат односот
„директно следете“ дадено на
непразен сет Н.
Елементот веднаш следен
елемент a, означете a."
ниту елемент кој не следи веднаш
зад кој елемент на оваа гарнитура. Ние ќе
наречете го единица.
Аксиома 2. За секој елемент a од N
има само еден елемент а“,
веднаш по а. Аксиома 3. За секој елемент a од N
има најмногу еден елемент по
по што веднаш следи а.
Аксиома 4. Секое подмножество на М
множеството N ги има следните својства:
1) единицата припаѓа на множеството М;
2) од тоа што а е содржано во М, произлегува дека
дека а“ е содржано во М, тогаш М се совпаѓа со
сет Н.
Дефиниција на природен број
Множество N, за чии елементи е воспоставена релацијата„директно следете“, задоволувајќи ги аксиоми 1-4,
се нарекува множество природни броеви, а неговите елементи се природни броеви.
Додаток
Дефиниција. Собирањето на природните броеви се нарекуваалгебарска операција со следните својства:
1) (Ɐa ∈ N) a + 1 = a",
2) (Ɐa, b ∈ N) a + b"=(a+b)".
Бројот a+b се нарекува збир на броевите a и b, и самите броеви a и b
услови.
Дозволете ни да се договориме за следната нотација:
1" = 2; 2" = 3; 3" = 4; 4" = 5, итн.
Својства на додавање
Теорема 3. Собирање на природни броеви постои и тоасамо
Теорема 4. (Ɐ a, b, c ∈ N)(a + b) + c = a + (b + c)
Теорема 5. (Ɐ a, b ∈ N) a+b = b+a
Множење
Множењето на природните броеви се нарекува алгебарскооперација со следниве својства:
1)(Ɐ a ∈ N) a·1 =a;
2)(Ɐ a, b ∈ N) a·b" = a·b + a.
Бројот a b се нарекува производ на броевите a и b, а самите броеви a и
б - множители
Својства на множење
Теорема 7. Множење на природните броеви постои, и тоасамо.
Теорема 8. (Ɐ a, b, c ∈ N)(a + b) c = ac + b c - дистрибутивност
десно во однос на собирањето.
Теорема 9. (Ɐ a, b, c ∈ N) a·(b + c) = + a·c - лева дистрибутивност
во врска со додавањето.
Теорема 10. (Ɐ a, b, c ∈ N) (a b) c = a (b c) - асоцијативност
множење.
Теорема 11. (Ɐ a, b ∈ N) a·b = a·b - комутативност на множење
Прашања за самотестирање
1. Дали аксиомата 3 може да се формулира на следниов начин: „За секој елемента од N постои единствен елемент веднаш проследен со
треба да „?
2. Продолжи со дефиницијата за природен број: „Природен број
се нарекува елемент на множеството...“
3. Дали е точно дека секој природен број се добива од претходниот?
со додавање на еден?
4. Кои својства на множење може да се користат при наоѓање
значења на изразот:
а) 5·(10 + 4); б) 125·15·6; в) (8·379)·125?
Литература
Стоилова Л.П.Математика: Учебник за ученици. повисоко пед. тетратка претпријатија.
М.: Издавачки центар „Академија“. 2002. - 424 стр.
Аксиоматски метод во математиката.
Основни поими и односи на аксиоматската теорија на природните серии. Дефиниција на природен број.
Собирање на природни броеви.
Множење на природни броеви.
Својства на множеството природни броеви
Одземање и делење на природни броеви.
Аксиоматски метод во математиката
Во аксиоматската конструкција на која било математичка теорија, се почитуваат следниве правила: одредени правила:
1. Некои концепти на теоријата се избрани како главени се прифаќаат без дефиниција.
2. Се формулираат аксиоми, кои во оваа теорија се прифатени без доказ, ги откриваат својствата на основните поими.
3. Даден е секој концепт на теоријата што не е содржан во листата на основни дефиниција, го објаснува неговото значење со помош на главните и претходните концепти.
4. Секој предлог на теорија што не е содржан во списокот на аксиоми мора да се докаже. Ваквите предлози се нарекуваат теоремии да ги докаже врз основа на аксиоми и теореми кои претходат на разгледуваната.
Системот на аксиомите треба да биде:
а) доследна:мора да бидеме сигурни дека, извлекувајќи ги сите можни заклучоци од даден систем на аксиоми, никогаш нема да дојдеме до противречност;
б) независни: ниту една аксиома не треба да биде последица на други аксиоми на овој систем.
V) полн, ако во нејзините рамки секогаш е можно да се докаже или дадена изјава или нејзина негација.
Првото искуство на конструкцијата на аксиоматската теорија може да се смета за презентација на геометријата од Евклид во неговите „Елементи“ (3 век п.н.е.). Значаен придонес во развојот на аксиоматскиот метод на градење геометрија и алгебра дал Н.И. Лобачевски и Е. Галоа. На крајот на 19 век. Италијанскиот математичар Пеано разви систем на аксиоми за аритметика.
Основни поими и односи на аксиоматската теорија на природните броеви. Дефиниција на природен број.
Како основен (недефиниран) концепт во одредено множество Н е избрано став , а исто така користи и теоретски концепти на множества, како и правила на логика.
Елементот веднаш по елементот А,означуваат А“.
Односот „директно следење“ ги задоволува следните аксиоми:
Аксиоми на Пеано:
Аксиома 1. Во изобилство Н има елемент директно не следноне за кој било елемент од овој сет. Ајде да му се јавиме единицаи се означува со симболот 1 .
Аксиома 2. За секој елемент А од Н има само еден елемент А" , веднаш потоа А .
Аксиома 3. За секој елемент А од Нима најмногу еден елемент кој веднаш е проследен со А .
Аксиома 4.Секое подмножество М множества Н се совпаѓа со Н , ако ги има следните својства: 1) 1 содржани во М ; 2) од фактот дека А содржани во М , го следи тоа А" содржани во М.
Дефиниција 1. Еден куп Н , за чии елементи се воспоставува релацијата „директно следете“, се нарекува задоволување на аксиомите 1-4 збир на природни броеви, а неговите елементи се природни броеви.
Оваа дефиниција не кажува ништо за природата на елементите на множеството Н . Значи, може да биде се. Избор како сет Н одредено множество на кое е дадена специфична релација „директно следи“, задоволувајќи ги аксиомите 1-4, добиваме модел на овој систем аксиома.
Стандардниот модел на системот за аксиома Пеано е серија од броеви кои се појавија во процесот на историскиот развој на општеството: 1,2,3,4,... Природната серија започнува со бројот 1 (аксиома 1); по секој природен број веднаш следи еден природен број (аксиома 2); секој природен број веднаш следи најмногу еден природен број (аксиома 3); поаѓајќи од бројот 1 и движејќи се кон природните броеви веднаш по еден по друг, го добиваме целото множество од овие броеви (аксиома 4).
Значи, ја започнавме аксиоматската конструкција на систем на природни броеви со избирање на основните односот „директно следење“.и аксиоми кои ги опишуваат неговите својства. Понатамошната конструкција на теоријата вклучува разгледување на познатите својства на природните броеви и операциите на нив. Тие мора да бидат обелоденети во дефиниции и теореми, т.е. се изведени чисто логички од релацијата „директно следат“, и аксиоми 1-4.
Првиот концепт што ќе го воведеме по дефинирањето на природен број е став „веднаш претходи“ , што често се користи кога се разгледуваат својствата на природната серија.
Дефиниција 2.Ако природен број б директно следиприроден број А, тој број А повикани веднаш пред(или претходно) број б .
Релацијата „претходи“ има голем број на имоти.
Теорема 1. Единицата нема претходен природен број.
Теорема 2. Секој природен број А, освен 1, има еден претходен број б,такви што б"= А.
Аксиоматската конструкција на теоријата на природни броеви не се разгледува ниту во основните ниту во средните училишта. Меѓутоа, оние својства на релацијата „директно следат“, кои се рефлектираат во аксиомите на Пеано, се предмет на проучување во почетниот курс по математика. Веќе во прво одделение, кога се разгледуваат броевите на првите десет, станува јасно како може да се добие секој број. Се користат концептите „следи“ и „претходи“. Секој нов број делува како продолжение на проучуваниот сегмент од природната серија на броеви. Учениците се убедени дека секој број го следи следниот, а згора на тоа, само едно нешто, дека природната серија на броеви е бесконечна.
Собирање на природни броеви
Според правилата за конструирање на аксиоматска теорија, дефиницијата за собирање на природни броеви мора да се воведе со користење само на релацијата „директно следете“, и концепти „природен број“И „претходен број“.
Да ја предговориме дефиницијата за собирање со следните размислувања. Ако на кој било природен број Адодадете 1, го добиваме бројот А",веднаш потоа А, т.е. А+ 1= а"и затоа го добиваме правилото за собирање 1 на кој било природен број. Но, како да се додаде на број Априроден број б,различен од 1? Да го искористиме следниов факт: ако знаеме дека 2 + 3 = 5, тогаш збирот е 2 + 4 = 6, што веднаш следи по бројот 5. Ова се случува затоа што во збирот 2 + 4 вториот член е бројот веднаш по бројот 3. Така, 2 + 4 =2+3 " =(2+3)". Во принцип имаме , .
Овие факти ја формираат основата за дефиницијата за собирање на природни броеви во аксиоматската теорија.
Дефиниција 3. Собирање на природни броевие алгебарска операција која ги има следните својства:
Број a + b повикани збир на броеви АИ б , и самите бројки АИ б - услови.
Кога аксиоматски се конструира теорија, се следат одредени правила:
се избираат некои концепти на теоријата како основни,а се прифаќаат без дефиниција и се нарекуваат неопределени.
се формулираат аксиоми - предлози кои во дадена теорија се прифаќаат без доказ; ги откриваат својствата на основните поими;
даден е секој концепт на теоријата што не е содржан во листата на основни дефиниција, го објаснува своето значење со помош на основните и претходните поими;
мора да се докаже секој предлог на теорија што не е содржан во списокот на аксиоми; таквите предлози се нарекуваат теореми и се докажуваат врз основа на аксиоми и теореми кои претходат на разгледуваниот.
Во аксиоматската конструкција на теоријата, во суштина сите искази се изведени со доказ од аксиоми. Затоа, посебни барања се поставуваат на аксиомскиот систем. Пред сè, тој мора да биде конзистентен и независен.
Системот на аксиоми се нарекува конзистентна,ако од него не можат логички да се извлечат две меѓусебно исклучувачки реченици.
Конзистентен систем на аксиоми се нарекува независна,ако ниту една од аксиомите на овој систем не е последица на другите аксиоми на овој систем.
Аксиомите, по правило, се одраз на вековните практични активности на луѓето и тоа ја одредува нивната валидност.
Како основен концепт во аксиоматската конструкција на аритметиката на природните броеви, земена е релацијата „директно следи“, дефинирана на непразно множество. Н.За познати се и концептите на множество, елемент на множество и други теоретски концепти на множества, како и правилата на логиката.
Елементот веднаш по елементот А,означуваат А“.Суштината на односот „директно следење“ се открива во следните аксиоми, предложени од италијанскиот математичар Г. Пеано во 1891 година.
Аксиома 1.Во изобилство Нпостои елемент кој веднаш не следи ниту еден елемент од ова множество. Се нарекува единица и се означува со симболот 1.
Аксиома 2.За секој елемент Аод Нима само еден елемент А",веднаш потоа А.
Аксиома 3.За секој елемент a од Нима најмногу еден елемент кој веднаш е проследен со А.
Аксиома 4. (Аксиома на индукција).Секое подмножество Ммножества Нсе совпаѓа со N ако ги има следните својства: 1) 1 се содржи во М; 2) од фактот дека кој било елемент Асодржани во М,го следи тоа А"содржани во М.
Формулираните аксиоми често се нарекуваат аксиоми на Пеано, а четвртата аксиома се нарекува аксиома на индукција.
Да ги напишеме овие аксиоми во симболична форма.
А 1 )( 1 Н)( а N)А" 1;
А 2 )( а Н)( !б N)А"=б
А 3 ) ( А,б,Со Н)c = a" c = b" А= b;
А 4) М Н 1 М (а М А" М) М=Н
Користејќи ја релацијата „веднаш следи“ и аксиомите на Пеано 1-4, можеме да ја дадеме следната дефиниција за природен број.
Дефиниција 1. Множеството N. за чии елементи е воспоставена релацијата „директно следи“, задоволувајќи ги аксиомите 1-4, се нарекува множество природни броеви, а неговите елементи природни броеви.
___________________________________________________________________
Дефиниција 2 . Ако природен бројбведнаш го следи бројот a, тогаш бројот a се нарекува непосредно претходен (претходен) бројб.
______________________________________________________________________________________________
Теорема 1. Единицата нема претходен природен број (вистината на теоремата следи веднаш од аксиомата А 1 ).
Теорема 2.Секој природен број А,различен од еден има претходен број б , такви што б " = А.
Дефиницијата за природен број не кажува ништо за природата на елементите на множеството Н.Значи, може да биде се. Стандардниот модел на системот за аксиома Пеано е серија на броеви што се појавија во процесот на историскиот развој на општеството:
1, 2, 3, 4, 5 ,..,
Секој број во оваа серија има своја ознака и име, кои ќе ги сметаме за познати.
Важно е да се напомене дека при дефиницијата за природен број, ниту една од аксиомите не може да се испушти.
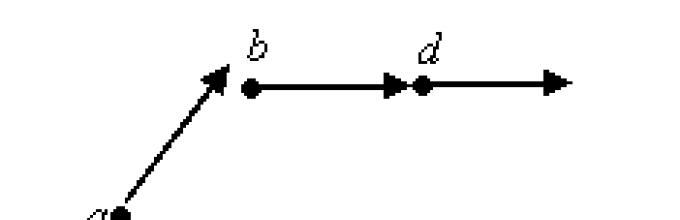
1 а б в г
…
б
Ориз. 16 Ориз. 17
Задача 1.
На сликите, секој елемент е поврзан со стрелка со елементот што следи.
Определете кои од множествата прикажани на сликите 15 и 16 се модели на системот за аксиома Peano.
1. На сл. Слика 16 покажува множество во кое аксиомите 2 и 3 се задоволни, но аксиомата 1 не е задоволена.
Аксиома 4 нема да има смисла, бидејќи не постои елемент во множеството што веднаш не следи друг.
2. На сл. Слика 17 покажува множество во кое аксиомите 1, 2, 3 се задоволни, но аксиомата 4 не е задоволена - множеството точки што лежат на зракот содржи 1, и заедно со секој број го содржи бројот веднаш по него, но го прави тоа. не се совпаѓа со целосните сет точки прикажани на сликата. Заклучок: ниту еден од множествата прикажани на сл. 16 и 17 не можат да се сметаат за модели на системот за аксиома Пеано.
Задача 2.
Да докажеме дека секој природен број е различен од природниот број веднаш по него, т.е. ( X ) X X"
Доказ
Ја користиме аксиомата на индукција - А 4 .
Нека М=(x/x , Х X"}, бидејќи . X М Н.
Доказот се состои од два дела.
Да го докажеме тоа 1 М,тие. 1 1" . Ова произлегува од А 1 .
Да го докажеме тоа X М=> X" М.Нека X Мтие. X X“.Да го докажеме тоа X" М, т.е. X" (Х")". Иаксиоми А 3 треба да X" (X")". Навистина, според А 3 , ако x" = (x)" тогаш x = x", и бидејќи со индукциски предлог x М,потоа x X",Следствено, доаѓаме до контрадикција. Средства, X" (X")" , X" М.
Овде се применува правилото на контрапозиција (PC), широко користено во доказите со контрадикторност.
Така добивме:
М Н (1 М (x M => x" M)) М = N, т.е. изјава x x" е точно за секој природен број.
Контролни прашања
Која е суштината на конструкцијата на аксиоматската теорија?
Наведете ги основните поими на курсот за училишна планиметрија. Запомнете го аксиомскиот систем на овој курс. Својствата на кои концепти се опишани во нив?
Формулирајте и запишете ги аксиомите на Пеано во симболична форма. "
Формулирајте аксиоматска дефиниција за природен број.
Продолжи со дефиницијата за природен број: „Природен број е елемент на множество Н,... » .
Наведете примери од учебниците по математика за основните одделенија во кои:
а) нов (за студенти) број делува како продолжение на добиениот сегмент од природната серија;
б) се утврди дека по секој природен број веднаш следи само уште еден природен број.
Вежби
285. Елементите на множеството се групи цртички (I, II, III, IIII,...). Дали овој сет ги задоволува аксиомите на Пеано? Како што е дефинирано овде, врската „директно следење“ е дефинирана овде. Размислете за истите прашања за множеството (0, 00, 000, 0000,...).



Ориз. 17
286. На слика 17 а) секој елемент е поврзан со стрелка со елементот што следи по него. Може ли множеството да се смета за модел на системот за аксиома Пеано? Истите прашања за множествата на сликите 17 б), в), г).
287. Дали множеството броеви (1, 2, 3) ги задоволува аксиомите на Пеано П, ...),ако релацијата со низа е дефинирана во неа вака:
1 3 5 7….
2 4 6 8….
288. Наведете примери за задачи од учебниците по математика за основните одделенија, во кои правилноста на извршувањето на задачите се објаснува со аксиомите на Пеано.
ОЗО МАТЕМАТИКА 1 година 2 семестар
Пример 1:Да го оправдаме изборот на акција при решавање на проблемот: „Купивме 4 пакувања обоена хартија и 3 пакувања повеќе бела хартија. Колку пакувања бела хартија купивте?
Решение.Проблемот се занимава со две групи. Нека A е збир од пакувања обоена хартија, B е збир на пакувања бела хартија. По услов е познат бројот на пакувања обоена хартија, т.е. n(A)=4 и треба да се најде големината на множеството B. Дополнително, според условите на проблемот, во множеството Б можеме да избереме подмножество C, чиј број е 3, т.е. n(C)=3. Ајде да го направиме ова, на пример, како што е прикажано на сл. 1.
Слика 1
Тогаш разликата B \ C = B 1 ќе биде еднаква на множеството A, т.е. n(B 1) = n(A).
Така, множеството B е заедница на множествата B 1 и C, каде што B 1 C=Æ.
Проблемот се сведува на определување на големината на спојот на две дисјунктирани множества и се решава со собирање: n(B) = n(B 1 C) = n(B 1) + n(C); n(B) = 4+3 = 7.
Пример 2:Користејќи го концептот број како мерка за големина, ќе го оправдаме изборот на дејство при решавање на проблемот: „За здолништето се користеа 3 метри ткаенина, а за блузата 2 метри. Колку метри ткаенина влезе во целото одело?
Решение:Проблемот се занимава со количина - должина, која се мери со помош на единица од 1 метар, бидејќи должината е континуирана, потоа ќе го објасниме изборот на дејство при решавање на проблемот со помош на отсечки (сл. 2).
Нека e=1m, отсечката a ја покажува должината на ткаенината што се користи за здолништето, a=3e. Сегментот b ја покажува должината на ткаенината што се користи за блузата, b = 2e. Бидејќи Во проблемот треба да ја дознаете количината на целата употребена ткаенина, тогаш сегментот c ќе ја означи количината на целата употребена ткаенина: c = a + b.
 Слика 2 Слика 2 | a=3e b=2e m e (c)= m e (a)+m e (c) m e (c) = 2+3 m e (c) = 5 Одговор: 5 m. |
Пример 3:Користејќи го концептот број како мерка за големина, ќе го оправдаме изборот на дејство при решавање на проблемот: „Во првата кутија имаше 12 кг колачиња, а во втората имаше 3 кг помалку. Колку килограми колачиња имало во втората кутија?
Решение:Проблемот се занимава со количината маса, чија единица мерење е 1 килограм, e = 1 kg, бидејќи количина, масата е континуирана, потоа ќе го објасниме изборот на дејство при решавање на проблемот со помош на отсечки (сл. 3).
Нека e = 1kg, сегментот a покажува колку килограми колачиња имало во првата кутија, a = 12e.
Сегментот b покажува колку килограми колачиња имало во втората кутија помалку отколку во првата, b = 3e.
Одделот c покажува колку килограми колачиња имало во втората кутија, m e (c) - ? Познато е дека втората кутија содржи 3 кг колачиња помалку од првата, т.е. исто, но 3 помалку.
| Нека d=a, потоа c = d – b. a = 12e, што значи d = 12e. m e (c) = m e (d)-m e (c) m e (c) = 12-3 m e (c) = 9 |  Слика 3 Слика 3
|
Одговор: Во втората кутија имаше 9 килограми колачиња.