А)Решете ја равенката 2(\sin x-\cos x)=tgx-1.
б) \лево[ \frac(3\pi )2;\,3\pi \десно].
Прикажи решениеРешение
А)Отворајќи ги заградите и поместувајќи ги сите членови на левата страна, ја добиваме равенката 1+2 \sin x-2 \cos x-tg x=0. Имајќи предвид дека \cos x \neq 0, терминот 2 \sin x може да се замени со 2 tan x \cos x, ја добиваме равенката 1+2 tg x \cos x-2 \cos x-tg x=0,кој со групирање може да се сведе на формата (1-tg x)(1-2 \cos x)=0.
1) 1-tg x=0, тен x=1, x=\frac\pi 4+\pi n, n \in \mathbb Z;
2) 1-2 \cos x=0, \cos x=\frac12, x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z.
б)Со користење на круг со бројизберете ги корените кои припаѓаат на интервалот \лево[ \frac(3\pi )2;\, 3\pi \десно].
x_1=\frac\pi 4+2\pi =\frac(9\pi)4,
x_2=\frac\pi 3+2\pi =\frac(7\pi)3,
x_3=-\frac\pi 3+2\pi =\frac(5\pi )3.
Одговори
А) \frac\pi 4+\pi n, \pm\frac\pi 3+2\pi n, n \in \mathbb Z;
б) \frac(5\pi)3, \frac(7\pi)3, \frac(9\pi)4.
Состојба
А)Решете ја равенката (2\sin ^24x-3\cos 4x)\cdot \sqrt (tgx)=0.
б)Наведете ги корените на оваа равенка кои припаѓаат на интервалот \left(0;\,\frac(3\pi )2\десно] ;
Прикажи решениеРешение
А)ОДЗ: \begin(случаи) tgx\geqslant 0\\x\neq \frac\pi 2+\pi k,k \in \mathbb Z. \end(случаи)
Оригиналната равенка на ODZ е еквивалентна на множество равенки
\left[\!\!\begin(array)(l) 2 \sin ^2 4x-3 \cos 4x=0,\\tg x=0. \крај (низа)\десно.
Да ја решиме првата равенка. За да го направите ова, ќе направиме замена \cos 4x=t, t \in [-1; 1].Потоа \sin^24x=1-t^2. Добиваме:
2(1-t^2)-3t=0,
2t^2+3t-2=0,
t_1=\frac12, t_2=-2, t_2\не [-1; 1].
\cos 4x=\frac12,
4x=\pm\frac\pi 3+2\pi n,
x=\pm \frac\pi (12)+\frac(\pi n)2, n \in \mathbb Z.
Да ја решиме втората равенка.
tg x=0,\, x=\pi k, k \in \mathbb Z.
Со помош единица кругДа најдеме решенија кои ги задоволуваат ОДЗ.

Знакот „+“ ги означува 1-та и 3-та четвртина, во кои tg x>0.
Добиваме: x=\pi k, k \in \mathbb Z; x=\frac\pi (12)+\pi n, n \in \mathbb Z; x=\frac(5\pi )(12)+\pi m, m \in \mathbb Z.
б)Ајде да ги најдеме корените кои припаѓаат на интервалот \left(0;\,\frac(3\pi)2\десно].
.png)
x=\frac\pi (12), x=\frac(5\pi)(12); x=\pi ; x=\frac(13\pi)(12); x=\frac(17\pi)(12).
Одговори
А) \pi k, k \in \mathbb Z; \frac\pi (12)+\pi n, n \in \mathbb Z; \frac(5\pi )(12)+\pi m, m \in \mathbb Z.
б) \pi; \frac\pi (12); \frac(5\pi)(12); \frac(13\pi)(12); \frac(17\pi)(12).
Извор: „Математика. Подготовка за Единствен државен испит 2017 година. Ниво на профил" Ед. Ф. Ф. Лисенко, С. Ју. Кулабухова.
Состојба
А)Реши ја равенката: \cos ^2x+\cos ^2\frac\pi 6=\cos ^22x+\sin ^2\frac\pi 3;
б)Наведете ги сите корени кои припаѓаат на интервалот \left(\frac(7\pi)2;\,\frac(9\pi)2\десно].
Прикажи решениеРешение
А)Бидејќи \sin \frac\pi 3=\cos \frac\pi 6,Тоа \sin ^2\frac\pi 3=\cos ^2\frac\pi 6,Средства, дадена равенкае еквивалентна на равенката \cos^2x=\cos ^22x, што, пак, е еквивалентно на равенката \cos^2x-\cos ^2 2x=0.
Но \cos ^2x-\cos ^22x= (\cos x-\cos 2x)\cdot (\cos x+\cos 2x)И
\cos 2x=2 \cos ^2 x-1, па равенката станува
(\cos x-(2 \cos ^2 x-1))\,\cdot(\cos x+(2 \cos ^2 x-1))=0,
(2 \cos ^2 x-\cos x-1)\,\cdot (2 \cos ^2 x+\cos x-1)=0.
Тогаш или 2 \cos ^2 x-\cos x-1=0, или 2 \cos ^2 x+\cos x-1=0.
Решавање на првата равенка како квадратна равенкаво однос на \cos x, добиваме:
(\cos x)_(1,2)=\frac(1\pm\sqrt 9)4=\frac(1\pm3)4.Затоа или \cos x=1 или \cos x=-\frac12.Ако \cos x=1, тогаш x=2k\pi , k \in \mathbb Z. Ако \cos x=-\frac12,Тоа x=\pm \frac(2\pi)3+2s\pi, s \in \mathbb Z.
Слично, решавајќи ја втората равенка, добиваме или \cos x=-1 или \cos x=\frac12.Ако \cos x=-1, тогаш корените x=\pi +2m\pi , m \in \mathbb Z.Ако \cos x=\frac12,Тоа x=\pm \frac\pi 3+2n\pi , n \in \mathbb Z.
Ајде да ги комбинираме добиените решенија:
x=m\pi , m \in \mathbb Z; x=\pm \frac\pi 3 +s\pi , s \in \mathbb Z.
б)Ајде да ги избереме корените што спаѓаат во даден интервал користејќи круг со број.

Добиваме: x_1 =\frac(11\pi)3, x_2=4\pi, x_3 =\frac(13\pi)3.
Одговори
А) m\pi, m\in \mathbb Z; \pm \frac\pi 3 +s\pi , s \in \mathbb Z;
б) \frac(11\pi)3, 4\pi, \frac(13\pi)3.
Извор: „Математика. Подготовка за Единствен државен испит 2017 година. Ниво на профил." Ед. Ф. Ф. Лисенко, С. Ју. Кулабухова.
Состојба
А)Решете ја равенката 10\cos ^2\frac x2=\frac(11+5ctg\лево(\dfrac(3\pi)2-x\десно) )(1+tgx).
б)Наведете ги корените на оваа равенка кои припаѓаат на интервалот \left(-2\pi ; -\frac(3\pi)2\десно).
Прикажи решениеРешение
А) 1. Според формулата за намалување, ctg\left(\frac(3\pi)2-x\десно) =tgx.Доменот на дефиниција на равенката ќе биде такви вредности на x такви што \cos x \neq 0 и tan x \neq -1. Ајде да ја трансформираме равенката користејќи ја косинусната формула со двоен агол 2 \cos ^2 \frac x2=1+\cos x.Ја добиваме равенката: 5(1+\cos x) =\frac(11+5tgx)(1+tgx).
забележи, тоа \frac(11+5tgx)(1+tgx)= \frac(5(1+tgx)+6)(1+tgx)= 5+\frac(6)(1+tgx),па равенката станува: 5+5 \cos x=5 +\frac(6)(1+tgx).Од тука \cos x =\frac(\dfrac65)(1+tgx), \cos x+\sin x =\frac65.
2. Трансформирајте \sin x+\cos x користејќи ја формулата за редукција и формулата за збир на косинуси: \sin x=\cos \left(\frac\pi 2-x\десно), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\десно)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\десно)= \sqrt 2\cos \left(x-\frac\pi 4\десно) = \frac65.
Од тука \cos \left(x-\frac\pi 4\десно) =\frac(3\sqrt 2)5.Средства, x-\frac\pi 4= arc\cos \frac(3\sqrt 2)5+2\pi k, k \in \mathbb Z,
или x-\frac\pi 4= -arc\cos \frac(3\sqrt 2)5+2\pi t, t \in \mathbb Z.
Затоа x=\frac\pi 4+arc\cos \frac(3\sqrt 2)5+2\pi k,k \in \mathbb Z,
или x =\frac\pi 4-arc\cos \frac(3\sqrt 2)5+2\pi t,t \in \mathbb Z.
Пронајдените вредности на x припаѓаат на доменот на дефиниција.
б)Прво да откриеме каде корените на равенката паѓаат при k=0 и t=0. Тоа ќе бидат бројки соодветно a=\frac\pi 4+arccos \frac(3\sqrt 2)5И b=\frac\pi 4-arccos \frac(3\sqrt 2)5.
1. Да ја докажеме помошната неравенка:
\frac(\sqrt 2)(2)<\frac{3\sqrt 2}2<1.
Навистина, \frac(\sqrt 2)(2)=\frac(5\sqrt 2)(10)<\frac{6\sqrt2}{10}=\frac{3\sqrt2}{5}.
Забележете го и тоа \left(\frac(3\sqrt 2)5\десно) ^2=\frac(18)(25)<1^2=1, Средства \frac(3\sqrt 2)5<1.
2. Од нееднаквости (1) Според косинусното својство на лакот добиваме:
лак 1 0 Од тука \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,
0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,
0 Исто така, -\frac\pi 4 0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5<
0 За k=-1 и t=-1 ги добиваме корените на равенката a-2\pi и b-2\pi. \Bigg(a-2\pi =-\frac74\pi +arccos \frac(3\sqrt 2)5,\, b-2\pi =-\frac74\pi -arccos \frac(3\sqrt 2)5\Bigg).При што -2\pi 2\pi За другите вредности на k и t, корените на равенката не припаѓаат на дадениот интервал. Навистина, ако k\geqslant 1 и t\geqslant 1, тогаш корените се поголеми од 2\pi. Ако k\leqslant -2 и t\leqslant -2, тогаш корените се помали -\frac(7\pi)2. А) \frac\pi4\pm arccos\frac(3\sqrt2)5+2\pi k, k\in\mathbb Z; б) -\frac(7\pi)4\pm arccos\frac(3\sqrt2)5. Извор: „Математика. Подготовка за Единствен државен испит 2017 година. Ниво на профил." Ед. Ф. Ф. Лисенко, С. Ју. Кулабухова. А)Решете ја равенката \sin \left(\frac\pi 2+x\десно) =\sin (-2x). б)Најди ги сите корени на оваа равенка што припаѓаат на интервалот ; А)Ајде да ја трансформираме равенката: \cos x =-\sin 2x, \cos x+2 \sin x \cos x=0, \cos x(1+2 \sin x)=0, \cos x=0, x =\frac\pi 2+\pi n, n\in \mathbb Z; 1+2 \sin x=0, \sin x=-\frac12, x=(-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z. б)Корените кои припаѓаат на отсечката ги наоѓаме користејќи го единечниот круг. Посочениот интервал содржи еден број \frac\pi 2. А) \frac\pi 2+\pi n, n \in \mathbb Z; (-1)^(k+1)\cdot \frac\pi 6+\pi k, k \in \mathbb Z; б) \frac\pi 2. Извор: „Математика. Подготовка за Единствен државен испит 2017 година. Ниво на профил." Ед. Ф. Ф. Лисенко, С. Ју. Кулабухова. Средства, \sin x \neq 1. Поделете ги двете страни на равенката со фактор (\sin x-1),различен од нула. Ја добиваме равенката \frac 1(1+\cos 2x)=\frac 1(1+\cos (\pi +x)),или равенка 1+\cos 2x=1+\cos (\pi +x).Применувајќи ја формулата за намалување на левата страна и формулата за намалување на десната страна, ја добиваме равенката 2 \cos ^2 x=1-\cos x.Оваа равенка е со замена \cos x=t,Каде -1 \leqslant t \leqslant 1намалете го на квадрат: 2t^2+t-1=0,чии корени t_1=-1И t_2=\frac12.Враќајќи се на променливата x, добиваме \cos x = \frac12или \cos x=-1,каде x=\frac \pi 3+2\pi m, m \in \mathbb Z, x=-\frac \pi 3+2\pi n, n \in \mathbb Z, x=\pi +2\pi k, k \in \mathbb Z. б)Ајде да ги решиме нееднаквостите 1) -\frac(3\pi)2 \leqslant \frac(\pi)3+2\pi m \leqslant -\frac \pi 2, 2) -\frac(3\pi )2 \leqslant -\frac \pi 3+2\pi n \leqslant -\frac \pi (2,) 3) -\frac(3\pi )2 \leqslant \pi+2\pi k \leqslant -\frac \pi 2, 1)
-\frac(3\pi )2 \leqslant \frac(\pi)3+2\pi m \leqslant -\frac \pi 2, -\frac32\leqslant \frac13+2m \leqslant -\frac12 -\frac(11)6 \leqslant 2m\leqslant -\frac56, -\frac(11)(12) \leqslant m \leqslant -\frac5(12). \лево [-\frac(11)(12);-\frac5(12)\десно]. 2)
-\frac (3\pi) 2 \leqslant -\frac(\pi )3+2\pi n \leqslant -\frac(\pi )(2), -\frac32 \leqslant -\frac13 +2n \leqslant -\frac12, -\frac76 \leqslant 2n \leqslant -\frac1(6), -\frac7(12) \leqslant n \leqslant -\frac1(12). Нема цели броеви во опсегот \left[ -\frac7(12) ; -\frac1(12)\десно]. 3)
-\frac(3\pi )2 \leqslant \pi +2\pi k\leqslant -\frac(\pi)2, -\frac32 \leqslant 1+2k\leqslant -\frac12, -\frac52 \leqslant 2k \leqslant -\frac32, -\frac54 \leqslant k \leqslant -\frac34. Оваа неравенка се задоволува со k=-1, потоа x=-\pi. А) \frac \pi 3+2\pi m; -\frac \pi 3+2\pi n; \pi +2\pi k, m, n, k \in \mathbb Z; б) -\pi . Во оваа статија ќе се обидам да објаснам 2 начини избирање корени во тригонометриска равенка: користење неравенки и користење на тригонометрискиот круг. Ајде да преминеме директно на илустративен пример и ќе сфатиме како функционираат работите. А) Решете ја равенката sqrt(2)cos^2x=sin(Pi/2+x) Да ја решиме точката а. Да ја користиме формулата за редукција за синусен sin(Pi/2+x) = cos(x) Sqrt(2)cos^2x = cosx Sqrt(2)cos^2x - cosx = 0 Cosx(sqrt(2)cosx - 1) = 0 X1 = Pi/2 + Пин, n ∈ Z Sqrt(2)cosx - 1 = 0 Cosx = 1/sqrt(2) Cosx = sqrt(2)/2 X2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z X2 = Pi/4 + 2Pin, n ∈ Z Да ја решиме точката б. 1) Избор на корени со помош на неравенки Овде сè е направено едноставно, ние ги заменуваме добиените корени во интервалот што ни е даден [-7Pi/2; -2Pi], пронајдете цели броеви за n. 7Pi/2 помал или еднаков на Pi/2 + Пин помал или еднаков на -2Pi Веднаш делиме сè со Пи 7/2 помало или еднакво на 1/2 + n помало или еднакво на -2 7/2 - 1/2 помала или еднаква на n помала или еднаква на -2 - 1/2 4 помало или еднакво на n помало или еднакво на -5/2 Целиот број n во овој интервал се -4 и -3. Ова значи дека корените кои припаѓаат на овој интервал ќе бидат Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2 На сличен начин правиме уште две неравенки 7Pi/2 помала или еднаква на Pi/4 + 2Pin помала или еднаква на -2Pi Во овој интервал нема цели n 7Pi/2 помала или еднаква на -Pi/4 + 2Pin помала или еднаква на -2Pi Еден цел број n во овој интервал е -1. Ова значи дека избраниот корен на овој интервал е -Pi/4 + 2Pi*(-1) = -9Pi/4. Значи одговорот во точката б: -7Pi/2, -5Pi/2, -9Pi/4 2) Избор на корени со помош на тригонометриски круг За да го користите овој метод, треба да разберете како функционира овој круг. Ќе се обидам да објаснам на едноставен јазик како го разбирам ова. Мислам дека во училиштата, на часовите по алгебра, оваа тема многупати се објаснуваше со паметни зборови од наставникот, во учебниците имаше сложени формулации. Лично, јас го разбирам ова како круг околу кој може да се шета бесконечен број пати, ова се објаснува со фактот дека синусните и косинусните функции се периодични. Ајде да одиме наоколу спротивно од стрелките на часовникот Ајде да одиме околу 2 пати спротивно од стрелките на часовникот Ајде да одиме околу 1 пат во насока на стрелките на часовникот (вредностите ќе бидат негативни) Да се вратиме на нашето прашање, треба да избереме корени во интервалот [-7Pi/2; -2 Pi] За да дојдете до броевите -7Pi/2 и -2Pi треба двапати да го заобиколите кругот спротивно од стрелките на часовникот. За да ги пронајдете корените на равенката на овој интервал, треба да ги процените и замените. Размислете за x = Pi/2 + Пин. Приближно колку треба да биде n за x да биде некаде во овој опсег? Заменуваме, да речеме -2, добиваме Pi/2 - 2Pi = -3Pi/2, очигледно ова не е вклучено во нашиот интервал, па земаме помалку од -3, Pi/2 - 3Pi = -5Pi/2, ова е погоден, ајде да се обидеме повторно -4 , Pi/2 - 4Pi = -7Pi/2, исто така погоден. Расудувајќи слично за Pi/4 + 2Pin и -Pi/4 + 2Pin, наоѓаме друг корен -9Pi/4. Споредба на два методи. Првиот метод (користење нееднаквости) е многу посигурен и многу полесен за разбирање, но ако навистина се зафатите со тригонометрискиот круг и вториот метод на селекција, тогаш изборот на корените ќе биде многу побрз, можете да заштедите околу 15 минути на испитот . а) Решете ја равенката: . б) Најдете ги сите корени на оваа равенка што припаѓаат на отсечката. Оваа лекција дискутира за пример за решавање на тригонометриска равенка, која може да се користи како пример за решавање проблеми од типот C1 при подготовка за обединет државен испит по математика. Пред сè, се одредува опсегот на функцијата - сите валидни вредности на аргументот. Потоа, за време на растворот, тригонометриската синусна функција се претвора во косинус со помош на формулата за редукција. Следно, сите поими од равенката се пренесуваат на неговата лева страна, каде што заедничкиот фактор е изваден од заградите. Секој фактор е еднаков на нула, што ни овозможува да ги одредиме корените на равенката. Потоа, користејќи го методот на вртења, се одредуваат корените кои припаѓаат на даден сегмент. За да го направите ова, на конструираниот единичен круг, се означува пресврт од левата граница на даден сегмент надесно. Следно, пронајдените корени на единечниот круг се поврзани со отсечки со неговиот центар и се одредуваат точките во кои овие отсечки го пресекуваат свиокот. Овие пресечни точки се посакуваниот одговор на вториот дел од проблемот. Можете да нарачате детално решение за вашиот проблем!!! Еднаквоста што содржи непозната под знакот на тригонометриска функција („sin x, cos x, tan x“ или „ctg x“) се нарекува тригонометриска равенка, а нивните формули ќе ги разгледаме понатаму. Наједноставните равенки се `sin x=a, cos x=a, tg x=a, ctg x=a`, каде што `x` е аголот што треба да се најде, `a` е кој било број. Дозволете ни да ги запишеме коренските формули за секоја од нив. 1. Равенка `sin x=a`. За `|a|>1` нема решенија. Кога `|а| \leq 1` има бесконечен број решенија. Формула на коренот: `x=(-1)^n arcsin a + \pi n, n \in Z` 2. Равенка `cos x=a` За `|a|>1` - како и во случајот со синус, тој нема решенија меѓу реалните броеви. Кога `|а| \leq 1` има бесконечен број решенија. Формула на коренот: `x=\pm arccos a + 2\pi n, n \in Z` Специјални случаи за синус и косинус во графикони. 3. Равенка `tg x=a` Има бесконечен број решенија за која било вредност на `a`. Формула на коренот: `x=arctg a + \pi n, n \in Z` 4. Равенка `ctg x=a` Исто така, има бесконечен број решенија за сите вредности на `a`. Формула на коренот: `x=arcctg a + \pi n, n \in Z` За синус: Решавањето на која било тригонометриска равенка се состои од две фази: Ајде да ги разгледаме главните методи на решение користејќи примери. Овој метод вклучува замена на променлива и нејзина замена во еднаквост. Пример. Решете ја равенката: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0` `2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`, направи замена: `cos(x+\frac \pi 6)=y`, потоа `2y^2-3y+1=0`, ги наоѓаме корените: `y_1=1, y_2=1/2`, од кои следуваат два случаи: 1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`. 2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`. Одговор: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`. Пример. Решете ја равенката: `sin x+cos x=1`. Решение. Да ги преместиме сите членови на еднаквоста налево: `sin x+cos x-1=0`. Со помош на , ја трансформираме и факторизираме левата страна: `sin x — 2sin^2 x/2=0`, `2sin x/2 cos x/2-2sin^2 x/2=0`, `2sin x/2 (cos x/2-sin x/2)=0`, Одговор: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`. Прво, треба да ја намалите оваа тригонометриска равенка на една од двете форми: `a sin x+b cos x=0` (хомогена равенка од прв степен) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (хомогена равенка од втор степен). Потоа поделете ги двата дела со `cos x \ne 0` - за првиот случај, и со `cos^2 x \ne 0` - за вториот. Добиваме равенки за `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, кои треба да се решат со познати методи. Пример. Решете ја равенката: `2 sin^2 x+sin x cos x - cos^2 x=1`. Решение. Ајде да ја напишеме десната страна како `1=sin^2 x+cos^2 x`: `2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`, `2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0` `sin^2 x+sin x cos x — 2 cos^2 x=0`. Ова е хомогена тригонометриска равенка од втор степен, ја делиме нејзината лева и десна страна со `cos^2 x \ne 0`, добиваме: `\ frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0` `tg^2 x+tg x — 2=0`. Да ја воведеме замената `tg x=t`, што резултира со `t^2 + t - 2=0`. Корените на оваа равенка се `t_1=-2` и `t_2=1`. Потоа: Одговори. `x_1=arctg (-2)+\pi n`, `n \во Z`, `x_2=\pi/4+\pi n`, `n \во Z`. Пример. Решете ја равенката: `11 sin x - 2 cos x = 10`. Решение. Да ги примениме формулите за двоен агол, што резултира со: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2` `4 tg^2 x/2 — 11 tg x/2 +6=0` Применувајќи го алгебарскиот метод опишан погоре, добиваме: Одговори. `x_1=2 arctg 2+2\pi n, n \во Z`, `x_2=arctg 3/4+2\pi n`, `n \во Z`. Во тригонометриската равенка „a sin x + b cos x =c“, каде што a,b,c се коефициенти и x е променлива, поделете ги двете страни со `sqrt (a^2+b^2)`: `\ frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 ) +b^2))`. Коефициентите од левата страна имаат својства на синус и косинус, имено збирот на нивните квадрати е еднаков на 1, а нивните модули не се поголеми од 1. Да ги означиме на следниов начин: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, тогаш: `cos \varphi sin x + sin \varphi cos x =C`. Да го разгледаме подетално следниот пример: Пример. Решете ја равенката: `3 sin x+4 cos x=2`. Решение. Поделете ги двете страни на еднаквоста со `sqrt (3^2+4^2)`, добиваме: `\ frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))` `3/5 грев x+4/5 cos x=2/5`. Да означиме `3/5 = cos \varphi` , `4/5=sin \varphi`. Бидејќи `sin \varphi>0`, `cos \varphi>0`, тогаш земаме `\varphi=arcsin 4/5` како помошен агол. Потоа ја пишуваме нашата еднаквост во форма: `cos \varphi sin x+sin \varphi cos x=2/5` Применувајќи ја формулата за збир на агли за синус, ја запишуваме нашата еднаквост во следнава форма: `sin (x+\varphi)=2/5`, `x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`, `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`. Одговори. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`. Станува збор за равенки со дропки чии броител и именители содржат тригонометриски функции. Пример. Решете ја равенката. `\frac (sin x)(1+cos x)=1-cos x`. Решение. Помножете ја и поделете ја десната страна на еднаквоста со `(1+cos x)`. Како резултат добиваме: `\ frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)` `\ frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)` `\ frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)` `\ frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0` `\frac (sin x-sin^2 x)(1+cos x)=0` Имајќи предвид дека именителот не може да биде еднаков на нула, добиваме `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`. Да го изедначиме броителот на дропката со нула: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Потоа `sin x=0` или `1-sin x=0`. Имајќи предвид дека ` x \ne \pi+2\pi n, n \in Z`, решенијата се `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n` , `n \во Z`. Одговори. `x=2\pi n`, `n \во Z`, `x=\pi /2+2\pi n`, `n \во Z`. Тригонометријата, а особено тригонометриските равенки, се користат во речиси сите области на геометријата, физиката и инженерството. Учењето започнува во 10-то одделение, секогаш има задачи за Единствениот државен испит, затоа обидете се да ги запомните сите формули на тригонометриски равенки - тие дефинитивно ќе ви бидат корисни! Сепак, дури и не треба да ги меморирате, главната работа е да ја разберете суштината и да можете да ја изведете. Не е толку тешко како што изгледа. Уверете се сами гледајќи го видеото. Целта на лекцијата: А) зајакнување на способноста за решавање едноставни тригонометриски равенки; б) научете како да изберете корени на тригонометриски равенки од даден интервал а) Проверка на домашна задача: на часот добива напредна домашна задача - реши равенка и најде начин да избере корени од даден интервал. 1) кос x= -0,5, каде xI [- ]. Одговор:. 2) грев x= , каде xI . Одговор: ; . 3) co 2 x= -, каде xI. Одговор: Учениците го запишуваат решението на табла, некои со графикон, други со методот на селекција. Во ова време класа работи усно. Најдете го значењето на изразот: а) tg – грев + cos + грев. Одговор: 1. б) 2 arccos 0 + 3 arccos 1. Одговор:? в) arcsin + arcsin. Одговор:. г) 5 arctg (-) – arccos (-). Одговор: -. – Ајде да си ги провериме домашните задачи, да ги отвориме тетратките со домашните задачи. Некои од вас го нашле решението користејќи го методот на селекција, а некои користејќи го графикот. 2. Заклучок за начините на решавање на овие задачи и изјава за проблемот, односно комуникација на темата и целта на часот. – а) Тешко е да се реши со користење на селекција ако е даден голем интервал. – б) Графичкиот метод не дава точни резултати, бара проверка и одзема многу време. – Затоа, мора да има барем уште еден метод, најуниверзален - да се обидеме да го најдеме. Па, што ќе правиме на час денес? (Научете да ги избирате корените на тригонометриската равенка на даден интервал.) – Пример 1. (Ученикот оди на табла) cos x= -0,5, каде што xI [- ]. Прашање: Што го одредува одговорот на оваа задача? (Од општото решение на равенката. Да го запишеме решението во општа форма). Решението се пишува на табла x = + 2?k, каде k R. – Да го напишеме ова решение во форма на множество: – Според вас, во која нотација на решението е погодно да се изберат корени на интервалот? (од вториот запис). Но, ова е повторно метод на селекција. Што треба да знаеме за да го добиеме вистинскиот одговор? (Треба да ги знаете вредностите на k). (Ајде да создадеме математички модел за да го најдеме k). бидејќи kI Z, тогаш k = 0, оттука X= = Од оваа неравенка е јасно дека нема целобројни вредности на k. Заклучок:За да изберете корени од даден интервал при решавање на тригонометриска равенка, потребно е: Решете ги примерите бр. 2 и бр. 3 од домашната задача користејќи го добиениот алгоритам. На таблата истовремено работат двајца ученици, по што следи проверка на работата.Одговори
Состојба
Решение

Одговори
Состојба
не е вклучен во ДЗ. Одговори
б) Најдете ги сите корени на оваа равенка кои припаѓаат на интервалот [-7Pi/2; -2 Pi]
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
-15/8 помала или еднаква на n помала или еднаква на -9/8
-13/8 помала или еднаква на n помала или еднаква на -7/8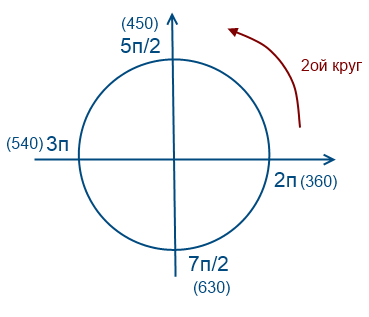


Решението на проблемот





Формули за корените на тригонометриските равенки во табелата
 За косинус:
За косинус:  За тангента и котангента:
За тангента и котангента:  Формули за решавање равенки кои содржат инверзни тригонометриски функции:
Формули за решавање равенки кои содржат инверзни тригонометриски функции:
Методи за решавање на тригонометриски равенки
Алгебарски метод.
Факторизација.
Намалување на хомогена равенка
Преместување на половина агол
Воведување на помошен агол
Дробни рационални тригонометриски равенки
За време на часовите.
1. Ажурирање на знаењето.

3. Консолидација.








