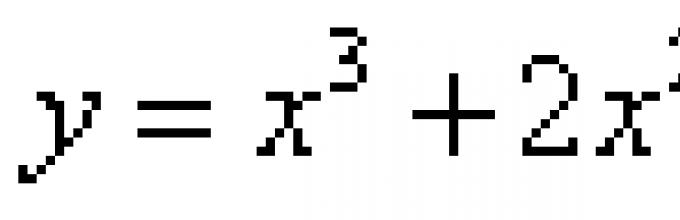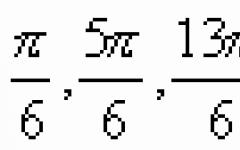Тангента е права линија , кој го допира графикот на функцијата во една точка и сите точки се на најкратко растојание од графикот на функцијата. Според тоа, тангентата поминува тангента на графикот на функцијата под одреден агол и неколку тангенти под различни агли не можат да поминат низ точката на тангенција. Тангентни равенки и нормални равенки на графикот на функцијата се конструирани со помош на изводот.
Тангентната равенка е изведена од линиската равенка .
Да ја изведеме равенката на тангентата, а потоа равенката на нормалата на графикот на функцијата.
y = kx + б .
Во него к - наклон.
Од тука го добиваме следниот запис:
y - y 0 = к(x - x 0 ) .
Изводна вредност ѓ "(x 0 ) функции y = ѓ(x) во точката x0 еднаков на наклонот к= tg φ тангента на графикот на функција нацртана низ точка М0 (x 0 , y 0 ) , Каде y0 = ѓ(x 0 ) . Ова е геометриско значењедериват .
Така, можеме да замениме кна ѓ "(x 0 ) и добијте го следново равенка на тангента на графикот на функција :
y - y 0 = ѓ "(x 0 )(x - x 0 ) .
Во проблемите што вклучуваат составување на равенката на тангента на графикот на функцијата (и ќе продолжиме на нив наскоро), потребно е да се намали равенката добиена од горната формула на равенка на права линија во општа форма. За да го направите ова, треба да ги преместите сите букви и бројки на левата страна од равенката и да оставите нула на десната страна.
Сега за нормалната равенка. Нормално - ова е права линија што минува низ точката на тангенција на графикот на функцијата нормална на тангентата. Нормална равенка :
(x - x 0 ) + ѓ "(x 0 )(y - y 0 ) = 0
За да се загреете, од вас се бара сами да го решите првиот пример, а потоа да го погледнете решението. Има секоја причина да се надеваме дека оваа задача нема да биде „ладен туш“ за нашите читатели.
Пример 0.Направете тангентна равенка и нормална равенка за графикот на функцијата во точка М (1, 1) .
Пример 1.Напишете тангентна равенка и нормална равенка за графикот на функцијата ![]() , ако апсцисата е тангента .
, ако апсцисата е тангента .
Да го најдеме изводот на функцијата:
Сега имаме сè што треба да се замени во записот даден во теоретската помош за да се добие тангентната равенка. Добиваме
![]()
Во овој пример, имавме среќа: коефициентот на наклон се покажа нула, така што немаше потреба одделно да ја доведеме равенката во нејзината општа форма. Сега можеме да ја создадеме нормалната равенка:
![]()
На сликата подолу: график на функција во бордо боја, тангента зелена, портокалова нормална.

Следниот пример исто така не е комплициран: функцијата, како и во претходната, е исто така полином, но наклонот нема да биде еднаков на нула, па ќе се додаде уште еден чекор - доведување на равенката во општа форма.
Пример 2.
Решение. Да ја најдеме ординатата на тангентата точка:
Да го најдеме изводот на функцијата:
![]() .
.
Да ја најдеме вредноста на изводот на точката на тангенција, односно наклонот на тангентата:
Сите добиени податоци ги заменуваме во „празна формула“ и ја добиваме тангентата равенка:
![]()
Ја доведуваме равенката во нејзината општа форма (ги собираме сите букви и броеви освен нула на левата страна, а оставаме нула на десната):
Ја составуваме нормалната равенка:

Пример 3.Напиши ја равенката на тангентата и равенката на нормалата на графикот на функцијата ако апсцисата е точка на тангенција.
Решение. Да ја најдеме ординатата на тангентата точка:
Да го најдеме изводот на функцијата:
![]() .
.
Да ја најдеме вредноста на изводот на точката на тангенција, односно наклонот на тангентата:
![]() .
.
Ја наоѓаме тангентата равенка:

Пред да ја доведете равенката во нејзината општа форма, треба малку да ја „чешлате“: помножете член по член со 4. Ние го правиме ова и ја доведуваме равенката во нејзината општа форма:
Ја составуваме нормалната равенка:

Пример 4.Напиши ја равенката на тангентата и равенката на нормалата на графикот на функцијата ако апсцисата е точка на тангенција.
Решение. Да ја најдеме ординатата на тангентата точка:
![]() .
.
Да го најдеме изводот на функцијата:
Да ја најдеме вредноста на изводот на точката на тангенција, односно наклонот на тангентата:
![]() .
.
Ја добиваме тангентата равенка:
Ја доведуваме равенката во нејзината општа форма:
Ја составуваме нормалната равенка:
![]()
Честа грешка при пишување тангентни и нормални равенки е да не се забележи дека функцијата дадена во примерот е сложена и да се пресмета нејзиниот извод како извод на едноставна функција. Следниве примери се веќе од сложени функции(соодветната лекција ќе се отвори во нов прозорец).
Пример 5.Напиши ја равенката на тангентата и равенката на нормалата на графикот на функцијата ако апсцисата е точка на тангенција.
Решение. Да ја најдеме ординатата на тангентата точка:
Внимание! Оваа функција е сложена, бидејќи аргументот тангента (2 x) е самата функција. Затоа, го наоѓаме изводот на функцијата како извод на сложена функција.
Дефиниција: нормалата на кривата y = ¦(x) во точката M 0 е права линија што минува низ точката M 0 и е нормална на тангентата во точката M 0 на оваа крива.
Да ја напишеме равенката на тангентата и нормалната, знаејќи ја равенката на кривата и координатите на точката M 0. Тангентата има аголен коефициент k = t g = ¦, (x 0). Од аналитичката геометрија се знае дека права линија има равенка y-y 0 = k(x – x 0).
Според тоа, тангентната равенка е: y - y 0 = ¦, (x 0)(x – x 0); (1)
Аголниот коефициент на нормалата е Kn = (бидејќи се нормални), но тогаш равенката на нормалата е:
y-y 0 =(-1/ ¦, (x 0) (x – x 0); (2)
Ако изводот не постои во точка, тогаш тангента не постои во оваа точка.
На пример, функцијата ¦(x)=|x| во точката x=0 нема извод.
lim D x ®0 (D y/ D x) = lim D x ®0 (| D x|/ D x) =
Еднострани граници постојат, но lim D x ®0 (D y/ D x) не постои
Тангента исто така.
Оваа точка се нарекува аголна точка на графикот.
§4. Врска помеѓу континуитет и диференцијабилност на функција.
Валидна е следната теорема за диференцијабилна функција.
Теорема: ако функцијата y = ¦(x) има конечен извод во точката x 0, тогаш функцијата е континуирана во оваа точка.
Доказ:
Бидејќи во точката x 0 има извод ¦, (x 0), т.е. има граница
lim D x ®0 (D y/ D x)= ¦, (x 0), потоа D y/ D x= ¦, (x 0)+, каде
B.m.v., во зависност од D x. Кога D x®0, ®0, бидејќи = (D y/ D x) - ¦, (x 0) ®0 на D x®0
Оттука имаме: D y= ¦, (x 0) D x + D x.
Но тогаш
Бесконечно мало зголемување во аргументот одговара на бесконечно мало зголемување во функцијата, затоа ¦(x) е континуирано во точката x 0 .
Важно е да се разбере тоа конверзна теоремане е вистина!
Не секој континуирана функцијае диференцијабилна.
Значи, ¦(x) =|x| е континуирано во точката x 0 =0, графикот е солидна линија, но ¦, (0) не постои.
§5. Деривати на функции на константа, синус, косинус и моќност.
1. y= ¦(x) =c; y, = (c), = 0; (1)
Доказ:
а) во која било точка x ¦(x) = c
б) дајте му на x инкрементот D x, x + D x, вредноста на функцијата ¦ (x + D x) = c;
в) ¦ (x + D x)- ¦ (x)= с- с= 0;
г) D y/ D x = 0/ D x = 0
д) lim D x ®0 (D y/ D x) = lim D x ®0 0 = 0
2. y= грев x; y, = (грев x), = cos x; (2)
Доказ:
а) во која било точка x ¦(x) = sin x;
б) дајте му на x зголемувањето на D x, x + D x, вредноста на функцијата
Тема : Поими на тангента и нормално.
Тангентни и нормални равенки.
Цели:
Тема: да ги запознае учениците со поимите: тангента и нормално на крива; консолидирајте ги овие концепти при решавање на проблеми за составување тангентни и нормални равенки; дознајте какви својства имаат аголните коефициенти на тангентата и нормалата.
Комуникативно: аргументирајте ја вашата гледна точка, расправајте се и бранете ја вашата позиција на непријателски начин за противниците; да можат да се слушаат и слушаат.
Когнитивни : воспоставување причинско-последични односи; го изразуваат значењето на ситуацијата користејќи различни средства (цртежи, симболи, дијаграми, знаци).
Регулаторни: прифати когнитивна цел, зачувајте го при извршувањето едукативни активности, го регулираат целиот процес на нивно спроведување и јасно ги исполнуваат барањата на когнитивната задача.
Лични: формирање на когнитивен интерес за учење нови работи, мотивација за самостојни и колективни истражувачки активности.
Напредокот на лекцијата:
1. Ажурирајте позадинско знаењестуденти:
(Вовед во концептите на тангента и нормално на крива)
Знаеме аналитички и физичко значењедериват: (одговара на ученикот :
аналитичкото значење е, физичкото значење е брзината на процесот одредена од функцијата).
Дозволете ни да го дознаеме геометриското значење на дериватот.
За да го направите ова, го воведуваме концептот на тангента на крива во дадена точка.
Од училишен курсгеометрија, го знаеш концептот на тангента на круг. (одговара на ученикот : тангента на кружница се дефинира како права линија која лежи во иста рамнина како и кругот и има единствена заедничка точка со неа).
Но, таквата дефиниција за тангента не е применлива за случајот на произволна крива. На пример, за парабола, оските имаат по една заедничка точкасо парабола. Сепак, оската е тангента на параболата, но оската не е. Ајде да дадеме општа дефиницијатангента на крива во дадена точка.
Некои точки на произволна крива нека бидат секант на кривата. Како што се приближува точка по крива, секантата ќе се ротира околу точката
Дефиниција. Ограничувачката положба на секанта за неограничен пристап на точка долж кривата се нарекуватангента до кривата во точката
Дефиниција . Нормално на крива во точка е права линија што минува низ точката нормална на тангентата на кривата во таа точка.
Ако е тангента на кривата во точка,
тогаш нормалната ќе биде нормална на кривата во точката
Објаснување на новиот материјал:
(Ајде да дознаеме кое е геометриското значење на дериватот , какви својства имаат аголните коефициенти на тангентата и нормалата?
Нека кривата е график на функција. Поени
лежат на графикот на функцијата. Правата линија е тангента на крива.
Тангентен агол
Изводот на функцијата во точка е еднаков на тангентата на аголот на наклонетост на тангентата нацртана во точката или наклонот на тангентата на графикот на функцијата во оваа точка .
Тангентна равенка до кривата во точка има форма
Нормална равенка до кривата во точка има форма
(3)
Проблематични прашања : погледнете ги тангентите и нормалните равенки, кои се нивните разлики и сличности?
На што е еднаков производот? Зошто се случува ова?
(Учениците мора да ги дадат следните одговори на прашањата: -1, бидејќи тангентата и нормалата се меѓусебно нормални)
Консолидација на теоретскиот материјал во пракса:
( Решавање проблеми во училницата)
Пример 1. Пресметај ги аголните коефициенти на тангентите на параболата во точките.
Решение. Од геометриското значење на дериватот (формула 1) наклонот на тангентата.
Да го најдеме изводот на функцијата: .
. Оттука,.
Да ја најдеме вредноста на изводот во точката
Оттука,.
Пример 2. Тангентите на параболата се нацртани на точките Најди ги аглите на наклонетост на тангентите на оската Окс.
Решение. Според формулата (1)
Ајде да го најдеме. .
Да ја пресметаме вредноста на изводот во точката: .
Затоа, и.
Исто и во точката.
Затоа, и
Пример 3. Во која точка тангентата на кривата е наклонета кон оската Ox?
под агол
Решение. Според формулата (1)
; . Затоа, и
Заменувајќи се во функцијата, добиваме. Ја сфативме поентата.
Пример 4. Напиши равенка за тангентата и нормалната на параболата во една точка
Решение. Равенката за тангента на крива е:
Од проблематичните услови. Ајде да го најдеме дериватот.
; .
Заменувајќи ги сите вредности во равенката, ја добиваме тангентата равенка
или.
Ајде да создадеме нормална равенка користејќи ја формулата:
или
Задачи за независна одлука:
1. Најдете го аголниот коефициент на тангентата нацртана на кривата во точката.
2. Кривата е дадена со равенката Определете ги аглите на наклонетост на тангентите кон позитивната насока на оската нацртана кон кривата во точките на точките со апсциса.
3. Најдете ја точката на кривата во која тангентата е паралелна на правата.
4. Во која точка е тангентата на кривата: а) паралелна со оската; б) формира агол од 45 со оската?
5. Најдете ја апсцисата на точката на параболата во која тангентата е паралелна со оската на апсцисата.
6. Најдете го аголниот коефициент на тангентата нацртана на кривата во точката.
7. Во која точка тангентата на кривата формира агол од 30 со оската?
8. Во која точка тангентата на графикот на функцијата формира агол од 135
со оска?
9. Во која точка тангентата на графикот на функцијата е паралелна со оската x?
10. Во кои точки аголниот коефициент на тангента на кубна парабола е еднаков на 3?
11. Најдете го аголот на наклонетост на тангентата на кривата во точката чија апсциса е еднаква на 2.
12. Направете равенка за тангентата на параболата во точката со апсцисата
13. Направете равенка за тангентата на хиперболата во точка
14. Направете равенка за тангента на крива во точка.
15. Најдете ја тангентата на кривата во точката со апсцисата.
Одговори : 1) .12 2). 45°,арктг 5 3) .(1;1) 4) .(0;-1) (0,5;-0,75) 5) .1/2 6) .1 7) .(/6;61/12) 8) .(0:-1) (4;3) 9) .(0;4) (1;-5) 10) .(1;1) (-1;-1) 11) . 45°12) .y = -2x-113) .y = -x+214) .y=4x+615) .y = 4x-2.
Критериум за евалуација : "5" - 15 задачи
"4" - 11-14 задачи
"3" - 8 задачи
4. Резиме на лекција : оценување; + и – лекција за ученикот (што разбравте и што сè уште треба да се разбере?)
5. Домашна задача: подгответе одговори на прашањата:
Дефинирајте тангента на крива.
Што е нормално за крива?
Кое е геометриското значење на дериватот? Запишете ја формулата.
Запишете ја равенката на тангентата на кривата во оваа точка.
Запишете ја равенката на нормалата на кривата во оваа точка.
Решавање на проблеми 1-15 за избор на критериум за оценување;дополнително на барање : направи и реши картичка на оваа тема.
Нормална равенка во општ погледнапишано како:
Ако функцијата е наведена во параметарска форма x(t) , y(t) , тогаш нормалната равенка се наоѓа со помош на формулата:
(x–x 0)x’+(y-y 0)y’=0
Цел на услугата. Оваа услуга е дизајнирана да пронајде равенки од нормала до крива. Решението е изготвено во Word формат. За да се добие равенката, потребно е да се избере типот на дадената функција.
Алгоритам за составување на равенката на нормалата на графикот на функцијата
- Пресметка на вредноста на функцијата y 0 во точката x 0: y 0 = f(x 0). Ако е наведена почетната вредност y 0, тогаш продолжете до чекор 2.
- Наоѓање на изводот y"(x).
- Пресметка на вредноста на изводот на x 0.
- Запишување на равенката на нормалата на крива линија во форма: y k = y 0 - 1/y"(y 0)(x - x 0)
Пример Задача бр. 1
Најдете ја равенката на нормалата на параболата y = 1/2*x 2 во точката (-2;2).
Решениенајдете со помош на калкулатор.
Да ги напишеме нормалните равенки во општа форма: ![]()
Според условите на задачата x 0 = -2, тогаш y 0 = 2
Сега да го најдеме дериватот:
y" = (1 / 2 x 2)" = x
оттука:
f"(-2) = -2 = -2
Како резултат имаме: ![]()
или
y k = 1 / 2 x+3
Задача бр. 2
Напиши ги равенките на нормалата на кривата y 2 -1/2*x 3 -8 во точката M 0 (0;2).
Решение.
Бидејќи функцијата е имплицитно наведена, го бараме изводот користејќи ја формулата: 
За нашата функција: ![]()
Потоа: 
или
оттука:
F x "(0;2) = 3 / 4 0 2 / 2 = 0
Како резултат имаме: ![]()
или
x = 0
Задача бр.3
Напиши ги равенките на нормалата на елипсата дадени во параметарски облик: x = 5*sqrt(2)*cos(t);y = 3*sqrt(2)*sin(t) во точката M 0 (-5;3 ).
Решение.
Дозволете ни да ги напишеме нормалните равенки за функцијата одредена во параметарска форма:
(x - x 0)x" + (y - y 0)y" = 0
Оваа точка M 0 (-5;3) одговара на вредноста t = 3 / 4 π
За нашата функција: ![]()
![]()
оттука:
Како резултат имаме:
(x +5)-5 + (y - 3)-3 = 0
или
y k = -5x-3y-16
Како да се најде равенката на нормалата на графикот на функција во дадена точка?
Во оваа лекција ќе научиме како да ја најдеме равенката на нормалното до функционален график во точка и погледнете бројни примери кои се однесуваат на овој проблем. За правилно да го асимилирате материјалот, треба да разберете геометриско значење на дериватот и да можете да ги најдете барем на ниво на следните статии:
Како да се најде дериватот? Извод на сложена функција И .
Наведените лекции ќе им овозможат на „куклите“ брзо да се движат на темата и да ги подобрат своите вештини за диференцијација речиси од нула. целосна нула. Во суштина, она што следи сега е детално продолжение на ставот за тангентна равенка 3-та статија од горната листа. Зошто продолжение? Нормалната равенка е тесно поврзана со тангентата равенка. Меѓу другото, ќе разгледам проблеми за тоа како да се конструираат равенки за овие линии во ситуации кога функцијата е специфицирано имплицитно или параметарски .
Но, прво, да ги освежиме нашите сеќавања: ако функцијата диференцијабилна во точка (т.е. ако има конечнаизвод), тогаш равенката на тангентата на графикот на функцијата во точка може да се најде со помош на следнава формула:
Ова е најчестиот случај што веќе го сретнавме во лекцијата. Наједноставните проблеми со деривати . Меѓутоа, материјата не е ограничена на ова: ако во точка има бесконечен извод: , тогаш тангентата ќе биде паралелна со оската и нејзината равенка ќе добие форма . Стандарден пример: функција со извод што оди до бесконечност во близина критична точка . Соодветната тангента ќе се изрази со равенката: (оска на ординати).
Ако изводот не постои (на пример, дериват на во точка), тогаш, се разбира, не постои и заедничка тангента .
Ќе ви кажам како да направите разлика помеѓу последните два случаи малку подоцна, но засега да се вратиме на главниот тек на денешната лекција:
Што е нормално? Нормално до графикот на функцијата во точка се повикува директно , поминувајќи низ дадена точка нормална на тангентата на графикот на функцијата во оваа точка (јасно е дека тангентата мора да постои). Накратко, нормала е права нормална на тангентата и минува низ точката на тангенција.
Како да се најде нормалната равенка? Од курс по аналитичка геометрија се сугерира многу едноставен алгоритам: наоѓаме тангентна равенка и презентирајте го на општ поглед . Следно „отстрануваме“ нормален вектор и состави ја равенката на нормалата во точката и векторот на насоката.
Овој метод може да се користи, но во математичката анализа вообичаено е да се користи готова формула заснована на односи меѓу аголните коефициенти на нормални прави
. Доколку постои конечнаИ не-нулаизвод, тогаш равенката на нормалата на графикот на функцијата во точка се изразува со следнава равенка: ![]()
Дефинитивно ќе разгледаме посебни случаи кога е еднакво на нула или бесконечност, но прво, „обични“ примери:
Пример 1
Напиши равенки за тангентата и нормалната на графикот на кривата ![]() во точката чија апсциса е еднаква на .
во точката чија апсциса е еднаква на .
Во практичните задачи, честопати треба да ја пронајдете и тангентата линија. Сепак, ова е само за рака - би било подобро да има „полна рака“ =)
Решение: Првиот дел од задачата е добро познат, ајде да ја составиме тангентата равенка користејќи ја формулата:
Во овој случај: 
Ајде да најдеме дериват
:
 Еве на првиот чекор ја помести константата надвор од знакот на дериватот
, на вториот – користен правило за диференцирање сложена функција
.
Еве на првиот чекор ја помести константата надвор од знакот на дериватот
, на вториот – користен правило за диференцирање сложена функција
.
Сега да пресметаме извод во точка :
Примено конечен броји тоа ме прави среќен. Ајде да го замениме во формулата:
![]()
Ајде да го преместиме на врвот на левата страна, да ги отвориме заградите и да ја претставиме тангентата равенка во општ поглед
:
 Вториот дел од задачата не е потежок. Ајде да ја составиме нормалната равенка користејќи ја формулата:
Вториот дел од задачата не е потежок. Ајде да ја составиме нормалната равенка користејќи ја формулата:  Ослободување од трикатна дропка
и донесете ја на ум равенката:
Ослободување од трикатна дропка
и донесете ја на ум равенката: ![]() – потребната равенка.
– потребната равенка.
Одговори:
Овде можете да извршите делумна проверка. Прво, координатите на точката мора да ја задоволуваат секоја равенка:
![]() - вистинска еднаквост.
- вистинска еднаквост.
![]() - вистинска еднаквост.
- вистинска еднаквост.
И второ, нормални вектори мора да биде ортогонален. Ова може лесно да се потврди со користење производ со точки : , што е она што требаше да се провери.
Алтернативно, наместо нормални вектори можете да ги користите насока вектори на прави линии .
! Оваа проверка се покажува како бескорисна ако изводот и/или изводот во точката се погрешно пронајдени. Ова е „слабата алка“ на задачата - бидете исклучително внимателни!
Не беше потребен цртеж, но заради комплетноста:  Смешно е, но всушност е добиена целосна проверка, бидејќи цртежот е направен сосема точно =) Патем, функцијата
Смешно е, но всушност е добиена целосна проверка, бидејќи цртежот е направен сосема точно =) Патем, функцијата ![]() го поставува горниот лак елипса
.
го поставува горниот лак елипса
.
Следната задача треба да ја решите сами:
Пример 2
Запишете ги равенките за тангентата и нормалната на графикот на функцијата во точката .
Приближен примерок од завршната задача на крајот од лекцијата.
Сега да погледнеме два посебни случаи:
1) Ако изводот во точка е еднаков на нула: , тогаш тангентната равенка ќе се поедностави:  Тоа е, тангентата ќе биде паралелна со оската.
Тоа е, тангентата ќе биде паралелна со оската.
Соодветно на тоа, нормалата ќе помине низ точката паралелна на оската, што значи дека нејзината равенка ќе ја добие формата.
2) Ако изводот во точка постои, но е бесконечен: , тогаш, како што е забележано на самиот почеток на членот, тангентата ќе стане вертикална: . И бидејќи нормалата минува низ точката паралелна со оската, нејзината равенка ќе биде изразена на „огледало“:
Едноставно е:
Пример 3
Напиши равенки за тангента и нормална на парабола ![]() во точка. Направете цртеж.
во точка. Направете цртеж.
Не го додадов барањето за завршување на цртежот - вака беше формулирана задачата во оригиналот. Иако ова е ретко.
Решение: ајде да создадеме равенка за тангентата. Во овој случај
Се чини дека пресметките се тривијални, но повеќе од можно е да се збуни во знаците: 
Така: ![]()
Бидејќи тангентата е паралелна со оската (Случај бр. 1), тогаш нормалното минување низ истата точка ќе биде паралелно со оската на ординатите:
Цртежот е, се разбира, дополнителна неволја, но е добра проверка на аналитичкото решение: 
Одговори: ,
Во училишните курсеви по математика, вообичаена е поедноставена дефиниција за тангента, која е формулирана вака: „Тангента на графикон на функција е права која има единствена заедничка точка со дадениот график“. Како што можете да видите, во општ случај оваа изјава е неточна. Според геометриско значење на дериватот , тангентата е зелената линија, а не сината линија.
Следниот пример е посветен на истиот случај бр. 1, кога:
Пример 4
Напишете ја равенката на тангентата и нормалната на кривата во точката.
Кратко решение и одговор на крајот од часот
Случај бр.2, во кој ретко се појавува во пракса, па почетниците не треба премногу да се грижат и со лесно срце да го прескокнат петтиот пример. Информациите со курзив се наменети за напредни читатели кои добро ги разбираат дефиниции за дериват и тангента и исто така имаат искуство наоѓање на дериватот по дефиниција :
Пример 5
Најдете ги равенките на тангентата и нормалната на графикот на функцијата во точка
Решение
: Вкритична точка
дериват именител ![]() исчезнува, и затоа тука треба да пресметате еднострани деривати користејќи ја дефиницијата за дериват (видете го крајот на статијатаДериват по дефиниција
):
исчезнува, и затоа тука треба да пресметате еднострани деривати користејќи ја дефиницијата за дериват (видете го крајот на статијатаДериват по дефиниција
):
 Двата деривати се бесконечни, затоа, во точката постои заедничка вертикална тангента:
Па, очигледно е дека х-оската е нормална. Формално, според формулата:
За подобро разбирање на проблемот, еве еден цртеж:
Двата деривати се бесконечни, затоа, во точката постои заедничка вертикална тангента:
Па, очигледно е дека х-оската е нормална. Формално, според формулата:
За подобро разбирање на проблемот, еве еден цртеж:
 Одговори
:
Одговори
:
Мило ми е што не отидовте да сурфате на Интернет, бидејќи целата забава допрва започнува! За да го совладате материјалот во следниот пасус, треба да бидете во можност да најдете извод на имплицитна функција :
Како да се најде тангентата равенка и нормалната равенка ако функцијата е имплицитно одредена?
Формулите тангента и нормалната остануваат исти, но техниката на решение се менува:
Пример 6
Најдете ги равенките на тангентата и нормалната на кривата во точката.
Решение: судејќи според равенката, ова е некој вид Линија од 3 ред , која точно сега воопшто не не интересира.
Има малициозен софтвер во равенката, па така и изгледите за изразување на функцијата во експлицитноизгледа прилично магливо.
Но, ова не е потребно! Има многу погенијално решение. Ајде да ја составиме тангентата равенка користејќи ја истата формула.
Вредностите се познати од условот, патем, не е повредено да се осигураме дека тие навистина ја задоволуваат предложената равенка:  Се добива правилна еднаквост, што значи дека се е во ред со точката.
Се добива правилна еднаквост, што значи дека се е во ред со точката.
Останува само да се пресмета. Прво, користејќи ја стандардната шема, наоѓаме извод на функција назначена имплицитно
:

Дозволете ни да го преработиме резултатот со ознака посоодветна за нашата задача: ![]()
На вториот чекор, го заменуваме : во пронајдениот изводен израз:
Тоа е тоа!
Останува само внимателно да се разбере равенката: 
Ајде да создадеме нормална равенка: 
Одговори:
Подготвени! И на почетокот сè изгледаше тешко. Иако дериватот овде, се разбира, е ранливо место. Сликичка за само-решение:
Пример 7
Најдете ја равенката на нормалата на права во точка
Доста е веќе со тангентата =)
Во овој случај, лесно е да се открие што е тоа круг
центар во точката на радиусот и дури и ја изразуваат саканата функција ![]() . Но зошто?! На крајот на краиштата, пронајдете го дериватот на имплицитна функција
многу полесно! Таа е скоро најпримитивна овде.
. Но зошто?! На крајот на краиштата, пронајдете го дериватот на имплицитна функција
многу полесно! Таа е скоро најпримитивна овде.
Кратко решение и одговор на крајот од часот.
Како да се најде тангентата равенка и нормалната равенка ако функцијата е наведена параметарски?
Уште полесно. Но, за ова треба да вежбате пронаоѓање извод на параметарски одредена функција . И ова е речиси бесплатно:
Пример 8
Нацртај равенки за тангентата и нормалната на циклоидот нацртан во точката за која .
На страницата може да се најде цртеж на циклоидот S и V, ако линијата е наведена параметарски (се случува овој напис да е создаден порано). Ја покажува дури и допирната точка.
Решение: Апсцисата и ординатата на тангентата точка се пресметуваат директно од параметарските равенки на кривата: 
Ајде да најдеме 1. извод на параметарски дефинирана функција :
И да ја пресметаме неговата вредност на: 
Ајде да ја составиме тангентната равенка користејќи ја вообичаената формула, приспособена за малку различни ознаки: 
Нормална равенка: 
Одговори:
Како заклучок, предлагам да се запознаете со уште една интересна линија:
Пример 9
Напишете равенка за нормалната на полукубна парабола нацртана во точката за која .
Ова е пример за да го решите сами. Дозволете ми да ве потсетам дека графиконите на параметарски одредени функции може да се конструираат, на пример, со користење на my дизајн геометриски распоред .
Па, нашата лекција заврши и се надевам дека презентираниот материјал не беше тангенцијален за вас, туку нормален =)
Ви благодариме за вниманието и со среќа!
Решенија и одговори:
Пример 2:Решение
Во овој случај:
 Така:
Така:
 Ајде да ја составиме нормалната равенка користејќи ја формулата
Ајде да ја составиме нормалната равенка користејќи ја формулата ![]() :
:
 Одговори
:
Одговори
:
Пример 4:Решение
: ајде да ја составиме тангентата равенка користејќи ја формулата:
Во оваа задача:
 Така:
Така:
 Во одредена точка, тангентата е паралелна со оската, така што соодветната нормална равенка е:
Одговори
:
Во одредена точка, тангентата е паралелна со оската, така што соодветната нормална равенка е:
Одговори
:
Пример 7:Решение
: во овој проблем: .
Ајде да го најдеме дериватот:
 Или:
Ајде да го замениме изводот во изразот:
Или:
Ајде да го замениме изводот во изразот:
![]() Потребната нормална равенка:
Потребната нормална равенка:
 Одговори
:
Одговори
:
Пример 9:Решение
: во овој случај:
![]() Ајде да го најдеме изводот и да ја пресметаме неговата вредност на:
Ајде да го најдеме изводот и да ја пресметаме неговата вредност на:
 Нормална равенка:
Нормална равенка:
 Одговори
:
Одговори
:
Преземено од страницата http://www.mathprofi.ru