Најдете ја проекцијата на векторот a на координатните оски. Линеарни операции на вектори. Теореми за векторска проекција

Решавањето на проблемите за рамнотежата на силите што се конвергираат со конструирање полигони со затворена сила вклучува гломазни конструкции. Универзален метод за решавање на вакви проблеми е да се премине кон одредување на проекциите на дадените сили на координатните оски и работење со овие проекции. Оската е права линија на која и е доделена одредена насока.

Проекцијата на векторот на оската е скаларна величина, која се определува со сегментот на оската отсечен од нормалните спуштени на неа од почетокот и крајот на векторот.

Векторската проекција се смета за позитивна ако насоката од почетокот на проекцијата до нејзиниот крај се совпаѓа со позитивната насока на оската. Векторската проекција се смета за негативна ако насоката од почетокот на проекцијата до нејзиниот крај е спротивна на позитивната насока на оската.

Така, проекцијата на силата на координатната оска е еднаква на производот на модулот на сила и косинус на аголот помеѓу векторот на сила и позитивната насока на оската.

Да разгледаме голем број случаи на проектирање сили на оска:

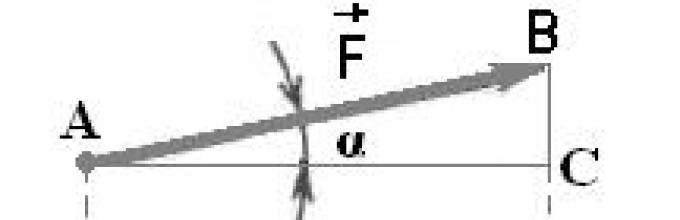
Вектор на сила Ф(сл. 15) прави остар агол со позитивната насока на оската x.

За да ја пронајдеме проекцијата, од почетокот и крајот на векторот на сила ги спуштаме нормалните на оската ох; добиваме

1. Fx = Ф cos α

Проекцијата на векторот во овој случај е позитивна

Сила Ф(сл. 16) е со позитивна насока на оската Xтап агол α.

Потоа Ф x = Ф cos α, но бидејќи α = 180 0 - φ,

Ф x = Ф cos α = Ф cos180 0 - φ =- Ф cos φ.

Проекција на сила Фпо оска охво овој случај тоа е негативно.

Сила Ф(сл. 17) нормално на оската ох.

Проекција на силата F на оската Xеднаква на нула

Ф x = Ф cos 90° = 0.

Сила лоцирана во авионот како(сл. 18), може да се проектира на две координатни оски ОИ ОУ.

Сила Фможе да се подели на компоненти: Ф x и Ф y. Векторски модул Ф x е еднаква на проекцијата на векторот Фпо оска вол, и векторскиот модул Ф y е еднаква на проекцијата на векторот Фпо оска ох.

Од Δ OAV: Ф x = Ф cos α, Ф x = Фгрев α.

Од Δ OAS: Ф x = Ф cos φ, Ф x = Фгрев φ.

Големината на силата може да се најде со помош на Питагоровата теорема:

Проекцијата на векторска сума или резултант на која било оска е еднаква на алгебарскиот збир на проекциите на збировите на векторите на истата оска.

Размислете за силите што се спојуваат Ф 1 , Ф 2 , Ф 3, и Ф 4, (сл. 19, а). Геометрискиот збир, или резултатот, на овие сили Фопределена со страната на затворање на силниот многуаголник

Да паднеме од темињата на многуаголникот на силата до оската xперпендикулари.

Со оглед на добиените проекции на сили директно од завршената конструкција имаме

Ф= Ф 1x+ Ф 2x+ Ф 3x+ Ф 4x

каде n е бројот на векторски членови. Нивните проекции влегуваат во горната равенка со соодветниот знак.

Во рамнина, геометрискиот збир на сили може да се проектира на две координатни оски, а во просторот, соодветно, на три.

Прво, да се потсетиме што е тоа координатна оска, проекција на точка на оскаИ координати на точка на оската.

Координатна оска- Ова е права линија на која и се дава некаков правец. Можете да го замислите како вектор со бескрајно голем модул.

Координатна оскаозначено со некоја буква: X, Y, Z, s, t... Обично на оската (произволно) се избира точка која се нарекува почеток и по правило се означува со буквата O. Од оваа точка се мерат растојанија до други точки од интерес за нас.

Проекција на точка на оска- ова е основата на нормалната спуштена од оваа точка до оваа оска (сл. 8). Односно, проекцијата на точка на оската е точка.

Точка координата на оската- ова е број чија апсолутна вредност е еднаква на должината на сегментот на оската (на избраната скала) содржан помеѓу потеклото на оската и проекцијата на точката на оваа оска. Овој број се зема со знак плус ако проекцијата на точката се наоѓа во правец на оската од нејзиното потекло и со знак минус ако е во спротивна насока.

Скаларна проекција на вектор на оска- Ова број, чија апсолутна вредност е еднаква на должината на сегментот на оската (на избраната скала) затворен помеѓу проекциите на почетната точка и крајната точка на векторот. Важно! Обично наместо изразот скаларна проекција на вектор на оскатие едноставно велат - проекција на векторот на оската, односно зборот скаларенспуштена. Векторска проекцијасе означува со истата буква како проектираниот вектор (во нормално, незадебелено пишување), со помал (по правило) индекс на името на оската на која е проектиран овој вектор. На пример, ако вектор е проектиран на оската X А,тогаш неговата проекција се означува со x. При проектирање на истиот вектор на друга оска, да речеме, на оската Y, неговата проекција ќе биде означена со y (сл. 9).

Да се пресмета проекција на векторот на оската(на пример, оската X), потребно е да се одземе координатата на почетната точка од координатата на нејзината крајна точка, т.е.

a x = x k − x n.

Треба да запомниме: скаларната проекција на вектор на оска (или, едноставно, проекцијата на вектор на оска) е број (не вектор)!Освен тоа, проекцијата може да биде позитивна ако вредноста x k е поголема од вредноста x n, негативна ако вредноста x k е помала од вредноста x n и еднаква на нула ако x k е еднаква на x n (сл. 10).

Проекцијата на векторот на оската може да се најде и со познавање на модулот на векторот и аголот што го прави со оваа оска.

Од Слика 11 е јасно дека a x = a Cos α

Односно, проекцијата на векторот на оската е еднаква на производот на модулот на векторот и косинусот на аголот помеѓу насоката на оската и насоката на векторот. Ако аголот е остар, тогаш Cos α > 0 и a x > 0, а ако е тап, тогаш косинусот на тапиот агол е негативен, а проекцијата на векторот на оската исто така ќе биде негативна.

Аглите измерени од оската спротивно од стрелките на часовникот се сметаат за позитивни, а аглите измерени долж оската се негативни. Меѓутоа, бидејќи косинус е парна функција, односно Cos α = Cos (− α), кога се пресметуваат проекциите, аглите може да се бројат и во насока на стрелките на часовникот и спротивно од стрелките на часовникот.

При решавање на проблеми често ќе се користат следните својства на проекциите: ако

А = б + в +…+ г, потоа a x = b x + c x +…+ d x (слично на другите оски),

а= m б, тогаш a x = mb x (слично за другите оски).

Формулата a x = a Cos α ќе биде Честосе јавуваат кога решавате проблеми, па дефинитивно треба да го знаете тоа. Треба да го знаете правилото за одредување на проекцијата напамет!

Запомнете!

За да се најде проекцијата на векторот на оската, модулот на овој вектор мора да се помножи со косинус на аголот помеѓу насоката на оската и насоката на векторот.

Уште еднаш - напамет!

Проекцијавектор на оска е вектор кој се добива со множење на скаларната проекција на векторот на оваа оска и единечниот вектор на оваа оска. На пример, ако x - скаларна проекцијавектор Адо оската X, потоа x јас- неговата векторска проекција на оваа оска.

Да означиме векторска проекцијаисто како и самиот вектор, но со индекс на оската на која е проектиран векторот. Значи, векторската проекција на векторот Ана X оската што ја означуваме А x( мастибуква што означува вектор и знак на името на оската) или (незадебелена буква што означува вектор, но со стрелка на врвот (!) и знак на името на оската).

Скаларна проекцијавектор по оска се нарекува број, чија апсолутна вредност е еднаква на должината на сегментот на оската (на избраната скала) затворен помеѓу проекциите на почетната точка и крајната точка на векторот. Обично наместо изразот скаларна проекцијатие едноставно велат - проекција. Проекцијата се означува со истата буква како и проектираниот вектор (во нормално, незадебелено пишување), со помал индекс (по правило) на името на оската на која се проектира овој вектор. На пример, ако вектор е проектиран на оската X А,тогаш неговата проекција се означува со x. При проектирање на истиот вектор на друга оска, ако оската е Y, нејзината проекција ќе биде означена со y.

Да се пресмета проекцијата векторна оската (на пример, оската X), потребно е да се одземе координатата на почетната точка од координатата на нејзината крајна точка, т.е.
a x = x k − x n.
Проекцијата на вектор на оска е бројка.Покрај тоа, проекцијата може да биде позитивна ако вредноста x k е поголема од вредноста x n,

негативен ако вредноста x k е помала од вредноста x n

и еднакво на нула ако x k е еднакво на x n.

Проекцијата на векторот на оската може да се најде и со познавање на модулот на векторот и аголот што го прави со оваа оска.

Од сликата е јасно дека a x = a Cos α

односно, проекцијата на векторот на оската е еднаква на производот од модулот на векторот и косинусот на аголот помеѓу насоката на оската и векторска насока. Ако аголот е акутен, тогаш
Cos α > 0 и a x > 0, и ако е тап, тогаш косинусот на тапиот агол е негативен, а проекцијата на векторот на оската исто така ќе биде негативна.

Векторски координати— коефициенти на единствената можна линеарна комбинација на основни вектори во избраниот координатен систем, еднакви на дадениот вектор.

каде се координатите на векторот.

Точка производ на вектори

Скаларен производ на вектори[- во конечни-димензионални векторски просторсе дефинира како збир од производите на идентични компоненти што се множат вектори.

На пример, S.p.v. а = (а 1 , ..., a n) И б = (б 1 , ..., b n):

(а , б ) = а 1 б 1 + а 2 б 2 + ... + a n b n

По физика за 9 одделение (I.K.Kikoin, A.K.Kikoin, 1999),
задача №5
до поглавјето " ГЛАВА 1. ОПШТИ ИНФОРМАЦИИ ЗА СООБРАЌАЈ».

1. Како се нарекува проекција на вектор на координатната оска?

1. Проекцијата на векторот a на координатната оска е должината на отсечката помеѓу проекциите на почетокот и крајот на векторот a (нормални паднати од овие точки на оската) на оваа координатна оска.

2. Како е поврзан векторот на поместување на телото со неговите координати?

2. Проекциите на векторот на поместување s на координатните оски се еднакви на промената на соодветните координати на телото.

3. Ако координатата на точката се зголемува со текот на времето, тогаш каков знак има проекцијата на векторот на поместување на координатната оска? Што ако се намали?

3. Ако координатата на точката се зголемува со текот на времето, тогаш проекцијата на векторот на поместување на координатната оска ќе биде позитивна, бидејќи во овој случај ќе преминеме од проекцијата на почетокот до проекцијата на крајот на векторот во правец на самата оска.

Ако координатата на точката се намалува со текот на времето, тогаш проекцијата на векторот на поместување на координатната оска ќе биде негативна, бидејќи во овој случај ќе преминеме од проекцијата на почетокот до проекцијата на крајот на векторот наспроти водилката на самата оска.

4. Ако векторот на поместување е паралелен со оската X, тогаш колкав е модулот на проекцијата на векторот на оваа оска? А што е со модулот на проекцијата на истиот вектор на оската Y?

4. Ако векторот на поместување е паралелен со оската X, тогаш модулот на проекцијата на векторот на оваа оска е еднаков на модулот на самиот вектор, а неговата проекција на оската Y е нула.

5. Определете ги знаците на проекциите на X оската на векторите на поместување прикажани на слика 22. Како се менуваат координатите на телото за време на овие поместувања?

5. Во сите следни случаи, Y координатата на телото не се менува, а X координатата на телото ќе се промени на следниов начин:

а) s 1;

проекцијата на векторот s 1 на оската X е негативна и по апсолутна вредност е еднаква на должината на векторот s 1 . Со такво движење, X координатата на телото ќе се намали за должината на векторот s 1.

б) s 2 ;

проекцијата на векторот s 2 на оската X е позитивна и еднаква по големина на должината на векторот s 1 . Со такво движење, X координатата на телото ќе се зголеми за должината на векторот s 2.

в) s 3 ;

проекцијата на векторот s 3 на оската X е негативна и еднаква по големина на должината на векторот s 3 . Со такво движење, X координатата на телото ќе се намали за должината на векторот s 3.

г)с 4;

проекцијата на векторот s 4 на оската X е позитивна и еднаква по големина на должината на векторот s 4 . Со такво движење, X координатата на телото ќе се зголеми за должината на векторот s 4.

д) s 5;

проекцијата на векторот s 5 на оската X е негативна и еднаква по големина на должината на векторот s 5 . Со такво движење, X координатата на телото ќе се намали за должината на векторот s 5.

6. Ако вредноста на поминатото растојание е голема, тогаш модулот за поместување може да биде мал?

6. Можеби. Ова се должи на фактот дека поместувањето (вектор на поместување) е векторска величина, т.е. е насочен праволиниски сегмент кој ја поврзува почетната положба на телото со неговите последователни позиции. И крајната положба на телото (без разлика на поминатото растојание) може да биде колку што сакате поблиску до почетната положба на телото. Ако крајната и почетната положба на телото се совпаѓаат, модулот за поместување ќе биде еднаков на нула.

7. Зошто векторот на движење на телото е поважен во механиката од патот што го поминал?

7. Главната задача на механиката е да ја одреди положбата на телото во секое време. Познавајќи го векторот на движење на телото, можеме да ги одредиме координатите на телото, т.е. положбата на телото во секој момент во времето, а знаејќи го само поминатото растојание, не можеме да ги одредиме координатите на телото, бидејќи немаме информации за правецот на движење, туку можеме само да ја процениме должината на патеката помината во дадено време.

Оската е насоката. Ова значи дека проекцијата на оска или на насочена линија се смета за иста. Проекцијата може да биде алгебарска или геометриска. Во геометриска смисла, проекцијата на вектор на оска се подразбира како вектор, а во алгебарска смисла, како број. Односно, се користат концептите на проекција на вектор на оска и нумеричка проекција на вектор на оска.

Ако имаме L оска и ненулти вектор A B →, тогаш можеме да конструираме вектор A 1 B 1 ⇀, означувајќи ги проекциите на неговите точки A 1 и B 1.

A 1 B → 1 ќе биде проекцијата на векторот A B → на L.

Дефиниција 1

Проекција на векторот на оскатае вектор чиј почеток и крај се проекции на почетокот и крајот на даден вектор. n p L A B → → вообичаено е да се означи проекцијата A B → на L. За да се изгради проекција на L, нормалните се спуштаат на L.

Пример 1

Пример за векторска проекција на оска.

На координатната рамнина O x y е наведена точка M 1 (x 1, y 1). Потребно е да се конструираат проекции на O x и O y за да се прикаже векторот на радиусот на точката M 1. Ги добиваме координатите на векторите (x 1, 0) и (0, y 1).

Ако зборуваме за проекцијата на a → на ненула b → или за проекцијата на a → на насоката b → , тогаш се мисли на проекцијата на a → на оската со која насоката b → се совпаѓа. Проекцијата на a → на линијата дефинирана со b → е означена n p b → a → → . Познато е дека кога аголот помеѓу a → и b → , n p b → a → → и b → може да се смета за конасочен. Во случај кога аголот е тап, n p b → a → → и b → се во спротивни насоки. Во ситуација на перпендикуларност a → и b →, а a → е нула, проекцијата на a → во насока b → е нулта вектор.

Нумеричката карактеристика на проекцијата на вектор на оска е нумеричката проекција на вектор на дадена оска.

Дефиниција 2

Нумеричка проекција на векторот на оскатае број кој е еднаков на производот од должината на даден вектор и косинус на аголот помеѓу дадениот вектор и векторот што ја одредува насоката на оската.

Нумеричката проекција на A B → на L се означува n p L A B → , и a → на b → - n p b → a → .

Врз основа на формулата добиваме n p b → a → = a → · cos a → , b → ^ , од каде a → е должината на векторот a → , a ⇀ , b → ^ е аголот помеѓу векторите a → и b → .

Ја добиваме формулата за пресметување на нумеричката проекција: n p b → a → = a → · cos a → , b → ^ . Применливо е за познати должини a → и b → и аголот меѓу нив. Формулата е применлива за познати координати a → и b →, но постои поедноставена форма.

Пример 2

Откријте ја бројната проекција на a → на права линија во правец b → со должина a → еднаква на 8 и агол меѓу нив од 60 степени. По услов имаме ⇀ = 8, a ⇀, b → ^ = 60 °. Ова значи дека ги заменуваме нумеричките вредности во формулата n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4.

Одговор: 4.

Со познат cos (a → , b → ^) = a ⇀ , b → a → · b → , имаме a → , b → како скаларен производ на a → и b → . Следејќи ја формулата n p b → a → = a → · cos a ⇀ , b → ^ , можеме да ја најдеме нумеричката проекција a → насочена по векторот b → и да добиеме n p b → a → = a → , b → b → . Формулата е еквивалентна на дефиницијата дадена на почетокот на параграфот.

Дефиниција 3

Нумеричката проекција на векторот a → на оска што се совпаѓа во насока со b → е односот на скаларниот производ на векторите a → и b → до должината b → . Формулата n p b → a → = a → , b → b → е применлива за да се најде нумеричката проекција на a → на права што се совпаѓа во насока со b → , со познати a → и b → координати.

Пример 3

Дадено b → = (- 3 , 4) . Најдете ја нумеричката проекција a → = (1, 7) на L.

Решение

На координатната рамнина n p b → a → = a → , b → b → има форма n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , со a → = (a x , a y ) и b → = b x, b y. За да ја пронајдете нумеричката проекција на векторот a → на оската L, потребно е: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.

Одговор: 5.

Пример 4

Најдете ја проекцијата на a → на L, што се совпаѓа со насоката b →, каде што има a → = - 2, 3, 1 и b → = (3, - 2, 6). Наведен е тродимензионален простор.

Решение

Со оглед на a → = a x , a y , a z и b → = b x , b y , b z , го пресметуваме скаларниот производ: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Должината b → се наоѓа со помош на формулата b → = b x 2 + b y 2 + b z 2 . Следи дека формулата за определување на бројната проекција a → ќе биде: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .

Заменете ги нумеричките вредности: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .

Одговор: - 6 7.

Да ја погледнеме врската помеѓу a → на L и должината на проекцијата a → на L. Да нацртаме оска L, додавајќи → и b → од точка на L, по што цртаме нормална линија од крајот a → до L и нацртаме проекција на L. Постојат 5 варијации на сликата:

Првослучајот со a → = n p b → a → → значи a → = n p b → a → → , па оттука n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .

Второслучајот подразбира употреба на n p b → a → ⇀ = a → · cos a → , b → , што значи n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .

Третослучајот објаснува дека кога n p b → a → → = 0 → добиваме n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , тогаш n p b → a → → = 0 и n p b → a → = 0 = n p b → a → → .

Четвртослучајот покажува n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , следи n p b → a → = a → · cos ( a → , b → ^) = - n p b → a → → .

Петтослучајот покажува a → = n p b → a → → , што значи a → = n p b → a → → , оттука имаме n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - a → = - n p b → a → .

Дефиниција 4

Нумеричката проекција на векторот a → на оската L, која е насочена на ист начин како b →, ја има следната вредност:

должината на проекцијата на векторот a → на L, под услов аголот помеѓу a → и b → да биде помал од 90 степени или еднаков на 0: n p b → a → = n p b → a → → со условот 0 ≤ (a → , б →) ^< 90 ° ;
нула под услов a → и b → да се нормални: n p b → a → = 0, кога (a → , b → ^) = 90 °;
должината на проекцијата a → на L, помножена со -1, кога има тап или правилен агол на векторите a → и b →: n p b → a → = - n p b → a → → со услов од 90 °< a → , b → ^ ≤ 180 ° .

Пример 5

Со оглед на должината на проекцијата a → на L, еднаква на 2. Најдете ја бројната проекција a → под услов аголот да биде 5 π 6 радијани.

Решение

Од условот е јасно дека овој агол е тап: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .

Одговор: - 2.

Пример 6

Дадена е рамнина O x y z со векторска должина a → еднаква на 6 3, b → (- 2, 1, 2) со агол од 30 степени. Најдете ги координатите на проекцијата a → на оската L.

Решение

Прво, ја пресметуваме нумеричката проекција на векторот a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .

По услов, аголот е остар, тогаш нумеричката проекција a → = должината на проекцијата на векторот a →: n p L a → = n p L a → → = 9. Овој случај покажува дека векторите n p L a → → и b → се истонасочени, што значи дека има број t за кој е точно еднаквоста: n p L a → → = t · b → . Од тука гледаме дека n p L a → → = t · b → , што значи дека можеме да ја најдеме вредноста на параметарот t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .

Потоа n p L a → → = 3 · b → со координатите на проекцијата на векторот a → на оската L еднаква на b → = (- 2 , 1 , 2) , каде што е потребно да се помножат вредностите со 3. Имаме n p L a → → = (- 6 , 3 , 6) . Одговор: (- 6, 3, 6).

Потребно е да се повторат претходно научените информации за состојбата на колинеарност на векторите.

Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter