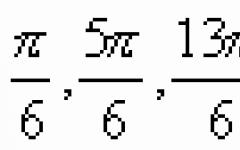И уште една точка: има доста формули за намалување на број, и веднаш ќе ве предупредиме да не ги научите сите напамет. Апсолутно нема потреба за ова - постои една која ви овозможува лесно да ги примените формулите за намалување.
Значи, да ги запишеме сите формули за намалување во форма на табела.

Овие формули може да се препишат со помош на степени и радијани. За да го направите ова, само запомнете ја врската помеѓу степените и радијаните и заменете го π со 180 степени насекаде.
Примери за користење на формули за намалување
Целта на овој став е да покаже како формулите за намалување се користат во пракса за решавање на примери.
За почеток, вреди да се каже дека има бесконечен број начини да се претстави агол под знакот на тригонометриски функции во форма и ![]() . Ова се должи на фактот дека аголот може да земе каква било вредност. Да го покажеме ова со пример.
. Ова се должи на фактот дека аголот може да земе каква било вредност. Да го покажеме ова со пример.
На пример, да го земеме аголот под знакот на тригонометриската функција еднаков на . Овој агол може да се претстави како ![]() , или што
, или што ![]() , или што
, или што ![]() , или на многу други начини.
, или на многу други начини.
Сега да видиме кои формули за намалување ќе треба да ги користиме во зависност од претставувањето на аголот. Ајде да земеме.
Ако аголот го претставиме како ![]() , тогаш оваа претстава одговара на формула за редукција на формата, од која добиваме
, тогаш оваа претстава одговара на формула за редукција на формата, од која добиваме  . Овде можеме да ја означиме вредноста на тригонометриската функција: .
. Овде можеме да ја означиме вредноста на тригонометриската функција: .
За презентација ![]() веќе ќе користиме формула на формата
веќе ќе користиме формула на формата ![]() , што не води до следниот резултат: .
, што не води до следниот резултат: .
Конечно, бидејќи соодветната формула за намалување ја има формата  .
.
За да ја завршиме оваа дискусија, особено вреди да се напомене дека постојат одредени погодности при користење на прикази на агли во кои аголот има вредност од 0 до 90 степени (од 0 до пи во половина радијани).
Ајде да погледнеме уште еден пример за користење на формули за намалување.
Пример.
Користејќи формули за редукција, претставувајте преку синус, а исто така и преку косинус на остар агол.
Решение.
За да ги примениме формулите за намалување, треба да претставиме агол од 197 степени во форма или ![]() , а според условите на проблемот, аголот мора да биде остар. Ова може да се направи на два начина:
, а според условите на проблемот, аголот мора да биде остар. Ова може да се направи на два начина: ![]() или . Така,
или . Така, ![]() или
или ![]() .
.
Осврнувајќи се на соодветните формули за намалување и , добиваме и .
Одговор:
![]() И
И ![]() .
.
Мнемоничко правило
Како што споменавме погоре, не е неопходно да се запаметат формулите за намалување. Ако ги погледнете внимателно, можете да идентификувате обрасци од кои можете да добиете правило кое ви овозможува да добиете која било од формулите за намалување. Му викаат мнемоничко правило(мнемониката е уметност на меморирање).
Менемоничкото правило содржи три фази:
Вреди да се каже веднаш дека за да го примените мнемоничкото правило, треба да бидете многу добри во идентификувањето на знаците на синус, косинус, тангента и котангента по четвртини, бидејќи тоа ќе мора постојано да го правите.
Ајде да ја разгледаме примената на мнемоничкото правило користејќи примери.
Пример.
Користејќи мнемоничко правило, запишете ги формулите за намалување за  И
И ![]() , земајќи го предвид аголот како агол на првата четвртина.
, земајќи го предвид аголот како агол на првата четвртина.
Решение.
Не мора да го правиме првиот чекор од правилото, бидејќи аглите под знаците на тригонометриските функции се веќе напишани во потребната форма.
Да го одредиме знакот на функциите  И
И ![]() . Под услов - аголот на првата четвртина, аголот
. Под услов - аголот на првата четвртина, аголот ![]() е и аголот на првата четвртина, а аголот
е и аголот на првата четвртина, а аголот ![]() - агол на втората четвртина. Косинусот во првата четвртина има знак плус, а тангентата во втората четвртина има знак минус. Во оваа фаза, потребните формули ќе имаат форма и . Сега кога ги сфативме знаците, можеме да продолжиме до последниот чекор од мнемоничкото правило.
- агол на втората четвртина. Косинусот во првата четвртина има знак плус, а тангентата во втората четвртина има знак минус. Во оваа фаза, потребните формули ќе имаат форма и . Сега кога ги сфативме знаците, можеме да продолжиме до последниот чекор од мнемоничкото правило.
Бидејќи аргументот на косинусната функција има форма ![]() , тогаш името на функцијата мора да се смени во кофункција, односно во синус. А аргументот тангента ја има формата
, тогаш името на функцијата мора да се смени во кофункција, односно во синус. А аргументот тангента ја има формата ![]() , затоа, името на функцијата треба да се остави исто.
, затоа, името на функцијата треба да се остави исто.
Како резултат на тоа имаме  И . Можете да ја погледнете табелата со формули за намалување за да бидете сигурни дека добиените резултати се точни.
И . Можете да ја погледнете табелата со формули за намалување за да бидете сигурни дека добиените резултати се точни.
Одговор:
 И .
И .
За да го консолидирате материјалот, размислете за решавање на пример со специфични агли.
Пример.
Користејќи мнемоничко правило, сведете ги на тригонометриски функции со остар агол.
Решение.
Прво, да го замислиме аголот од 777 степени во форма неопходна за примена на мнемоничкото правило. Ова може да се направи на два начина: или.
Оригиналниот агол е аголот на првата четвртина, синусот за овој агол има знак плус.
За да се претстави, името на синусот мора да се остави исто, но за да се претстави типот, синусот ќе треба да се смени во косинус.
Како резултат на тоа, имаме и .
Одговор:
![]() И .
И .
За да ја заклучите оваа точка, разгледајте пример кој ја илустрира важноста на правилното претставување на аголот под знакот на тригонометриските функции за примена на мнемоничкото правило: аголот мора да биде остар!!!
Да ја пресметаме тангентата на аголот. Во принцип, повикувајќи се на материјалот во написот вредности на синус, косинус, тангента и котангента, можеме веднаш да одговориме на прашањето за проблемот: ![]() .
.
Ако претставуваме агол како или како , тогаш можеме да го користиме мнемоничкото правило: ![]() И
И ![]() , што не води до истиот резултат.
, што не води до истиот резултат.
Но, ова е она што може да се случи ако земете претстава на агол, на пример, на формата. Во овој случај, мнемоничкото правило ќе не доведе до овој резултат. Овој резултат е неточен, а тоа се објаснува со фактот дека за претставата немавме право да го примениме мнемоничкото правило, бидејќи аголот не е остар.
Формули за доказ за намалување
Формулите за редукција ги рефлектираат својствата на периодичноста, симетријата и поместувањето по агли и . Веднаш да забележиме дека сите формули за намалување може да се докажат со отфрлање на терминот во аргументите, бидејќи тоа значи менување на аголот со цел број на целосни вртежи, а тоа не ги менува вредностите на тригонометриските функции. Овој термин служи како одраз на периодичноста.
Првиот блок од 16 формули за редукција следи директно од својствата на синус, косинус, тангента и котангента. Не вреди ни да се задржиме на нив.
Ајде да преминеме на следниот блок формули. Прво, да ги докажеме првите две од нив. Останатото следува од нив. Значи, да ги докажеме формулите за намалување на формата  И
И  .
.
Да го разгледаме кругот на единицата. Нека почетната точка А, по ротација за агол, оди во точката A 1 (x, y), а по ротација за агол, во точката A 2. Да нацртаме A 1 H 1 и A 2 H 2 – нормални на правата Ox.

Тоа е лесно да се види правоаголни триаголници OA 1 H 1 и OA 2 H 2 се еднакви во хипотенузата и два соседни агли. Од еднаквоста на триаголниците и локацијата на точките A 1 и A 2 на единица кругстанува јасно дека ако точката A 1 има координати x и y, тогаш точката A 2 има координати −y и x. Тогаш дефинициите за синус и косинус ни дозволуваат да ги напишеме еднаквостите и  , од што произлегува дека
, од што произлегува дека  И
И  . Ова ги докажува формулите за намалување што се разгледуваат за кој било агол.
. Ова ги докажува формулите за намалување што се разгледуваат за кој било агол.
Со оглед на тоа  И
И  (доколку е потребно, видете ја статијата основни тригонометриски идентитети), како и штотуку докажаните формули, ги добиваме и
(доколку е потребно, видете ја статијата основни тригонометриски идентитети), како и штотуку докажаните формули, ги добиваме и  . Така, ги докажавме следните две формули за намалување.
. Така, ги докажавме следните две формули за намалување.
За да се докажуваат формулите за редукција со аргумент, доволно е да се претстави како , а потоа да се користат докажаните формули и својства на тригонометриските функции со спротивни аргументи. На пример,.
Сите други формули за намалување се докажуваат слично врз основа на оние кои се веќе докажани со двојна примена. На пример, се појавува како ![]() , и - како
, и - како  . И и - како и соодветно.
. И и - како и соодветно.
Референци.
- Алгебра:Учебник за 9-то одделение. просечно училиште/Ју. Н. Макаричев, Н. Г. Миндјук, К. И. Нешков, С. Б. Суворова; Ед. S. A. Telyakovsky - М.: Образование, 1990. - 272 стр.: ISBN 5-09-002727
- Башмаков М.И.Алгебра и почетоците на анализата: Учебник. за 10-11 одделение. просечно училиште - 3-то издание. - М .: Образование, 1993. - 351 стр.: ill. - ISBN 5-09-004617-4.
- Алгебраи почеток на анализа: Проц. за 10-11 одделение. општо образование институции / A. N. Kolmogorov, A. M. Abramov, Yu P. Dudnitsyn и други; Ед. А. Н. Колмогоров - 14-то издание - М.: Образование, 2004. - 384 стр.
- Гусев В.А., Мордкович А.Г.Математика (прирачник за оние кои влегуваат во техничките училишта): Проц. додаток.- М.; Повисоко училиште, 1984.-351 стр., ил.
Формулите за редукција се односи што ви дозволуваат да одите од синус, косинус, тангента и котангента со аглите `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi) 2 \pm \alpha`, `2\pi \pm \alpha` на истите функции на аголот `\alpha`, кој се наоѓа во првата четвртина од единечниот круг. Така, формулите за намалување нè „водат“ да работиме со агли во опсег од 0 до 90 степени, што е многу погодно.
Сите заедно има 32 формули за намалување. Тие несомнено ќе ни се најдат за време на обединетиот државен испит, испитите и тестовите. Но, веднаш да ве предупредиме дека нема потреба да ги меморирате! Треба да потрошите малку време и да го разберете алгоритмот за нивна примена, тогаш нема да ви биде тешко вистински моментја изведуваат потребната еднаквост.
Прво, да ги запишеме сите формули за намалување:
За агол (`\frac (\pi)2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac (\pi)2 - \alpha)=cos \\alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 - \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
За агол (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi - \alpha)=sin \ \alpha;`` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
За агол (`\frac (3\pi)2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac (3\pi)2 — \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 — \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
За агол (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Често можете да најдете формули за намалување во форма на табела каде аглите се напишани во радијани:
За да го користите, треба да го изберете редот со функцијата што ни треба и колоната со потребниот аргумент. На пример, за да дознаете со помош на табела со што ќе биде еднакво `sin(\pi + \alpha)`, доволно е да го најдете одговорот на пресекот на редот `sin \beta` и колоната ` \pi + \алфа`. Добиваме `sin(\pi + \alpha)=-sin \ \alpha`.
И втората, слична табела, каде што аглите се напишани во степени:

Мнемоничко правило за формули за редукција или како да ги запомните
Како што веќе споменавме, нема потреба да се запаметат сите горенаведени врски. Ако ги погледнете внимателно, веројатно забележавте некои дезени. Тие ни овозможуваат да формулираме мнемоничко правило (мнемоничко - запомнете), со чија помош лесно можеме да добиеме каква било формула за намалување.
Веднаш да забележиме дека за да го примените ова правило, треба да бидете добри во идентификување (или запомнување) на знаците на тригонометриските функции во различни четвртини од единечниот круг.  Самата вакцина содржи 3 фази:
Самата вакцина содржи 3 фази:
- Аргументот на функцијата мора да биде претставен како `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha` и `\alpha` е потребно акутен агол(од 0 до 90 степени).
- За аргументи `\frac (\pi)2 \pm \alpha`, `\frac (3\pi)2 \pm \alpha` тригонометриска функцијаизразот што се претвора се менува во кофункција, односно спротивно (синус во косинус, тангента во котангенс и обратно). За аргументите `\pi \pm \alpha`, `2\pi \pm \alpha` функцијата не се менува.
- Се одредува знакот на оригиналната функција. Резултирачката функција на десната страна ќе го има истиот знак.
За да видиме како ова правило може да се примени во пракса, ајде да трансформираме неколку изрази:
1. `cos(\pi + \alpha)`.
Функцијата не е обратна. Аголот `\pi + \alpha` е во третата четвртина, косинусот во оваа четвртина има знак „-“, така што трансформираната функција ќе има и знак „-“.
Одговор: ` cos(\pi + \alpha)= - cos \alpha`
2. `sin(\frac (3\pi)2 - \алфа)`.
Според мнемоничкото правило, функцијата ќе биде обратна. Аголот `\frac (3\pi)2 - \alpha` е во третата четвртина, синусот овде има знак „-“, така што резултатот ќе има и знак „-“.
Одговор: `sin(\frac (3\pi)2 - \alpha)= - cos \alpha`
3. `cos(\frac (7\pi)2 - \alpha)`.
`cos(\frac (7\pi)2 - \alpha)=cos(\frac (6\pi)2+\frac (\pi)2-\alpha)=cos (3\pi+(\frac(\pi )2-\алфа))`. Да го претставиме `3\pi` како `2\pi+\pi`. `2\pi` е периодот на функцијата.
Важно: Функциите `cos \alpha` и `sin \alpha` имаат период од `2\pi` или `360^\circ`, нивните вредности нема да се променат ако аргументот се зголеми или намали за овие вредности.
Врз основа на ова, нашиот израз може да се напише на следниов начин: `cos (\pi+(\frac(\pi)2-\alpha)`. Применувајќи го мнемоничкото правило двапати, добиваме: `cos (\pi+(\frac(\ pi) 2-\alpha)= - cos (\frac(\pi)2-\alpha)= - sin \alpha`.
Одговор: `cos(\frac (7\pi)2 - \alpha)=- sin \alpha`.
Правило за коњи
Втората точка од мнемоничкото правило опишано погоре се нарекува и коњско правило на формули за редукција. Се прашувам зошто коњи?
Значи, имаме функции со аргументи `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, точките `\frac (\pi)2`, `\pi`, `\frac (3\pi)2`, `2\pi` се клучни, тие се наоѓаат на координатните оски. `\pi` и `2\pi` се на хоризонталната x-оска, а `\frac (\pi)2` и `\frac (3\pi)2` се на вертикалната ордината.
Си го поставуваме прашањето: „Дали функцијата се менува во кофункција? За да одговорите на ова прашање, треба да ја движите главата по оската на која се наоѓа клучната точка.
Тоа е, за аргументи со клучни точки лоцирани на хоризонталната оска, ние одговараме „не“ со тресење на главите на страните. А за аглите со клучни точки лоцирани на вертикалната оска, одговараме „да“ со климање со главата од горе до долу, како коњ :)
Препорачуваме да гледате видео туторијал во кој авторот детално објаснува како да запомните формули за намалување без да ги меморирате.
Практични примери за користење на формули за редукција
Употребата на формули за намалување започнува во 9 и 10 одделение. Многу проблеми со нивното користење беа доставени на Единствениот државен испит. Еве некои од проблемите каде што ќе треба да ги примените овие формули:
- проблеми за решавање правоаголен триаголник;
- нумерички и азбучни конверзии тригонометриски изрази, пресметка на нивните вредности;
- стереометриски задачи.
Пример 1. Пресметајте користејќи формули за редукција а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`.
Решение: а) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;
б) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac(\sqrt 3)3`;
в) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac(\sqrt 3)2`;
г) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac(\sqrt 3)2`.
Пример 2. Имајќи изразено косинус преку синус користејќи формули за редукција, споредете ги броевите: 1) `sin \frac (9\pi)8` и `cos \frac (9\pi)8`; 2) `sin \frac (\pi)8` и `cos \frac (3\pi)10`.
Решение: 1)`sin \frac (9\pi)8=sin (\pi+\frac (\pi)8)=-sin \frac (\pi)8`
`cos \frac (9\pi)8=cos (\pi+\frac (\pi)8)=-cos \frac (\pi)8=-sin \frac (3\pi)8`
`-sin \frac (\pi)8> -sin \frac (3\pi)8`
`sin \frac (9\pi)8>cos \frac (9\pi)8`.
2) `cos \frac (3\pi)10=cos (\frac (\pi)2-\frac (\pi)5)=sin \frac (\pi)5`
`sin \frac (\pi)8 `sin \frac (\pi)8 Прво да докажеме две формули за синусот и косинусот на аргументот `\frac (\pi)2 + \alpha`: ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha` и ` cos (\frac (\ pi)2 + \alpha)=-sin \\alpha`. Останатите се изведени од нив. Да земеме единечна кружница и да ја точкаме А на неа со координати (1,0). Нека откако ќе се свртиме кон Доаѓајќи од дефиницијата за тангента и котангента, добиваме ` tan(\frac (\pi)2 + \alpha)=\frac (sin(\frac (\pi)2 + \alpha))(cos(\frac (\ pi)2 + \alpha))=\frac (cos \alpha)(-sin \alpha)=-ctg \alpha` и ` сtg(\frac (\pi)2 + \alpha)=\frac (cos(\ frac (\ pi)2 + \alpha))(sin(\frac (\pi)2 + \alpha))=\frac (-sin \alpha)(cos \alpha)=-tg \alpha`, што го докажува формули за редукција за тангента и котангента на аголот `\frac (\pi)2 + \alpha`. За да се докажуваат формули со аргументот `\frac (\pi)2 - \alpha`, доволно е да се претстави како `\frac (\pi)2 + (-\alpha)` и да се следи истата патека како погоре. На пример, `cos(\frac (\pi)2 - \alpha)=cos(\frac (\pi)2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`. Аглите `\pi + \alpha` и `\pi - \alpha` може да се претстават како `\frac (\pi)2 +(\frac (\pi)2+\alpha)` и `\frac (\pi ) 2 +(\frac (\pi)2-\алфа)` соодветно. И `\frac (3\pi)2 + \alpha` и `\frac (3\pi)2 - \alpha` како `\pi +(\frac (\pi)2+\alpha)` и `\pi +(\frac (\pi)2-\алфа)`. Како да запомните формули за намалување на тригонометриските функции? Лесно е ако користите асоцијација Оваа асоцијација не е измислена од мене. Како што веќе споменавме, добрата асоцијација треба да „фати“, односно да предизвикува живи емоции. Емоциите предизвикани од оваа асоцијација не можам да ги наречам позитивни. Но, тоа дава резултат - ви овозможува да ги запомните формулите за намалување, што значи дека има право да постои. На крајот на краиштата, ако не ви се допаѓа, не мора да го користите, нели? Формулите за редукција имаат форма: sin(πn/2±α), cos(πn/2±α), tg(πn/2±α), ctg(πn/2±α). Запомнете дека +α дава движење спротивно од стрелките на часовникот, - α дава движење во насока на стрелките на часовникот. За да работите со формули за намалување, потребни ви се две точки: 1) стави го знакот што го има почетната функција (во учебниците пишуваат: сведува. Но за да не се збуни подобро е да се нарече почетен), ако за α се смета аголот на првата четвртина т.е. , мал. 2) Хоризонтален дијаметар - π±α, 2π±α, 3π±α... - генерално, кога нема дропка, името на функцијата не се менува. Вертикална π/2±α, 3π/2±α, 5π/2±α... - кога има дропка името на функцијата се менува: синус - во косинус, косинус - во синус, тангента - во котангента и котангента - до тангента. Сега, всушност, здружението: вертикален дијаметар (има фракција) - стоејќи пијан. Што ќе се случи со него рано? или предоцна е? Така е, ќе падне. Името на функцијата ќе се промени. Ако дијаметарот е хоризонтален, пијаниот веќе лежи. Веројатно спие. Ништо нема да му се случи, тој веќе зазеде хоризонтална положба. Според тоа, името на функцијата не се менува. Односно sin(π/2±α), sin(3π/2±α), sin(5π/2±α) итн. дадете ±cosα, и грев (π±α), грев (2π±α), грев (3π±α), ... - ±sinα. Веќе знаеме како. Како функционира ова? Ајде да погледнеме примери. 1) cos(π/2+α)=? Стануваме π/2. Бидејќи +α значи дека одиме напред, спротивно од стрелките на часовникот. Се наоѓаме во втората четвртина, каде што косинусот има знак „-“. Името на функцијата се менува („стои пијан“, што значи дека ќе падне). Значи, cos(π/2+α)=-sin α. Да дојдеме до 2π. Бидејќи -α - одиме наназад, односно во насока на стрелките на часовникот. Се наоѓаме во IV четвртина, каде што тангентата има знак „-“. Името на функцијата не се менува (дијаметарот е хоризонтален, „пијаниот веќе лежи“). Така, tan(2π-α)=- tanα. 3) ctg²(3π/2-α)=? Примерите во кои функцијата е подигната на рамномерна моќност се уште поедноставни за решавање. Парниот степен „-“ го отстранува, односно само треба да откриете дали името на функцијата се менува или останува. Дијаметарот е вертикален (има фракција, „стои пијан“, ќе падне), името на функцијата се менува. Добиваме: ctg²(3π/2-α)= tan²α. Дефиниција.
Формулите за редукција се формули кои ви дозволуваат да преминете од тригонометриски функции на формата до функции на аргумент. Со нивна помош, синусот, косинус, тангента и котангента на произволен агол може да се сведе на синус, косинус, тангента и котангента на агол од интервалот од 0 до 90 степени (од 0 до радијани). Така, формулите за намалување ни овозможуваат да продолжиме да работиме со агли од 90 степени, што несомнено е многу погодно. Формули за намалување: Постојат две правила за користење на формули за намалување.
1.
Ако аголот може да се претстави како (π/2 ±a) или (3*π/2 ±a), тогаш се менува името на функцијатагрев на кос, кос на грев, тг до цтг, цтг до тг. Ако аголот може да се претстави во форма (π ±a) или (2*π ±a), тогаш Името на функцијата останува непроменето. Погледнете ја сликата подолу, таа шематски покажува кога да го смените знакот, а кога не 2. Знак за намалена функција
останува иста. Ако оригиналната функција имала знак плус, тогаш намалената функција има и знак плус. Ако оригиналната функција имала знак минус, тогаш намалената функција има и знак минус. На сликата подолу се прикажани знаците на основните тригонометриски функции во зависност од четвртината. Пример:
Пресметај Ајде да ги користиме формулите за намалување: Sin(150˚) е во втората четвртина од сликата гледаме дека знакот за грев во оваа четвртина е еднаков на „+“. Ова значи дека дадената функција ќе има и знак „+“. Го применивме второто правило. Сега 150˚ = 90˚ +60˚. 90˚ е π/2. Односно, имаме работа со случајот π/2+60, затоа, според првото правило, функцијата ја менуваме од sin во cos. Како резултат на тоа, добиваме Sin(150˚) = cos(60˚) = ½. Тие припаѓаат на тригонометрискиот дел од математиката. Нивната суштина е да се намалат тригонометриските функции на аглите во „едноставна“ форма. Може многу да се напише за важноста да се познаваат. Веќе има 32 од овие формули! Не плашете се, не треба да ги учите, како и многу други формули на курсот по математика. Нема потреба да ја полните главата со непотребни информации, треба да ги запомните „клучевите“ или законите, а запомнувањето или изведувањето на потребната формула нема да биде проблем. Патем, кога пишувам во статии „... треба да научиш!!!“ - тоа значи дека навистина треба да се научи. Ако не сте запознаени со формулите за намалување, тогаш едноставноста на нивното изведување пријатно ќе ве изненади - постои „закон“ со помош на кој тоа може лесно да се направи. И можете да напишете која било од 32-те формули за 5 секунди. Ќе наведам само дел од проблемите што ќе се појават на Единствениот државен испит по математика, каде што без познавање на овие формули постои голема веројатност да не успее да ги реши. На пример: – проблеми за решавање правоаголен триаголник, каде што зборуваме за надворешниот агол, и проблеми за внатрешните агли, некои од овие формули се исто така неопходни. – задачи за пресметување на вредностите на тригонометриските изрази; конвертирање на нумерички тригонометриски изрази; конвертирање на буквални тригонометриски изрази. – проблеми за тангентата и геометриското значење на тангентата е потребна редуцирачка формула за тангентата, како и други проблеми; – стереометриски проблеми, во текот на решавањето често е потребно да се определи синус или косинус на агол кој се наоѓа во опсег од 90 до 180 степени. И ова се само оние точки кои се однесуваат на Единствениот државен испит. И во самиот курс на алгебра има многу проблеми, чиешто решение едноставно не може да се направи без познавање на формулите за намалување. Значи, до што води ова и како наведените формули ни го олеснуваат решавањето на проблемите? На пример, треба да одредите синус, косинус, тангента или котангента на кој било агол од 0 до 450 степени: аголот на алфа се движи од 0 до 90 степени * * *
Значи, неопходно е да се разбере „законот“ што функционира овде: 1. Определи го знакот на функцијата во соодветниот квадрант. Да те потсетам: 2. Запомнете го следново: функцијата се менува во кофункција
функцијата не се менува во кофункција
Што значи концептот - функцијата се менува во кофункција?
Одговор: синусот се менува во косинус или обратно, тангента на котангента или обратно.
Тоа е тоа! Сега, според презентираниот закон, самите ќе напишеме неколку формули за намалување: Овој агол лежи во третата четвртина, косинусот во третата четвртина е негативен. Не ја менуваме функцијата во кофункција, бидејќи имаме 180 степени, што значи: Аголот лежи во првата четвртина, синусот во првата четвртина е позитивен. Не ја менуваме функцијата во кофункција, бидејќи имаме 360 степени, што значи: Еве уште една потврда дека синусите на соседните агли се еднакви: Аголот лежи во втората четвртина, синусот во втората четвртина е позитивен. Не ја менуваме функцијата во кофункција, бидејќи имаме 180 степени, што значи: Работете ја секоја формула ментално или писмено и ќе се уверите дека нема ништо комплицирано. ***
Во написот за решението, беше забележан следниов факт - синусот на еден остар агол во правоаголен триаголник е еднаков на косинус на друг остар агол во него. агол `\alpha` ќе оди во точката `A_1(x, y)`, а по вртење по агол `\frac (\pi)2 + \alpha` во точката `A_2(-y, x)`. Спуштајќи ги перпендикуларите од овие точки на правата OX, гледаме дека триаголниците `OA_1H_1` и `OA_2H_2` се еднакви, бидејќи нивните хипотенуси и соседните агли се еднакви. Потоа, врз основа на дефинициите за синус и косинус, можеме да напишеме `sin\alpha=y`, `cos\alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\ pi)2 + \алфа)=-y`. Каде можеме да напишеме дека ` sin(\frac (\pi)2 + \alpha)=cos \alpha` и `cos(\frac (\pi)2 + \alpha)=-sin \alpha`, што го докажува намалувањето формули за синусни и косинусни агли `\frac (\pi)2 + \alpha`.
агол `\alpha` ќе оди во точката `A_1(x, y)`, а по вртење по агол `\frac (\pi)2 + \alpha` во точката `A_2(-y, x)`. Спуштајќи ги перпендикуларите од овие точки на правата OX, гледаме дека триаголниците `OA_1H_1` и `OA_2H_2` се еднакви, бидејќи нивните хипотенуси и соседните агли се еднакви. Потоа, врз основа на дефинициите за синус и косинус, можеме да напишеме `sin\alpha=y`, `cos\alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\ pi)2 + \алфа)=-y`. Каде можеме да напишеме дека ` sin(\frac (\pi)2 + \alpha)=cos \alpha` и `cos(\frac (\pi)2 + \alpha)=-sin \alpha`, што го докажува намалувањето формули за синусни и косинусни агли `\frac (\pi)2 + \alpha`.