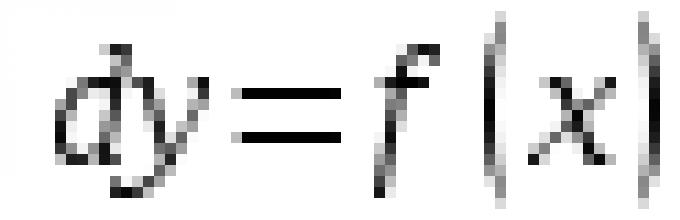За страницата
Неопределен интеграл
1Антидериватив и неопределен интеграл 1
2Наједноставните својства на неопределен интеграл. 3
Табела со основни интеграли 3
2.1 Дополнителна табела на интеграли 4
3 Замена на променлива во неопределен интеграл 5
3.1 Начин на интегрирање на функции од формата и (a≠ 0). 6
4 Интеграција по делови во неопределен интеграл 7
4.1Метод на интегрирање на функциите на формата. 7
4.2 Начин на интегрирање на функции од формата: 8
5 Интеграција на рационални дропки 8
5.1Метод на интегрирање на едноставни дропки од тип 4. 11
6Интеграција на ирационални изрази 12
6.1Интеграција на тригонометриски изрази 14
Антидериватив и неопределен интеграл
Решавање на диференцијалната равенка
![]()
на интервалот, т.е. наоѓаме функција таква што . Бидејќи , тогаш равенката (1) може да се препише во диференцијали:Секое решение за таква равенка се нарекува антидериват на функцијата. Значи функцијата се нарекуваантидеривативна функција
на интервалот, ако за сите. Случаите и/или не се исклучени. Јасно е дека ако е антидеривативно, тогаш е и антидеривативно. Наша задача е да ги најдеме сите решенија на равенката (1). Функција од две променливи се нарекува општо решение на равенката (1) или, со други зборови,
неопределен интегралфункција ако, при замена наместо кој било број, добиеме одредено решение на равенката (1) и секое конкретно решение на равенката (1) се добива на овој начин.
Неопределениот интеграл се означува со .
Функцијата се нарекува интегранд, диференцијалот се нарекува интегранд, а знакот на интегралот (растегната латинска буква S, првата буква од зборот Sum е сума). Се поставува прашањето за постоењето на антидериват и неопределен интеграл. Во делот „Дефинитивен интеграл“, § Њутн-Лајбницова формула, ќе се докаже дека антидериватот на континуирана функција секогаш постои. Лема.
Нека биде идентично за сите. Тогаш е константа на овој интервал. ![]() Доказ. Дозволете ни да означиме за која било точка. Да земеме произволна точка и да ја примениме теоремата на Лагранж на разликата: за одредена точка . Ова ја докажува лемата.□
Доказ. Дозволете ни да означиме за која било точка. Да земеме произволна точка и да ја примениме теоремата на Лагранж на разликата: за одредена точка . Ова ја докажува лемата.□ ![]() .
□
.
□
Теорема за антидеривати. Два антидеривати со иста функција дефинирани на интервал се разликуваат по константа. ![]() .
.
Забележете дека ако не земеме интервал како функција ODZ, туку, на пример, такво исклучено множество како спој на два интервали ![]() , Тоа
која било функција на формата
, Тоа
која било функција на формата
![]()
има нула дериват, и на тој начин лемата и теоремата за антидеривати престануваат да бидат вистинити во овој случај.
Наједноставните својства на неопределен интеграл.
1. Интегралот на збирот е еднаков на збирот на интегралите:
2. Константата може да се извади од интегралниот знак:
3. Изводот на интегралот е еднаков на интегранд функцијата.
4. Диференцијалот на интегралот е еднаков на интеграндскиот израз.
5. (Линеарна промена на променливите) Ако ![]() , Тоа
, Тоа ![]() (Тука).
(Тука).
Табела на основни интеграли
![]()
Конкретно,
За исклучителен случај имаме:
![]()

![]()
Дополнителна табела на интеграли
![]()
![]()
Промена на променлива во неопределен интеграл
Да ја прошириме дефиницијата за неопределен интеграл на поопшт случај: претпоставуваме по дефиниција. Така, на пример
Теорема.Нека е диференцијабилна функција. Потоа
Доказ. Нека ![]() . Потоа
. Потоа
што требаше да се докаже.□
Во посебниот случај кога добиваме линеарна промена на променливите (види Својство 5, §1). Примената на формулата (1) „од лево кон десно“ ќе значи замена на променлива. Примената на формулата (1) во спротивна насока, „од десно кон лево“, се нарекува внесување под диференцијалниот знак.
Примери.А.

1. Изберете го изводот на квадратниот трином во броителот:
3. За да го пресметаме првиот интеграл во (2), го користиме записот под диференцијалниот знак:
За да го пресметаме вториот интеграл, избираме целосен квадрат во квадратниот трином и го намалуваме на табеларен со линеарна промена на променливите.
Истиот метод се користи за пресметување на интеграли на формата ![]()
Примери
Интеграција по делови во неопределен интеграл
Теорема.За диференцијабилни функции и релацијата важи
Доказ. Интегрирање на левата и десната страна на формулата ![]() , добиваме:
, добиваме:
Бидејќи по дефиниција и , следува формулата (1).□
Пример.
За да интегрираме такви функции, го внесуваме полиномот под диференцијалниот знак и ја применуваме формулата за интеграција по делови. Постапката ја повторуваме k пати.
Пример.

Интегрирање на рационални дропки
Рационална дропкасе нарекува функција од формата , каде што се полиноми. Ако , тогаш се нарекува рационалната дропка точно. Инаку се вика погрешно.
Следниве рационални дропки се нарекуваат наједноставни
(тип 2) ![]()
(тип 3) ![]()
(тип 4) ![]() ,
,
Теорема 1.Секоја дропка може да се прошири во збир на полином и правилна рационална дропка.
Доказ. Нека е неправилна рационална дропка. Ајде да го поделиме броителот со именителот со остаток: Еве полиноми, а потоа
Дропката е точна поради неравенството. □
Теорема 2.Секоја соодветна рационална дропка може да се разложи на едноставна сума.
Алгоритам за распаѓање.
а) Именителот на соодветната дропка го прошируваме во производ на нередуцирани полиноми (линеарни и квадратни со негативна дискриминантна):
Еве ![]() и -- мноштвото на соодветните корени.
и -- мноштвото на соодветните корени.
б) Дропката ја прошируваме во збир од наједноставните со неодредени коефициенти според следниве принципи:
Ова го правиме за секој линеарен фактор и за секој квадратен фактор.
в) Добиеното проширување го множиме со заеднички именител и ги наоѓаме неодредените коефициенти од условот левата и десната страна да се идентични. Ние користиме комбинација од два методи
??? – образложение за алгоритмот
Примери.А. Ајде да се прошириме ![]() до збир од наједноставните
до збир од наједноставните
Следи дека. Заменувајќи го овој сооднос веднаш наоѓаме . Значи
B. Да ја прошириме рационалната дропка ![]() до збир од наједноставните. Проширувањето на оваа дропка со неодредени коефициенти ја има формата
до збир од наједноставните. Проширувањето на оваа дропка со неодредени коефициенти ја има формата ![]()
Со множење со заеднички именител ја добиваме релацијата
Заменувајќи овде, откриваме од каде потекнува. Замена наоѓаме ![]() .
.

Изедначувајќи ги коефициентите за го добиваме системот ![]() Оттука и. Со собирање на еднаквостите на последниот систем, добиваме и . Потоа
Оттука и. Со собирање на еднаквостите на последниот систем, добиваме и . Потоа

И

Оттука,/**/ Задача.
![]()
Генерализирајте го резултатот од примерот А и докажете ја еднаквоста
Метод за интегрирање на едноставни дропки од тип 4. ![]() а) Изолирајќи го изводот на именителот во броителот, го прошируваме интегралот
а) Изолирајќи го изводот на именителот во броителот, го прошируваме интегралот
во збир од два интеграли.
б) Првиот од добиените интеграли, откако ќе се внесе под диференцијалниот знак, ќе стане табеларен.

в) Во вториот, избираме целосен квадрат во именителот и ја намалуваме пресметката на интеграл од формата. На овој интеграл ја применуваме следната повторлива процедура
До последниот интеграл ја применуваме формулата за интеграција по делови: ![]() Значи, ако дефинираме
Значи, ако дефинираме
, Тоа ![]() .
.
Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност
Пример
Интегрирање на ирационални изрази ![]() Интеграли на формата
Интеграли на формата
, каде m/n,...,r/s се рационални броеви со заеднички именител k, се сведуваат на интеграл на рационална функција со замена
![]()
Тогаш тие се рационални изрази, затоа, по замената, се добива интегралот на рационалната дропка:
Откако го пресметавме овој интеграл (види пар. 4) и направивме обратна замена, го добиваме одговорот.
![]()
Слично, интеграли на формата
Примерикаде ad-bc≠ 0, и k го има истото значење како погоре, се сведуваат на интеграли на рационалната дропка со замена
. А. Да го пресметаме интегралот
B. Пресметај го интегралот
Поедноставен метод за интегрирање (но бара претпоставка) истата функција е:
Интегрирање на ирационални изрази ![]() се сведуваат на интеграли на рационална функција со универзална замена
се сведуваат на интеграли на рационална функција со универзална замена
![]()


затоа интегралот го добиваме од рационалниот израз
Во посебни случаи R(sin x) cos x dx, R(cos x) sin x dx и R(sin 2 x, cos 2 x, tan x, ctg x) dx подобро е соодветно да се користат замени.
>> Методи на интеграција
Основни методи на интеграција
Дефиниција на интеграл, определен и неопределен интеграл, табела на интеграли, Њутн-Лајбницова формула, интеграција по делови, примери за пресметување интеграли.
Неопределен интеграл
Се повикува функцијата F(x) што може да се диференцира во даден интервал X антидериват на функцијата f(x), или интегралот на f(x), ако за секој x ∈X важи следнава еднаквост:
F "(x) = f(x). (8.1)
Наоѓањето на сите антидеривати за дадена функција се нарекува нејзино интеграција. Неопределена интегрална функција f(x) на даден интервал X е множество од сите антидеривативни функции за функцијата f(x); ознака -
Ако F(x) е некој антидериват за функцијата f(x), тогаш ∫ f(x)dx = F(x) + C, (8.2)
каде што C е произволна константа.
Табела на интеграли
Директно од дефиницијата ги добиваме главните својства на неопределен интеграл и список на табеларни интеграли:
1) d∫f(x)dx=f(x)
2)∫df(x)=f(x)+C
3) ∫af(x)dx=a∫f(x)dx (a=const)
4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx
Список на интеграли на табелата
1. ∫x m dx = x m+1 /(m + 1) +C; (m ≠ -1)
3.∫a x dx = a x /ln a + C (a>0, a ≠1)
4.∫e x dx = e x + C
5.∫sin x dx = cosx + C
6.∫cos x dx = - sin x + C
7. = арктан x + C
8. = arcsin x + C
10. = - ctg x + C
Замена на променлива
За да интегрирате многу функции, користете го методот за замена на променлива или замени,што ви овозможува да ги намалите интегралите во табеларна форма.
Ако функцијата f(z) е континуирана на [α,β], функцијата z =g(x) има континуиран извод и α ≤ g(x) ≤ β, тогаш
∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)
Притоа, по интеграцијата на десната страна, треба да се направи замена z=g(x).
За да се докаже тоа, доволно е да се напише оригиналниот интеграл во форма:
∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).
На пример:
1) 

2)  .
.
Начин на интеграција по делови
Нека u = f(x) и v = g(x) се функции кои имаат континуирано . Потоа, според работата,
d(uv))= udv + vdu или udv = d(uv) - вду.
За изразот d(uv), антидериватот очигледно ќе биде uv, така што формулата важи:
∫ udv = uv - ∫ vdu (8.4.)
Оваа формула го изразува правилото интеграција по делови. Тоа ја води интеграцијата на изразот udv=uv"dx до интегрирање на изразот vdu=vu"dx.
Нека, на пример, сакате да најдете ∫xcosx dx. Да ставиме u = x, dv = cosxdx, па du=dx, v=sinx. Потоа
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Правилото за интеграција по делови има поограничен опсег од замена на променливи. Но, постојат цели класи на интеграли, на пример,
∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и други, кои се пресметуваат прецизно користејќи интеграција по делови.
Дефинитивен интеграл
Концептот на дефинитивен интеграл е воведен на следниов начин. Нека е дефинирана функција f(x) на интервал. Да ја поделиме отсечката [a,b] на nделови по точки a= x 0< x 1 <...< x n = b. Из каждого интервала (x i-1 ,
x i) возьмем произвольную точку ξ i и составим сумму f(ξ i)
Δx i где
Δ x i =x i - x i-1. Се вика збир од формата f(ξ i)Δ x i интегрален збир, а неговата граница на λ = maxΔx i → 0, ако постои и е конечна, се вика определен интегралфункции f(x) на адо би е назначен:
F(ξ i)Δx i (8.5).
Функцијата f(x) во овој случај се повикува интеграбилна на интервалот, се повикуваат броевите a и b долните и горните граници на интегралот.
Следниве својства се точни за дефинитивен интеграл:
4), (k = const, k∈R);
5)![]()
6)![]()
7) f(ξ)(b-a) (ξ∈).
Последниот имот се нарекува теорема за средна вредност.
Нека f(x) е континуиран на . Тогаш на оваа отсечка има неопределен интеграл
∫f(x)dx = F(x) + C
и се одвива Формула Њутн-Лајбниц, поврзувајќи го определениот интеграл со неопределениот интеграл:
F(b) - F(a). (8.6)
Геометриска интерпретација: дефинитивниот интеграл е плоштината на криволинеарен трапез ограничен одозгора со кривата y=f(x), правите x = a и x = b и отсечка од оската Вол.
Несоодветни интеграли
Интеграли со бесконечни граници и интеграли на дисконтинуирани (неограничени) функции се нарекуваат не свој. Неправилни интеграли од прв вид -Овие се интеграли во бесконечен интервал, дефинирани на следниов начин:
![]() (8.7)
(8.7)
Ако оваа граница постои и е конечна, тогаш се нарекува конвергентен неправилен интеграл на f(x)на интервалот [a,+ ∞), и се повикува функцијата f(x). интеграбилна во бесконечен интервал[a,+ ∞). Инаку, интегралот се вели дека е не постои или се разминува.
Неправилните интеграли на интервалите (-∞,b] и (-∞, + ∞) се дефинирани слично:


Дозволете ни да го дефинираме концептот на интеграл на неограничена функција. Ако f(x) е континуиран за сите вредности xотсечка , освен точката c, во која f(x) има бесконечен дисконтинуитет, тогаш неправилен интеграл од вториот вид на f(x) кои се движат од а до бизносот се вика:
![]()
ако овие граници постојат и се конечни. Ознака:
Примери на интегрални пресметки
Пример 3.30.Пресметај ∫dx/(x+2).
Решение.Да означиме t = x+2, потоа dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.
Пример 3.31. Најдете ∫ tgxdx.
Решение.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. Нека t=cosx, тогаш ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.
Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност3.32 . Најдете ∫dx/sinxРешение.



Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност3.33. Најдете .
Решение. =

 .
.
Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност3.34 . Најдете ∫arctgxdx.
Решение. Ајде да се интегрираме по делови. Да означиме u=arctgx, dv=dx. Тогаш du = dx/(x 2 +1), v=x, од каде ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; бидејќи
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.
Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност3.35 . Пресметај ∫lnxdx.
Решение.Применувајќи ја формулата за интеграција по делови, добиваме:
u=lnx, dv=dx, du=1/x dx, v=x. Тогаш ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.
Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност3.36 . Пресметај ∫e x sinxdx.
Решение.Да означиме u = e x, dv = sinxdx, потоа du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx. Интегралот ∫e x cosxdx го интегрираме и по делови: u = e x, dv = cosxdx, du=e x dx, v=sinx. Имаме:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Ја добивме релацијата ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx, од која 2∫e x sinx dx = - e x cosx + e x sinx + C.
Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност 3.37. Пресметај J = ∫cos(lnx)dx/x.
Решение.Бидејќи dx/x = dlnx, тогаш J= ∫cos(lnx)d(lnx). Заменувајќи го lnx преку t, доаѓаме до табелата интеграл J = ∫ costdt = sint + C = sin(lnx) + C.
Ова е рекурентна формула за пресметување на интегралите земајќи ја предвид почетната вредност 3.38 . Пресметај J = .
Решение.Со оглед на тоа = d(lnx), ја правиме замената lnx = t. Тогаш J = ![]() .
.
Интеграција по делови. Примери на решенија
Здраво повторно. Денес во лекцијата ќе научиме како да се интегрираме по делови. Методот на интеграција по делови е еден од темелите на интегралното сметање. За време на тестовите или испитите, од студентите речиси секогаш се бара да ги решат следниве видови интеграли: наједноставниот интеграл (види статија)или интеграл со замена на променлива (види статија)или интегралот е само вклучен метод на интеграција со делови.
Како и секогаш, треба да имате при рака: Табела на интегралиИ Табела со деривати. Ако сè уште ги немате, тогаш посетете ја просторијата за складирање на мојата веб-страница: Математички формули и табели. Нема да се уморам да повторувам - подобро е да испечатите сè. Ќе се обидам да го претставам целиот материјал доследно, едноставно и јасно. нема посебни потешкотии во интегрирањето на деловите.
Каков проблем решава методот на интеграција по делови? Начинот на интеграција по делови решава многу важен проблем, тој ви овозможува да интегрирате некои функции што не се во табелата; работафункции, а во некои случаи дури и количници. Како што се сеќаваме, не постои погодна формула: ![]() . Но, постои овој:
. Но, постои овој: ![]() – формула за интеграција по делови лично. Знам, знам, ти си единствениот - ќе работиме со неа во текот на целата лекција (сега е полесно).
– формула за интеграција по делови лично. Знам, знам, ти си единствениот - ќе работиме со неа во текот на целата лекција (сега е полесно).
И веднаш списокот во студио. Интегралите од следниве типови се земени по делови:
1) , ![]() , – логаритам, логаритам помножен со некој полином.
, – логаритам, логаритам помножен со некој полином.
2) ,![]() е експоненцијална функција помножена со некој полином. Ова исто така вклучува интеграли како - експоненцијална функција помножена со полином, но во пракса ова е 97 проценти, под интегралот има убава буква „е“. ... написот испаѓа донекаде лирски, о да ... дојде пролетта.
е експоненцијална функција помножена со некој полином. Ова исто така вклучува интеграли како - експоненцијална функција помножена со полином, но во пракса ова е 97 проценти, под интегралот има убава буква „е“. ... написот испаѓа донекаде лирски, о да ... дојде пролетта.
3) , ![]() , се тригонометриски функции помножени со некој полином.
, се тригонометриски функции помножени со некој полином.
4) , – инверзни тригонометриски функции („лакови“), „лакови“ помножени со некој полином.
Некои дропки се исто така земени во делови, ние исто така ќе ги разгледаме соодветните примери.
Интеграли на логаритми
Пример 1
Класичен. Од време на време овој интеграл може да се најде во табелите, но не е препорачливо да се користи готов одговор, бидејќи наставникот има пролетен недостаток на витамин и ќе пцуе многу. Бидејќи интегралот што се разгледува во никој случај не е табеларен - тој се зема во делови. Ние одлучуваме:
Го прекинуваме решението за меѓуобјаснувања.
Ја користиме формулата за интеграција по делови: ![]()
Формулата се применува од лево кон десно
Гледаме на левата страна: . Очигледно, во нашиот пример (и во сите други што ќе ги разгледаме), нешто треба да се означи како , и нешто како .
Во интегралите од типот што се разгледува, логаритамот секогаш се означува.
Технички, дизајнот на решението се спроведува на следниов начин:
Односно, логаритамот го означивме со, и со - остатокотинтегранд израз.
Следна фаза: најдете го диференцијалот:

Диференцијалот е скоро ист како изводот, веќе разговаравме како да го најдеме во претходните лекции.
Сега ја наоѓаме функцијата. За да ја пронајдете функцијата што треба да ја интегрирате десна странапомала еднаквост:

Сега го отвораме нашето решение и ја конструираме десната страна на формулата: .
Патем, еве примерок од конечното решение со неколку забелешки:

Единствената поента во работата е што веднаш го заменив и , бидејќи е вообичаено да се пишува факторот пред логаритамот.
Како што можете да видите, примената на формулата за интеграција по делови во суштина го намали нашето решение на два едноставни интеграли.
Ве молиме имајте предвид дека во некои случаи веднаш потоапримена на формулата, нужно се врши поедноставување под преостанатиот интеграл - во примерот што се разгледува, интеградот го сведевме на „x“.
Ајде да провериме. За да го направите ова, треба да го земете дериватот на одговорот:
Добиена е оригиналната интегранд функција, што значи дека интегралот е правилно решен.
За време на тестот, го користевме правилото за диференцијација на производот: ![]() . И ова не е случајно.
. И ова не е случајно.
Формула за интеграција по делови ![]() и формула
и формула ![]() – ова се две меѓусебно инверзни правила.
– ова се две меѓусебно инверзни правила.
Пример 2
Најдете го неопределен интеграл.
Интеграндот е производ на логаритам и полином.
Ајде да одлучиме.
![]()
Уште еднаш детално ќе ја опишам постапката за примена на правилото во иднина, примери ќе бидат претставени пократко, а доколку имате потешкотии да го решите сами, треба да се вратите на првите два примери од лекцијата; .
Како што веќе споменавме, неопходно е да се означи логаритамот (фактот дека е моќност не е важно). Означуваме со остатокотинтегранд израз.
Во колоната пишуваме:
Прво го наоѓаме диференцијалот:

Овде го користиме правилото за диференцијација на сложена функција ![]() . Не случајно на првата лекција од темата Неопределен интеграл. Примери на решенијаСе фокусирав на фактот дека за да се совладаат интегралите, неопходно е да се „добијат“ дериватите. Ќе треба да се занимавате со деривати повеќе од еднаш.
. Не случајно на првата лекција од темата Неопределен интеграл. Примери на решенијаСе фокусирав на фактот дека за да се совладаат интегралите, неопходно е да се „добијат“ дериватите. Ќе треба да се занимавате со деривати повеќе од еднаш.
Сега ја наоѓаме функцијата, за ова се интегрираме десна странапомала еднаквост:

За интеграција ја користевме наједноставната табеларна формула ![]()
Сега сè е подготвено за примена на формулата ![]() . Отворете со ѕвездичка и „конструирајте го“ решението во согласност со десната страна:
. Отворете со ѕвездичка и „конструирајте го“ решението во согласност со десната страна:
Под интегралот повторно имаме полином за логаритам! Затоа, решението повторно се прекинува и по втор пат се применува правилото за интеграција по делови. Не заборавајте дека во слични ситуации логаритмот секогаш се означува.

Добро би било до сега да знаеш усно да ги најдеш наједноставните интеграли и изводи.

(1) Не се збунувајте за знаците! Многу често тука се губи минусот, исто така забележете дека минусот се однесува на на ситезаграда  , и овие загради треба правилно да се прошират.
, и овие загради треба правилно да се прошират.
(2) Отворете ги заградите. Го поедноставуваме последниот интеграл.
(3) Го земаме последниот интеграл.
(4) „Чешлање“ на одговорот.
Потребата да се примени правилото за интеграција по делови двапати (или дури три пати) не се јавува многу ретко.
И сега неколку примери за ваше решение:
Пример 3
Најдете го неопределен интеграл.
Овој пример се решава со промена на променливата (или замена под диференцијалниот знак)! Зошто да не - можете да се обидете да го земете во делови, ќе испадне смешна работа.
Пример 4
Најдете го неопределен интеграл.
Но, овој интеграл е интегриран со делови (ветената дропка).
Ова се примери што треба сами да ги решите, решенија и одговори на крајот од лекцијата.
Се чини дека во примерите 3 и 4 интеградите се слични, но методите за решавање се различни! Ова е главната тешкотија во совладувањето на интегралите - ако изберете погрешен метод за решавање на интеграл, тогаш можете да го чепкате со часови, како со вистинска загатка. Затоа, колку повеќе решавате разни интеграли, толку подобро, толку полесно ќе биде тестот и испитот. Дополнително, во втората година ќе има диференцијални равенки, а без искуство во решавање интеграли и изводи нема што да се прави таму.
Во однос на логаритмите, ова е веројатно повеќе од доволно. Како настрана, можам да се сетам и дека студентите по инженерство користат логаритми за да ги нарекуваат женските гради =). Патем, корисно е да се знаат напамет графиконите на главните елементарни функции: синус, косинус, арктангенс, експонент, полиноми од трет, четврти степен итн. Не, се разбира, кондом на земјината топка
Нема да го истегнам, но сега ќе запомните многу од делот Графикони и функции =).
Интеграли на експоненцијал помножен со полином
Општо правило:
Пример 5
Најдете го неопределен интеграл.
![]()
Користејќи познат алгоритам, интегрираме по делови:


Ако имате потешкотии со интегралот, тогаш треба да се вратите на статијата Метод на промена на променливата во неопределен интеграл.
Единственото друго нешто што можете да направите е да го измените одговорот:

Но, ако вашата техника за пресметка не е многу добра, тогаш најпрофитабилната опција е да ја оставите како одговор ![]() или дури
или дури ![]()
Односно, примерот се смета за решен кога ќе се земе последниот интеграл. Нема да биде грешка, тоа е друго прашање што наставникот може да побара од вас да го поедноставите одговорот.
Пример 6
Најдете го неопределен интеграл.
Ова е пример за да го решите сами. Овој интеграл е интегриран двапати со делови. Посебно внимание треба да се посвети на знаците - лесно е да се збуниме во нив, исто така се сеќаваме дека ова е сложена функција.
Нема што повеќе да се каже за изложувачот. Можам само да додадам дека експоненцијалниот и природниот логаритам се меѓусебно инверзни функции, ова сум јас на тема забавни графикони од вишата математика =) Стоп, застани, не се секирај, предавачот е трезен.
Интеграли на тригонометриски функции помножени со полином
Општо правило: for секогаш означува полином
Пример 7
Најдете го неопределен интеграл.
![]()
Ајде да се интегрираме по делови:


Хммм...и нема што да се коментира.
Пример 8
Најдете го неопределен интеграл ![]()
Ова е пример за да се решите сами
Пример 9
Најдете го неопределен интеграл
Друг пример со дропка. Како и во двата претходни примери, for означува полином.
Ајде да се интегрираме по делови: 

Доколку имате потешкотии или недоразбирања со наоѓање на интегралот, препорачувам да присуствувате на лекцијата Интеграли на тригонометриски функции.
Пример 10
Најдете го неопределен интеграл ![]()
Ова е пример за да го решите сами.
Совет: Пред да го користите методот интеграција по делови, треба да користите некоја тригонометриска формула која го претвора производот од две тригонометриски функции во една функција. Формулата може да се користи и при примена на методот на интеграција по делови, кој и да е попогоден за вас.
Тоа е веројатно сè во овој пасус. Поради некоја причина се сетив на еден ред од химната за физика и математика „И синусниот график оди бран по бран по оската на апсцисата“….
Интеграли на инверзни тригонометриски функции.
Интеграли на инверзни тригонометриски функции помножени со полином
Општо правило: секогаш ја означува инверзната тригонометриска функција.
Дозволете ми да ве потсетам дека инверзните тригонометриски функции вклучуваат лаксин, аркозин, арктангенс и лактангенс. Заради краткост на записот ќе ги наречам „арки“
Не можеме секогаш да пресметаме антидеривативни функции, но проблемот со диференцијација може да се реши за која било функција. Затоа не постои единствен метод на интеграција кој може да се користи за било кој тип на пресметка.
Во овој материјал ќе погледнеме примери за решавање проблеми поврзани со наоѓање на неопределен интеграл и ќе видиме за кои типови интегради е погоден секој метод.
Метод на директна интеграција
Главниот метод за пресметување на антидеривативната функција е директна интеграција. Ова дејство се заснова на својствата на неопределен интеграл, а за пресметките потребна ни е табела на антидеривати. Другите методи можат само да помогнат да се доведе оригиналниот интеграл во табеларна форма.
Пример 1
Пресметај го множеството антидеривати на функцијата f (x) = 2 x + 3 2 · 5 x + 4 3 .
Решение
Прво, да ја промениме формата на функцијата во f (x) = 2 x + 3 2 5 x + 4 3 = 2 x + 3 2 5 x + 4 1 3.
Знаеме дека интегралот од збирот на функции ќе биде еднаков на збирот на овие интеграли, што значи:
∫ f (x) d x = ∫ 3 2 5 x + 4 3 = 2 x + 3 2 5 x + 4 1 3 d x = ∫ 3 2 5 x + 4 1 3 d x
Го изведуваме нумеричкиот коефициент зад интегралниот знак:
∫ f (x) d x = ∫ 2 x d x + ∫ 3 2 (5 x + 4) 1 3 d x = = ∫ 2 x d x + 2 3 ∫ (5 x + 4) 1 3 d x
За да го најдеме првиот интеграл, ќе треба да се повикаме на табелата со антидеривати. Од него ја земаме вредноста ∫ 2 x d x = 2 x ln 2 + C 1
За да го пронајдете вториот интеграл, ќе ви треба табела со антидеривати за функцијата моќност ∫ x p · d x = x p + 1 p + 1 + C , како и правилото ∫ f k · x + b d x = 1 k · F (k · x + b) + C.
Затоа, ∫ f (x) d x = ∫ 2 x d x + 3 2 ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 3 20 (5 x + 4) 4 3 + C 2 = = 2 x ln 2 + 9 40 5 x + 4 4 3 + C
Го добивме следново:
∫ f (x) d x = ∫ 2 x d x + 3 2 ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 3 20 (5 x + 4) 4 3 + C 2 = = 2 x ln 2 + 9 40 5 x + 4 4 3 + C
со C = C 1 + 3 2 C 2
Одговор:∫ f (x) d x = 2 x ln 2 + 9 40 5 x + 4 4 3 + C
Посветивме посебна статија на директна интеграција користејќи табели на антидеривати. Ви препорачуваме да се запознаете со него.
Метод на замена
Овој метод на интеграција се состои во изразување на интеграндот преку нова променлива воведена специјално за оваа намена. Како резултат на тоа, треба да добиеме табеларна форма на интегралот или едноставно помалку сложен интеграл.
Овој метод е многу корисен кога треба да интегрирате функции со радикали или тригонометриски функции.
Пример 2
Оцени го неопределениот интеграл ∫ 1 x 2 x - 9 d x.
Решение
Да додадеме уште една променлива z = 2 x - 9 . Сега треба да го изразиме x во однос на z:
z 2 = 2 x - 9 ⇒ x = z 2 + 9 2 ⇒ d x = d z 2 + 9 2 = z 2 + 9 2 "d z = 1 2 z d z = z d z
∫ d x x 2 x - 9 = ∫ z d z z 2 + 9 2 z = 2 ∫ d z z 2 + 9
Ја земаме табелата со антидеривати и дознаваме дека 2 ∫ d z z 2 + 9 = 2 3 a r c t g z 3 + C .
Сега треба да се вратиме на променливата x и да го добиеме одговорот:
2 3 a r c t g z 3 + C = 2 3 a r c t g 2 x - 9 3 + C
Одговор:∫ 1 x 2 x - 9 d x = 2 3 a r c t g 2 x - 9 3 + C.
Ако треба да интегрираме функции со ирационалност од формата x m (a + b x n) p, каде што вредностите m, n, p се рационални броеви, тогаш важно е правилно да формулираме израз за воведување нова променлива. Прочитајте повеќе за ова во написот за интегрирање на ирационални функции.
Како што рековме погоре, методот на замена е лесен за употреба кога треба да интегрирате тригонометриска функција. На пример, користејќи универзална замена, можете да го намалите изразот на фракционо рационална форма.
Овој метод го објаснува правилото за интеграција ∫ f (k · x + b) d x = 1 k · F (k · x + b) + C .
Додаваме уште една променлива z = k x + b. Го добиваме следново:
x = z k - b k ⇒ d x = d z k - b k = z k - b k "d z = d z k
Сега ги земаме добиените изрази и ги додаваме во интегралот наведен во условот:
∫ f (k x + b) d x = ∫ f (z) d z k = 1 k ∫ f (z) d z = = 1 k F z + C 1 = F (z) k + C 1 k
Ако прифатиме C 1 k = C и се вратиме на оригиналната променлива x, тогаш добиваме:
F (z) k + C 1 k = 1 k F k x + b + C
Начин на запишување на диференцијалниот знак
Овој метод се заснова на трансформирање на интеграндот во функција од формата f (g (x)) d (g (x)). По ова, вршиме замена со воведување на нова променлива z = g (x), наоѓаме антидериват за неа и се враќаме на оригиналната променлива.
∫ f (g (x)) d (g (x)) = g (x) = z = ∫ f (z) d (z) = = F (z) + C = z = g (x) = F ( g(x)) + C
За побрзо решавање на проблемите со користење на овој метод, имајте при рака табела со деривати во форма на диференцијали и табела со антидеривати за да го најдете изразот на кој интеградот ќе треба да се намали.
Дозволете ни да анализираме проблем во кој треба да го пресметаме множеството антидеривати на функцијата котангента.
Пример 3
Пресметај го неопределениот интеграл ∫ c t g x d x.
Решение
Ајде да го трансформираме оригиналниот израз под интеграл користејќи основни тригонометриски формули.
c t g x d x = cos s d x sin x
Ја гледаме табелата со деривати и гледаме дека броителот може да се подведе под диференцијалниот знак cos x d x = d (sin x), што значи:
c t g x d x = cos x d x sin x = d sin x sin x, т.е. ∫ c t g x d x = ∫ d sin x sin x.
Да претпоставиме дека sin x = z, во овој случај ∫ d sin x sin x = ∫ d z z. Според табелата со антидеривати, ∫ d z z = ln z + C . Сега да се вратиме на првобитната променлива ∫ d z z = ln z + C = ln sin x + C .
Целото решение може накратко да се напише на следниов начин:
∫ с t g x d x = ∫ cos x d x sin x = ∫ d sin x sin x = s i n x = t = = ∫ d t t = ln t + C = t = грев x = ln грев x + C
Одговор: ∫ c t g x d x = ln sin x + C
Методот на претплата на диференцијалниот знак многу често се користи во пракса, па затоа ве советуваме да прочитате посебна статија посветена на него.
Начин на интеграција по делови
Овој метод се заснова на трансформирање на интеграндот во производ од формата f (x) d x = u (x) v " x d x = u (x) d (v (x)), по што формулата ∫ u (x) d ( v (x)) = u (x) v (x) - ∫ v (x) d u (x) Ова е многу удобен и вообичаен метод за решавање Понекогаш делумната интеграција во еден проблем треба да се примени неколку пати пред да се добие посакуваниот резултат.
Дозволете ни да анализираме проблем во кој треба да го пресметаме множеството антидеривати на арктангенсот.
Пример 4
Пресметај го неопределениот интеграл ∫ a r c t g (2 x) d x .
Решение
Да претпоставиме дека u (x) = a r c t g (2 x), d (v (x)) = d x, во овој случај:
d (u (x)) = u " (x) d x = a r c t g (2 x) "d x = 2 d x 1 + 4 x 2 v (x) = ∫ d (v (x)) = ∫ d x = x
Кога ја пресметуваме вредноста на функцијата v (x), не треба да додаваме произволна константа C.
∫ a r c t g (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = x a r c t g (2 x) - ∫ 2 x d x 1 + 4 x 2
Добиениот интеграл го пресметуваме користејќи го методот на подведување на диференцијалниот знак.
Бидејќи ∫ a r c t g (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = x a r c t g (2 x) - ∫ 2 x d x 1 + 4 x 2, тогаш 2 x d x = 1 4 d (1 + 4 x 2) .
∫ a r c t g (2 x) d x = x · a r c t g (2 x) - ∫ 2 x d x 1 + 4 x 2 = = x · a r c t g (2 x) - 1 4 ln 1 + 4 x 2 + C 1 = = x · a r c t g (2 x) - 1 4 ln 1 + 4 x 2 + C
Одговор:∫ a r c t g (2 x) d x = x · a r c t g (2 x) - 1 4 ln 1 + 4 x 2 + C .
Главната тешкотија при користењето на овој метод е потребата да се избере кој дел да се земе како диференцијал, а кој дел како функција u (x). Написот за начинот на интеграција по делови дава неколку совети за ова прашање со кои треба да се запознаете.
Ако треба да го најдеме множеството антидеривати на фракционо рационална функција, тогаш прво мора да го претставиме интеграндот како збир од едноставни дропки, а потоа да ги интегрираме добиените дропки. За повеќе информации, видете ја статијата за интегрирање едноставни дропки.
Ако интегрираме израз на моќ од формата sin 7 x · d x или d x (x 2 + a 2) 8, тогаш ќе имаме корист од формулите за повторување кои постепено можат да ја намалат моќноста. Тие се изведени со користење на секвенцијална повторена интеграција по делови. Препорачуваме да ја прочитате статијата „Интеграција со помош на формули за повторување.
Да резимираме. За да се решат проблемите, многу е важно да се знае методот на директна интеграција. Други методи (замена, замена, интеграција по делови) исто така ви овозможуваат да го поедноставите интегралот и да го доведете во табеларна форма.
Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter
Методот на интеграција по делови се користи кога е потребно да се поедностави постоечкиот неопределен интеграл или да се намали на табеларна вредност. Најчесто се користи во присуство на експоненцијални, логаритамски, директни и инверзни тригонометриски формули и нивни комбинации во интеграндот.
Основната формула потребна за користење на овој метод е:
∫ f (x) d x = ∫ u (x) d (v (x)) = u (x) v (x) - ∫ v (x) d (u (x))
Тоа значи дека прво треба да го претставиме изразот под интегралот како производ на функцијата u (x) и диференцијалот на функцијата v (x). По ова, ја пресметуваме вредноста на функцијата v (x) со некој метод (најчесто се користи методот на директна интеграција), а добиените изрази ги заменуваме во наведената формула, намалувајќи го оригиналниот интеграл на разликата u (x) v (x) - ∫ v (x) d(u(x)) . Добиениот интеграл може да се земе и со кој било метод на интеграција.
Да разгледаме проблем во кој треба да го најдеме множеството антидеривати на логаритамската функција.
Пример 1
Оцени го неопределениот интеграл ∫ ln (x) d x .
Решение
Го користиме методот на интеграција по делови. За да го направите ова, го земаме ln (x) како функција од u (x), а остатокот од интеграндот како d (v (x)). Како резултат на тоа, добиваме дека ln (x) d x = u (x) d (v (x)), каде што u (x) = ln (x), d (v (x)) = d x.
Диференцијалот на функцијата u(x) е d(u(x)) - u"(x)d x = d x x, а функцијата v(x) може да се запише како v(x) = ∫ d(v(x) ) = ∫ d x = x
Важно:константата C ќе се смета за еднаква на 0 при пресметување на функцијата v (x).
Ајде да го замениме она што го добивме во интеграцијата со формулата за делови:
∫ ln (x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = ln (x) x - ∫ x d x x = ln (x) x - ∫ d x = ln ( x) x - x + C 1 = = x (ln (x) - 1) + C
каде што C = - C 1
Одговор:∫ ln (x) d x = x (ln (x) - 1) + C .
Најтешкото нешто во примената на овој метод е да се избере кој дел од оригиналниот израз под интегралот да се земе како u (x) и кој како d (v (x)).
Ајде да погледнеме неколку стандардни случаи.
Ако нашата состојба содржи интеграли од формата ∫ P n (x) · e a x d x, ∫ P n (x) · sin (a x) d x или ∫ P n (x) · cos (a x) d x, каде што a е коефициент и P n (x) е полином со степен n, тогаш P n (x) мора да се земе како функција u (x).
Пример 2
Најдете го множеството антидеривати на функцијата f (x) = (x + 1) · sin (2 x) .
Решение
Можеме да го земеме неопределениот интеграл ∫ (x + 1) · sin (2 x) d x по делови. Го земаме x + 1 како u (x) и sin (2 x) d x како d (v (x)), односно d (u (x)) = d (x + 1) = d x.
Користејќи директна интеграција, добиваме:
v (x) = ∫ грев (2 x) d x = - 1 2 cos (2 x)
Заменете во интеграцијата со формулата за делови:
∫ (x + 1) sin (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = (x + 1) - 1 2 cos (2 x) - ∫ - 1 2 cos (2 x) d x = = - 1 2 (x + 1) cos (2 x) + 1 2 ∫ cos (2 x) d (x) = = - 1 2 (x + 1) cos ( 2 x) + 1 4 грев (2 x) + C
Одговор:∫ (x + 1) · sin (2 x) d x = - 1 2 (x + 1) · cos (2 x) + 1 4 sin (2 x) + C .
Пример 3
Оцени го неопределениот интеграл ∫ (x 2 + 2 x) e x d x .
Решение
Го земаме полиномот од втор ред x 2 + 2 x како u (x) и d (v (x)) - e x d x .
∫ x 2 + 2 x e x d x = u (x) = x 2 + 2 x, d (v (x)) = e x d x d (u (x)) = (2 x + 2) d x, v (x) = ∫ e x d x = e x = = u (x) v (x) - ∫ v (x) d (u (x)) = (x 2 + 2 x) e x - ∫ (2 x + 2) e x d x
На она што го добивме, повторно мора да го примениме методот на интеграција по делови:
∫ (2 x + 2) e x d x = (x 2 + 2 x) e x - ∫ 2 x + 2 e x d x = = u (x) = (2 x + 2) , d (v (x)) = e x d x d (u ( x)) = 2 d x, v (x) = ∫ e x d x = e x = = (x 2 + 2 x) e x - (2 x + 2) e x - ∫ v (x) d (u (x)) = = ( x 2 + 2 x) e x - (2 x + 2) e x - ∫ 2 e x d x = = (x 2 + 2 x - 2 x - 2) e x + 2 ∫ e x d x = (x 2 - 2) e x + 2 e x + C = x 2 e x + C
Одговор:∫ (x 2 + 2 x) e x d x = x 2 e x + C .
Пример 4
Оцени го интегралот ∫ x 3 cos 1 3 x d x.
Решение
Според методот на интеграција по делови, земаме u (x) = x 3 и d (v (x)) = cos 1 3 x d x.
Во овој случај, d (u (x)) = 3 x 2 d x и v (x) = ∫ cos 1 3 x d x = 3 sin 1 3 x .
Сега да ги замениме добиените изрази во формулата:
∫ x 3 cos 1 3 x d x = u (x) v (x) - ∫ v (x) d (u)) = = x 3 3 sin 1 3 x - ∫ 3 x 2 3 sin 1 3 x d x = = 3 x 3 грев 1 3 x - 9 ∫ x 2 грев 1 3 x d x
Имаме неопределен интеграл, кој повторно треба да се земе во делови:
∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x - 9 ∫ x 2 sin 1 3 x d x = = u (x) = x 2 , d (v (x)) = грев 1 3 x d x d (u (x )) = 2 x d x, v (x) = ∫ sin 1 3 x d x = - 3 cos 1 3 x = = 3 x 3 грев 1 3 x - 9 - 3 x 2 cos 1 3 x - ∫ - 3 cos 1 3 x · 2 x d x = = 3 x 3 грев 1 3 x + 27 x 2 · cos 1 3 x - 54 ∫ x cos 1 3 x d x
Повторно вршиме делумна интеграција:
∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x + 27 x 2 · cos 1 3 x - 54 ∫ x cos 1 3 x d x = = u (x) = x , d (v (x)) = cos 1 3 x d x d (u (x)) = d x, v (x) = ∫ cos 1 3 x d x = 3 грев 1 3 x = = 3 x 3 грев 1 3 x + 27 x 2 cos 1 3 x - 54 3 x грев 1 3 x - ∫ 3 грев 1 3 x d x = = 3 x 3 - 162 x грев 1 3 x + 27 x 2 cos 1 3 x + 162 ∫ грев 1 3 x d x = = (3 x 3 - 162 x) грев 1 3 x + 27 x 2 cos 1 3 x - 486 cos 1 3 x + C = = (3 x 3 - 162 x) грев 1 3 x + (27 x 2 - 486) cos 1 3 x + C
Одговор:∫ x 3 cos 1 3 x d x = (3 x 3 - 162 x) sin 1 3 x + (27 x 2 - 486) cos 1 3 x + C .
Ако нашата состојба содржи интеграли од формата ∫ P n (x) · ln (a x) d x , ∫ P n (x) · a r c sin (a x) d x, ∫ P n (x) · a r c cos (a x) d x, ∫ P n (x) · a r c t g (a x) d x, ∫ P n (x) · a r c c t g (a x) d x
тогаш треба да ги земеме како u (x) функциите a r c t g (a x) , a r c c t g (x) , ln (a x) , a r c sin (a x) , a r cos (a x) .
Пример 5
Пресметај го множеството антидеривати на функцијата (x + 1) ln (2 x) .
Решение
Го земаме ln (2 x) како u (x) и (x + 1) d x како d (v (x)). Добиваме:
d (u (x)) = (ln (2 x)) " d x = 1 2 x (2 x) " d x = d x x v (x) = ∫ (x + 1) d x = x 2 2 + x
Ајде да ги замениме овие изрази во формулата:
∫ (x + 1) ln (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = x 2 2 + x ln 2 x - ∫ x 2 2 + x d x x = = x 2 2 + x ln (2 x) - ∫ x 2 + 1 d x = x 2 2 + x ln 2 x - 1 2 ∫ x d x - ∫ d x = = x 2 2 + x ln (2 x) - x 2 4 - x + C
Одговор:∫ (x + 1) ln (2 x) d x = x 2 2 + x ln (2 x) - x 2 4 - x + C .
Пример 6
Оцени го неопределениот интеграл ∫ x · a r c sin (2 x) d x .
Решение
Одлучуваме кој дел да го земеме како u (x) и кој дел да го земеме како d (v (x)). Според правилото дадено погоре, треба да земете r c sin (2 x) како прва функција, и d (v (x)) = x d x. Добиваме:
d (u (x)) = (a r c sin (2 x) "d x = 2 x" d x 1 - (2 x) 2 = 2 d x 1 - (2 x) 2 , v (x) = ∫ x d x = x 2 2
Заменете ги вредностите во формулата:
∫ x · a r c sin (2 x) d x = u (x) v (x) - ∫ v (x) d (u (x)) = = x 2 2 a r c sin (2 x) - ∫ x 2 2 - 2 d x 1 - (2 x) 2 = x 2 2 a r c sin (2 x) - ∫ x 2 d x 1 - 4 x 2
Како резултат, дојдовме до следната еднаквост:
∫ x · a r c sin (2 x) d x = x 2 2 a r c sin (2 x) - ∫ x 2 d x 1 - 4 x 2
Сега да го пресметаме добиениот интеграл ∫ x 2 d x 1 - 4 x 2:
∫ x 2 d x 1 - 4 x 2 = ∫ x 2 d x 4 1 4 - x 2 = 1 2 ∫ x 2 d x 1 4 - x 2 = - 1 2 ∫ - x 2 d x 1 4 - x 2 = = - 1 2 ∫ 1 4 - x 2 - 1 4 1 4 - x 2 d x = - 1 2 1 4 - x 2 d x + 1 8 ∫ d x 1 4 - x 2 = = - 1 2 ∫ 1 4 - x 2 d x + 1 8 a r c грев (2 x)
Овде можете да го примените методот на интеграција по делови и да добиете:
∫ x 2 d x 1 - 4 x 2 = - 1 2 ∫ 1 4 - x 2 d x + 1 8 a r c sin (2 x) = = u (x) = 1 4 - x 2 , d (v (x)) = d x d (u (x)) = 1 4 - x 2 "d x 2 1 4 - x 2 = - x d x 1 4 - x 2, v (x) = ∫ d x = x = = - 1 2 u (x) v ( x) - ∫ v (x) d (u (x)) + 1 8 a r c sin (2 x) = = - 1 2 x 1 4 - x 2 - ∫ - x 2 d x 1 4 - x 2 + 1 8 a r c грев (2 x) = = - 1 2 x 1 4 - x 2 - 1 2 ∫ x 2 d x 1 4 - x 2 + 1 8 a r c грев (2 x) = = - 1 2 x 1 4 - x 2 - ∫ x 2 d x 1 - 4 x 2 + 1 8 a r c sin (2 x)
Сега нашата еднаквост изгледа вака:
∫ x 2 d x 1 - 4 x 2 = - 1 2 x 1 4 - x 2 - ∫ x 2 d x 1 - 4 x 2 + 1 8 a r c sin (2 x)
Гледаме дека интегралот од десната страна е сличен на оној од левата страна. Го преместуваме на друг дел и добиваме:
2 ∫ x 2 d x 1 - 4 x 2 = - 1 2 x 1 4 - x 2 + 1 8 a r c sin (2 x) + C 1 ⇒ x 2 d x 1 - 4 x 2 = - 1 4 x 1 4 - x 2 + 1 16 a r c sin (2 x) + C 2 x 2 d x 1 - 4 x 2 = - 1 8 x 1 4 - x 2 + 1 16 a r c sin (2 x) + C 2
каде што C 2 = C 1 2
Да се вратиме на оригиналните променливи:
∫ x · a r c sin (2 x) d x = x 2 2 a r c sin (2 x) - ∫ x 2 d x 1 - 4 x 2 = = x 2 2 a r c sin (2 x) - - 1 8 x 1 - 4 x 2 + 1 16 a r c sin (2 x) + C 2 = = 1 2 x 2 - 1 8 a r c sin (2 x) + 1 8 x 1 - 4 x 2 + C
каде што C = - C 2
Одговор:∫ x · a r c sin (2 x) d x = 1 2 x 2 - 1 8 a r c sin (2 x) + 1 8 x 1 - 4 x 2 + C .
Ако нашиот проблем содржи интеграл од формата ∫ e a · x · sin (b x) d x или ∫ e a · x · cos (b x) d x, тогаш која било функција може да се избере како u (x).
Пример 7
Оцени го неопределениот интеграл ∫ e x · sin (2 x) d x .
Решение
∫ e x sin (2 x) d x = u (x) = sin (2 x) , d (v (x)) = e x d x d (u (x)) = 2 cos (2 x) d x, v (x) = ∫ e x d x = e x = = u (x) v (x) - ∫ v (x) d (u (x)) = грев (2 x) e x - ∫ e x 2 cos 2 x d x = = грев (2 x) e x - 2 ∫ e x cos (2 x) d x = u (x) = cos (2 x) , d (v (x)) = e x d x d (u (x)) = - 2 sin (2 x) d x, v (x) = ∫ e x d x = e x = = грев (2 x) e x - 2 cos (2 x) e x - ∫ (e x (- 2 sin (2 x) d x)) = = грев (2 x) e x = 2 cos (2 x) e x - 4 ∫ e x sin (2 x) d x
Како резултат, ќе добиеме:
∫ e x sin (2 x) d x = sin (2 x) e x - 2 cos (2 x) e x - 4 ∫ e x sin (2 x) d x
Ги гледаме истите интеграли лево и десно, што значи дека можеме да претставиме слични термини:
5 ∫ e x sin (2 x) d x = sin (2 x) e x - 2 cos (2 x) e x ⇒ ∫ e x sin (2 x) d x = 1 5 sin (2 x) e x - 2 5 cos (2 x) e x + C
Одговор: ∫ e x sin (2 x) d x = 1 5 sin (2 x) e x - 2 5 cos (2 x) e x + C
Овој метод на решение е стандарден, а десно често добивате интеграл кој е идентичен со оригиналниот.
Ги разгледавме најтипичните проблеми во кои можете точно да одредите кој дел од изразот да го земете како d (v (x)), а кој дел како u (x). Во други случаи, ова треба сами да го одредите.
Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter