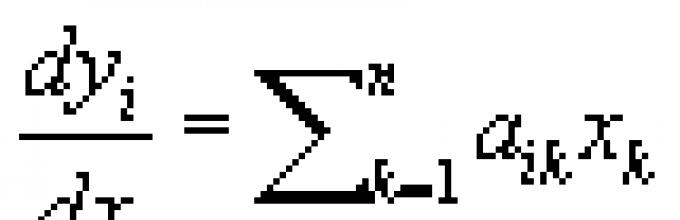) А = ||а ик||n 1 со одземање на вредноста λ од дијагоналните елементи. Оваа детерминанта е полином во однос на X - карактеристичен полином. Кога ќе се отвори, X. u. е напишано вака:

Каде С 1 = а 11 + а 22 +... ан- т.н матрична трага, С 2е збир на сите главни минори од втор ред, т.е. минори од формата i k), итн., и С n- матрична детерминанта А. Корените на H. u. λ 1 , λ 2 ,..., λ nсе нарекуваат сопствени вредности на матрицата А. За вистинска симетрична матрица, како и за хермитска матрица, сите λ ксе реални, вистинска косо-симетрична матрица ги има сите λ кчисто имагинарни броеви; во случај на реална ортогонална матрица, како и унитарна матрица, сите |λ к| = 1.

Х.у. пронајдени во широк спектар на области на математика, механика, физика и технологија. Во астрономијата, при определувањето на секуларните пертурбации на планетите, тие доаѓаат и до хемиски равенки; оттука и второто име за X. u. - вековна равенка.

2) H. u. линеарна диференцијална равенка со константни коефициенти

а 0λ y (n) + на 1 год (n-1) +... + n-1 год" + а н г = 0

Алгебарска равенка која се добива од дадена диференцијална равенка по промена на функцијата наи неговите деривати со соодветните сили на λ, т.е. равенката

а 0λ n + а 1λ n-1 + ... + а n-1 y" + а н г = 0.

До оваа равенка се доаѓа со изнаоѓање на одредено решение на формата на = види λ Xза дадена диференцијална равенка. За систем на линеарни диференцијални равенки

Х.у. напишано со помош на детерминанта

Х.у. матрици А =

Голема советска енциклопедија. - М.: Советска енциклопедија. 1969-1978 .

Погледнете што е „Карактеристична равенка“ во другите речници:

    Во многу случаи, физичките процеси што се случуваат во системите се опишани со систем на обични линеарни диференцијални равенки со константни коефициенти, што во прилично општ случај може да се сведе на диференцијалната равенка ... Енциклопедија на технологијата

    Алгебарска равенка на формата: Детерминантата во оваа формула се добива од детерминантата на матрицата со одземање на вредноста x од дијагоналните елементи; тој претставува полином во x и се нарекува карактеристичен полином... Голем енциклопедиски речник

    карактеристична равенка- - [В.А. Семенов. Англиско-руски речник за релејна заштита] Теми релејна заштита EN карактеристична равенка ... Водич за технички преведувач

    Алгебарска равенка на формата. Детерминантата во оваа формула се добива од детерминантата на матрицата x на дијагоналните елементи; тој е полином во x и се нарекува карактеристичен полином. * * * КАРАКТЕРИСТИЧНО…… Енциклопедиски речник

    карактеристична равенка- būdingoji lygtis statusas T sritis automatika atitikmenys: engl. карактеристична равенка; изведба равенка vok. Charakteristische Gleichung, f; Stammgleichung, f rus. карактеристична равенка, n pranc. Карактеристична равенка, f …

    карактеристична равенка- būdingoji lygtis statusas T sritis fizika atitikmenys: ингли. карактеристична равенка; изведба равенка vok. Charakteristische Gleichung, f rus. карактеристична равенка, n pranc. Карактеристичка равенка, ѓ … Физички термини

    карактеристична равенка Енциклопедија „Авијација“

    карактеристична равенка- карактеристична равенка. Во многу случаи, физичките процеси што се случуваат во системите се опишани со систем на обични линеарни диференцијални равенки со константни коефициенти, кои во прилично општ случај може да се намалат... Енциклопедија „Авијација“

    Секуларна равенка, види чл. Карактеристичен полином... Математичка енциклопедија

    Карактеристичен полином е полином кој ги одредува сопствените вредности на матрицата. Друго значење: Карактеристичниот полином на линеарен рекурент е полином. Содржина 1 Дефиниција ... Википедија

Книги

  • Карактеристични Lie rings и нелинеарни интеграбилни равенки, Zhiber A.V.. Книгата е посветена на систематско прикажување на алгебарскиот пристап кон проучувањето на нелинеарни интеграбилни парцијални диференцијални равенки и нивните дискретни аналози, врз основа на концептот...

Слободниот режим на колото не зависи од изворите на енергија, тој се одредува само од структурата на колото и параметрите на неговите елементи. Од ова произлегува дека корените на карактеристичната равенка p1, p2,..., pn ќе бидат исти за сите променливи функции (струи и напони).

Карактеристичната равенка може да се конструира со користење на различни методи. Првиот метод е класичен, кога карактеристичната равенка е составена строго во согласност со диференцијалната равенка според класичната шема. При пресметување на минливи процеси во сложено коло, се составува систем од „m“ диференцијални равенки според законите на Кирхоф за дијаграмот на колото по префрлувањето. Бидејќи корените на карактеристичната равенка се заеднички за сите променливи, решението на системот на диференцијални равенки се врши во однос на која било променлива (опционално). Како резултат на решението се добива нехомогена диференцијална равенка со една променлива. Составете карактеристична равенка во согласност со добиената диференцијална равенка и определете ги нејзините корени.

Пример. Нацртај карактеристична равенка и определи ги нејзините корени за променливите од дијаграмот на сл. 59.1. Параметрите на елементите се наведени во општа форма.

Систем на диференцијални равенки според законите на Кирхоф:

Да го решиме системот на равенки за променливата i3, како резултат на тоа добиваме нехомогена диференцијална равенка:

Вториот начин да се состави карактеристична равенка е да се изедначи на нула главната детерминанта на Кирхофовиот систем на равенки за променливите со слободни компоненти.

Нека слободната компонента на произволна струја има форма iksv = Аkept, тогаш:

Системот на равенки за слободните компоненти се добива од Кирхофовиот систем на диференцијални равенки со замена на изводите на променливите со факторот p, а интегралите со 1/p. За примерот што се разгледува, системот на равенки за слободни компоненти има форма:

Карактеристична равенка и нејзиниот корен:


Третиот начин да се состави карактеристична равенка (инженерство) е да се изедначи отпорноста на влезниот оператор на колото на нула во однос на која било од неговите гранки.

Отпорот на операторот на елементот се добива од неговиот комплексен отпор со едноставно замена на факторот jω со p, затоа

За примерот за кој станува збор:


Третиот метод е наједноставен и најекономичен, затоа најчесто се користи при пресметување на минливи процеси во електрични кола.

Корените на карактеристичната равенка го карактеризираат слободниот преоден процес во коло без извори на енергија. Овој процес се случува со загуби на енергија и затоа се распаѓа со текот на времето.

Во општиот случај, редоследот на диференцијалната равенка што го опишува минливиот процес во колото и, следствено, степенот на карактеристичната равенка и бројот на нејзините корени се еднакви на бројот на независни почетни услови, или бројот на независни уреди за складирање на енергија (намотки L и кондензатори C).

Ако дијаграмот на колото содржи паралелно поврзани кондензатори C1, C2,... или сериски поврзани намотки L1, L2,..., тогаш кога се пресметуваат преодните процеси тие мора да се заменат со еден еквивалентен елемент SE = C1 + C2+... или LE = L1 + L2+...

Така, општата форма на решението за која било променлива при пресметување на минливиот процес може да се состави само од анализа на дијаграмот на колото, без да се состави и реши систем на диференцијални равенки.

За примерот дискутиран погоре.

  • Карактеристичната равенка се составува за колото по префрлувањето. Може да се добие на следниве начини:
  • директно врз основа на диференцијална равенка од формата (2) (види предавање бр. 24), т.е. со исклучување од системот на равенки што ја опишуваат електромагнетната состојба на колото врз основа на првиот и вториот закон на Кирхоф, сите непознати величини освен една, во однос на која е напишана равенката (2);
  • со користење на израз за влезната импеданса на синусоидално струјно коло;

врз основа на изразот на главната детерминанта.

Според првиот метод, на претходното предавање е добиена диференцијална равенка во однос на напонот на кондензаторот за сериско коло R-L-C, врз основа на кое се запишува карактеристичната равенка.

Треба да се забележи дека, бидејќи линеарното коло е покриено со еден преоден процес, корените на карактеристичната равенка се заеднички за сите слободни компоненти на напоните и струите на гранките на колото, чии параметри се вклучени во карактеристичната равенка. Според тоа, според првиот метод на составување на карактеристична равенка, секоја променлива може да се избере како променлива во однос на која е напишана.

Да ја разгледаме примената на вториот и третиот метод за составување на карактеристичната равенка користејќи го примерот на колото на сл. 1.

Составот на карактеристичната равенка со користење на методот на влезна отпорност е како што следува:

се евидентира влезниот отпор на колото за наизменична струја;

jw се заменува со оператор p;

добиениот израз е еднаков на нула.

Равенка

Треба да се нагласи дека влезниот отпор може да се запише во однос на точката на прекин на која било гранка на колото. Во овој случај, активната дво-терминална мрежа се заменува со пасивна по аналогија со методот на еквивалентен генератор. Овој метод на составување на карактеристичната равенка претпоставува отсуство на магнетно споени гранки во колото; доколку ги има, потребно е да се изврши нивно прелиминарно одврзување.

За колото на сл. 1 во однос на изворните терминали

.

Заменувајќи го jw со p и изедначувајќи го добиениот израз на нула, пишуваме

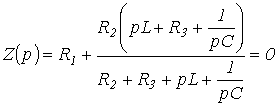
. (1)

При составување на карактеристична равенка врз основа на изразот на главната детерминанта, бројот на алгебарски равенки врз основа на кои се пишува е еднаков на бројот на непознати компоненти на слободна струја. Алгебризацијата на оригиналниот систем на интегро-диференцијални равенки, составена, на пример, врз основа на законите на Кирхоф или методот на контурни струи, се врши со замена на симболите на диференцијација и интеграција, соодветно, со множење и делење од страна на операторот стр. Карактеристичната равенка се добива со изедначување на напишаната детерминанта на нула. Бидејќи изразот за главната детерминанта не зависи од десните страни на системот на нехомогени равенки, тој може да се состави врз основа на систем на равенки напишан за вкупните струи.

За колото на сл. 1 алгебризиран систем на равенки врз основа на методот на струја на јамка има форма

Оттука и изразот за главната детерминанта на овој систем

Изедначувајќи го D на нула, добиваме резултат сличен на (1).

Општа методологија за пресметување на минливи процеси со користење на класичен метод

Општо земено, методологијата за пресметување на минливи процеси со користење на класичниот метод ги вклучува следните чекори:

Примери за пресметување на минливи процеси со користење на класичен метод

1. Преодни процеси во колото R-L кога е поврзано со извор на напон

Таквите процеси се случуваат, на пример, при поврзување на електромагнети, трансформатори, електрични мотори итн. со извор на енергија.

Да разгледаме два случаи:

Според разгледуваниот метод за струјата во колото на сл. 2 може да се напише

Карактеристична равенка

па оттука и временската константа .

Така,

. (5)

Заменувајќи ги (4) и (5) во релацијата (3), пишуваме

.

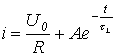Според првиот закон за комутација. Потоа

,

Така, струјата во колото за време на минливиот процес е опишана со равенката

,

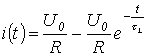а напонот на индукторот е даден со

.

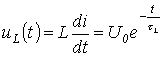Квалитативниот изглед на кривите и соодветните на добиените решенија е претставен на сл. 3.

За вториот тип на извор, принудната компонента се пресметува со помош на симболичкиот метод:

,

Изразот на слободната компонента не зависи од типот на изворот на напон. Оттука,

.

Оттогаш

Така, конечно добиваме

. (6)

Анализата на добиениот израз (6) покажува:

Ако е значајна по големина, тогаш во текот на половина период слободната компонента не се намалува значително. Во овој случај, максималната вредност на преодната струја може значително да ја надмине амплитудата на струјата во стабилна состојба. Како што може да се види од сл. 4, каде

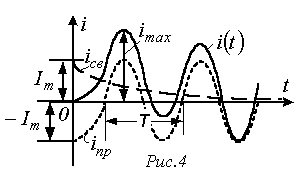
, максималната струја се јавува по приближно . Во границата во.

Така, за линеарно коло, максималната вредност на преодната струја не може да надмине двапати од амплитудата на присилната струја: .

Слично за линеарно коло со кондензатор: ако во моментот на префрлување принудниот напон е еднаков на неговата амплитудна вредност и временската константа на колото е доволно голема, тогаш по околу половина период напонот на кондензаторот ја достигнува својата максимална вредност , што не може да надмине двапати од амплитудата на принудниот напон: .

2. Преодни процеси при исклучување на индукторот од изворот на енергија

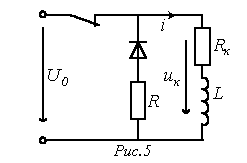
Кога клучот е отворен во колото на сл. 5 принудна компонента на струјата низ индукторот.

Карактеристична равенка

,

каде И .

Според првиот закон за комутација

.

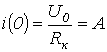Така, изразот за минлива струја е

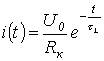
и напонот преку индукторот

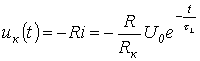. (7)

Анализата (7) покажува дека кога се отвораат кола кои содржат индуктивни елементи, може да настанат големи пренапони, кои без преземање посебни мерки може да ја оштетат опремата. Навистина, кога Напонскиот модул на индукторот во моментот на префрлување ќе биде многукратно поголем од изворниот напон: . Во отсуство на отпорник за гаснење R, наведениот напон се применува на контактите за отворање на клучот, како резултат на што се јавува лак меѓу нив.

3. Полнење и празнење на кондензатор

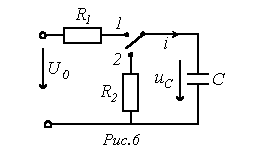
Кога клучот ќе се премести во позиција 1 (види слика 6), започнува процесот на полнење на кондензаторот:

.

Компонента со принуден напон на кондензатор.

Од карактеристичната равенка

се одредува коренот . Оттука и временската константа.

Карактеристичната равенка има форма:

За да се одреди типот на слободната компонента потребно е да се изготви и реши карактеристичната равенка: z(p) = 0. За да се напише карактеристичната равенка потребно е да се нацрта дијаграм во кој сите извори на emf и струја треба да бидат се заменуваат со сопствен внатрешен отпор, а отпорот на индуктивноста и капацитетот треба да се земат соодветно еднакви Pl и , тогаш е неопходно да се прекине која било гранка од ова коло, да се запише неговиот почетен отпор во однос на точките на прекин, да се изедначи на нула, реши и определи ги корените на p, ако корените се покажат како вистински негативни, тогаш слободната компонента на саканата функција:

,каде m е бројот на корените на равенката;

Корени; - трајно интегриран.

Ако корените на равенката на знаците се покажат како сложени конјугирани, тогаш слободната состојба ќе ја има формата:

каде е фреквенцијата на слободни вибрации;

Почетна фаза на слободни осцилации.

8. Време на транзиција. Определување на практично t pp. Пресметка на времето на процесот на транзиција.

Времето на минливиот процес зависи од коефициентот на слабеење. Вредноста зависи од колото и параметрите Значи за коло со сериско поврзување r и L = и за сериско поврзување

95% завршување на процесот на транзиција 3.

Најлесен начин да се конструираат кривите на слободните компоненти на минливиот процес е да се постават вредностите на времето t на 0, ,2.....Ако има неколку реални корени, тогаш добиената крива се добива со собирање на ординати на поединечните термини (сл. 1.)

Слика 1:

9.10, Преоден процес во r, C – кола кога е поврзан со извор на постојан напон. Изведете ја анализата со класичен метод; даде аналитички изрази за U C (t); iC(t); графика. (Класичен метод).

Равенката на состојбата на rC колото по префрлувањето е како што следува:

(1) или rC (2)

Неговото решение:

Капацитетот C по затворањето на клучот на t ќе се наплаќа до стабилна вредност

Бидејќи првичните услови се нула, според законот за комутација на t=0, или 0=A, од каде A=-E.

Решението на равенката (2) ќе има форма:

Струја на колото i(t)=C

Слика 1.

Слика 2.

Графиконите на промените на напонот и струјата i(t) се прикажани на сликите 1 и 2. Од сликите може да се види дека напонот на кондензаторот експоненцијално се зголемува од 0 до E, додека моменталната јачина во моментот на префрлување нагло достигнува вредноста E/r, а потоа се намалува на нула.

11.12. Преоден процес во r, C – кола кога е поврзан со синусоидален извор на напон. Изведете ја анализата со класичен метод; даде аналитички изрази за U C (t); iC(t); графика. (Класичен метод).

Равенката на состојбата на rC колото во преодниот режим е следна

rC .

Решение на оваа равенка:

Бесплатна компонента

каде =rC

Бидејќи колото е линеарно, тогаш со синусоидален ефект и во стабилна состојба, напонот на кондензаторот исто така ќе се промени според синусоидален закон со фреквенцијата на влезниот ефект :

;

Имајќи предвид дека j= , добиваме:

Интеграциона константа А на слободната компонента

Да најдеме од почетните услови во колото земајќи го предвид законот за комутација:

.На t=0 последниот израз ја има формата

Каде A=-

Додавајќи ги компонентите и , го добиваме конечниот израз за напонот преку кондензаторот во преоден режим:

= + = - (1)

Анализата на изразот (1) покажува дека минливиот процес во rC колото под синусоидално влијание зависи од почетната фаза на изворот emf во моментот на префрлување и од временската константа на rC колото.

Ако , тогаш =0 и стабилна состојба ќе се појави во колото веднаш по префрлувањето, т.е.

Кога напон = - , т.е. Напонот преку кондензаторот веднаш по префрлувањето може да достигне речиси двојно поголема вредност од позитивниот знак, а потоа постепено да се приближува до =.

Фазната разлика ќе ја доведе равенката (1) до формата:

Разликата помеѓу овој режим и претходниот е во тоа што напонот преку кондензаторот веднаш по префрлувањето може да достигне речиси двојно поголема негативна вредност.

За разгледуваното Rc коло со синусоидален извор на струја во стабилна состојба, почетната фаза на влезниот напон не игра никаква улога, но во минливиот процес неговото влијание е значајно.

13. Преоден процес во r, L, C – кола кога е поврзан со извор на постојан напон. Сериски процес. Аналитички изрази за i(t), графика. (Класичен метод).

Корените се реални, негативни, различни.

I(t)=I уста +A1e p 1 t +A2e p 2 t

Процесот е периодичен:

t=0 (i(0)=A1+A2; A1=-A2

{

t=0 i l (0)*r+L +Uc(0)=E A1=-A2= ()

јас л (т) = ( )

14. Преоден процес во r, L, C – кола кога е поврзан со извор на постојан напон. Критичен процес. Аналитички изрази за i(t), графика. (Класичен метод).

i l (t)=i усни +(B1+B2*t)*

t=0: i l (0)=β1=0

Ако корените се покажат како реални, негативни, еднакви, тогаш процесот е критичен.

15. Преоден процес во r, L, C – кола кога е поврзан со извор на постојан напон. Осцилаторен процес. Аналитички израз за i(t), графика. (Класичен метод).

P t = -δ±j*ω St ω St =

Корените се негативни реални, некои сложени конјугирани.

i l (t)=i уста A1e - δt *sin(ω St t+ψ)

i l (t)=i уста +(M*cos ω светло t+N*sin ω светло t)*

јас л (т) = * = *

16. Преоден процес во r, L, C – кола кога е поврзан со синусоидален извор на напон. Апериодичен процес. Аналитички израз за i(t), графика. (Класичен метод).

R(t)=E max *sin(ωt+ψ)

2.

Во класичниот број на равенки во овој случај е еднаков на бројот на гранки на колото

Методот наоѓа решение во форма на збир на општо и одредено решение. Пресметката на минливиот процес е опишана со систем на обични диференцијални равенки составени со еден од пресметковните методи за моментални вредности на временските функции. Решението за секоја променлива од овој систем се наоѓа во форма на збир на општите и посебните решенија. За да се состави равенка, може да се користи следново: метод заснован на примена на законите на Кирхоф, метод на нодални потенцијали, метод на струи на јамка итн. На пример, систем на диференцијални равенки составен по комутација според првиот и вториот закон на Кирхоф ја има формата:

На пример,

Бројот на равенки во овој случај е еднаков на бројот на гранки на колото. Нека е неопходно да се најде струјата i k во гранка со број K. Елиминирајќи ги струите на гранките во низа, како резултат ја добиваме струјата i k и нејзините деривати до редот n:

Редоследот на диференцијалната равенка n се одредува според бројот на независни реактивни елементи на колото (m). Обично n=m, но во зависност од начинот на поврзување може да биде дека n

Капацитивните елементи поврзани со серија може да се заменат со еден елемент, исто како што паралелно поврзаните индуктивни елементи може да се заменат со еден еквивалентен. Слика 9.5 покажува замена на 2 кондензатори поврзани во серија со еден еквивалентен.

Генерално, редоследот на диференцијалната равенка n е еднаков на: n=n lc -n ce -n lj, каде што n lc е бројот на реактивни елементи (L и C) во колото, n ce е бројот на капацитивните кола, n lj е бројот на индуктивни јазли или пресеци.

Под капацитив се подразбира коло кое се состои од капацитивни елементи или капацитивни елементи и идеални извори на EMF. пресеци кои се вкрстуваат само индуктивни гранки или индуктивни гранки и струјни извори.

Забележете дека фазата на изготвување диференцијална равенка не е задолжителна и дека струјата или напонот на премин може да се најдат без да се изготви равенка. Како што беше наведено, во класичниот метод на пресметување на минливи процеси се решаваат равенките се претставува како збир на општите и посебните решенија.

Посебно решение опишува режим наречен принуден. Решението на хомогена равенка (десната страна е нула) го опишува процесот во отсуство на надворешни EMF и струјни извори и се нарекува слободен. Слободните и присилните струи, напоните и полнењата се разгледуваат соодветно.

Така, струјата во гранката со број К е претставена како збир.

Карактеристичната равенка се составува за колото по префрлувањето. Може да се добие на следниве начини:

Директно врз основа на диференцијална равенка од формата (1.2), т.е. со исклучување од системот на равенки што ја опишуваат електромагнетната состојба на колото врз основа на законите на Кирхоф, сите непознати величини, освен една, во однос на која е напишана равенката;

Со користење на изразот за влезна импеданса на синусоидално струјно коло;

Врз основа на изразот на главната детерминанта.

Според првиот метод во 1.4.1, добиена е диференцијална равенка за напон u Cна кондензаторот за серија r-L-C- синџири (види Сл. 1.6):

врз основа на која се запишува карактеристичната равенка

.

Треба да се забележи дека, бидејќи линеарното коло е покриено со еден преоден процес, корените на карактеристичната равенка се заеднички за сите слободни компоненти на напоните и струите на гранките на колото, чии параметри се вклучени во карактеристичната равенка. Според тоа, според првиот метод на составување на карактеристична равенка, како величина во однос на која е запишана може да се избере која било величина.

Составот на карактеристичната равенка со користење на методот на влезна отпорност е како што следува:

1. Запиши го изразот за влезната отпорност на AC колото во сложена форма;

2. Во добиениот израз jωсе заменува од операторот р;

3. Добиениот израз е еднаков на нула.

Равенката се совпаѓа со карактеристичната.

Треба да се нагласи дека влезниот отпор може да се запише во однос на точката на прекин на која било гранка на колото. Во овој случај, изворите на енергија се исклучени од колото, а нивниот внатрешен отпор останува на нивно место.

Овој метод на составување на карактеристичната равенка претпоставува отсуство на магнетно споени гранки во електричното коло. Доколку ги има, неопходно е да се изврши магнетно раздвојување.

За колото што се разгледува (види Сл. 1.6) користејќи го методот на влезна отпорност имаме:

;

;

.

При составување на карактеристична равенка врз основа на изразот на главната детерминанта, бројот на алгебарски равенки врз основа на кои се пишува е еднаков на бројот на непознати компоненти на слободна струја.

Алгебризацијата на оригиналниот систем на интегро-диференцијални равенки, составена, на пример, врз основа на законите на Кирхоф или методот на контурни струи, се врши со замена на операциите на диференцијација и интеграција, соодветно, со множење и делење од операторот р. Карактеристичната равенка се добива со изедначување на напишаната детерминанта на нула.

Бидејќи изразот за главната детерминанта не зависи од десните страни на системот на нехомогени равенки, тој може да се состави врз основа на систем на равенки напишан за вкупните струи.

За шемата што се разгледува (види Сл. 1.6) за слободен режим имаме:

.

Заменувајќи ги изводот и интегралот во равенката, како што е наведено погоре, ја добиваме алгебарската равенка

или .

Од каде го добиваме?

или .