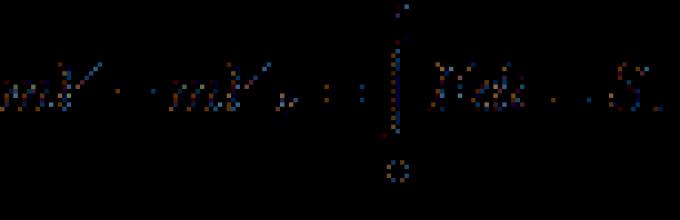Теорема за промена на импулсот на точка. Менување на импулсот на механички систем Закон за промена на импулсот на точка

(Фрагменти од математичка симфонија)

Врската помеѓу импулсот на силата и основната равенка на Њутновата динамика е изразена со теоремата за промена на импулсот на материјална точка.

Теорема.Промената на импулсот на материјалната точка во одреден временски период е еднаква на импулсот на силата () која делува на материјална точкаво истиот временски период.Математичкиот доказ за оваа теорема може да се нарече фрагмент од математичка симфонија. Еве го.

Диференцијалниот импулс на материјалната точка е еднаков на елементарниот импулс на силата што дејствува на материјалната точка. Интегрирајќи го изразот (128) за диференцијалниот импулс на материјална точка, имаме

(129)

Теоремата е докажана и математичарите сметаат дека нивната мисија е завршена, но инженерите, чија судбина е свето да веруваат во математичарите, имаат прашања кога ја користат докажаната равенка (129). Но, тие се цврсто блокирани од редоследот и убавината на математичките операции (128 и 129), кои фасцинираат и нè поттикнуваат да ги наречеме фрагмент од математичка симфонија. Колку генерации инженери се согласија со математичарите и беа воодушевени од мистеријата на нивните математички симболи! Но, тогаш имаше инженер кој не се согласуваше со математичарите и им поставуваше прашања.

Почитувани математичари!Зошто ниту еден од вашите учебници за теоретска механика не го дискутира процесот на примена на вашиот симфониски резултат (129) во пракса, на пример, кога го опишувате процесот на забрзување на автомобилот? Левата страна на равенката (129) е многу јасна. Автомобилот го започнува забрзувањето од брзина и го завршува, на пример, со брзина. Сосема е природно равенката (129) да стане

И веднаш се поставува првото прашање: како можеме од равенката (130) да ја одредиме силата под чие влијание автомобилот се забрзува до брзина од 10 m/s? Одговорот на ова прашање го нема во ниту еден од безбројните учебници по теоретска механика. Ајде да одиме понатаму. По забрзувањето, автомобилот почнува да се движи рамномерно со брзина од 10 m/s. Која сила ја движи колата?????????? Немам друг избор освен да поцрвенам заедно со математичарите. Првиот закон на Њутновата динамика вели дека кога автомобилот се движи рамномерно, на него не дејствуваат никакви сили, а автомобилот, фигуративно кажано, кива на овој закон, троши бензин и работи, движејќи се, на пример, на растојание од 100 km. Каде е силата што работеше да го помести автомобилот 100 km? Симфониската математичка равенка (130) молчи, но животот продолжува и бара одговор. Почнуваме да го бараме.

Бидејќи автомобилот се движи праволиниски и рамномерно, силата што ја придвижува е константна по големина и насока и равенката (130) станува

(131)

Значи, равенката (131) во овој случај го опишува забрзаното движење на телото. На што е еднаква силата? Како да се изрази нејзината промена со текот на времето? Математичарите претпочитаат да го заобиколат ова прашање и да го препуштат на инженерите, верувајќи дека тие мора да го бараат одговорот на ова прашање. На инженерите им останува една опција - да се земе предвид дека ако по завршувањето на забрзаното движење на телото, започнува фаза на еднообразно движење, која е придружена со дејството постојана силасегашната равенка (131) за моментот на премин од забрзано во еднообразно движење во оваа форма

(132)

Стрелката во оваа равенка не го означува резултатот од интегрирањето на оваа равенка, туку процесот на премин од нејзината интегрална форма во поедноставена форма. Силата во оваа равенка е еквивалентна на просечната сила што го променила моментумот на телото од нула до конечна вредност. Значи, драги математичари и теоретски физичари, отсуството на вашиот метод за одредување на големината на вашиот импулс нè принудува да ја поедноставиме постапката за одредување сила, а отсуството на метод за одредување на времето на дејство на оваа сила генерално не става во безизлезна положба и ние сме принудени да користиме израз за да го анализираме процесот на промена на импулсот на телото. Резултатот е дека колку подолго дејствува силата, толку е поголем нејзиниот импулс. Ова јасно е во спротивност со одамна воспоставената идеја дека колку е пократко времетраењето на неговото дејство, толку е поголем импулсот на силата.

Да обрнеме внимание на фактот дека промената на импулсот на материјалната точка (импулсот на сила) за време на нејзиното забрзано движење се случува под дејство на Њутнова сила и сили на отпорност на движење, во форма на сили генерирани од механички отпори и силата на инерција. Но, Њутновата динамика во огромното мнозинство на проблеми ја игнорира силата на инерција, а Механодинамиката наведува дека промената на импулсот на телото за време на неговото забрзано движење се јавува поради вишокот на Њутновата сила над силите на отпорност на движење, вклучително и сила на инерција.

Кога телото се движи во бавно движење, на пример, автомобил со исклучен менувач, нема Њутнова сила, а промената на моментумот на автомобилот се јавува поради вишокот на силите на отпор на движење над силата на инерција, која го движи автомобилот кога се движи бавно.

Како сега можеме да ги вратиме резултатите од забележаните „симфониски“ математички дејства (128) во главниот тек на причинско-последичните врски? Има само еден излез - да се најде нова дефиниција на концептите „импулс на сила“ и „сила на удар“. За да го направите ова, поделете ги двете страни на равенката (132) со времето t. Како резултат ќе имаме

. (133)

Да забележиме дека изразот mV/t е брзина на промена на импулсот (mV/t) на материјална точка или тело. Ако се земе предвид дека V/t е забрзување, тогаш mV/t е силата што го менува моментумот на телото. Истата димензија лево и десно од знакот за еднакво ни дава право да ја наречеме силата F ударна сила и да ја означиме со симболот, а импулсот S - ударен импулс и да ја означиме со симболот. Ова води до нова дефиниција за силата на ударот. Силата на ударот што дејствува на материјална точка или тело е еднаква на односот на промената на моментумот на материјалната точка или телото до времето на оваа промена.

Да обрнеме посебно внимание на фактот дека само Њутновата сила учествува во формирањето на ударниот импулс (134), кој ја промени брзината на автомобилот од нулта вредностдо максимум - , затоа равенката (134) целосно припаѓа на Њутновата динамика. Бидејќи е многу полесно експериментално да се одреди големината на брзината отколку да се одреди забрзувањето, формулата (134) е многу погодна за пресметки.

Овој необичен резултат произлегува од равенката (134).

Да обрнеме внимание на фактот дека според новите закони на механодинамиката, генератор на импулсот на сила при забрзано движење на материјална точка или тело е Њутновата сила. Тој го формира забрзувањето на движењето на точка или тело, при што автоматски се јавува инерцијална сила, насочена спротивно на Њутновата сила и ударот Њутновата сила мора да го надмине дејството на инерцијалната сила, затоа инерцијалната сила мора да биде претставена во рамнотежа на силите на левата страна од равенката (134). Бидејќи инерцијалната сила е еднаква на масата на точката или телото помножена со забавувањето што го формира, тогаш равенката (134) станува

(136)

Почитувани математичари!Погледнете во каква форма беше математички модел, опишувајќи го ударниот импулс, кој го забрзува движењето на ударното тело од нулта брзина до максималната V (11). Сега да ја провериме неговата работа во одредувањето на ударниот импулс, кој е еднаков на силата на ударот што ја запали втората енергетска единица на SShG (сл. 120), и ќе ве оставиме со вашата бескорисна равенка (132). За да не ја комплицираме презентацијата, формулата (134) засега ќе ја оставиме сама и ќе користиме формули кои даваат просечни вредности на силите. Гледаш на која позиција ставаш инженер кој се обидува да реши конкретен проблем.

Да почнеме со Њутнова динамика. Експертите откриле дека втората енергетска единица се искачила на висина од 14 m. Бидејќи се издигнал во гравитационото поле, тогаш на висина од h=14m тој потенцијална енергијаиспадна дека е еднакво

а просечната кинетичка енергија била еднаква на

Ориз. 120. Фотографија од просторијата за турбина пред катастрофата

Од еднаквоста на кинетичката (138) и потенцијалната (137) енергија, следи просечната стапка на пораст на енергетската единица (сл. 121, 122)

Ориз. 121. Фотон на турбинската просторија по катастрофата

Според новите закони на механодинамиката, издигнувањето на енергетската единица се состоеше од две фази (сл. 123): првата фаза ОА - забрзан пораст и втората фаза AB - бавен пораст , , .

Времето и растојанието на нивното дејство се приближно еднакви (). Тогаш кинематската равенка на забрзаната фаза на подигање на енергетската единица ќе биде напишана на следниов начин:

. (140)

Ориз. 122. Поглед на бунарот на енергетската единица и самата енергетска единица по катастрофата

Законот за промена на стапката на пораст на енергетската единица во првата фаза има форма

. (141)

Ориз. 123. Редовност на промените на брзината на летот V на енергетска единица

Заменувајќи го времето од равенката (140) во равенката (141), имаме

. (142)

Времето на подигнување на блокот во првата фаза се одредува според формулата (140)

. (143)

Тогаш вкупното време за подигање на енергетската единица на висина од 14 m ќе биде еднакво на . Масата на енергетската единица и капакот е 2580 тони. Според Њутновата динамика, силата што ја подигнала енергетската единица е еднаква на

Почитувани математичари!Ги следиме вашите симфониски математички резултати и ја запишуваме вашата формула (129), следејќи ја Њутновата динамика, за да го одредиме ударниот пулс што ја активирал втората енергетска единица

и поставете основно прашање: како да го одредите времетраењето на ударниот пулс што ја запали 2-та енергетска единица?????????????

Мил!!!Запомнете колку креда напишаа на таблите генерации ваши колеги, апструзно учејќи ги учениците како да го одредат ударниот импулс, а никој не објасни како да се одреди времетраењето на ударниот импулс во секој конкретен случај. Ќе кажете дека времетраењето на ударниот импулс е еднакво на временскиот интервал на промената на брзината на енергетската единица од нула до, ќе претпоставиме, максимална вредност од 16,75 m/s (139). Таа е во формулата (143) и е еднаква на 0,84 с. Засега се согласуваме со вас и ја одредуваме просечната вредност на ударниот импулс

Веднаш се поставува прашањето: зошто големината на ударниот импулс (146) е помала од Њутновата сила од 50600 тони? Вие, драги математичари, немате одговор. Ајде да одиме понатаму.

Според Њутновата динамика, главната сила, кој се спротивстави на подемот на енергетската единица, е силата на гравитацијата. Бидејќи оваа сила е насочена против движењето на енергетската единица, таа генерира забавување, што е еднакво на забрзување слободен пад. Тогаш гравитационата сила што дејствува на енергетската единица која лета нагоре е еднаква на

Њутновата динамика не ги зема предвид другите сили кои го спречија дејството на Њутновата сила од 50.600 тони (144), а механодинамиката наведува дека на подемот на енергетската единица исто така му се спротивставила инерцијална сила еднаква на

Веднаш се поставува прашањето: како да се најде количината на забавување во движењето на енергетската единица? Њутновата динамика молчи, но механодинамиката одговара: во моментот на дејствување на Њутновата сила, која ја подигнала енергетската единица, ѝ се спротивставиле: силата на гравитација и силата на инерција, па затоа равенката на силите што делуваат на моќта единица во тој момент се пишува на следниов начин.

Мерка за количина на движење механичко движење, ако механичкото движење премине во механичко. На пример, механичкото движење на топката за билијард (сл. 22) пред ударот се претвора во механичко движење на топчињата по ударот. За точка, моментумот е еднаков на производот.

Мерката на силата во овој случај е импулсот на силата

. (9.1)

Моментумот го одредува дејството на силата во текот на одреден временски период . За материјална точка, теоремата за промена на импулсот може да се користи во диференцијална форма
(9.2) или интегрална (конечна) форма
. (9.3)

Промената на моментумот на материјална точка во одреден временски период е еднаква на импулсот на сите сили што се применуваат на точката во исто време.

Слика 22

При решавање проблеми, теоремата (9.3) почесто се користи во проекции на координатни оски
;

; (9.4)

.

Користејќи ја теоремата за промената на импулсот на точката, можно е да се решат проблеми во кои на точка или тело што се движи транслативно се делува со постојани или променливи сили кои зависат од времето, а дадените и бараните величини го вклучуваат времето на движење и брзини на почетокот и на крајот на движењето. Задачите со користење на теоремата се решаваат во следната низа:

1. изберете координатен систем;

2. ги прикажува сите дадени (активни) сили и реакции кои дејствуваат на точка;

3. запиши теорема за промената на импулсот на точка во проекциите на избраните координатни оски;

4. определување на потребните количини.

ПРИМЕР 12.

Чекан со тежина G=2t паѓа од височина h=1m на работното парче во време t=0,01s и го печат делот (сл. 23). Определете ја просечната сила на притисок на чеканот на работното парче.

РЕШЕНИЕ.

1. Работното парче е предмет на силата на гравитацијата на чеканот и реакција на земјата . Големината на реакцијата на поддршка се менува со текот на времето, па да ја разгледаме нејзината просечна вредност
.

2. насочете ја координатната оска y вертикално надолу и применете ја теоремата за промената на импулсот на точка во проекцијата на оваа оска:
, (1) каде -- брзина на чекан на крајот на ударот;

-- почетна брзина на чеканот во моментот на допир со работното парче.

3. За да се одреди брзината ајде да се нашминкаме диференцијална равенкадвижење на чекан во проекција на y-оската:

. (2)

Да ги одделиме променливите и да ја интегрираме равенката (2) двапати:
;

;

. Ги наоѓаме интеграциските константи C 1, C 2 од почетните услови. На t=0 V y =0, тогаш C 1 =0; y=0, потоа C 2 =0. Затоа, чеканот се движи според законот
, (3) и брзината на чеканот се менува според закон
. (4) Да го изразиме времето на движење на чеканот од (3) и да го замениме со (4)
;
. (5)

4. Ја наоѓаме проекцијата на импулсот на надворешните сили на y-оската со помош на формулата:
. (6) Заменете ги (5) и (6) во (1):
, од каде ја наоѓаме реакцијата на потпорот и, следствено, саканиот притисок на чеканот на работното парче
Т.

Слика 24

ДО

каде M е масата на системот, V c е брзината центар на маса. Теоремата за промена на импулсот на механички систем може да се напише во диференцијална и конечна (интегрална) форма:
;

. (9.7)

Количината на движење на механички систем може да се дефинира како збир на количините на движење на точките на системот
. (9.5) Импулсот на систем или круто тело може да се одреди со познавање на масата на системот и брзината на центарот на маса
, (9.6)

Промената на моментумот на механичкиот систем во одреден временски период е еднаква на збирот на импулсите на надворешните сили кои дејствуваат во исто време. Понекогаш е попогодно да се користи теоремата за промената на импулсот во проекцијата на координатните оски
; (9.8)
. (9.9)

Законот за зачувување на импулсот вели дека во отсуство на надворешни сили, моментумот на механичкиот систем останува константен. Акција внатрешните силине може да го промени моментумот на системот. Од равенката (9.6) е јасно дека кога
,
.

Ако
, Тоа
или
.

Д

пропелер или пропелер, млазен погон. Лигњите се движат во грчи, исфрлајќи вода од мускулестата кеса како воден топ (сл. 25). Отфрлената вода има одредена количина на движење насочено наназад. Лигњите ја добиваат соодветната брзина движење напред поради реактивна влечна сила , бидејќи пред лигњите да искокнат од силата избалансиран со гравитација .

Ефектот на законот за зачувување на импулсот на механичкиот систем може да се илустрира со примерот на феноменот на одвраќање или враќање назад при пукање, работа

Примената на теоремата за промена на импулсот ни овозможува да ги исклучиме сите внатрешни сили од разгледување.

ПРИМЕР 13.

Винч А со барабан со радиус r е инсталиран на железничка платформа слободно стои на шините (сл. 26). Винчот е дизајниран да поместува товар B со маса m 1 долж платформата. Тежина на платформата со крик m 2. Тапанот на винчот се ротира според законот
. Во почетниот момент системот беше подвижен. Занемарувајќи го триењето, пронајдете го законот за промена на брзината на платформата откако ќе го вклучите крилото.

Р РЕШЕНИЕ.

1. Размислете за платформата, крилото и оптоварувањето како единствен механички систем, кој е предмет на надворешни сили: гравитација на оптоварување и платформи и реакции И
.

2. Бидејќи сите надворешни сили се нормални на оската x, т.е.
, го применуваме законот за зачувување на импулсот на механички систем при проекција на оската x:
. Во почетниот момент системот бил неподвижен, затоа,

Да ја изразиме количината на движење на системот во произволен момент во времето. Платформата се движи напред со брзина , товарот се подложува на сложено движење кое се состои од релативно движење по платформата со брзина и преносливо движење заедно со платформата со брзина ., каде
. Платформата ќе се движи во насока спротивна на релативното движење на товарот.

ПРИМЕР 14.

М

РЕШЕНИЕ.

1. Да ја примениме теоремата за промената на импулсот на механички систем при проекција на оската x. Бидејќи сите надворешни сили кои делуваат на системот се вертикални, тогаш
, Потоа
, каде
. (1)

2. Да ја изразиме проекцијата на импулсот на оската x за механичкиот систем што се разгледува
,

Механичкиот систем се состои од правоаголна вертикална плоча 1 со маса m 1 = 18 kg, која се движи по хоризонтални водилки и товар D со маса m 2 = 6 kg. Во моментот на t 0 =0, кога плочата се движела со брзина u 0 =2m/s, товарот почнал да се движи по ровот во согласност со равенката S=AD=0.4sin( t 2) (S-во метри, t-во секунди), (сл. 26). Да се ​​определи брзината на плочата во време t 1 = 1s, користејќи ја теоремата за промена на импулсот на механички систем.

Каде ,
-- количината на движење на плочата и оптоварувањето, соодветно.

;
, Каде --апсолутна брзина на товарот Д. Од еднаквоста (1) следува дека K 1x + K 2x =C 1 или m 1 u x +m 2 V Dx =C 1. (2) За да се одреди V Dx, сметајте го движењето на товарот D како сложено, земајќи го предвид неговото движење во однос на плочата релативно, а движењето на самата плоча преносливо, тогаш
, (3)
;или во проекција на оската x: . (4) Да го замениме (4) во (2):
. (5) Константата на интеграција C 1 ја одредуваме од почетните услови: при t=0 u=u 0 ; (m 1 + m 2) u 0 = C 1. (6) Заменувајќи ја вредноста на константата C 1 во равенката (5), добиваме

Госпоѓица.

За материјална точка, основниот закон на динамиката може да се претстави како

Помножувајќи ги двете страни на оваа релација лево векторски со векторот на радиусот (сл. 3.9), добиваме

(3.32)

На десната страна од оваа формула го имаме моментот на сила во однос на точката О. Ја трансформираме левата страна со примена на формулата за изводот на векторски производ

Но Како векторски производпаралелни вектори. По ова добиваме

(3.33)

Првиот извод во однос на времето на моментот на моментот на точка во однос на кој било центар е еднаков на моментот на сила во однос на истиот центар.

Пример за пресметување на аголниот моментум на систем. Пресметајте го кинетичкиот момент во однос на точката O на систем кој се состои од цилиндрично вратило со маса M = 20 kg и радиус R = 0,5 m и опаѓачко оптоварување со маса m = 60 kg (Слика 3.12). Оската се ротира околу оската Оз со аголна брзина ω = 10 s -1.

Слика 3.12

; ;

За дадени влезни податоци, аголниот моментум на системот

Теорема за промената на аголниот моментум на системот.Ние ги применуваме резултантните надворешни и внатрешни сили на секоја точка од системот. За секоја точка од системот, можете да ја примените теоремата за промената на аголниот моментум, на пример во формата (3.33)

Сумирајќи ги сите точки на системот и земајќи предвид дека збирот на изводите е еднаков на изводот на збирот, добиваме

Со определување на кинетичкиот момент на системот и својствата на надворешните и внатрешните сили

Затоа, добиената врска може да се претстави како

Првиот патен дериват на аголниот моментум на системот во однос на која било точка е еднаков на главниот момент на надворешните сили кои делуваат на системот во однос на истата точка.

3.3.5. Работа на сила

1) Елементарната работа на силата е еднаква на скаларниот производ на силата и диференцијалниот радиус на векторот на точката на примена на силата (сл. 3.13)

Слика 3.13

Изразот (3.36) може да се запише и во следните еквивалентни форми

каде е проекцијата на силата на правецот на брзината на точката на примена на силата.

2) Работа на сила при конечно поместување

Интегрирајќи ја елементарната работа на сила, ги добиваме следните изрази за работа на сила при конечно поместување од точка А до точка Б

3) Работа со постојана сила

Ако силата е константна, тогаш од (3.38) следи

Работата на константна сила не зависи од обликот на траекторијата, туку зависи само од векторот на поместување на точката на примена на силата.

4) Работа на тежинска сила

За тежинската сила (сл. 3.14) и од (3.39) добиваме

Слика 3.14

Ако движењето се случи од точката Б до точката А, тогаш

Генерално

Знакот „+“ одговара на надолното движење на точката на примена на сила, знакот „-“ - нагоре.

4) Работа на еластична сила

Нека оската на пружината е насочена по оската x (сл. 3.15), а крајот на пружината се движи од точката 1 до точката 2, а потоа од (3.38) добиваме

Ако вкочанетоста на пружината е Со, па тогаш

А (3.41)

Ако крајот на пружината се помести од точката 0 до точката 1, тогаш во овој израз го заменуваме , , тогаш работата на еластичната сила ќе добие форма

(3.42)

каде е издолжувањето на изворот.

Слика 3.15

5) Работата на силата што се применува на ротирачко тело. Делото на моментот.

На сл. Слика 3.16 покажува ротирачко тело на кое се применува произволна сила. За време на ротацијата, точката на примена на оваа сила се движи во круг.

Нека материјалната точка се движи под влијание на сила Ф. Потребно е да се одреди движењето на оваа точка во однос на подвижниот систем Оксиз(види сложено движење на материјална точка), која се движи на познат начин во однос на стационарен систем О 1 x 1 y 1 z 1 .

Основна равенка на динамиката во стационарен систем

Дозволете ни да го запишеме апсолутното забрзување на точка користејќи ја теоремата Кориолисова

Каде а стомачни мускули– апсолутно забрзување;

а однос– релативно забрзување;

а лента– преносливо забрзување;

а јадро– Кориолисово забрзување.

Ајде да го преработиме (25) земајќи го предвид (26)

Да ја воведеме ознаката
- пренослива сила на инерција,
- Кориолисова инерцијална сила. Тогаш равенката (27) добива форма

Основната равенка на динамиката за проучување на релативното движење (28) е напишана на ист начин како и за апсолутното движење, само на силите што дејствуваат на точката мора да се додадат силите на пренос и Кориолисовата инерција.

Општи теореми за динамиката на материјална точка

Кога решавате многу проблеми, можете да користите претходно направени празни места добиени врз основа на вториот закон на Њутн. Ваквите методи за решавање проблеми се комбинирани во овој дел.

Теорема за промена на импулсот на материјална точка

Да ги претставиме следните динамички карактеристики:

1. Моментум на материјална точка – векторска количина, еднаков на производот од масата на точката и нејзиниот вектор на брзина

. (29)

2. Присилете импулс

Елементарен импулс на сила– векторска количина еднаква на производот на векторот на сила и елементарен временски интервал

(30).

Потоа полн импулс

. (31)

На Ф=постојано добиваме С=Ft.

Вкупниот импулс за конечен временски период може да се пресмета само во два случаи, кога силата што дејствува на точка е константна или зависи од времето. Во други случаи, неопходно е да се изрази силата во функција на времето.

Еднаквоста на димензиите на импулсот (29) и моментумот (30) ни овозможува да воспоставиме квантитативна врска меѓу нив.

Да го разгледаме движењето на материјалната точка М под дејство на произволна сила Фпо произволна траекторија.

ЗА UD:
. (32)

Ги издвојуваме променливите во (32) и интегрираме

. (33)

Како резултат на тоа, земајќи ја предвид (31), добиваме

. (34)

Равенката (34) ја изразува следната теорема.

Теорема: Промената на моментумот на материјалната точка во одреден временски период е еднаква на импулсот на силата што делува на точката во истиот временски интервал.

При решавање проблеми, равенката (34) мора да се проектира на координатните оски

Оваа теорема е погодна за употреба кога меѓу дадените и непознатите величини има масата на точката, нејзината почетна и конечна брзина, сили и време на движење.

Теорема за промена на аголниот моментум на материјална точка

М
момент на импулс на материјална точкаво однос на центарот е еднаков на производот на модулот на моментумот на точката и рамото, т.е. најкраткото растојание (нормално) од центарот до линијата што се совпаѓа со вектор на брзина

, (36)

. (37)

Односот помеѓу моментот на сила (причина) и моментот на моментумот (ефект) се утврдува со следнава теорема.

Нека точка М од дадена маса мсе движи под влијание на сила Ф.

,
,

, (38)

. (39)

Да го пресметаме изводот на (39)

. (40)

Комбинирајќи ги (40) и (38), конечно добиваме

. (41)

Равенката (41) ја изразува следната теорема.

Теорема: Временскиот дериват на векторот на аголниот моментум на материјална точка во однос на одреден центар е еднаков на моментот на силата што дејствува на точката во однос на истиот центар.

При решавање на проблеми, равенката (41) мора да се проектира на координатните оски

Во равенките (42), моментите на импулсот и силата се пресметуваат во однос на координатните оски.

Од (41) следува закон за зачувување на аголниот моментум (Кеплеровиот закон).

Ако моментот на сила што дејствува на материјална точка во однос на кој било центар е нула, тогаш аголниот моментум на точката во однос на овој центар ја задржува својата големина и насока.

Ако
, Тоа
.

Теоремата и законот за зачувување се користат во проблеми кои вклучуваат кривилинеарно движење, особено под дејство на централните сили.

Количината на движење на системот, како векторска величина, се одредува со формулите (4.12) и (4.13).

Теорема. Дериватот на моментумот на системот во однос на времето е еднаков на геометрискиот збир на сите надворешни сили што дејствуваат на него.

Во проекциите на Декартовските оски добиваме скаларни равенки.

Можете да напишете вектор

(4.28)

и скаларни равенки

Кои ја изразуваат теоремата за промената на импулсот на системот во интегрална форма: промената на моментумот на системот во одреден временски период е еднаква на збирот на импулсите во истиот временски период. При решавање проблеми почесто се користат равенките (4.27).

Закон за зачувување на моментумот

Теорема за промена на аголниот моментум

Теоремата за промена на аголниот импулс на точка во однос на центарот: временскиот извод на аголниот моментум на точка во однос на фиксен центар е еднаков на векторскиот момент на сила што дејствува на точката во однос на истиот центар.

Или (4.30)

Споредувајќи ги (4.23) и (4.30), гледаме дека моментите на векторите и се поврзани со иста зависност како и векторите и самите тие се поврзани (сл. 4.1). Ако проектираме еднаквост на оската што минува низ центарот О, добиваме

(4.31)

Оваа еднаквост ја изразува теоремата на аголниот момент на точка во однос на оската.

Ориз. 4.1.

Теоремата за промената на главниот аголен момент или аголниот момент на механички систем во однос на центарот: временскиот дериват на кинетичкиот аголен момент на системот во однос на одреден фиксен центар е еднаков на збирот на моментите на сите надворешни сили во однос на истиот центар.

(4.32)

Ако го проектираме изразот (4.32) на оската што минува низ центарот O, ќе добиеме еднаквост што ја карактеризира теоремата за промената на аголниот моментум во однос на оската.

(4.33)

Заменувајќи го (4.10) во еднаквост (4.33), можеме да ја запишеме диференцијалната равенка на ротирачкото круто тело (тркала, оски, вратила, ротори итн.) во три форми.

(4.34)

(4.35)

(4.36)

Така, препорачливо е да се користи теоремата за промена на кинетичкиот момент за проучување на движењето на круто тело, што е многу вообичаено во технологијата, неговата ротација околу фиксна оска.

Закон за зачувување на аголниот моментум на системот

1. Нека во изразот (4.32) .

Тогаш од равенката (4.32) произлегува дека, т.е. ако збирот на моментите на сите надворешни сили што се применуваат на системот во однос на даден центар е еднаков на нула, тогаш кинетичкиот момент на системот во однос на овој центар ќе биде нумерички и насочен константен.

2. Ако , тогаш . Така, ако збирот на моментите на надворешните сили кои делуваат на системот во однос на одредена оска е нула, тогаш кинетичкиот момент на системот во однос на оваа оска ќе биде константна вредност.

Овие резултати го изразуваат законот за зачувување на аголниот моментум.

Во случај на ротирачко круто тело, од еднаквоста (4.34) следи дека, ако , тогаш . Од тука доаѓаме до следните заклучоци:

Ако системот е непроменлив (апсолутно солидна), тогаш, според тоа, и крутото тело ротира околу фиксна оска со постојана аголна брзина.

Ако системот е променлив, тогаш . Со зголемување (тогаш поединечните елементи на системот се оддалечуваат од оската на ротација), аголната брзина се намалува, бидејќи , а при намалување се зголемува, така што кај променлив систем со помош на внатрешни сили е можно да се смени аголната брзина.

Втора задача Д2 тест работае посветен на теоремата за промената на аголниот моментум на системот во однос на оската.

Задача Д2

Хомогена хоризонтална платформа (кружна со радиус R или правоаголна со страни R и 2R, каде што R = 1,2 m) со маса од kg ротира со аголна брзина околу вертикалната оска z, оддалечена од центарот на масата C на платформата на растојание OC = b (сл. E2.0 – D2.9, табела D2); Димензиите за сите правоаголни платформи се прикажани на сл. D2.0a (горен поглед).

Во моментот, товарот D со маса од kg почнува да се движи по должината на платформата (под влијание на внатрешните сили) според законот, каде што s се изразува во метри, t - во секунди. Во исто време, пар сили со момент М (наведен во њутнометри; во М< 0 его направление противоположно показанному на рисунках).

Определете, занемарувајќи ја масата на вратилото, зависноста т.е. аголна брзина на платформата во функција на времето.

На сите слики, оптоварувањето D е прикажано во позиција во која s > 0 (кога s< 0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на дадено растојание OC = b од центарот C.

Правци.Задача Д2 – да се примени теоремата за промената на аголниот моментум на системот. При примена на теоремата на систем кој се состои од платформа и оптоварување, аголниот момент на системот во однос на оската z се одредува како збир на моментите на платформата и оптоварувањето. Треба да се земе предвид дека апсолутната брзина на оптоварувањето е збир на релативните и преносливите брзини, т.е. . Затоа, количината на движење на овој товар . Потоа можете да ја користите теоремата на Варињон (статика), според која; овие моменти се пресметуваат на ист начин како моментите на силите. Решението е подетално објаснето во примерот Д2.

Кога решавате проблем, корисно е да се прикаже во помошен цртеж поглед на платформата одозгора (од крајот z), како што е направено на сл. Д2.0, а – Д2.9, а.

Моментот на инерција на плоча со маса m во однос на оската Cz, нормално на плочата и минува низ нејзиниот центар на маса, е еднаков на: за правоаголна плоча со страни и

;

За тркалезна плоча со радиус R

Број на состојба	б	s = F(t)	М
	R R/2 R R/2 R R/2 R R/2 R R/2	-0,4 0,6 0,8 10 t 0,4 -0,5t -0,6t 0,8t 0,4 0,5	4t -6 -8t -9 6 -10 12

	Ориз. D2.0		Ориз. D2.0a

	Ориз. D2.1		Ориз. D2.1a

	Ориз. D2.2		Ориз. Д2.2а

	Ориз. D2.3		Ориз. D2.3a

	Ориз. D2.4
		Ориз. D2.4a

		Ориз. D2.5a
	Ориз. Д2.5

	Ориз. D2.6		Ориз. D2.6a

	Ориз. D2.7		Ориз. D2.7a

	Ориз. D2.8		Ориз. D2.8a

	Ориз. D2.9		Ориз. D2.9a

	Ориз. Д 2

Пример Д2. Хомогена хоризонтална платформа (правоаголна со страни 2l и l), која има маса, е цврсто прикачена на вертикално вратило и се ротира со неа околу оската zсо аголна брзина (сл. E2a ). Во моментот, вртежниот момент М почнува да дејствува на вратилото, насочен спротивно ; истовремено товар Дмаса лоцирана во ровот АБво точката СО,почнува да се движи по шахтата (под влијание на внатрешните сили) според законот s = CD = F(t).

Дадени: m 1 = 16 kg, т 2= 10 кг, л= 0,5 m, = 2, s = 0,4t 2 (s - во метри, t - во секунди), М= kt,Каде к=6 Nm/s. Дефинирај: - закон за промена аголна брзинаплатформи.

Решение.Размислете за механички систем кој се состои од платформа и товар Д.За да го одредиме w, ја применуваме теоремата за промената на аголниот момент на системот во однос на оската z:

(1)

Дозволете ни да ги прикажеме надворешните сили што дејствуваат на системот: гравитационата сила на реакцијата и вртежниот момент M. Бидејќи силите и се паралелни на оската z, а реакциите ја сечат оваа оска, нивните моменти во однос на оската z се еднакви на нула. Потоа, земајќи ја предвид насоката за моментот да биде позитивна (т.е. спротивно од стрелките на часовникот), добиваме а равенката (1) ќе ја добие оваа форма.