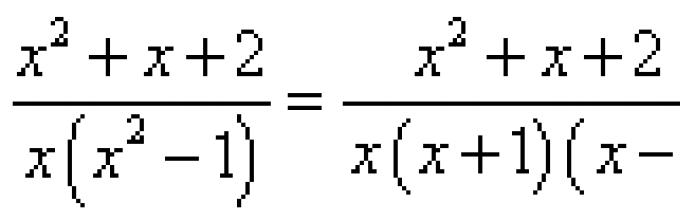Рационална функција е дропка од формата чиј броител и именител се полиноми или производи на полиноми.

Пример 1. Чекор 2.

.

Неодредените коефициенти ги множиме со полиноми кои не се во оваа поединечна дропка, но кои се во други добиени дропки:

Ги отвораме заградите и го изедначуваме броителот на оригиналниот интегранд со добиениот израз:

Во двете страни на еднаквоста, бараме членови со исти моќи на x и составуваме систем на равенки од нив:

.

Ги поништуваме сите x и добиваме еквивалентен систем на равенки:

.

Така, конечното проширување на интеграндот во збир на едноставни дропки е:

.

Пример 2. Чекор 2.На чекор 1, го добивме следното распаѓање на првобитната дропка во збир на едноставни дропки со неодредени коефициенти во броителите:

.

Сега почнуваме да бараме неизвесни коефициенти. За да го направите ова, го изедначуваме броителот на првобитната дропка во изразот на функцијата со броителот на изразот добиен по намалувањето на збирот на дропки на заеднички именител:

Сега треба да креирате и решите систем на равенки. За да го направите ова, ги изедначуваме коефициентите на променливата до соодветниот степен во броителот на оригиналниот израз на функцијата и слични коефициенти во изразот добиен на претходниот чекор:

Го решаваме добиениот систем:

Значи, од тука

.

Пример 3. Чекор 2.На чекор 1, го добивме следното распаѓање на првобитната дропка во збир на едноставни дропки со неодредени коефициенти во броителите:

Почнуваме да бараме неизвесни коефициенти. За да го направите ова, го изедначуваме броителот на првобитната дропка во изразот на функцијата со броителот на изразот добиен по намалувањето на збирот на дропки на заеднички именител:

Како и во претходните примери, составуваме систем на равенки:

Ги намалуваме х-овите и добиваме еквивалентен систем на равенки:

Решавајќи го системот, ги добиваме следните вредности на неизвесните коефициенти:

Го добиваме конечното разложување на интеграндот во збир на едноставни дропки:

.

Пример 4. Чекор 2.На чекор 1, го добивме следното распаѓање на првобитната дропка во збир на едноставни дропки со неодредени коефициенти во броителите:

.

Од претходните примери веќе знаеме како да се изедначи броителот на првобитната дропка со изразот во броителот добиен по разложување на дропката во збир на едноставни дропки и доведување на оваа сума до заеднички именител. Затоа, само за контролни цели, го прикажуваме добиениот систем на равенки:

Решавајќи го системот, ги добиваме следните вредности на неизвесните коефициенти:

Го добиваме конечното разложување на интеграндот во збир на едноставни дропки:

Пример 5. Чекор 2.На чекор 1, го добивме следното распаѓање на првобитната дропка во збир на едноставни дропки со неодредени коефициенти во броителите:

.

Ние независно ја намалуваме оваа сума на заеднички именител, изедначувајќи го броителот на овој израз со броителот на првобитната дропка. Резултатот треба да биде следниов систем на равенки:

Решавајќи го системот, ги добиваме следните вредности на неизвесните коефициенти:

.

Го добиваме конечното разложување на интеграндот во збир на едноставни дропки:

.

Пример 6. Чекор 2.На чекор 1, го добивме следното распаѓање на првобитната дропка во збир на едноставни дропки со неодредени коефициенти во броителите:

Со оваа сума ги извршуваме истите дејства како и во претходните примери. Резултатот треба да биде следниов систем на равенки:

Решавајќи го системот, ги добиваме следните вредности на неизвесните коефициенти:

.

Го добиваме конечното разложување на интеграндот во збир на едноставни дропки:

.

Пример 7. Чекор 2.На чекор 1, го добивме следното распаѓање на првобитната дропка во збир на едноставни дропки со неодредени коефициенти во броителите:

.

По одредени дејства со добиениот износ, треба да се добие следниот систем на равенки:

Решавајќи го системот, ги добиваме следните вредности на неизвесните коефициенти:

Го добиваме конечното разложување на интеграндот во збир на едноставни дропки:

.

Пример 8. Чекор 2.На чекор 1, го добивме следното распаѓање на првобитната дропка во збир на едноставни дропки со неодредени коефициенти во броителите:

.

Ајде да направиме некои промени во дејствата што веќе се доведени до автоматичност за да добиеме систем на равенки. Постои вештачка техника која во некои случаи помага да се избегнат непотребните пресметки. Донесувајќи го збирот на дропки до заеднички именител, добиваме и изедначувајќи го броителот на овој израз со броителот на првобитната дропка, добиваме.

Методот е применлив за минимизирање на функциите на логичката алгебра на кој било број на променливи.

Да го разгледаме случајот со три променливи. Буловата функција во DNF може да се претстави во форма на сите видови конјунктивни термини кои можат да бидат вклучени во DNF:

каде kО(0,1) се коефициенти. Методот се состои во избор на коефициенти на таков начин што добиениот DNF е минимален.

Ако сега ги поставиме сите можни вредности на променливите од 000 до 111, добиваме 2 n (2 3 = 8) равенки за одредување на коефициентите к:

Со оглед на множествата за кои функцијата зема нулта вредност, определи ги коефициентите кои се еднакви на 0 и пречкртај ги од равенките чија десна страна содржи 1. Од преостанатите коефициенти во секоја равенка, еден коефициент се изедначува со еден, што одредува сврзникот од најнискиот ранг. Останатите коефициенти се еднакви на 0. Значи, единечните коефициенти кодреди соодветна минимална форма.

Пример. Минимизирајте дадена функција

ако се познати вредностите: ; ; ; ; ; ; ; .

Решение.

По прекрстување на нултите коефициенти добиваме:

=1;

=1;

=1.

Да го изедначиме со еден коефициентот што одговара на сврзникот на најнискиот ранг и претворајќи ги последните четири равенки на 1, а во првата равенка препорачливо е да се изедначи коефициентот со 1. Останатите коефициенти се поставени на 0.

Одговори: тип на минимизирана функција.

Треба да се напомене дека методот на неопределени коефициенти е ефективен кога бројот на променливи е мал и не надминува 5-6.

Повеќедимензионална коцка

Да разгледаме графички приказ на функција во форма на повеќедимензионална коцка. Секој врв n-димензионална коцка може да се стави во кореспонденција со конституентот на единицата.

Подмножеството означени темиња е пресликување на n-димензионална коцка на Булова функција од nпроменливи во SDNF.

За прикажување на функцијата од nпроменливи претставени во кој било DNF, неопходно е да се воспостави кореспонденција помеѓу неговите минитерми и елементи n-димензионална коцка.

Минитерми од (n-1) ранг може да се смета како резултат на лепење заедно два минитерми n-ти ранг, т.е.

На n-димензионална коцка што одговара на замена на две темиња кои се разликуваат само во координатни вредности x i, поврзувајќи ги овие темиња со раб (се вели дека раб ги покрива темињата што се спаѓаат со него).

Така, минитерми ( nРедот -1) одговара на рабовите на n-димензионална коцка.

Слично на тоа, кореспонденцијата на минитерми ( n-2)ти ред лица n-димензионална коцка, од која секоја покрива четири темиња (и четири рабови).

Елементи n-димензионална коцка, се карактеризира со Смерењата се нарекуваат С- коцки

Значи темињата се 0-коцки, рабовите се 1-коцки, лицата се 2-коцки итн.

Сумирајќи, можеме да кажеме дека минитермот ( n-S) рангирање во DNF за функцијата nприкажани променливи С-коцка, секоја С-коцка ги опфаќа сите оние коцки со пониска димензија кои се поврзани само со нејзините темиња.

Пример. На сл. со оглед на мапирањето

Тука минитерми и одговараат на 1-коцки ( С=3-2=1), и минитерум x 3прикажан на 2-коцки ( С=3-1=2).

Значи, секој DNF е мапиран n-димензионална коцка во целост С-коцки кои ги покриваат сите темиња што одговараат на составните единици (0-коцка).

Конституенти. За променливи x 1,x 2,…x nизразување се нарекува составен дел на единицата, и - составен дел од нула (значи или или).

Оваа состојка од една (нула) се претвора во една (нула) само со едно соодветно множество на вредности на променливи, кое се добива ако сите променливи се земат еднакви на една (нула), а нивните негации еднакви на нула (еден).

На пример: конститутивната одговара на множеството (1011), а составната нула - сет (1001).

Бидејќи SD(K)NF е дисјункција (сврзник) на составните делови на еден (нула), може да се тврди дека Буловата функција што ја претставува ѓ(x 1, x 2,…, x n) се претвора во една (нула) само за множества на променливи вредности x 1, x 2,…, x n, што одговара на овие коститути. Во други сетови оваа функција се претвора во 0 (еден).

Вистина е и спротивната изјава, на која се заснова начин на претставување на која билоБулова функција наведена во табелата.

За да го направите ова, неопходно е да се напишат дисјункции (сврзници) на конституентите на еден (нула), што одговара на множества вредности на променливи на кои функцијата зема вредност еднаква на една (нула).

На пример, функција дадена од табела

одговараат

Добиените изрази може да се претворат во друга форма заснована на својствата на алгебрата на логиката.

Вистина е и обратната изјава: ако некоја збирка С-коцките го опфаќаат множеството од сите темиња што одговараат на единечните вредности на функцијата, потоа дисјункцијата што одговара на овие С-коцки од минитерми е изразот на оваа функција во DNF.

Велат дека таква колекција С-коцки (или нивните соодветни минитерми) формираат покривка на функцијата. Желбата за минимална форма интуитивно се сфаќа како потрага по таква покривка, бројка С-од кои би имало помалку коцки, и нивните димензии С- повеќе. Покриеноста што одговара на минималната форма се нарекува минимална покриеност.

На пример, за функцијата на= облогата одговара на неминимална форма.

Еднаквоста (I) е идентитет. Сведувајќи го во цел број, добиваме еднаквост на 2 полиноми. Но, таквата еднаквост секогаш се задоволува само под услов на еднаквост поим по член на овие полиноми.

Изедначувајќи ги коефициентите за исти сили на x на левата и десната страна на еднаквоста, добиваме систем на линеарни равенки за непознати коефициенти кои мора да се решат.

Бидејќи експанзијата (I) секогаш постои за која било соодветна рационална дропка, добиениот систем е секогаш конзистентен.

Овој метод на наоѓање коефициенти се нарекува метод на неизвесни коефициенти (метод на споредување коефициенти).

Да дадеме пример за разложување на рационална функција на елементарни дропки.

Пример 6.6.27. Разложете ги дропките на елементарни дропки.

заменете ја последната равенка со втората

Така,
.

x=2 ;

x=3 .

Треба да; .

Методот на делумна вредност бара помалку труд и затоа заслужува посебно внимание при интегрирање на рационални фракции.

Ако корените на именителот се само реални, тогаш препорачливо е да се користи овој метод за да се одредат непознати коефициенти.

Во други случаи, двата методи може да се комбинираат за да се утврдат непознати коефициенти.

Коментар. Методот на парцијални вредности се користи и во други случаи, но тука идентитетот мора да се разликува.

Така, за да се интегрираат правилни рационални дропки, доволно е да се биде во можност:

1) интегрира елементарни дропки;

2) разложува рационални дропки на елементарни.

3. Интеграција на рационални дропки

Шема за интегрирање на рационални дропки:

Да се ​​интегрираат рационални дропки ;

Онаму каде што P(x) и Q(x) се полиноми со реални коефициенти, три чекори се изведуваат последователно.

Првиот чекор. Ако дропката е неправилна, односно степенот на броителот P(x) е поголем или еднаков на степенот на именителот Q(x), изолирајте го целиот дел од рационалната дропка со делење на броителот со именителот според на правилото за делење на полином со полином. По ова, рационалната дропка може да се напише како збир:

1) избраниот цел број – полиномот M(x);

2) правилна преостаната дропка :

Втор чекор.

Правилна преостаната дропка распаднат на следните фракции.

За да го направите ова, пронајдете ги корените на равенката Q(x)=0 и разложете го именителот Q(x) на фактори од првиот и вториот степен со реални коефициенти:

Во ова проширување на именителот, факторите од 1 степен одговараат на вистински корени, а факторите од 2 степен одговараат на паралелни конјугирани корени.

Коефициентот за поголем степен на x во именителот Q(x) може да се смета за еднаков на 1, бидејќи тоа секогаш може да се постигне со делење на P(x) и Q(x) со него.

По ова, соодветната преостаната дропка се разложува на наједноставни (елементарни) фракции.

Трет чекор. Најдете ги интегралите на избраниот целоброен дел и сите елементарни дропки (со користење на методите опишани погоре), кои потоа се додаваат.

Пример6.6.28.

Под интегралниот знак има неправилна рационална дропка, бидејќи степенот на броителот е еднаков на степенот на именителот, затоа го избираме целобројниот дел.

МИНИСТЕРСТВО ЗА НАУКА И ОБРАЗОВАНИЕ НА РЕПУБЛИКА БАШКОРТО СТАН

САОУ СПО Башкирски колеџ за архитектура и градежништво

Калиулин Асхат Аделзјанович,

наставник по математика на Башкирски

Колеџ за архитектура и градежништво

УФА

2014 година

Вовед _________________________________________________3

Поглавје Јас. Теоретски аспекти на користење на методот на неизвесни коефициенти________________________________________________4

Поглавје II. Бара решенија за проблеми со полиноми со методот на неопределени коефициенти________________________________7

2.1.Факторирање на полином___________________ 7

2.2. Проблеми со параметри________________________________ 10

2.3. Решавање равенки________________________________________________14

2.4. Функционални равенки________________________________19

Заклучок________________________________________________23

Список на користена литература________________________________________________24

Апликација ________________________________________________25

Вовед.

Овој труд е посветен на теоретските и практичните аспекти на воведувањето на методот на неопределени коефициенти во училишниот курс по математика. Релевантноста на оваа тема е одредена од следните околности.

Никој нема да тврди дека математиката како наука не стои на едно место, таа постојано се развива, се појавуваат нови задачи со зголемена сложеност, што често предизвикува одредени тешкотии, бидејќи овие задачи обично се поврзуваат со истражување. Во последниве години, вакви проблеми се предлагаат на училишните, областите и републичките математички олимпијади, а достапни се и во верзиите за обединет државен испит. Затоа, беше потребен посебен метод кој ќе овозможи барем некои од нив да се решат најбрзо, ефикасно и најприфатливо. Ова дело јасно ја прикажува содржината на методот на неопределени коефициенти, кој е широко користен во широк спектар на области од математиката, почнувајќи од прашања вклучени во курсот за општо образование до неговите најнапредни делови. Посебно, особено интересни и ефективни се примената на методот на неопределени коефициенти при решавање проблеми со параметри, фракциони рационални и функционални равенки; лесно можат да ги заинтересираат сите заинтересирани за математика. Главната цел на предложената работа и изборот на проблеми е да се обезбедат големи можности за усовршување и развивање на способноста за изнаоѓање кратки и нестандардни решенија.

Ова дело се состои од две поглавја. Првиот ги разгледува теоретските аспекти на користењето

метод на неизвесни коефициенти, и второ, практични и методолошки аспекти на таквата употреба.

Додатокот на трудот дава услови за конкретни задачи за самостојно решавање.

Поглавје Јас . Теоретски аспекти на употребаметод на неизвесни коефициенти

„Човекот... е роден да биде мајстор,

владетел, крал на природата, но мудрост,

со која мора да владее не му се дава

од раѓање: се стекнува со учење“

Н.И.Лобачевски

Постојат различни начини и методи за решавање проблеми, но еден од најзгодните, најефикасните, оригиналните, елегантни и во исто време многу едноставни и разбирливи за секого е методот на неопределени коефициенти. Методот на неодредени коефициенти е метод кој се користи во математиката за да се најдат коефициентите на изразите чија форма е однапред позната.

Пред да ја разгледаме примената на методот на неопределени коефициенти за решавање на разни видови проблеми, презентираме голем број теоретски информации.

Нека се дадат

А n (x) = а 0 x n + а 1 x n-1 + а 2 x n-2 + ··· + а n-1 x + а n

Б м (x ) = б 0 x м + б 1 x м -1 + б 2 x м -2 + ··· + б m-1 x + б м ,

полиноми релативни Xсо какви било шанси.

Теорема. Два полиноми во зависност од еден и истите аргументи се идентично еднакви ако и само акоn = м а нивните соодветни коефициенти се еднаквиа 0 = б 0 , а 1 = б 1 , а 2 = б 2 ,··· , а n -1 = б м -1 , а n = б м И Т. г.

Очигледно, еднаквите полиноми ги земаат сите вредности Xисти вредности. Спротивно на тоа, ако вредностите на два полиноми се еднакви за сите вредности X, потоа полиномите се еднакви, односно нивните коефициенти на исти степениXпоклопуваат.

Затоа, идејата за примена на методот на неопределени коефициенти за решавање на проблемите е како што следува.

Да знаеме дека како резултат на некои трансформации се добива израз од одреден тип и само коефициентите во овој израз се непознати. Тогаш овие коефициенти се означени со букви и се сметаат за непознати. Потоа се конструира систем од равенки за да се одредат овие непознати.

На пример, во случај на полиноми, овие равенки се направени од условот коефициентите да се еднакви за истите моќи Xза два еднакви полиноми.

Ќе го прикажеме она што беше кажано погоре користејќи ги следните конкретни примери и да започнеме со наједноставниот.

Така, на пример, врз основа на теоретски размислувања, дропот

може да се претстави како збир

, Каде а , б И в - коефициентите што треба да се утврдат. За да ги најдеме, го изедначуваме вториот израз со првиот:

=

и ослободување од именителот и собирање термини со исти овластувања лево X, добиваме:

(а + б + в )X 2 + ( б - в )x - a = 2X 2 – 5 X– 1

Бидејќи последната еднаквост мора да важи за сите вредности X, потоа коефициентите на исти моќиXдесно и лево треба да бидат исти. Така, се добиваат три равенки за одредување на трите непознати коефициенти:

а+б+в = 2

б - в = - 5

А= 1, од каде а = 1 , б = - 2 , в = 3

Оттука,

=
,

валидноста на оваа еднаквост е лесно да се потврди директно.

Да претпоставиме дека треба да претставувате и дропка

како а + б
+ в
+ г
, Каде а , б , в И г- непознати рационални коефициенти. Вториот израз го поистоветуваме со првиот:

а + б
+ в
+ г
=
или, Ослободувајќи се од именителот, отстранувајќи, каде што е можно, рационалните фактори од под знаците на корените и внесувајќи слични термини на левата страна, добиваме:

(а- 2 б + 3 в ) + (- а+б +3 г )
+ (a+c - 2 г )
+

+ (б - в + г )
= 1 +
-
.

Но, таквата еднаквост е можна само во случај кога рационалните членови на двата дела и коефициентите на истите радикали се еднакви. Така се добиваат четири равенки за пронаоѓање на непознатите коефициенти а , б , в И г :

а- 2b+ 3в = 1

- а+б +3 г = 1

a+c - 2 г = - 1

б - в + г= 0, од ​​каде а = 0 ; б = - ; в = 0 ; г= т.е
= -
+
.

Поглавје II. Бара решенија за проблеми со полиноми метод на неодредени коефициенти.

„Ништо не придонесува за совладување на предметот подобро од

начин да се постапува со него во различни ситуации“

Академик Б.В.Гнеденко

2. 1. Факторирање на полином.

Методи за факторинг на полиноми:

1) ставање на заедничкиот фактор надвор од загради 2) метод на групирање; 3) примена на основните формули за множење; 4) воведување на помошни поими 5) прелиминарна трансформација на даден полином со употреба на одредени формули; 6) проширување со наоѓање на корените на даден полином; 7) начин на внесување на параметарот; 8)метод на неодредени коефициенти.

Задача 1. Факторирајте го полиномот во реални множители X 4 + X 2 + 1 .

Решение. Нема корени меѓу делителите на слободниот член на овој полином. Не можеме да ги најдеме корените на полиномот со други елементарни средства. Според тоа, не е можно да се изврши потребното проширување со прво наоѓање на корените на овој полином. Останува да се бара решение за проблемот или со воведување на помошни поими или со методот на неодредени коефициенти. Очигледно е дека X 4 + X 2 + 1 = X 4 + X 3 + X 2 - X 3 - X 2 - X + X 2 + X + 1 =

= X 2 (X 2 + X + 1) - X (X 2 + X + 1) + X 2 + X + 1 =

= (X 2 + X + 1)(X 2 - X + 1).

Добиените квадратни триноми немаат корени и затоа се неразградливи на реални линеарни фактори.

Опишаниот метод е технички едноставен, но тежок поради неговата извештаченост. Навистина, многу е тешко да се дојде до потребните помошни термини. Само претпоставка ни помогна да го најдеме ова распаѓање. Но

Постојат посигурни начини за решавање на ваквите проблеми.

Може да се продолжи вака: да се претпостави дека дадениот полином се распаѓа во производот

(X 2 + А X + б )(X 2 + в X + г )

два квадратни триноми со целобројни коефициенти.

Така ќе го имаме тоа

X 4 + X 2 + 1 = (X 2 + А X + б )(X 2 + в X + г )

Останува да се утврдат коефициентитеа , б , в И г .

Со множење на полиномите од десната страна на последното равенство, добиваме:X 4 + X 2 + 1 = X 4 +

+ (a + c ) X 3 + (б + А в + г ) X 2 + (реклама + п.н.е ) x + bd .

Но, бидејќи ни треба десната страна на оваа еднаквост да се претвори во истиот полином што е на левата страна, ќе бараме да се исполнат следниве услови:

a + c = 0

б + А в + г = 1

реклама + п.н.е = 0

bd = 1 .

Резултатот е систем од четири равенки со четири непознатиа , б , в И г . Лесно е да се најдат коефициентите од овој система = 1 , б = 1 , в = -1 И г = 1.

Сега проблемот е целосно решен. Добивме:

X 4 + X 2 + 1 = (X 2 + X + 1)(X 2 - X + 1).

Задача 2. Факторирајте го полиномот во реални множители X 3 – 6 X 2 + 14 X – 15 .

Решение. Да го претставиме овој полином во форма

X 3 – 6 X 2 + 14 X – 15 = (X + А )(X 2 + bx + в), Каде а , б И Со - коефициенти се уште не се утврдени. Бидејќи два полиноми се идентично еднакви ако и само ако коефициентите на исти силиX се еднакви, тогаш, изедначувајќи ги коефициентите соодветно заX 2 , X и слободни членови, добиваме систем од три равенки со три непознати:

а+б= - 6

ab + c = 14

ак = - 15 .

Решението на овој систем ќе биде значително поедноставено ако се земе предвид дека бројот 3 (делител на слободниот член) е коренот на оваа равенка, и затоа,а = - 3 ,

б = - 3 И Со = 5 .

Потоа X 3 – 6 X 2 + 14 X – 15 = (X – 3)(X 2 – 3 x + 5).

Применетиот метод на неопределени коефициенти, во споредба со горенаведениот метод на воведување на помошни поими, не содржи ништо вештачко, но бара примена на многу теоретски принципи и е придружен со прилично големи пресметки. За полиноми со повисок степен, овој метод на неодредени коефициенти води до гломазни системи на равенки.

2.2.Задачи и со параметри.

Во последниве години, верзиите на Единствениот државен испит нудат задачи со параметри. Нивното решение често предизвикува одредени тешкотии. Кога решавате проблеми со параметри, заедно со други методи, можете доста ефикасно да го користите методот на неопределени коефициенти. Токму овој метод ви овозможува во голема мера да го поедноставите нивното решение и брзо да добиете одговор.

Задача 3. Определете во кои вредности на параметарот Аравенка 2 X 3 – 3 X 2 – 36 X + А – 3 = 0 има точно два корени.

Решение. 1 начин. Користење на дериват.

Да ја претставиме оваа равенка во форма на две функции

2x3 – 3 X 2 – 36 X – 3 = – А .

ѓ (x) = 2x 3 – 3 X 2 – 36 X– 3 и φ( X ) = – А .

Ајде да ја истражиме функцијатаѓ (x) = 2x 3 – 3 X 2 – 36 X – 3 користејќи го изводот и шематски конструирај го неговиот график (сл. 1.).

f( – x )ѓ (x ) , ѓ (– x ) – ѓ (x ). Функцијата не е ниту парна ниту непарна.

3. Да ги најдеме критичните точки на функцијата, нејзините интервали на зголемување и намалување, екстреми. ѓ / (x ) = 6 x 2 – 6 X – 36. Д (ѓ / ) = Р , затоа ќе ги најдеме сите критични точки на функцијата со решавање на равенката ѓ / (x ) = 0 .

6(X 2 – X– 6) = 0 ,

X 2 – X– 6 = 0 ,

X 1 = 3 , X 2 = – 2 според теоремата инверзна на теоремата на Виета.

ѓ / (x ) = 6(X – 3)(X + 2).

+ макс - мин +

2 3 x

ѓ / (x) > 0 за сите X< – 2 и X > 3 и функцијата е континуирана во точкитеx =– 2 и X = 3, според тоа, се зголемува на секој од интервалите (- ; - 2] и [3; ).

ѓ / (x ) < 0 на - 2 < X< 3, според тоа, се намалува на интервалот [- 2; 3 ].

X = - 2-ри максимален поен, бидејќи во овој момент знакот на изводот се менува од„+“ до „-“.

ѓ (– 2) = 2· (– 8) – 3·4 – 36·(– 2) – 3 = – 16 – 12 + 72 – 3 == 72 – 31 = 41 ,

x = 3 минимум поени, бидејќи во овој момент се менува знакот на дериватот„-“ до „+“.

ѓ (3) = 2·27 – 3·9 – 36·3 – 3 = 54 – 27 – 108 – 3 = – 138 + +54 = – 84.

График на функцијата φ(X ) = – А е права линија паралелна на оската x и минува низ точката со координати (0; – А ). Графиконите имаат две заеднички точки на -А= 41, т.е. a =– 41 и – А= – 84, т.е. А = 84 .

на

41φ( X)

2 3 X

3 ѓ ( x ) = 2x3 – 3 X 2 – 36 X – 3

Метод 2. Метод на неодредени коефициенти.

Бидејќи, според условите на проблемот, оваа равенка мора да има само два корени, еднаквоста е очигледна:

2X 3 – 3 X 2 – 36 X + А – 3 = (x + б ) 2 (2 x + в ) ,

2X 3 – 3 X 2 – 36 X + А – 3 = 2 x 3 + (4 б + в ) x 2 + (2 б 2 + +2 п.н.е ) x + б 2 в ,

Сега изедначувајќи ги коефициентите на истите степени X, добиваме систем од равенки

4 b + c = - 3

2б 2 + 2п.н.е. = - 36

б 2 в = а – 3 .

Од првите две равенки на системот наоѓамеб 2 + б – 6 = 0, од ​​каде б 1 = - 3 или б 2 = 2. Соодветни вредностиСо 1 и Со 2 лесно да се најде од првата равенка на системот:Со 1 = 9 или Со 2 = - 11 . Конечно, саканата вредност на параметарот може да се одреди од последната равенка на системот:

А = б 2 в + 3 , а 1 = - 41 или а 2 = 84.

Одговор: оваа равенка има точно две различни

корен во А= - 41 и А= 84 .

Задача 4. Најдете ја најголемата вредност на параметаротА , за што равенкатаX 3 + 5 X 2 + О + б = 0

со целобројни коефициенти има три различни корени, од кои едниот е еднаков на – 2.

Решение. 1 начин. Замена X= - 2 на левата страна на равенката, добиваме

8 + 20 – 2 А + б= 0, што значи б = 2 а – 12 .

Бидејќи бројот - 2 е корен, можеме да го извадиме заедничкиот фактор X + 2:

X 3 + 5 X 2 + О + б = X 3 + 2 X 2 + 3 X 2 + О + (2 а – 12) =

= x 2 (X + 2) + 3 x (X + 2) – 6 x + О + (2 а – 12) =

= x 2 (X + 2) + 3 x (X + 2) + (а – 6)(x +2) - 2(а – 6)+ (2 а - 12) =

= (X + 2)(X 2 + 3 x + (а – 6) ) .

По услов, има уште два корени на равенката. Тоа значи дека дискриминаторот на вториот фактор е позитивен.

Д =3 2 - 4 (а – 6) = 33 – 4 а > 0, т.е А < 8,25 .

Се чини дека одговорот ќе биде a = 8 . Но, кога ќе го замениме бројот 8 во првобитната равенка, добиваме:

X 3 + 5 X 2 + О + б = X 3 + 5 X 2 + 8 X + 4 = (X + 2)(X 2 + 3 x + 2 ) =

= (X + 1) (X + 2) 2 ,

односно равенката има само два различни корени. Но кога a = 7 всушност произведува три различни корени.

Метод 2. Метод на неодредени коефициенти.

Ако равенката X 3 + 5 X 2 + О + б = 0 има корен X = - 2, тогаш секогаш можете да ги соберете броевитев И г така што пред ситеX еднаквоста беше вистина

X 3 + 5 X 2 + О + б = (X + 2)(X 2 + Со x + г ).

За да најдете броевив И г Ајде да ги отвориме заградите од десната страна, да додадеме слични термини и да добиеме

X 3 + 5 X 2 + О + б = X 3 + (2 + Со ) X 2 +(2 s + г ) X + 2 г

Изедначување на коефициентите на соодветните моќи Xимаме систем

2 + Со = 5

2 Со + г = а

2 г = б , каде c = 3 .

Оттука, X 2 + 3 x + г = 0 , Д = 9 – 4 г > 0 или

г < 2.25, значи г (- ; 2 ].

Проблемските услови се задоволуваат со вредноста г = 1 . Конечната сакана вредност на параметаротА = 7.

ОДГОВОР: кога a = 7 оваа равенка има три различни корени.

2.3. Решавање равенки.

„Запомнете дека решавате мали проблеми

подгответе се да се справите со големи и тешки

нови задачи“.

Академик С.Л.Соболев

Кога решавате некои равенки, можете и треба да покажете снаодливост и духовитост и да користите специјални техники. Совладувањето на различни техники на трансформација и способноста за спроведување на логично расудување е од големо значење во математиката. Еден од овие трикови е да додадете и одземете некој добро избран израз или број. Самиот наведен факт, се разбира, е добро познат на сите - главната тешкотија е да се видат во специфична конфигурација оние трансформации на равенки на кои е погодно и целисходно да се примени.

Користејќи едноставна алгебарска равенка, ќе илустрираме една нестандардна техника за решавање равенки.

Задача 5. Решете ја равенката

=
.

Решение. Ајде да ги помножиме двете страни на оваа равенка со 5 и да ја преработиме на следниов начин

= 0 ; X 0; -
;

= 0 ,

= 0 ,

= 0 или
= 0

Дозволете ни да ги решиме добиените равенки користејќи го методот на неодредени коефициенти

X 4 - X 3 –7 X – 3 = (X 2 + ах + б )(x 2 + cx + г ) = 0

X 4 - X 3 –7 X – 3 = X 4 + (a + c ) X 3 + (б + А в + г ) X 2 + (реклама + п.н.е ) x+ + bd

Изедначување на коефициентите во X 3 , X 2 , Xи бесплатни услови, го добиваме системот

a + c = -1

б + А в + г = 0

реклама + п.н.е = -7

bd = -3, од каде наоѓаме:А = -2 ; б = - 1 ;

Со = 1 ; г = 3 .

Значи X 4 - X 3 –7X– 3 = (X 2 – 2 X – 1)(X 2 + X + 3) = 0 ,

X 2 – 2 X– 1 = 0 или X 2 + X + 3 = 0

X 1,2 =
без корени.

Слично и ние имаме

X 4 – 12X – 5 = (X 2 – 2 X – 1)(X 2 + 2X + 5) = 0 ,

каде X 2 + 2 X + 5 = 0 , Д = - 16 < 0 , нет корней.

Одговор: X 1,2 =

Задача 6. Решете ја равенката

= 10.

Решение. За да ја решите оваа равенка треба да изберете броевиАИ б така што броителите на двете дропки се исти. Затоа, го имаме системот:

= 0 , X 0; -1 ; -

= - 10

Значи, задачата е да се најдат броевитеАИ б , за кои важи еднаквоста

(a + 6) X 2 + ах - 5 = X 2 + (5 + 2 б ) x + б

Сега, според теоремата за еднаквоста на полиномите, неопходно е десната страна на оваа еднаквост да се претвори во истиот полином што е на левата страна.

Со други зборови, односите мора да бидат задоволни

a + 6 = 1

А = 5 + 2 б

– 5 = б , од каде ги наоѓаме вредноститеА = - 5 ;

б = - 5 .

На овие вредностиАИ б еднаквост А + б = - 10 е исто така фер.

= 0 , X 0; -1 ; -

= 0 ,

= 0 ,

(X 2 – 5X– 5)(X 2 + 3X + 1) = 0 ,

X 2 – 5X– 5 = 0 или X 2 + 3X + 1 = 0 ,

X 1,2 =
, X 3,4 =

Одговор: X 1,2 =
, X 3,4 =

Задача 7. Решете ја равенката

= 4

Решение. Оваа равенка е посложена од претходните и затоа ќе ја групираме вака: X 0;-1;3;-8;12

0 ,

= - 4.

Од условот за еднаквост на два полиноми

О 2 + (a + 6) X + 12 = X 2 + (б + 11) x – 3 б ,

добиваме и решаваме систем од равенки за непознати коефициентиАИ б :

А = 1

a + 6 = б + 11

12 = – 3 б , каде a = 1 , б = - 4 .

Полиноми - 3 – 6X + cx 2 + 8 cxИ X 2 + 21 + 12 г – dx се еднакви едни на други идентично само кога

Со = 1

8 со - 6 = - г

3 = 21 + 12 г , Со = 1 , г = - 2 .

Со вредностиa = 1 , б = - 4 , Со = 1 , г = - 2

еднаквост
= - 4 е точно.

Како резултат на тоа, оваа равенка ја добива следната форма:

= 0 или
= 0 или
= 0 ,

= - 4 , = - 3 , = 1 , = -
.

Од разгледаните примери, јасно е како вешто користењето на методот на неопределени коефициенти,

помага да се поедностави решението на прилично сложена, необична равенка.

2.4. Функционални равенки.

„Највисоката цел на математиката... е

е да се најде скриениот редослед во

хаос што не опкружува“

Н. Винер

Функционалните равенки се многу општа класа на равенки во кои непознатата функција е одредена функција. Функционална равенка во потесна смисла на зборот се подразбира како равенки во кои саканите функции се поврзани со познати функции на една или повеќе променливи користејќи ја операцијата за формирање сложена функција. Функционална равенка може да се смета и како израз на својство што карактеризира одредена класа на функции

[на пример, функционална равенка ѓ ( x ) = ѓ (- x ) ја карактеризира класата парни функции, функционалната равенкаѓ (x + 1) = ѓ (x ) – класа на функции со период 1 итн.].

Една од наједноставните функционални равенки е равенкатаѓ (x + y ) = ѓ (x ) + ѓ (y ). Континуираните решенија на оваа функционална равенка имаат форма

ѓ (x ) = Вx . Меѓутоа, во класата на дисконтинуирани функции оваа функционална равенка има и други решенија. Поврзани со разгледуваната функционална равенка се

ѓ (x + y ) = ѓ (x ) · ѓ (y ), ѓ (x y ) = ѓ (x ) + ѓ (y ), ѓ (x y ) = ѓ (x )· ѓ (y ),

континуирани решенија, кои, соодветно, имаат форма

д cx , СОlnx , x α (x > 0).

Така, овие функционални равенки може да се користат за дефинирање на експоненцијални, логаритамски и моќни функции.

Најраспространети се равенките во сложените функции во кои бараните функции се надворешни функции. Теоретски и практични примени

Токму овие равенки ги поттикнаа извонредните математичари да ги проучуваат.

На пример, наусогласување

ѓ 2 (x) = ѓ (x - y)· ѓ (x + y)

Н.И.Лобачевскисе користи при определување на аголот на паралелизам во мојата геометрија.

Во последниве години, проблемите поврзани со решавање на функционални равенки доста често се нудат на математичките олимпијади. За нивното решение не е потребно знаење надвор од опсегот на наставната програма по математика во средните училишта. Меѓутоа, решавањето функционални равенки често предизвикува одредени тешкотии.

Еден од начините за наоѓање решенија на функционални равенки е методот на неопределени коефициенти. Може да се користи кога општата форма на саканата функција може да се одреди со изгледот на равенката. Ова се однесува, пред сè, за оние случаи кога решенијата на равенките треба да се бараат меѓу целобројни или фракциони рационални функции.

Дозволете ни да ја претставиме суштината на оваа техника со решавање на следните проблеми.

Задача 8. Функцијаѓ (x ) е дефинирана за сите реални x и задоволува за ситеX Р состојба

3 ѓ(x) - 2 ѓ(1- x) = x 2 .

Најдетеѓ (x ).

Решение. Бидејќи на левата страна на оваа равенка над независната променлива x и вредностите на функцијатаѓ Се вршат само линеарни операции, а десната страна на равенката е квадратна функција, тогаш природно е да се претпостави дека саканата функција е исто така квадратна:

ѓ (X) = секира 2 + bx + в , Кадеа, б, в – коефициенти да се утврдат, односно неизвесни коефициенти.

Заменувајќи ја функцијата во равенката, доаѓаме до идентитетот:

3(секира 2 + bx+ в) – 2(а(1 – x) 2 + б(1 – x) + в) = x 2 .

секира 2 + (5 б + 4 а) x + (в – 2 а – 2 б) = x 2 .

Два полиноми ќе бидат идентично еднакви ако се еднакви

коефициенти за истите моќи на променливата:

а = 1

5б + 4а = 0

в– 2 а – 2 б = 0.

Од овој систем ги наоѓаме коефициентите

а = 1 , б = - , в = , Исто таказадоволуваеднаквост

3 ѓ (x ) - 2 ѓ (1- x ) = x 2 на множеството на сите реални броеви. Во исто време, постои таковx 0 Задача 9. Функцијаy =ѓ(x) за сите x е дефинирано, континуирано и го задоволува условотѓ (ѓ (x)) – ѓ(x) = 1 + 2 x . Најдете две такви функции.

Решение. На саканата функција се вршат две дејства - операција на составување сложена функција и

одземање. Имајќи предвид дека десната страна на равенката е линеарна функција, природно е да се претпостави дека саканата функција е исто така линеарна:ѓ(x) = ах +б , КадеА Иб – неизвесни коефициенти. Заменувајќи ја оваа функција воѓ (ѓ ( (x ) = - X - 1 ;

ѓ 2 (x ) = 2 X+ , кои се решенија на функционалната равенкаѓ (ѓ (x)) – ѓ(x) = 1 + 2 x .

Заклучок.

Како заклучок, треба да се истакне дека оваа работа секако ќе придонесе за понатамошно проучување на оригинален и ефективен метод за решавање на различни математички проблеми, кои се проблеми со зголемена тежина и бараат длабоко познавање на училишниот курс по математика и високо логично култура.Секој кој сака самостојно да ги продлабочи своите знаења од математиката ќе најде и Ова дело содржи материјал за размислување и интересни задачи чиешто решение ќе донесе корист и задоволство.

Работата, во рамките на постојната училишна програма и во форма достапна за ефективна перцепција, го поставува методот на неопределени коефициенти, што помага да се продлабочи училишниот курс по математика.

Се разбира, сите можности на методот на неопределени коефициенти не можат да се покажат во една работа. Всушност, методот сè уште бара дополнително проучување и истражување.

Список на користена литература.

Глејзер Г.И..Историја на математиката во училиште.-М.: Образование, 1983 година.

Гомонов С.А. Функционални равенки во училишен курс по математика // Математика на училиште. – 2000 година. -№10 .

Дорофеев Г.В., Потапов М.К., Розов Н.Х.. Прирачник за математика - М.: Наука, 1972 година.

Курош А.Г. Алгебарски равенки на произволни степени - М.: Наука, 1983 година.

Лихтарников Л.М.. Елементарен вовед во функционални равенки. – Санкт Петербург. : Лан, 1997 година.

Мантуров О.В., Солнцев Ју.К., Сорокин Ју.И., Федин Н.Г.. Објаснувачки речник на математички поими.-М.: Образование, 1971 г.

Modenov V.P.. Прирачник по математика. Дел 1.-М.: Московски државен универзитет, 1977 година.

Моденов В.П.. Проблеми со параметри - М.: Испит, 2006 година.

Потапов М.К., Александров В.В., Пасиченко П.И.. Алгебра и анализа на елементарните функции - М.: Наука, 1980 г.

Khaliullin A.A.. Можете полесно да го решите // Математика на училиште. – 2003 . - №8 .

Калиулин.

4. Рашири го полиномот 2X 4 – 5X 3 + 9X 2 – 5X+ 3 за множители со целобројни коефициенти.

5. По која вредност А X 3 + 6X 2 + О+ 12 по X+ 4 ?

6. Со која вредност на параметаротА равенкатаX 3 +5 X 2 + + О + б = 0 со целобројни коефициенти има два различни корени, од кои едниот е 1 ?

7. Меѓу корените на полиномот X 4 + X 3 – 18X 2 + О + б со целобројни коефициенти има три еднакви цели броеви. Најдете ја вредноста б .

8. Најдете ја најголемата цел бројна вредност на параметарот А,при што равенката X 3 – 8X 2 + ах +б = 0 со целобројни коефициенти има три различни корени, од кои едниот е еднаков на 2.

9. По кои вредности АИ б делењето се врши без остаток X 4 + 3X 3 – 2X 2 + О + б на X 2 – 3X + 2 ?

10. Факторски полиноми:

А)X 4 + 2 X 2 – X + 2 V)X 4 – 4X 3 +9X 2 –8X + 5 г)X 4 + 12X – 5

б)X 4 + 3X 2 + 2X + 3 G)X 4 – 3X –2 д)X 4 – 7X 2 + 1 .

11. Решете ги равенките:

А)
= 2 = 2 ѓ (1 – X ) = X 2 .

Најдете ѓ (X) .

13. Функција на= ѓ (X) пред сите Xдефинирана, континуирана и ја задоволува состојбата ѓ ( ѓ (X)) = ѓ (X) + X.Најдете две такви функции.

Интеграција на фракционо-рационална функција.
Метод на неизвесен коефициент

Продолжуваме да работиме на интегрирање на дропки. Веќе разгледавме интеграли на некои типови дропки во лекцијата, а оваа лекција, во извесна смисла, може да се смета за продолжение. За успешно разбирање на материјалот, потребни се основни вештини за интеграција, па ако штотуку сте почнале да ги проучувате интегралите, односно сте почетник, тогаш треба да започнете со статијата Неопределен интеграл. Примери на решенија.

Доволно чудно, сега ќе се занимаваме не толку со наоѓање интеграли, туку... со решавање системи на линеарни равенки. Во таа смисла УргентноПрепорачувам да ја посетувате лекцијата, имено, треба добро да ги познавате методите за замена (методот „училиште“ и методот на собирање (одземање) на системски равенки по член).

Што е фракциона рационална функција? Со едноставни зборови, дробно-рационална функција е дропка чиј броител и именител содржат полиноми или производи од полиноми. Покрај тоа, фракциите се пософистицирани од оние што се дискутирани во статијата Интегрирање на некои дропки.

Интегрирање на правилна фракционо-рационална функција

Веднаш пример и типичен алгоритам за решавање на интеграл на фракционо-рационална функција.

Пример 1

Чекор 1.Првото нешто што СЕКОГАШ го правиме кога решаваме интеграл на фракциона рационална функција е да го разјасниме следново прашање: дали дропката е соодветна?Овој чекор се изведува вербално, а сега ќе објаснам како:

Прво го гледаме броителот и дознаваме виша дипломаполином:

Водечката моќ на броителот е два.

Сега го гледаме именителот и дознаваме виша дипломаименител. Очигледниот начин е да ги отворите заградите и да внесете слични термини, но можете да го направите поедноставно, внатре секојнајдете највисок степен во загради

и ментално множете се: - така, највисокиот степен на именителот е еднаков на три. Сосема е очигледно дека ако навистина ги отвориме заградите, нема да добиеме диплома поголема од три.

Заклучок: Главниот степен на броител СТРОГОе помала од највисоката моќност на именителот, што значи дека дропката е соодветна.

Ако во овој пример броителот го содржи полиномот 3, 4, 5 итн. степени, тогаш дропот би бил погрешно.

Сега ќе ги разгледаме само точните фракциони рационални функции. Случајот кога степенот на броителот е поголем или еднаков на степенот на именителот ќе се дискутира на крајот од часот.

Чекор 2.Да го факторизираме именителот. Да го погледнеме нашиот именител:

Општо земено, ова е веќе производ на фактори, но, сепак, се прашуваме: дали е можно да се прошири нешто друго? Предмет на тортура несомнено ќе биде квадратниот трином. Решавање на квадратната равенка:

Дискриминантата е поголема од нула, што значи дека триномот навистина може да се факторизира:

Општо правило: СЕ во именителот МОЖЕ да се факторизира - факторинг

Ајде да започнеме да формулираме решение:

Чекор 3.Користејќи го методот на неопределени коефициенти, го прошируваме интегранот во збир на едноставни (елементарни) дропки. Сега ќе биде појасно.

Ајде да ја погледнеме нашата интегративна функција:

И, знаете, некако се појавува интуитивна мисла дека би било убаво да ја претвориме нашата голема фракција во неколку мали. На пример, вака:

Се поставува прашањето, дали е воопшто можно да се направи ова? Да здивнеме, соодветната теорема на математичка анализа вели – МОЖНО Е. Таквото распаѓање постои и е единствено.

Има само еден улов, шансите се ЧаоНе знаеме, па оттука и името - методот на неопределени коефициенти.

Како што претпоставувате, последователните движења на телото се такви, не кикнувајте! ќе бидат насочени само кон нивно ПРЕПОЗНАВАЊЕ - да се открие на што се еднакви.

Внимавајте, само еднаш ќе ви објаснам детално!

Значи, да почнеме да танцуваме од:

На левата страна го намалуваме изразот на заеднички именител:

Сега можеме безбедно да се ослободиме од именителот (бидејќи тие се исти):

На левата страна ги отвораме заградите, но засега не ги допирајте непознатите коефициенти:

Во исто време, го повторуваме училишното правило за множење полиноми. Кога бев учител, научив да го изговарам ова правило со директно лице: За да помножите полином со полином, треба да го помножите секој член од еден полином со секој член од другиот полином..

Од гледна точка на јасно објаснување, подобро е да ги ставите коефициентите во загради (иако јас лично никогаш не го правам ова за да заштедам време):

Составуваме систем на линеарни равенки.
Прво бараме високи дипломи:

И ги запишуваме соодветните коефициенти во првата равенка на системот:

Добро запомнете ја следната точка. Што би се случило ако воопшто немало s на десната страна? Да речеме, дали само би се покажал без никаков квадрат? Во овој случај, во равенката на системот би било потребно да се стави нула десно: . Зошто нула? Но затоа што на десната страна секогаш можете да го доделите истиот квадрат со нула: Ако на десната страна нема променливи и/или слободен член, тогаш ставаме нули на десните страни на соодветните равенки на системот.

Ги запишуваме соодветните коефициенти во втората равенка на системот:

И конечно, минерална вода, избираме бесплатни членови.

Ех...некако се шегував. Шегите на страна - математиката е сериозна наука. Во нашата група на институти никој не се смееше кога доцентот рече дека ќе ги расфрли поимите по бројната линија и ќе ги избере најголемите. Ајде да станеме сериозни. Иако... кој ќе доживее да го види крајот на оваа лекција, сепак тивко ќе се насмее.

Системот е подготвен:

Го решаваме системот:

(1) Од првата равенка ја изразуваме и ја заменуваме во 2-та и 3-та равенка на системот. Всушност, беше можно да се изрази (или друга буква) од друга равенка, но во овој случај е поволно да се изрази од првата равенка, бидејќи таму најмалите шанси.

(2) Прикажуваме слични поими во 2-та и 3-та равенка.

(3) Втората и третата равенка ги собираме член по член, добивајќи ја еднаквоста , од која произлегува дека

(4) Заменуваме во втората (или третата) равенка, од каде што го наоѓаме тоа

(5) Заменете и во првата равенка, добивајќи .

Доколку имате потешкотии со методите за решавање на системот, вежбајте ги на час. Како да се реши систем од линеарни равенки?

По решавањето на системот, секогаш е корисно да се провери - заменете ги пронајдените вредности секојравенка на системот, како резултат на тоа, сè треба да се „спојува“.

Скоро таму. Најдени се коефициентите и:

Завршената работа треба да изгледа вака:

Како што можете да видите, главната тешкотија на задачата беше да се состави (точно!) и да се реши (правилно!) систем на линеарни равенки. И во последната фаза, сè не е толку тешко: ги користиме својствата на линеарноста на неопределен интеграл и интегрираме. Забележете дека под секој од трите интеграли имаме „слободна“ комплексна функција; зборував за карактеристиките на нејзината интеграција во лекцијата Метод на промена на променливата во неопределен интеграл.

Проверете: разликувајте го одговорот:

Добиена е оригиналната интегранд функција, што значи дека интегралот е правилно пронајден.
При верификацијата моравме да го сведеме изразот на заеднички именител и тоа не е случајно. Методот на неопределени коефициенти и намалување на изразот на заеднички именител се меѓусебно инверзни дејства.

Пример 2

Најдете го неопределениот интеграл.

Да се ​​вратиме на дропката од првиот пример: . Лесно е да се забележи дека во именителот сите фактори се РАЗЛИЧНИ. Се поставува прашањето, што да се прави ако, на пример, е дадена следнава дропка: ? Овде имаме степени во именителот, или, математички, множители. Дополнително, постои квадратен трином кој не може да се факторизира (лесно е да се потврди дека дискриминантот на равенката е негативен, така што триномот не може да се факторизира). Што да се прави? Проширувањето во збир на елементарни дропки ќе изгледа нешто слично со непознати коефициенти на врвот или нешто друго?

Пример 3

Воведете функција

Чекор 1.Проверка дали имаме правилна дропка
Главен броител: 2
Највисок степен на именител: 8
, што значи дека дропката е точна.

Чекор 2.Дали е можно нешто да се факторизира во именителот? Очигледно не, се е веќе поставено. Квадратниот трином не може да се прошири во производ од причините наведени погоре. Аспиратор. Помалку работа.

Чекор 3.Да замислиме фракционо-рационална функција како збир од елементарни дропки.
Во овој случај, проширувањето ја има следната форма:

Да го погледнеме нашиот именител:
При разложување на фракционо-рационална функција на збир од елементарни дропки, може да се разликуваат три основни точки:

1) Ако именителот содржи фактор „осамен“ до првата моќност (во нашиот случај), тогаш ставаме неодреден коефициент на врвот (во нашиот случај). Примерите бр. 1, 2 се состоеле само од такви „осамени“ фактори.

2) Ако именителот има повеќекратнимножител, тогаш треба да го разложите вака:
- односно, последователно поминете низ сите степени на „Х“ од првиот до n-тиот степен. Во нашиот пример има два повеќекратни фактори: и , погледнете уште еднаш на проширувањето што го дадов и уверете се дека тие се проширени токму според ова правило.

3) Ако именителот содржи неразградлив полином од втор степен (во нашиот случај), тогаш кога се разложувате во броителот треба да напишете линеарна функција со неодредени коефициенти (во нашиот случај со неодредени коефициенти и ).

Впрочем, има уште еден 4-ти случај, но ќе го премолчам, бидејќи во пракса е исклучително редок.

Пример 4

Воведете функција како збир на елементарни дропки со непознати коефициенти.

Ова е пример за да го решите сами. Целосно решение и одговор на крајот од лекцијата.
Строго следете го алгоритмот!

Ако ги разбирате принципите според кои треба да ја проширите фракционо-рационална функција во збир, можете да џвакате речиси секој интеграл од типот што се разгледува.

Пример 5

Најдете го неопределениот интеграл.

Чекор 1.Очигледно дропката е точна:

Чекор 2.Дали е можно нешто да се факторизира во именителот? Може. Еве го збирот на коцки . Факторирајте го именителот со помош на скратената формула за множење

Чекор 3.Користејќи го методот на неопределени коефициенти, го прошируваме интеградот во збир од елементарни дропки:

Забележете дека полиномот не може да се факторизира (проверете дали дискриминантата е негативна), така што најгоре ставаме линеарна функција со непознати коефициенти, а не само една буква.

Дропката ја доведуваме до заеднички именител:

Ајде да го составиме и решиме системот:

(1) Изразуваме од првата равенка и ја заменуваме со втората равенка на системот (ова е најрационален начин).

(2) Прикажуваме слични поими во втората равенка.

(3) Втората и третата равенка на системот ги собираме член по член.

Сите понатамошни пресметки се, во принцип, усни, бидејќи системот е едноставен.

(1) Збирот на дропките го запишуваме во согласност со пронајдените коефициенти.

(2) Ги користиме својствата на линеарноста на неопределен интеграл. Што се случи во вториот интеграл? Можете да се запознаете со овој метод во последниот пасус од лекцијата. Интегрирање на некои дропки.

(3) Уште еднаш ги користиме својствата на линеарноста. Во третиот интеграл започнуваме да го изолираме целосниот квадрат (претпоследниот став од лекцијата Интегрирање на некои дропки).

(4) Го земаме вториот интеграл, во третиот го избираме целосниот квадрат.

(5) Земете го третиот интеграл. Подготвени.