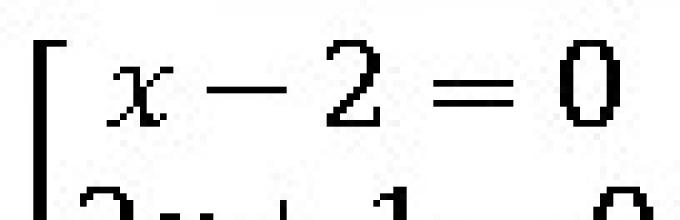Анализа на задача бр.4 на тема: „Решавање равенки од разни видови“
Дополнителни материјали
Почитувани корисници, не заборавајте да ги оставите вашите коментари, критики, желби! Сите материјали се проверени со антивирусна програма.
Едукативни помагала и симулатори во онлајн продавницата Integral за 9 одделение
Интерактивен прирачник „Правила и вежби по алгебра“ за 9 одделение
Мултимедијален учебник за 9 одделение „Алгебра за 10 минути“
Задачата бр. 4 бара способност за решавање равенки од различни типови. Момци, треба да бидете добро упатени во методите за правилно решавање на квадратни равенки, фракциони рационални равенки и обични линеарни равенки. Треба да бидете добри и во извршување на операции со полиноми: множење и делење на полином со полином. Дали ви е потребна способност да ги изберете корените на равенката што се вклучени во областа на решението и да одредите кои корени треба да се исфрлат и да не се земат предвид?
Лекции кои ќе ви помогнат при подготовката на оваа задача:
1.Основни дефиниции и примери на решенија на линеарни функции.2. Поим и стандардна форма на моном.
3. Полином, стандардна форма, редукција, трансформација.
4. Примери за нумерички изрази. Алгебарски изрази со променливи и операции со нив.
5. Равенки, примери за решавање равенки.
6. Квадратни равенки. Лекција во тек.
7. Дробни рационални равенки. Лекција во тек.
8. Квадратен корен. Лекција во тек.
Ајде да продолжиме со анализа на примери на решенија.
Пример 1.
Најдете ги корените на равенката: $16x^2-1=0$.
Решение.
Забележете дека ни е дадена квадратна равенка, но не и целосна. Коефициентот x е нула. Потоа ќе се водиме според правилото: „ќе ги оставиме оние изрази во кои лево е х квадрат и ќе ги преместиме сите броеви надесно“.
Ајде да го трансформираме нашиот израз: $16x^2=1$.
Да ги поделиме двете страни на равенката со коефициентот x на квадрат: $x^2=\frac(1)(16)$.
За да ја решиме оваа равенка, потребно ни е знаење за квадратниот корен. Да го извлечеме коренот, не заборавајќи го тоа негативен бројмора да земеме предвид и: $x=±\sqrt(\frac(1)(16))=±\frac(1)(4)=±0,25$.
Одговор: $x=±0,25$.
Пример 2.
Решете ја равенката: $x^2=18-7x$.
Решение.
Да ги преместиме сите изрази на левата страна од равенката: $x^2+7x-18=0$.
Можеме да ја решиме вообичаената квадратна равенка на два начина:
1. „главно“, пресметување на дискриминаторот;
2. користејќи ја теоремата на Виет.
1 начин.
Да ги запишеме сите коефициенти за квадратната равенка: $a=1$, $b=7$, $c=-18$.
Да ја најдеме дискриминаторот: $D=b^2-4ac=(7)^2-4*1*(-18)=49+72=121=(11)^2>0$.
Откривме дека равенката има 2 корени.
Треба само да ги најдеме овие корени:
$x_1=\frac(-b+\sqrt(D))(2a)=\frac(-7+11)(2)=2$.
$x_2=\frac(-b-\sqrt(D))(2a)=\frac(-7-11)(2)=-9$.
Метод 2.
Да ја искористиме теоремата на Виет. Теоремата на Виет често го поедноставува решението на квадратните равенки многу пати, особено кога коефициентот $a=1$. Во овој случај, производот од корените на равенката е еднаков на коефициентот $c$, а збирот на корените на равенката е еднаков на минус коефициентот од $b$:
$x_1+x_2=-\frac(b)(a)$.
$x_1*x_2=\frac(c)(a)$.
Во нашиот пример, $с=-18$ и $b=7$. Почнуваме да подредуваме низ парови броеви чиј производ е еднаков на минус осумнаесет. Првите бројки што ми паѓаат на ум се девет и два. Откако ќе извршиме неколку едноставни множење и собирање, можеме да потврдиме дека корените $x=-9$ и $x=2$ се соодветни за нас.
$x_1*x_2=-9*2=-18=\frac(c)(a)$.
x$_1+x_2=-9+2=-7=-\frac(b)(a)$.
Одговор: $x=-9$, $x=2$.
Пример 3.
Решете ја равенката: $x-\frac(x)(7)=\frac(15)(7)$.
Решение.
Ни се дава вообичаеното линеарна равенкасо дробни коефициенти. За да ја решите оваа равенка треба правилно да работите со обичните дропки.
Првиот чекор е да се трансформира левата страна на равенката, поедноставувајќи ја: $x-\frac(x)(7)=\frac(7x)(7)-\frac(x)(7)=\frac(6x) ) (7) $.
Ја добивме равенката: $\frac(6x)(7)=\frac(15)(7)$.
Да ја поделиме десната страна на равенката со коефициентот x: $x=\frac(\frac(15)(7))(\frac(6)(7))$.
Да ја разгледаме поделбата одделно: $\frac(\frac(15)(7))(\frac(6)(7))=\frac(15)(7)*\frac(7)(6)=\frac( 15 )(6)=2\frac(3)(6)=2\frac(1)(2)=2,5$.
Добивме: $x=2,5$.
Одговор: $x=2,5$.
Пример 4.
Решете ја равенката: $(x+2)^2=(x-4)^2$.
Решение.
Метод 1.
Да ја користиме формулата за квадратот на збирот: $(x+2)^2=x^2+4x+4$.
$(x-4)^2=x^2-8x+16$.
Добивме: $x^2+4x+4=x^2-8x+16$.
Ајде да ја поедноставиме нашата равенка:
$x^2+4x-x^2+8x=16-4$.
$12x=$12.
$x=1$.
Метод 2.
За да ја решиме оваа равенка, можеме да ја користиме формулата за разлика од квадрати. $(x+2)^2-(x-4)^2=0$.
$(x+2+x-4)(x+2-x+4)=0$.
$(2x-2)*(6)=0$.
$2x-2=0$.
$2x=2$.
$x=1$.
Одговор: $x=1$.
Пример 5.
Решете ја равенката: $\frac(9)(x-14)=\frac(14)(x-9)$.
Решение.
Ние сме претставени фракциона рационална равенка. Кога ги решавате овие равенки, вреди да се запамети дека не можете да делите со нула. Затоа, корените на равенката секогаш треба да се проверуваат со нивна замена во именителот на првобитната равенка.
Да го користиме правилото за множење вкрстено по вкрстено: $9(x-9)=14(x-14)$.
Добивме линеарна равенка:
$9x-81=14x-196$.
$9x-14x=-196+81$.
$-5x=-115$.
$x=23$.
Откако го проверивме нашиот корен, убедени сме дека именителот на дропките од првобитната равенка не исчезнуваат.
Одговор: $x=23$.
Пример 6.
Најдете решенија што го задоволуваат системот: $\begin (случаи) x^2+9x-22=0, \\ x≤1 \end (случаи)$.
Решение.
Прво, да ја решиме квадратната равенка користејќи ја теоремата на Виет. Производот на нашите корени е 22$, а сумата е -9$.
Ајде да ги избереме корените:
$-11*2=-22$.
$-11+2=-9$.
Добивме два корени: $x_1=-11$ и $x_2=2$. Од овие корени, неравенката $x≤1$ ја задоволува првиот корен и тоа ќе биде одговорот.
Одговор: $x=-11$.
Пример 7.
Решете ја равенката: $23x-60-x^2=0$.
Во вашиот одговор наведете го модулот на разликата на корените.
Решение.
Да ја помножиме првобитната равенка со $-1$: $x^2-23x+60=0$.
Во оваа форма, равенката изгледа многу попозната.
Да ја искористиме теоремата на Виет и да ја претставиме нашата равенка како производ на биномите:
$(x-20)(x-3)=0$.
Добивме два корени $x_1=20$ и $x_2=3$.
Да го најдеме модулот на разликата: $|x_1-x_2|=|20-3|=|17|=17$.
Одговор: 17.
Пример 8.
Колку корени има равенката $x^6-x^2=0?$
Решение.
Да го извадиме најмалиот степен од заградите: $x^2(x^4-1)=0$.
Сега да ја искористиме формулата за разлика на квадрати:
$x^2 (x^2-1)(x^2+1)=0$.
И повторно да ја користиме истата формула:
$x^2 (x-1)(x+1)(x^2+1)=0$.
Оваа равенка е еквивалентна на множество равенки: Откривме дека оваа равенка има три корени.
Одговор: 3.
Пример 9.
Решете ја равенката: $\frac((x-2)(2x+1))(2-x)=0$.
Ако равенката има повеќе од еден корен, запишете го поголемиот како одговор.
Решение.
Оригиналната равенка е еквивалентна на следното множество:  Да ја решиме секоја равенка: Бидејќи именителот на дропката не може да биде еднаков на нула, едно решение се елиминира. Добивме еден корен од равенката $x=-0,5$.
Да ја решиме секоја равенка: Бидејќи именителот на дропката не може да биде еднаков на нула, едно решение се елиминира. Добивме еден корен од равенката $x=-0,5$.
Одговор: -0,5.
Александар Шабалин
Квадратни равенки се изучуваат во 8-мо одделение, така што тука нема ништо комплицирано. Способноста за нивно решавање е апсолутно неопходна.
Квадратна равенка е равенка од формата ax 2 + bx + c = 0, каде што коефициентите a, b и c се произволни броеви, а a ≠ 0.
Пред да истражите конкретни методи за решение, забележете дека сите квадратни равенкиможе да се подели во три класи:
- немаат корени;
- Имаат точно еден корен;
- Тие имаат два различни корени.
Ова е важна разлика помеѓу квадратните равенки и линеарните, каде коренот секогаш постои и е единствен. Како да се одреди колку корени има една равенка? Има една прекрасна работа за ова - дискриминаторски.
Дискриминаторски
Нека е дадена квадратната равенка ax 2 + bx + c = 0. Тогаш дискриминантот е едноставно бројот D = b 2 − 4ac.
Треба да ја знаете оваа формула напамет. Сега не е важно од каде доаѓа. Друга работа е важна: со знакот на дискриминатор можете да одредите колку корени има квадратната равенка. Имено:
- Ако Д< 0, корней нет;
- Ако D = 0, има точно еден корен;
- Ако D > 0, ќе има два корени.
Ве молиме запомнете: дискриминаторот го означува бројот на корените, а не нивните знаци, како што поради некоја причина веруваат многу луѓе. Погледнете ги примерите и сами ќе разберете се:
Задача. Колку корени имаат квадратните равенки:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Ајде да ги запишеме коефициентите за првата равенка и да ја најдеме дискриминаторот:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 1 12 = 64 − 48 = 16
Значи, дискриминантата е позитивна, па равенката има два различни корени. Ние ја анализираме втората равенка на сличен начин:
a = 5; b = 3; c = 7;
D = 3 2 − 4 5 7 = 9 − 140 = −131.
Дискриминаторката е негативна, нема корени. Последната равенка што остана е:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 1 9 = 36 − 36 = 0.
Дискриминаторот е нула - коренот ќе биде еден.
Ве молиме имајте предвид дека коефициентите се запишани за секоја равенка. Да, долго е, да, досадно е, но нема да ги мешате шансите и нема да правите глупави грешки. Изберете сами: брзина или квалитет.
Патем, ако се справите со тоа, по некое време нема да треба да ги запишувате сите коефициенти. Ќе правиш такви операции во главата. Повеќето луѓе почнуваат да го прават ова некаде по 50-70 решени равенки - генерално, не толку многу.
Корени на квадратна равенка
Сега да преминеме на самото решение. Ако дискриминантот D > 0, корените може да се најдат со помош на формулите:
Основна формула за корените на квадратна равенка
Кога D = 0, можете да користите која било од овие формули - ќе го добиете истиот број, што ќе биде одговорот. Конечно, ако Д< 0, корней нет — ничего считать не надо.
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Првата равенка:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 1 (−3) = 16.
D > 0 ⇒ равенката има два корени. Ајде да ги најдеме:
Втора равенка:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ равенката повторно има два корени. Ајде да ги најдеме
\[\begin(порамни) & ((x)_(1))=\frac(2+\sqrt(64))(2\cdot \left(-1 \десно))=-5; \\ & ((x)_(2))=\frac(2-\sqrt(64))(2\cdot \left(-1 \десно))=3. \\ \крај (порамни)\]
Конечно, третата равенка:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 1 36 = 0.
D = 0 ⇒ равенката има еден корен. Може да се користи која било формула. На пример, првиот:
Како што можете да видите од примерите, сè е многу едноставно. Ако ги знаете формулите и можете да броите, нема да има проблеми. Најчесто, се случуваат грешки при замена на негативни коефициенти во формулата. Повторно, техниката опишана погоре ќе помогне: погледнете ја формулата буквално, запишете го секој чекор - и многу наскоро ќе се ослободите од грешките.
Нецелосни квадратни равенки
Се случува квадратната равенка малку да се разликува од она што е дадено во дефиницијата. На пример:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Лесно е да се забележи дека на овие равенки им недостасува еден од поимите. Ваквите квадратни равенки се уште полесно да се решат од стандардните: тие дури и не бараат пресметување на дискриминаторот. Значи, да воведеме нов концепт:
Равенката ax 2 + bx + c = 0 се нарекува нецелосна квадратна равенка ако b = 0 или c = 0, т.е. коефициентот на променливата x или слободниот елемент е еднаков на нула.
Се разбира, можен е многу тежок случај кога двата од овие коефициенти се еднакви на нула: b = c = 0. Во овој случај, равенката има форма ax 2 = 0. Очигледно, таквата равенка има еден корен: x = 0.
Ајде да ги разгледаме останатите случаи. Нека b = 0, тогаш добиваме нецелосна квадратна равенка од формата ax 2 + c = 0. Да ја трансформираме малку:
Од аритметиката Квадратен коренпостои само од ненегативен број, последната еднаквост има смисла само за (−c /a) ≥ 0. Заклучок:
- Ако во нецелосна квадратна равенка од формата ax 2 + c = 0 неравенката (−c /a) ≥ 0 е исполнета, ќе има два корени. Формулата е дадена погоре;
- Ако (−c /a)< 0, корней нет.
Како што можете да видите, дискриминаторот не беше потребен - во нецелосни квадратни равенки нема сложени пресметки. Всушност, дури и не е неопходно да се запамети неравенката (−c /a) ≥ 0. Доволно е да се изрази вредноста x 2 и да се види што има од другата страна на знакот за еднаквост. Ако има позитивен број, ќе има два корени. Ако е негативен, корени воопшто нема да има.
Сега да ги погледнеме равенките од формата ax 2 + bx = 0, во кои слободниот елемент е еднаков на нула. Сè е едноставно овде: секогаш ќе има два корени. Доволно е да се факторизира полиномот:
Вадење на заедничкиот фактор од заградиПроизводот е нула кога барем еден од факторите е нула. Оттука потекнуваат корените. Како заклучок, да погледнеме неколку од овие равенки:
Задача. Решавање на квадратни равенки:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Нема корени, затоа што квадрат не може да биде еднаков на негативен број.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Наставник : Јургенсон Вероника Александровна
Класа: 9
Ставка: Алгебра
Тема на лекцијата: Подготвителна лекција за OGE во одделение 9 „Квадратни равенки“.
Фаза на обука на оваа тема : подготовка за OGE.
Тип на лекција: Час за генерализација и систематизација на знаењето
Цел:
Активност: Формирање на вештини на учениците за спроведување на регулаторни методи на дејствување.
Содржина: - увежбување методи за решавање квадратни равенки;
Развивање на способност за избор на најрационално решение;
Развојни: да се формираат клучните компетенции на учениците: информативни (способност да се анализираат информации, да се споредуваат, да се извлечат заклучоци), да се решаваат проблеми (способност да се поставуваат проблеми и, користејќи постојно знаење, да се најде излез од ситуацијата); комуникативен (способност за работа во групи, способност за слушање и слушање на другите, прифаќање на мислењата на другите)
Задачи за наставникот:
Да помогне во ажурирањето на знаењата на учениците за решавање на квадратни равенки;
Организирајте едукативни активности за вежбање начини за решавање на квадратни равенки;
Создадете услови за формирање на вештини за развој на способност за избор на најрационално решение;
Создадете услови за формирање на регулаторни UUD: поставување цели, самопочит и самоконтрола, планирање.
Технологија: Обука на повеќе нивоа
Наставни методи: Визуелен, вербален, метод на меѓусебна проверка, метод на заедничко изнаоѓање оптимално решение, привремена работа во групи, создавање проблемска ситуација, репродуктивна (упатство, илустрација, објаснување, практична обука). Методи на самоконтрола.
Користени форми на организација когнитивна активностстуденти:
Колективна форма на работа (фронтално испрашување, усна работа), групна, индивидуална работа (самостојна работа), работа во парови (меѓусебно испрашување).
Опрема и главни извори на информации:
Компјутер, проектор, екран, презентација за часот на тема „Методи на решавање квадратни равенки“.
Лист за перформанси за контрола и самоконтрола.
Картички-задачи за повеќестепена самостојна работа
Технолошка карта на часот:
Активностстудент
Организациски
Поздрав студентите
Поздрав на наставникот
Поставување на целите и задачите на часот. Мотивација едукативни активностиучениците
На последната сертификација, често има задачи каде што треба да бидете способни да решавате квадратни равенки.
Пренесување на целта на часот :
Денес во лекцијата ќе ги повториме, генерализираме и внесеме во системот изучените типови, методи и техники за решавање на квадратни равенки.
Врз основа на резултатите од нивната работа, односно според бројот на освоени бодови, секој ќе добие оценки.
Мото на лекцијата: „Мислиме, размислуваме, работиме и си помагаме едни на други“
(Слајд 2 ).
Наставниците слушаат.
Ажурирање на знаењето.
Момци, обично ја започнуваме лекцијата со проверка на домашната задача.
Кој ќе каже дека било потребно да се повторуваат за квадратните равенки?
Што се квадратни равенки?
Што се тие?
Кои методи за решавање на квадратни равенки ги знаете?
Наставниците одговараат на прашања и вршат самооценување на нивното знаење.
Генерализација и систематизација на знаењето
1. Улога на меѓусебна контрола.
Еве ги равенките (слајд 3)
x 2 + 7 x – 18 = 0;
2 x 2 + 1 = 0;
x 2 –2 x + 9 = 0;
2 y 2 – 3г + 1 = 0;
2 y 2 = 1;
–2 x 2 – x + 1 = 0;
x 2 + 6 x = 0;
4x 2 =0;
– x 2 – 6 x=1
2 x + x 2 – 1=0
На вашата маса има картичка со прашања на кои треба да одговорите (Прилог 1).
(слајд 4 ) Проверувајќи ги резултатите, разменете картички со вашиот сосед.
Одговори на прашања
2. Фронтална работа со одделението.
На(слајд 5) се пишуваат формули со елементи што недостасуваат. Задачата на часот е да открие што е оваа формула и што недостасува во снимањето на оваа формула.
Д = б ² – * а * .
Д > 0 , значи * корен.
Д * 0 , значи 1 корен.
Д * 0 , значи * корени.
Одговори на прашања
правилно знаење.
Решавајте равенки од картички. Еден од членовите на групата ќе го покаже решението на табла.
Споредете ги вашите одговори со точните, за секој точен одговор - 1 поен
Решавајте равенки
Објаснете го решението.
Фронтална работа со одделението
Кажи ми, дали можеш веднаш, без да правиш пресметки, да одговориш на моето прашање: „Колкав е збирот и производот на корените на квадратна равенка? (Едно лице на таблата ги запишува формулите на теоремата на Виета.)
(слајд 6)
Следна задача: вербално пронајдете го збирот и разликата на корените на равенката користејќи ја теоремата:
(одговори: 5 и 6; 9 и 20; -3 и 2) Вовед во техниката усна одлуканекои квадратни равенки.
Теоремата на Виета е широко користена во равенките на форматааX 2 + бx + c = 0.
Употребата на одредени својства дава значителни предности за брзо добивање одговори при решавање на квадратни равенки.
Ајде да ги разгледаме овие својства(слајд 7)
1) а + б+c = 0 x 1 = 1, x 2 = s/a.
5x 2 + 4x – 9 = 0; X 1 =1, x 2 = - 9/2.
2) а -б+ c = 0 x 1 = - 1, x 2 = - s/a.
На пример: 4x 2 + 11x + 7 = 0; X 1 = - 1, x 2 = - 7/4.
(слајд8)
3) а во + в 0
Решете ја равенката усно: x 2 + бx + ac = 0
Поделете ги неговите корени со a.
а) 2x 2 – 11x + 5 = 0.
Равенката ја решаваме усно: x 2 – 11x + 10 = 0. Неговите корени се 1 и 10. Поделете со 2.
Потоа x 1 = , x 2 = 5.
Одговор: ; 5.
(слајд 9)
в) 6x 2 –7х – 3 = 0
Равенката ја решаваме усно: x 2 –7x – 18 = 0. Неговите корени се -2 и 9. Поделете со 6.
Потоа x 1 = - , x 2 = .
Одговор: -; .
Одговори на прашања. Пополнете ги празнините во знаењето
Работете во групи на повеќе нивоа
Прием „Усогласеност“
Техника „фати грешка“.
Решавајте равенки користејќи ги овие својства(слајд 10)
Јасгрупа.1)најдете го збирот на корените на равенката
2x 2 – 3x + 1 = 0
2) Најдете го производот од корените на равенката
X 2 +9x +20 = 0
3) реши ја равенката
10x 2 – 8x - 2= 0
IIгрупа.
1)најдете го збирот и производот на корените на равенката
3x 2 – 8x + 5 = 0
Решавајте равенки
2) x 2 + 2x -24 = 0
3) 2 x 2 -7x +5 = 0
IIIгрупа
Решете ги проблемите:
1) x 2 +5x-6=0
2) 5x 2 -7x+2=0
3) 100x 2 -99x-199=0
Решавајте равенки
Проверете го решението.
Се врши корекција на знаењето.
2. Поврзете ги квадратните равенки и методите за нивно решавање:
(слајд 11)
2x 2 – 3x + 11 = 07 x 2 = 8x
X 2 – 10x + 100 = 0
X 2 –5x –6 = 0
– 2x 2 + x +14= 0
-факторизација
- општа формула на корените
-Теорема на Виета
3. Најдете грешки при решавање равенки =
Момците кои брзо ја завршуваат работата можат да решат дополнителна задача(слајд 14), напишано на табла.
По извршувањето, се врши брза проверка.(слајд 15)
Сега избројте го вкупниот број на поени и дајте си оценка.(слајд 16)
30-24 поени – оценка 5;
23-18 поени – резултат 4;
12-17 поени –. резултат 4
И секој добива оценка од наставникот за активност, храброст и истрајност. Па, ако некој денес не успеа да освои поени за позитивна оценка, тогаш успехот е уште пред вас, а следниот пат дефинитивно ќе биде со вас.
Решавајте равенки
спроведе самооценување.
Рефлексија.
Кој може да го каже она што го повторивме на час денес?
Дали ви се допадна како го направивме тоа?
Продолжете со фразите:
Сега знам со сигурност...
Разбирам …
Научив …
Мое мислење …
Секој има обоени картички на масата.
Ако сте среќни и задоволни од лекцијата, подигнете зелен картон.
Ако лекцијата е интересна и сте работеле активно, кревате жолт картон.
спроведе самооценување.
(слајд 17) Решавајте равенки од збирката задачи
Државна конечна сертификација
Матуранти од 9-то одделение.
А.В. Семенов, А.С.Трепалин, И.В.Јашченко
по нивоа
Изберете задачи според вашето ниво
! Од теорија до пракса;
! Од едноставни до сложени
MAOU "Средно училиште Платошин",
наставник по математика, Мелехина Г.В.

Општа форма на линеарна равенка: секира + б = 0 ,
Каде аИ б– бројки (коефициенти).
- Ако a = 0И b = 0, Тоа 0x + 0 = 0 – бесконечно многу корени;
- Ако a = 0И b ≠ 0, Тоа 0x + b = 0– нема решенија;
- Ако a ≠ 0И б = 0 , Тоа секира + 0 = 0 – еден корен, x = 0;
- Ако a ≠ 0И б ≠ 0 , Тоа секира + б = 0 - еден корен,
! Ако X е на првата сила и не е во именителот, тогаш тоа е линеарна равенка

! И ако линеарната равенка е комплекс :
! Условите со X одат налево, без X - надесно.

! Овие равенки се исто така линеарна .
! Главното својство на пропорција (напречно).
! Отворете ги заградите, со X налево, без X надесно.


- ако коефициентот a = 1, тогаш се повикува равенката дадена :
- ако коефициентот б = 0 или/и c = 0, тогаш се повикува равенката нецелосни :

! Основни формули
! Повеќе формули


Биквадратна равенка- наречена равенка на формата секира 4 +bx 2 + c = 0 .
Биквадратната равенка се сведува на квадратна равенкакористејќи замена, тогаш
Добиваме квадратна равенка:
Ајде да ги најдеме корените и да се вратиме на замената:

Пример 1:
Решете ја равенката x 4 + 5x 2 – 36 = 0.
Решение:
Замена: x 2 = t.
t 2 + 5t – 36 = 0. Корените на равенката се t 1 = -9 и t 2 = 4.
x 2 = -9 или x 2 = 4.
Одговор: Во првата равенка нема корени, но во втората: x = ±2.
Пример 2:
Решете ја равенката (2х – 1) 4 – 25 (2x – 1) 2 + 144 = 0.
Решение:
Замена: (2x – 1) 2 = t.
t 2 – 25t + 144 = 0. Корените на равенката се t 1 = 9 и t 2 = 16.
(2x – 1) 2 = 9 или (2x – 1) 2 = 16.
2x – 1 = ±3 или 2x – 1 = ±4.
Првата равенка има два корени: x = 2 и x = -1, втората исто така има два корени: x = 2,5 и x = -1,5.
Одговор: -1,5; -1; 2; 2.5.

1) X 4 - 9 X 2 = 0; 2) 4 X 4 - x 2 = 0;
1) X 4 + x 2 - 2 = 0;
2) X 4 - 3 X 2 - 4 = 0; 3) 9 X 4 + 8 X 2 - 1 = 0; 4) 20 X 4 - X 2 - 1 = 0.

Решавајте равенки со избирање од левата страна полн квадрат :
1) X 4 - 20 X 2 + 64 = 0; 2) X 4 - 13 X 2 + 36 = 0; 3) X 4 - 4 X 2 + 1 = 0; 4) X 4 + 2 X 2 +1 = 0.
! Запомнете го квадратот на збирот и квадратот на разликата

Рационално изразувањее алгебарски израз составен од броеви и променлива xкористејќи ги операциите собирање, одземање, множење, делење и степенување со природен показател.
Ако r(x) - рационално изразување, потоа равенката r(x)=0наречена рационална равенка.
Алгоритам за решавање на рационална равенка:
1. Поместете ги сите членови од равенката на едната страна.
2. Претворете го овој дел од равенката во форма алгебарска дропка p(x)/q(x)
3. Решете ја равенката p(x)=0
4. За секој корен од равенката p(x)=0проверете дали го задоволува условот q(x)≠0или не. Ако да, тогаш ова е коренот дадена равенка; ако не, тогаш тоа е надворешен корен и не треба да се вклучува во одговорот.

! Да се потсетиме на решението на фракционата рационална равенка:

! За да се решат равенките, корисно е да се потсетиме на скратените формули за множење:


Ако равенката содржи променлива под знакот на квадратен корен, тогаш равенката се нарекува ирационален .
Начин на квадратура на двете страни на равенката- главниот метод за решавање на ирационални равенки.
Откако ќе ја решите добиената рационална равенка, неопходно е да провери , отстранување на можните надворешни корени.

Одговор: 5; 4
Друг пример:
Испитување:
Изразот нема значење.
Одговор:нема решенија.


Во терминот „квадратна равенка“, клучниот збор е „квадратна“. Ова значи дека равенката нужно мора да содржи променлива (иста х) на квадрат и не треба да има xes до третата (или поголема) моќност.
Решението на многу равенки се сведува на решавање на квадратни равенки.
Ајде да научиме да утврдиме дека ова е квадратна равенка, а не некоја друга равенка.
Пример 1.
Ајде да се ослободиме од именителот и да го помножиме секој член од равенката со
Ајде да преместиме сè на левата страна и да ги подредиме поимите по опаѓачки редослед на силите на X
Сега можеме со сигурност да кажеме дека оваа равенка е квадратна!
Пример 2.
Помножете ја левата и десната страна со:
Оваа равенка, иако првично беше во неа, не е квадратна!
Пример 3.
Ајде да помножиме сè со:
Страшно? Четвртиот и вториот степен... Меѓутоа, ако направиме замена, ќе видиме дека имаме едноставна квадратна равенка:
Пример 4.
Се чини дека е таму, но ајде да погледнеме подетално. Ајде да преместиме сè на левата страна:
Видете, тоа е намалено - и сега тоа е едноставна линеарна равенка!
Сега обидете се сами да одредите кои од следните равенки се квадратни, а кои не се:
Примери:
Одговори:
- квадрат;
- квадрат;
- не квадрат;
- не квадрат;
- не квадрат;
- квадрат;
- не квадрат;
- квадрат.
Математичарите конвенционално ги делат сите квадратни равенки на следниве типови:
- Целосни квадратни равенки- равенки во кои коефициентите и, како и слободен член c не се еднакви на нула (како во примерот). Покрај тоа, меѓу целосните квадратни равенки постојат дадена- ова се равенки во кои коефициентот (равенката од примерот еден не само што е целосна, туку и намалена!)
- Нецелосни квадратни равенки- равенки во кои коефициентот и или слободниот член c се еднакви на нула:
Тие се нецелосни бидејќи им недостасува некој елемент. Но, равенката секогаш мора да содржи x квадрат!!! Во спротивно веќе нема да биде квадратна равенка, туку некоја друга равенка.
Зошто дошле до ваква поделба? Се чини дека има X квадрат, и во ред. Оваа поделба се одредува со методите на решение. Ајде да погледнеме во секоја од нив подетално.
Решавање на нецелосни квадратни равенки
Прво, да се фокусираме на решавање на нецелосни квадратни равенки - тие се многу поедноставни!
Постојат типови на нецелосни квадратни равенки:
- , во оваа равенка коефициентот е еднаков.
- , во оваа равенка слободниот член е еднаков на.
- , во оваа равенка коефициентот и слободниот член се еднакви.
1. јас. Бидејќи знаеме да го земеме квадратниот корен, ајде да изразиме од оваа равенка
Изразот може да биде или негативен или позитивен. Квадратен број не може да биде негативен, затоа што при множење на два негативни или два позитивни броја, резултатот секогаш ќе биде позитивен број, така што: ако, тогаш равенката нема решенија.
И ако, тогаш добиваме два корени. Нема потреба да ги меморирате овие формули. Главната работа е дека мора да знаете и секогаш да запомните дека не може да биде помалку.
Ајде да се обидеме да решиме неколку примери.
Пример 5:
Решете ја равенката
Сега останува само да се извлече коренот од левата и десната страна. На крајот на краиштата, се сеќавате како да извлечете корени?
Одговор:
Никогаш не заборавајте за корените со негативен знак!!!
Пример 6:
Решете ја равенката
Одговор:
Пример 7:
Решете ја равенката
О! Квадратот на број не може да биде негативен, што значи дека равенката
без корени!
За такви равенки кои немаат корени, математичарите излегоа со посебна икона - (празен сет). А одговорот може да се напише вака:
Одговор:
Така, оваа квадратна равенка има два корени. Овде нема ограничувања, бидејќи не го извадивме коренот.
Пример 8:
Решете ја равенката
Да го извадиме заедничкиот фактор од загради:
Така,
Оваа равенка има два корени.
Одговор:
Наједноставниот тип на нецелосни квадратни равенки (иако сите се едноставни, нели?). Очигледно, оваа равенка секогаш има само еден корен:
Овде ќе се откажеме од примери.
Решавање на целосни квадратни равенки
Потсетуваме дека целосна квадратна равенка е равенка на формата равенка каде
Решавањето на целосни квадратни равенки е малку потешко (само малку) од овие.
Запомнете, Секоја квадратна равенка може да се реши со помош на дискриминатор! Дури и нецелосни.
Останатите методи ќе ви помогнат да го направите тоа побрзо, но ако имате проблеми со квадратните равенки, прво совладајте го решението користејќи ја дискриминаторот.
1. Решавање на квадратни равенки со помош на дискриминант.
Решавањето на квадратните равенки со помош на овој метод е многу едноставно; главната работа е да се запамети низата на дејства и неколку формули.
Ако, тогаш равенката има корен.Треба да обрнете посебно внимание на чекорот. Дискриминантот () ни го кажува бројот на корените на равенката.
- Ако, тогаш формулата во чекорот ќе се сведе на. Така, равенката ќе има само корен.
- Ако, тогаш нема да можеме да го извлечеме коренот на дискриминаторот на чекорот. Ова покажува дека равенката нема корени.
Да се вратиме на нашите равенки и да погледнеме неколку примери.
Пример 9:
Решете ја равенката
Чекор 1прескокнуваме.
Чекор 2.
Го наоѓаме дискриминаторот:
Ова значи дека равенката има два корени.
Чекор 3.
Одговор:
Пример 10:
Решете ја равенката
Равенката е претставена во стандардна форма, па Чекор 1прескокнуваме.
Чекор 2.
Го наоѓаме дискриминаторот:
Ова значи дека равенката има еден корен.
Одговор:
Пример 11:
Решете ја равенката
Равенката е претставена во стандардна форма, па Чекор 1прескокнуваме.
Чекор 2.
Го наоѓаме дискриминаторот:
Ова значи дека нема да можеме да го извлечеме коренот на дискриминаторот. Нема корени на равенката.
Сега знаеме како правилно да ги запишеме таквите одговори.
Одговор:без корени
2. Решавање на квадратни равенки со помош на теоремата на Виета.
Ако се сеќавате, постои еден вид равенка што се нарекува намалена (кога коефициентот a е еднаков на):
Ваквите равенки се многу лесно да се решат користејќи ја теоремата на Виета:
Збир на корени даденаквадратната равенка е еднаква, а производот на корените е еднаков.
Пример 12:
Решете ја равенката
Оваа равенка може да се реши со помош на теоремата на Виета бидејќи .
Збирот на корените на равенката е еднаков, т.е. ја добиваме првата равенка:
И производот е еднаков на:
Ајде да го составиме и решиме системот:
- И. Износот е еднаков на;
- И. Износот е еднаков на;
- И. Износот е еднаков.
и се решение за системот:
Одговор: ; .
Пример 13:
Решете ја равенката
Одговор:
Пример 14:
Решете ја равенката
Равенката е дадена, што значи:
Одговор:
КВАДРАТСКИ РАВЕНКИ. ПРОСЕЧНО НИВО
Што е квадратна равенка?
Со други зборови, квадратна равенка е равенка на формата, каде што - непознатото, - некои броеви и.
Бројот се нарекува највисок или првиот коефициентквадратна равенка, - втор коефициент, А - слободен член.
Зошто? Затоа што ако равенката веднаш стане линеарна, затоа што ќе исчезне.
Во овој случај, и може да биде еднаква на нула. Во овој стол равенката се нарекува нецелосна. Ако сите поими се на место, односно равенката е завршена.
Решенија на различни типови квадратни равенки
Методи за решавање на нецелосни квадратни равенки:
Прво, да ги погледнеме методите за решавање на нецелосни квадратни равенки - тие се поедноставни.
Можеме да ги разликуваме следниве видови равенки:
I., во оваа равенка коефициентот и слободниот член се еднакви.
II. , во оваа равенка коефициентот е еднаков.
III. , во оваа равенка слободниот член е еднаков на.
Сега да го погледнеме решението за секој од овие подтипови.
Очигледно, оваа равенка секогаш има само еден корен:
Квадратен број не може да биде негативен, бидејќи кога ќе помножите два негативни или два позитивни броја, резултатот секогаш ќе биде позитивен број. Затоа:
ако, тогаш равенката нема решенија;
ако имаме два корени
Нема потреба да ги меморирате овие формули. Главната работа што треба да се запамети е дека не може да биде помала.
Примери:
Решенија:
Одговор:
Никогаш не заборавајте за корените со негативен знак!
Квадратот на број не може да биде негативен, што значи дека равенката
без корени.
За накратко да запишеме дека проблемот нема решенија, ја користиме иконата за празно поставување.
Одговор:
Значи, оваа равенка има два корени: и.
Одговор:
Да го извадиме заедничкиот фактор од загради:
Производот е еднаков на нула ако барем еден од факторите е еднаков на нула. Ова значи дека равенката има решение кога:
Значи, оваа квадратна равенка има два корени: и.
Пример:
Решете ја равенката.
Решение:
Да ја пресметаме левата страна на равенката и да ги најдеме корените:
Одговор:
Методи за решавање на целосни квадратни равенки:
1. Дискриминаторски
Решавањето на квадратните равенки на овој начин е лесно, главната работа е да се запамети низата на дејства и неколку формули. Запомнете, секоја квадратна равенка може да се реши со помош на дискриминатор! Дури и нецелосни.
Дали го забележавте коренот од дискриминантот во формулата за корени? Но, дискриминаторот може да биде негативен. Што да се прави? Треба да обрнеме посебно внимание на чекор 2. Дискриминаторот ни го кажува бројот на корените на равенката.
- Ако, тогаш равенката има корени:
- Ако, тогаш равенката има исти корени, а всушност, еден корен:
Таквите корени се нарекуваат двојни корени.
- Ако, тогаш коренот на дискриминантот не е извлечен. Ова покажува дека равенката нема корени.
Зошто е можно различни количиникорени? Да се свртиме кон геометриска смислаквадратна равенка. Графикот на функцијата е парабола:

Во посебен случај, кој е квадратна равенка, . Ова значи дека корените на квадратната равенка се точките на пресек со оската на апсцисата (оската). Параболата може воопшто да не ја пресекува оската или може да ја пресече на една (кога темето на параболата лежи на оската) или две точки.
Покрај тоа, коефициентот е одговорен за насоката на гранките на параболата. Ако, тогаш гранките на параболата се насочени нагоре, а ако, тогаш надолу.
Примери:
Решенија:
Одговор:
Одговор:.
Одговор:
Ова значи дека нема решенија.
Одговор:.
2. Теорема на Виета
Многу е лесно да се користи теоремата на Виета: само треба да изберете пар броеви чиј производ е еднаков на слободниот член на равенката, а збирот е еднаков на вториот коефициент земен со спротивен знак.
Важно е да се запамети дека теоремата на Виета може да се примени само во намалени квадратни равенки ().
Ајде да погледнеме неколку примери:
Пример #1:
Решете ја равенката.
Решение:
Оваа равенка може да се реши со помош на теоремата на Виета бидејќи . Други коефициенти: ; .
Збирот на корените на равенката е:
И производот е еднаков на:
Ајде да избереме парови на броеви чиј производ е еднаков и да провериме дали нивниот збир е еднаков:
- И. Износот е еднаков на;
- И. Износот е еднаков на;
- И. Износот е еднаков.
и се решение за системот:
Така, и се корените на нашата равенка.
Одговор: ; .
Пример #2:
Решение:
Ајде да избереме парови на броеви што даваат во производот, а потоа да провериме дали нивниот збир е еднаков:
и: вкупно даваат.
и: вкупно даваат. За да се добие, доволно е едноставно да се сменат знаците на наводните корени: и, на крајот на краиштата, производот.
Одговор:
Пример #3:
Решение:
Слободниот член на равенката е негативен, и затоа производот на корените е негативен број. Ова е можно само ако еден од корените е негативен, а другиот е позитивен. Затоа збирот на корените е еднаков на разлики во нивните модули.
Дозволете ни да избереме парови на броеви кои даваат во производот, а чија разлика е еднаква на:
и: нивната разлика е еднаква - не одговара;
и: - не е соодветно;
и: - не е соодветно;
и: - погоден. Останува само да се запамети дека еден од корените е негативен. Бидејќи нивниот збир мора да биде еднаков, коренот со помал модул мора да биде негативен: . Проверуваме:
Одговор:
Пример #4:
Решете ја равенката.
Решение:
Равенката е дадена, што значи:
Слободниот член е негативен, и затоа производот на корените е негативен. И ова е можно само кога едниот корен од равенката е негативен, а другиот позитивен.
Ајде да избереме парови чиј производ е еднаков, а потоа да одредиме кои корени треба да имаат негативен знак:
Очигледно, само корените се погодни за првиот услов:
Одговор:
Пример #5:
Решете ја равенката.
Решение:
Равенката е дадена, што значи:
Збирот на корените е негативен, што значи дека барем еден од корените е негативен. Но, бидејќи нивниот производ е позитивен, тоа значи дека двата корени имаат знак минус.
Дозволете ни да избереме парови на броеви чиј производ е еднаков на:
Очигледно, корените се броевите и.
Одговор:
Се согласувам, многу е погодно да се дојде до корени усно, наместо да се брои овој гаден дискриминатор. Обидете се да ја користите теоремата на Виета што е можно почесто.
Но, теоремата на Виета е потребна за да се олесни и забрза пронаоѓањето на корените. За да имате корист од неговото користење, мора да ги доведете дејствата до автоматизам. И за ова, решете уште пет примери. Но, не изневерувајте: не можете да користите дискриминатор! Само теоремата на Виета:
Решенија за задачи за самостојна работа:
Задача 1. ((x)^(2))-8x+12=0
Според теоремата на Виета:
Како и обично, изборот го започнуваме со парчето:
Не е погоден бидејќи износот;
: износот е токму она што ви треба.
Одговор: ; .
Задача 2.
И повторно нашата омилена теорема Виета: збирот мора да биде еднаков, а производот мора да биде еднаков.
Но бидејќи не смее, туку, ги менуваме знаците на корените: и (вкупно).
Одговор: ; .
Задача 3.
Хм... Каде е тоа?
Треба да ги преместите сите термини во еден дел:
Збирот на корените е еднаков на производот.
Добро, застани! Равенката не е дадена. Но, теоремата на Виета е применлива само во дадените равенки. Значи, прво треба да дадете равенка. Ако не можете да водите, откажете се од оваа идеја и решете ја на друг начин (на пример, преку дискриминатор). Дозволете ми да ве потсетам дека да се даде квадратна равенка значи да се направи водечки коефициент еднаков:
Одлично. Тогаш збирот на корените е еднаков на и производот.
Овде е лесно да се избере како лупење круши: на крајот на краиштата, тоа е прост број (извинете за тавтологијата).
Одговор: ; .
Задача 4.
Слободниот член е негативен. Што е посебно за ова? И факт е дека корените ќе имаат различни знаци. И сега, при изборот, не го проверуваме збирот на корените, туку разликата во нивните модули: оваа разлика е еднаква, но производ.
Значи, корените се еднакви на и, но еден од нив е минус. Теоремата на Виета ни кажува дека збирот на корените е еднаков на вториот коефициент со спротивен знак, т.е. Ова значи дека помалиот корен ќе има минус: и, бидејќи.
Одговор: ; .
Задача 5.
Што треба прво да направите? Така е, дајте ја равенката:
Повторно: ги избираме факторите на бројот, а нивната разлика треба да биде еднаква на:
Корените се еднакви на и, но еден од нив е минус. Кои? Нивниот збир треба да биде еднаков, што значи дека минусот ќе има поголем корен.
Одговор: ; .
Дозволете ми да резимирам:
- Теоремата на Виета се користи само во дадените квадратни равенки.
- Користејќи ја теоремата на Виета, можете да ги најдете корените со избор, усно.
- Ако равенката не е дадена или не се најде соодветен пар фактори од слободниот член, тогаш нема цели корени и треба да го решите на друг начин (на пример, преку дискриминатор).
3. Метод за избор на целосен квадрат
Ако сите поими што ја содржат непознатата се претставени во форма на поими од скратените формули за множење - квадратот на збирот или разликата - тогаш по замена на променливите, равенката може да се претстави во форма на нецелосна квадратна равенка од типот.
На пример:
Пример 1:
Решете ја равенката: .
Решение:
Одговор:
Пример 2:
Решете ја равенката: .
Решение:
Одговор:
Во принцип, трансформацијата ќе изгледа вака:
Ова имплицира:.
Не те потсетува на ништо? Ова е дискриминаторска работа! Токму така ја добивме формулата за дискриминација.
КВАДРАТСКИ РАВЕНКИ. НАКРАТКО ЗА ГЛАВНИТЕ РАБОТИ
Квадратна равенка- ова е равенка на формата, каде што - непознатото, - коефициентите на квадратната равенка, - слободниот член.
Целосна квадратна равенка- равенка во која коефициентите не се еднакви на нула.
Намалена квадратна равенка- равенка во која коефициентот, односно: .
Нецелосна квадратна равенка- равенка во која коефициентот и или слободниот член c се еднакви на нула:
- ако коефициентот, равенката изгледа вака:
- ако има слободен член, равенката има форма: ,
- ако и, равенката изгледа вака: .
1. Алгоритам за решавање на нецелосни квадратни равенки
1.1. Нецелосна квадратна равенка на формата, каде што, :
1) Да го изразиме непознатото:
2) Проверете го знакот на изразот:
- ако, тогаш равенката нема решенија,
- ако, тогаш равенката има два корени.
1.2. Нецелосна квадратна равенка на формата, каде што, :
1) Да го извадиме заедничкиот фактор од загради: ,
2) Производот е еднаков на нула ако барем еден од факторите е еднаков на нула. Според тоа, равенката има два корени:
1.3. Нецелосна квадратна равенка на формата, каде што:
Оваа равенка секогаш има само еден корен: .
2. Алгоритам за решавање на целосни квадратни равенки од формата каде
2.1. Решение со помош на дискриминант
1) Да ја доведеме равенката во стандардна форма: ,
2) Да ја пресметаме дискриминаторот користејќи ја формулата: , која го означува бројот на корените на равенката:
3) Најдете ги корените на равенката:
- ако, тогаш равенката има корени, кои се наоѓаат со формулата:
- ако, тогаш равенката има корен, кој се наоѓа со формулата:
- ако, тогаш равенката нема корени.
2.2. Решение со помош на теоремата на Виета
Збирот на корените на намалената квадратна равенка (равенка на формата каде) е еднаков, а производот на корените е еднаков, т.е. , А.
2.3. Решение со методот на избор на целосен квадрат
Ако квадратната равенка на формата има корени, тогаш може да се запише во форма: .
Па, темата заврши. Ако ги читате овие редови, тоа значи дека сте многу кул.
Затоа што само 5% од луѓето се способни да совладаат нешто сами. И ако читате до крај, тогаш сте во овие 5%!
Сега најважното нешто.
Ја разбравте теоријата на оваа тема. И, повторувам, ова... ова е само супер! Веќе сте подобри од огромното мнозинство ваши врсници.
Проблемот е што ова можеби не е доволно...
За што?
За успешно завршувањеУнифициран државен испит, за прием на факултет со буџет и, НАЈВАЖНО, доживотно.
Нема да те убедам во ништо, само едно ќе кажам...
Луѓе кои примиле добро образование, заработуваат многу повеќе од оние кои не го добиле. Ова е статистика.
Но, ова не е главната работа.
Главната работа е што тие се ПОСРЕЌНИ (има такви студии). Можеби затоа што многу повеќе можности се отвораат пред нив и животот станува посветол? Не знам...
Но, размислете сами...
Што е потребно за да бидете сигурни дека ќе бидете подобри од другите на Единствениот државен испит и на крајот да бидете... посреќни?
ДОБИЈТЕ РАКА СО РЕШАВАЊЕ ПРОБЛЕМИ НА ОВАА ТЕМА.
Нема да ве прашаат за теорија за време на испитот.
Ќе ви треба решаваат проблеми наспроти времето.
И, ако не сте ги решиле (МНОГУ!), дефинитивно ќе направите глупава грешка некаде или едноставно нема да имате време.
Тоа е како во спортот - треба да го повторите многу пати за да победите сигурно.
Најдете ја колекцијата каде што сакате, нужно со решенија, детална анализа и одлучи, одлучува, одлучува!
Можете да ги користите нашите задачи (опционално) и ние, се разбира, ги препорачуваме.
Со цел да се подобрите во користењето на нашите задачи, треба да помогнете да го продолжите животниот век на учебникот YouClever што моментално го читате.
Како? Постојат две опции:
- Отклучете ги сите скриени задачи во оваа статија -
- Отклучете го пристапот до сите скриени задачи во сите 99 статии од учебникот - Купете учебник - 899 RUR
Да, имаме 99 вакви статии во нашиот учебник и пристапот до сите задачи и сите скриени текстови во нив може веднаш да се отвори.
Пристап до сите скриени задачи е обезбеден за ЦЕЛИОТ век на траење на страницата.
Во заклучок...
Ако не ви се допаѓаат нашите задачи, најдете други. Само не застанувај на теорија.
„Разбрано“ и „Можам да решам“ се сосема различни вештини. Ви требаат и двете.
Најдете проблеми и реши ги!