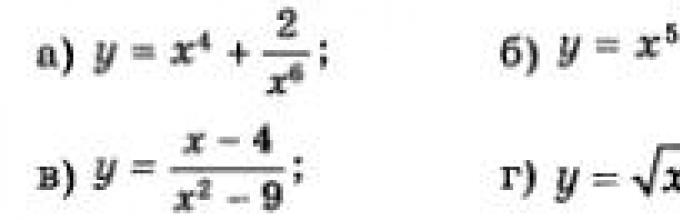Кои ви беа познати до еден или друг степен. Таму беше забележано и дека залихите на функционалните својства постепено ќе се надополнуваат. Две нови својства ќе бидат разгледани во овој дел.
Дефиниција 1.
Функцијата y = f(x), x є X, се повикува дури и ако за која било вредност x од множеството X важи еднаквоста f (-x) = f (x).
Дефиниција 2.
Функцијата y = f(x), x є X, се нарекува непарна ако за која било вредност x од множеството X важи еднаквоста f (-x) = -f (x).
Докажете дека y = x 4 е парна функција.
Решение. Имаме: f(x) = x 4, f(-x) = (-x) 4. Но (-x) 4 = x 4. Тоа значи дека за секој x важи еднаквоста f(-x) = f(x), т.е. функцијата е рамномерна.
Слично, може да се докаже дека функциите y - x 2, y = x 6, y - x 8 се парни.
Докажете дека y = x 3 ~ непарна функција.
Решение. Имаме: f(x) = x 3, f(-x) = (-x) 3. Но (-x) 3 = -x 3. Тоа значи дека за секој x важи еднаквоста f (-x) = -f (x), т.е. функцијата е непарна.
Слично, може да се докаже дека функциите y = x, y = x 5, y = x 7 се непарни.
Јас и ти веќе не еднаш сме се увериле дека новите поими во математиката најчесто имаат „земно“ потекло, т.е. може некако да се објаснат. Ова е случај и со парните и со непарните функции. Види: y - x 3, y = x 5, y = x 7 се непарни функции, додека y = x 2, y = x 4, y = x 6 се парни функции. И воопшто, за која било функција од формата y = x" (подолу конкретно ќе ги проучуваме овие функции), каде што n е природен број, можеме да заклучиме: ако n - чуден број, тогаш функцијата y = x" е непарна; ако n е парен број, тогаш функцијата y = xn е парна.
Има и функции кои не се ниту парни ниту непарни. Таква, на пример, е функцијата y = 2x + 3. Навистина, f(1) = 5, и f (-1) = 1. Како што можете да видите, овде, значи, ниту идентитетот f(-x) = f ( x), ниту идентитетот f(-x) = -f(x).
Значи, функцијата може да биде парна, непарна или ниту една.
Проучувајќи го прашањето дали дадена функцијапарни или непарни обично се нарекува проучување на функција за паритет.
Дефинициите 1 и 2 се однесуваат на вредностите на функцијата во точките x и -x. Ова претпоставува дека функцијата е дефинирана и во точката x и во точката -x. Тоа значи дека точката -x припаѓа на доменот на дефинирање на функцијата истовремено со точката x. Ако множество на броеви X, заедно со секој од неговите елементи x, го содржи и спротивниот елемент -x, тогаш X се нарекува симетрично множество. Да речеме, (-2, 2), [-5, 5], (-oo, +oo) се симетрични множества, додека \).
Бидејќи \(x^2\geqslant 0\) , тогаш левата страна на равенката (*) е поголема или еднаква на \(0+ \mathrm(tg)^2\,1\) .
Така, еднаквоста (*) може да биде вистинита само кога двете страни на равенката се еднакви на \(\mathrm(tg)^2\,1\) . И ова значи дека \[\почеток(случаи) 2x^2+\mathrm(tg)^2\,1=\mathrm(tg)^2\,1 \\ \mathrm(tg)\,1\cdot \mathrm(tg)\ ,(\cos x)=\mathrm(tg)^2\,1 \end (случаи) \quad\Leftrightarrow\quad \begin(scases) x=0\\ \mathrm(tg)\,(\cos x) =\mathrm(tg)\,1 \end (случаи)\quad\Leftright стрелка\quad x=0\]Според тоа, вредноста \(a=-\mathrm(tg)\,1\) ни одговара.
Одговор:
\(a\in \(-\mathrm(tg)\,1;0\)\)
Задача 2 #3923
Ниво на задача: еднакво на обединетиот државен испит
Најдете ги сите вредности на параметарот \(a\), за секоја од нив графикот на функцијата \
симетрични во однос на потеклото.
Ако графикот на функцијата е симетричен во однос на потеклото, тогаш таквата функција е непарна, односно \(f(-x)=-f(x)\) важи за кое било \(x\) од доменот на дефинирање на функцијата. Така, потребно е да се најдат оние вредности на параметрите за кои \(f(-x)=-f(x).\)
\[\почеток(порамнет) &3\mathrm(tg)\,\left(-\dfrac(ax)5\десно)+2\sin \dfrac(8\pi a+3x)4= -\left(3\ mathrm(tg)\,\left(\dfrac(ax)5\right)+2\sin \dfrac(8\pi a-3x)4\right)\quad \Rightarrow\quad -3\mathrm(tg)\ ,\dfrac(ax)5+2\sin \dfrac(8\pi a+3x)4= -\left(3\mathrm(tg)\,\left(\dfrac(ax)5\десно)+2\ sin \dfrac(8\pi a-3x)4\десно) \quad \Rightarrow\\ \Rightarrow\quad &\sin \dfrac(8\pi a+3x)4+\sin \dfrac(8\pi a- 3x)4=0 \quad \Десна стрелка \quad2\sin \dfrac12\left(\dfrac(8\pi a+3x)4+\dfrac(8\pi a-3x)4\десно)\cdot \cos \dfrac12 \left(\dfrac(8\pi a+3x)4-\dfrac(8\pi a-3x)4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \ frac34 x=0 \end (порамнет)\]
Последната равенка мора да биде исполнета за сите \(x\) од доменот на \(f(x)\), затоа, \(\sin(2\pi a)=0 \Десна стрелка a=\dfrac n2, n\in\mathbb(Z)\).
Одговор:
\(\dfrac n2, n\in\mathbb(Z)\)
Задача 3 #3069
Ниво на задача: еднакво на обединетиот државен испит
Најдете ги сите вредности на параметарот \(a\), за секоја од нив равенката \ има 4 решенија, каде што \(f\) е парна периодична функција со период \(T=\dfrac(16)3\) дефинирано на целата бројна линија , и \(f(x)=ax^2\) за \(0\leqslant x\leqslant \dfrac83.\)
(Задача од претплатници)
Задача 4 #3072
Ниво на задача: еднакво на обединетиот државен испит
Најдете ги сите вредности на \(a\) , од кои за секоја равенката \
има барем еден корен.
(Задача од претплатници)
Ајде да ја преработиме равенката во форма \
и разгледајте две функции: \(g(x)=7\sqrt(2x^2+49)\) и \(f(x)=3|x-7a|-6|x|-a^2+7a\ ) .
Функцијата \(g(x)\) е парна и има минимална точка \(x=0\) (и \(g(0)=49\) ).
Функцијата \(f(x)\) за \(x>0\) се намалува, а за \(x<0\)
– возрастающей, следовательно, \(x=0\)
– точка максимума.
Навистина, кога \(x>0\) вториот модул ќе се отвори позитивно (\(|x|=x\)), затоа, без оглед на тоа како ќе се отвори првиот модул, \(f(x)\) ќе биде еднаков до \( kx+A\) , каде што \(A\) е изразот на \(a\) и \(k\) е еднаков на \(-9\) или \(-3\) . Кога \(x<0\)
наоборот: второй модуль раскроется отрицательно и \(f(x)=kx+A\)
, где \(k\)
равно либо \(3\)
, либо \(9\)
.
Ајде да ја најдеме вредноста на \(f\) во максималната точка: \ 
За да може равенката да има барем едно решение, потребно е графиците на функциите \(f\) и \(g\) да имаат барем една пресечна точка. Затоа, ви треба: \ Решавајќи го овој сет на системи, го добиваме одговорот: \\]
Одговор:
\(а\во \(-7\)\чаша\)
Задача 5 #3912
Ниво на задача: еднакво на обединетиот државен испит
Најдете ги сите вредности на параметарот \(a\), од кои секоја равенка \
има шест различни решенија.
Да ја направиме замената \((\sqrt2)^(x^3-3x^2+4)=t\) , \(t>0\) . Тогаш равенката ќе добие форма \
Постепено ќе ги запишуваме условите под кои првобитната равенка ќе има шест решенија.
забележи, тоа квадратна равенка\((*)\) може да има најмногу две решенија. Било кој кубна равенка\(Ax^3+Bx^2+Cx+D=0\) може да има не повеќе од три решенија. Според тоа, ако равенката \((*)\) има два различни решенија(позитивно!, бидејќи \(t\) мора да биде поголемо од нула) \(t_1\) и \(t_2\), тогаш со правење на обратна замена, добиваме: \[\лево[\почеток(собрано)\почеток(порамнето) &(\sqrt2)^(x^3-3x^2+4)=t_1\\ &(\sqrt2)^(x^3-3x^2 +4)=t_2\крај (порамнет)\крај (собрано)\десно.\]Бидејќи секој позитивен број може да се претстави како \(\sqrt2\) до одреден степен, на пример, \(t_1=(\sqrt2)^(\log_(\sqrt2) t_1)\), тогаш првата равенка од множеството ќе се препише во форма \
Како што веќе рековме, секоја кубна равенка нема повеќе од три решенија, затоа, секоја равенка во множеството нема да има повеќе од три решенија. Тоа значи дека целиот сет нема да има повеќе од шест решенија.
Ова значи дека за првобитната равенка да има шест решенија, квадратната равенка \((*)\) мора да има две различни решенија, а секоја добиена кубна равенка (од множеството) мора да има три различни решенија (и не едно решение на една равенка треба да се совпадне со која било - по одлука на втората!)
Очигледно, ако квадратната равенка \((*)\) има едно решение, тогаш нема да добиеме шест решенија за првобитната равенка.
Така, планот за решение станува јасен. Да ги запишеме условите кои мора да се исполнат точка по точка.
1) За равенката \((*)\) да има две различни решенија, нејзината дискриминаторна мора да биде позитивна: \
2) Исто така, неопходно е двата корени да бидат позитивни (бидејќи \(t>0\) ). Ако производот на два корени е позитивен, а нивниот збир е позитивен, тогаш самите корени ќе бидат позитивни. Затоа, ви треба: \[\почеток(случаи) 12-a>0\\-(a-10)>0\end (случаи)\quad\Leftrightarrow\quad a<10\]
Така, веќе си обезбедивме два различни позитивни корени \(t_1\) и \(t_2\) .
3)
Ајде да ја погледнеме оваа равенка \
За што \(t\) ќе има три различни решенија? Така, утврдивме дека двата корени на равенката \((*)\) мора да лежат во интервалот \((1;4)\) . Како да се напише оваа состојба? Така, треба да ги пресечеме вредностите на параметарот \(a\) пронајдени во 1, 2 и 3 точки и ќе го добиеме одговорот: \[\почеток(случаи) a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\\ a<10\\
4 Сокриј Прикажи Нека функцијата е дадена со формулата: y=2x^(2)-3. Со доделување на какви било вредности на независната променлива x, можете да ги пресметате, користејќи ја оваа формула, соодветните вредности на зависната променлива y. На пример, ако x=-0,5, тогаш, користејќи ја формулата, откриваме дека соодветната вредност на y е y=2 \cdot (-0,5)^(2)-3=-2,5. Земајќи ја секоја вредност земена од аргументот x во формулата y=2x^(2)-3, можете да пресметате само една вредност од функцијата што одговара на неа. Функцијата може да се претстави како табела: Користејќи ја оваа табела, можете да видите дека за вредноста на аргументот −1 ќе одговара вредноста на функцијата −3; а вредноста x=2 ќе одговара на y=0 итн. Исто така, важно е да се знае дека секоја вредност на аргументот во табелата одговара само на една вредност на функцијата. Повеќе функции може да се специфицираат со помош на графикони. Со помош на график се утврдува која вредност на функцијата е во корелација со одредена вредност x. Најчесто, ова ќе биде приближна вредност на функцијата. Функцијата е дури и функција, кога f(-x)=f(x) за кој било x од доменот на дефиниција. Таквата функција ќе биде симетрична во однос на оската Oy. Функцијата е непарна функција, кога f(-x)=-f(x) за кој било x од доменот на дефиниција. Таквата функција ќе биде симетрична во однос на потеклото O (0;0) . Функцијата е ниту, ниту чуднои се нарекува општа функција, кога нема симетрија околу оската или потеклото. Да ја испитаме следнава функција за паритет: f(x)=3x^(3)-7x^(7) D(f)=(-\infty ; +\infty) со симетричен домен на дефиниција во однос на потеклото. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x). Тоа значи дека функцијата f(x)=3x^(3)-7x^(7) е непарна. Функцијата y=f(x) , во чие подрачје важи еднаквоста f(x+T)=f(x-T)=f(x) за кој било x, се вика периодична функцијасо период T \neq 0 . Повторување на графикот на функцијата на која било отсечка од оската x која има должина Т. Интервалите каде што функцијата е позитивна, односно f(x) > 0, се отсечки од оската на апсцисата што одговараат на точките на функционалниот график што лежат над оската на апсцисата. f(x) > 0 вклучено (x_(1); x_(2)) \ чаша (x_(3); +\infty) Интервали каде функцијата е негативна, односно f(x)< 0
- отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс. f(x)< 0
на (-\infty; x_(1)) \ чаша (x_(2); x_(3)) Ограничен одоздолаВообичаено е да се повика функцијата y=f(x), x \in X кога има број A за кој важи неравенката f(x) \geq A за кој било x \во X . Пример за функција ограничена одоздола: y=\sqrt(1+x^(2)) бидејќи y=\sqrt(1+x^(2)) \geq 1 за кој било x . Ограничено одозгораФункцијата y=f(x), x \in X се повикува кога има број B за кој важи неравенството f(x) \neq B за било кој x \во X . Пример за функција ограничена подолу: y=\sqrt(1-x^(2)), x \in [-1;1]бидејќи y=\sqrt(1+x^(2)) \neq 1 за кој било x \in [-1;1] . ОграничениВообичаено е да се повика функцијата y=f(x), x \во X кога има број K > 0 за кој неравенството \left | f(x)\десно | \neq K за кој било x \во X. Пример за ограничена функција: y=\sin x е ограничен на целата бројна оска, бидејќи \лево | \sin x \десно | \нед 1. Вообичаено е да се зборува за функција која се зголемува на интервалот што се разгледува како зголемување на функцијататогаш, кога поголема вредност на x одговара на поголема вредност на функцијата y=f(x) . Следи дека земајќи две произволни вредности на аргументот x_(1) и x_(2) од интервалот што се разгледува, со x_(1) > x_(2) , резултатот ќе биде y(x_(1)) > y(x_(2)). Се повикува функцијата што се намалува на интервалот што се разгледува функцијата за намалувањекога поголема вредност на x одговара на помала вредност на функцијата y(x) . Следи дека, земајќи ги од разгледуваниот интервал две произволни вредности на аргументот x_(1) и x_(2) и x_(1) > x_(2), резултатот ќе биде y(x_(1))< y(x_{2})
. Корени на функцииВообичаено е да се нарекуваат точките во кои функцијата F=y(x) ја сече оската на апсцисата (тие се добиваат со решавање на равенката y(x)=0). а) Ако за x > 0 една парна функција се зголемува, тогаш таа се намалува за x< 0
б) Кога парна функција се намалува на x > 0, тогаш таа се зголемува на x< 0
в) Кога непарната функција се зголемува на x > 0, тогаш таа исто така се зголемува на x< 0
г) Кога непарната функција се намалува за x > 0, тогаш ќе се намали и за x< 0
Минимална точка на функцијата y=f(x) обично се нарекува точка x=x_(0) чие соседство ќе има други точки (освен точката x=x_(0)), а за нив неравенката f(x) > f тогаш ќе биде задоволен (x_(0)) . y_(min) - означување на функцијата во точката min. Максимална точка на функцијата y=f(x) обично се нарекува точка x=x_(0) чие соседство ќе има други точки (освен точката x=x_(0)), а за нив тогаш ќе се задоволи неравенката f(x)< f(x^{0})
. y_{max}
- обозначение функции в точке max.
Според теоремата на Ферма: f"(x)=0 кога функцијата f(x) која е диференцијабилна во точката x_(0) ќе има екстрем во оваа точка. Чекори за пресметка: Проверете дали графикот на функцијата е симетричен во однос на оската Y.Симетрија значи огледална слика на графикот во однос на оската на ординатите. Ако делот од графиконот десно од Y-оската (позитивни вредности на независната променлива) е ист како делот од графиконот лево од Y-оската (негативни вредности на независната променлива ), графикот е симетричен во однос на оската Y. Ако функцијата е симетрична во однос на y-оската, функцијата е парна. Проверете дали графикот на функцијата е симетричен во однос на потеклото.Потеклото е точката со координати (0,0). Симетријата за потеклото значи дека позитивна вредност y (\displaystyle y)(со позитивна вредност x (\displaystyle x)) одговара на негативна вредност y (\displaystyle y)(со негативна вредност x (\displaystyle x)), и обратно. Непарните функции имаат симетрија за потеклото. Проверете дали графикот на функцијата има некаква симетрија.Последниот тип на функција е функција чиј график нема симетрија, односно нема огледална слика и во однос на оската на ординатите и во однос на потеклото. На пример, со оглед на функцијата .
Да ја разгледаме функцијата \(f(x)=x^3-3x^2+4\) .
Може да се факторизира: \
Според тоа, неговите нули се: \(x=-1;2\) .
Ако го најдеме изводот \(f"(x)=3x^2-6x\) , тогаш добиваме две екстремни точки \(x_(max)=0, x_(min)=2\) .
Затоа, графиконот изгледа вака: 
Гледаме дека секоја хоризонтална линија \(y=k\) , каде што \(0
Така, ви треба: \[\почеток(случаи) 0<\log_{\sqrt2}t_1<4\\ 0<\log_{\sqrt2}t_2<4\end{cases}\qquad (**)\]
Исто така, веднаш да забележиме дека ако броевите \(t_1\) и \(t_2\) се различни, тогаш броевите \(\log_(\sqrt2)t_1\) и \(\log_(\sqrt2)t_2\) ќе бидат различни, што значи равенките \(x^3-3x^2+4=\log_(\sqrt2) t_1\)И \(x^3-3x^2+4=\log_(\sqrt2) t_2\)ќе има различни корени.
Системот \((**)\) може да се преработи на следниов начин: \[\почеток(случаи) 1
Ние нема да ги испишеме корените експлицитно.
Да ја разгледаме функцијата \(g(t)=t^2+(a-10)t+12-a\) . Нејзиниот график е парабола со гранки нагоре, која има две точки на пресек со оската x (оваа состојба ја запишавме во став 1)). Како треба да изгледа неговиот график така што точките на пресек со оската x се во интервалот \((1;4)\)? Значи: 
Прво, вредностите \(g(1)\) и \(g(4)\) на функцијата во точките \(1\) и \(4\) мора да бидат позитивни, и второ, темето на параболата \(t_0\ ) исто така мора да биде во интервалот \((1;4)\) . Затоа, можеме да го напишеме системот: \[\почеток(случаи) 1+a-10+12-a>0\\ 4^2+(a-10)\cdot 4+12-a>0\\ 1<\dfrac{-(a-10)}2<4\end{cases}\quad\Leftrightarrow\quad 4Методи за одредување функција
x −2
−1
0
1
2
3
y −4
−3
−2
−1
0
1
Парна и непарна функција
Периодична функција


Ограничена функција
Функција за зголемување и намалување

.png)

.png)
Екстреми на функцијата
Предуслов
Доволна состојба
Најголемата и најмалата вредност на функцијата на интервал
.
За да го направите ова, користете милиметарска хартија или графички калкулатор. Изберете кој било број на вредности на независни променливи x (\displaystyle x)и приклучете ги во функцијата за да ги пресметате вредностите на зависната променлива y (\displaystyle y). Нацртајте ги пронајдените координати на точките на координатната рамнина, а потоа поврзете ги овие точки за да изградите график на функцијата.