Николај купил општа тетратка од 96 листови. Математички олимпијади и задачи на Олимпијадата. Ви посакуваме успех

Секции: Математика

Почитуван учесник на Олимпијадата!

Училишната олимпијада по математика се одржува во едно коло.
Има 5 задачи со различно ниво на тежина.
Не ви се претставени посебни барања во врска со извршувањето на работата. Формата на презентација на решенија за проблемите, како и методи на решавање, може да биде која било. Ако имате индивидуални размислувања за одредена задача, но не можете да го завршите решението, не двоумете се да ги искажете сите ваши мисли. Дури и делумно решените проблеми ќе добијат соодветен број бодови.
Почнете да ги решавате проблемите кои мислите дека се полесни, а потоа преминете на останатите. На овој начин ќе заштедите работно време.

Ви посакуваме успех!

Училишна сцена Серуска Олимпијадаученици по математика

5-то одделение.

Вежба 1. Во изразот 1*2*3*4*5, заменете го „*“ со акциони знаци и поставете ги заградите вака. Да се ​​добие израз чија вредност е 100.

Задача 2. Потребно е да се дешифрира ознаката на аритметичка еднаквост во која броевите се заменуваат со букви, а различните броеви се заменуваат со различни букви, идентични - идентични.

ПЕТ - ТРИ = ДВАСе знае дека наместо писмо Атреба да го замените бројот 2.

Задача 3. Како можете да користите вага без тегови за да поделите 80 кг клинци на два дела - 15 кг и 65 кг?

Задача 4. Пресечете ја фигурата прикажана на сликата на два еднакви дела, така што секој дел има по една ѕвезда. Можете да сечете само по линиите на решетката.

Задача 5. Чаша и чинија заедно чинат 25 рубли, а 4 чаши и 3 чинии чинат 88 рубли. Најдете ја цената на чашата и цената на чинијата.

6-то одделение.

Вежба 1. Споредете ги дропките без да ги намалите на заеднички именител.

Задача 2. Потребно е да се дешифрира ознаката на аритметичка еднаквост во која броевите се заменуваат со букви, а различните броеви се заменуваат со различни букви, а идентичните се заменуваат со идентични. Се претпоставува дека првобитната еднаквост е вистинита и напишана според вообичаените аритметички правила.

РАБОТА
+ ВОЛЈА
СРЕЌА

Задача 3. ВО летен кампТројца пријатели дојдоа да се одморат: Миша, Володија и Петја. Познато е дека секој од нив има едно од следниве презимиња: Иванов, Семенов, Герасимов. Миша не е Герасимов. Таткото на Володија е инженер. Володија е во 6-то одделение. Герасимов учи во 5-то одделение. Таткото на Иванов е учител. Како се презива секој од тројцата пријатели?

Задача 4. Поделете ја фигурата по линиите на решетката на четири еднакви делови, така што секој дел содржи една точка.

Задача 5. Вилинското коњче кое скока спиеше половина од секој ден од црвеното лето, танцуваше третина од времето од секој ден и пееше шестина од времето. Таа одлучила остатокот од своето време да го посвети на подготовките за зимата. Колку часа дневно се подготвувал Dragonfly за зима?

7-мо одделение.

Вежба 1. Решете ја загатката ако знаете дека најголемата цифра во бројот СИЛНО е 5:

ОДЛУЧИ
АКО
СИЛНИ

Задача 2. Решете ја равенката│7 - x│ = 9,3

Задача 3. По седум перења, должината, ширината и дебелината на сапунот беа преполовени. Колку перења ќе издржи преостанатиот сапун?

Задача 4 . Поделете правоаголник од 4 × 9 ќелии по страните на ќелиите на два еднакви дела, така што потоа можете да направите квадрат од нив.

Задача 5. Дрвената коцка беше обоена бела од сите страни, а потоа исеана на 64 идентични коцки. Колку коцки биле обоени од три страни? На двете страни?
Од една страна? Колку коцки не се обоени?

8-мо одделение.

Вежба 1. Со кои две цифри завршува бројот 13?

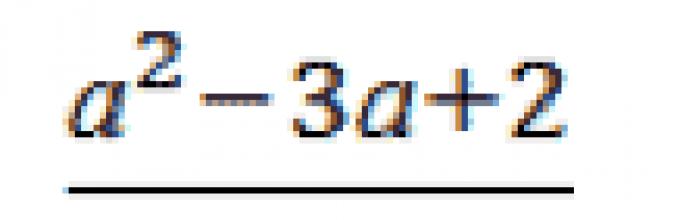
Задача 2. Намали ја фракцијата:

Задача 3. Училишниот драмски клуб се подготвува да постави извадок од бајката на А.С. Пушкин за цар Салтан, реши да ги распредели улогите меѓу учесниците.
„Јас ќе бидам Черномор“, рече Јура.
„Не, јас ќе бидам Черномор“, рече Коља.
„Во ред“, му призна Јура, „можам да го играм Гвидон“.
„Па, можам да станам Салтан“, Коља исто така покажа усогласеност.
- Се согласувам да бидам само Гидон! - рече Миша.
Желбите на момчињата беа исполнети. Како беа распределени улогите?

Задача 4. Во рамнокрак триаголник ABCсо основата AB = 8m е нацртана медијаната АД. Периметарот на триаголникот ACD е 2 m поголем од периметарот на триаголникот ABD. Најдете AC.

Задача 5. Николај купил општа тетратка од 96 листови и ги нумерирал страниците од 1 до 192. Внукот Артур искинал 35 листови од оваа тетратка и ги собрал сите 70 броеви напишани на нив. Можеше ли да успее во 2010 година?

9-то одделение.

Вежба 1. Најдете ја последната цифра од 1989 1989 година.

Задача 2. Збирот на корените на некои квадратна равенкае 1, а збирот на нивните квадрати е 2. Колку изнесува збирот на нивните коцки?

Задача 3. Користејќи три медијани m a, m b и m c ∆ ABC, пронајдете ја должината на страната AC = b.

Задача 4. Намалете ја фракцијата .

Задача 5. На колку начини можете да изберете самогласка и согласка во зборот „камзол“?

Одделение 10.

Вежба 1. Во моментов има монети од 1, 2, 5, 10 рубли. Наведете ги сите суми на пари што може да се платат и со парен и со непарен број на монети.

Задача 2. Докажете дека 5 + 5 2 + 5 3 + … + 5 2010 е делив со 6.

Задача 3. Во четириаголник А БЕ ЦЕ ДЕдијагоналите се сечат во точка М. Познато е дека AM = 1,
VM = 2, SM = 4. По кои вредности ДМчетириаголник А БЕ ЦЕ ДЕдали е тоа трапез?

Задача 4. Решете го системот на равенки

Задача 5. Триесет ученици - десетто и единаесетто одделение - се ракуваа. Се испостави дека секој десеттоодделенец се ракувал со осум единаесеттоодделенци, а секој единаесетти се ракувал со седум десетти. Колку десетоодделенци имаше, а колку единаесетти?

Задача 16:

Дали е можно да се разменат 25 рубли користејќи десет сметки во апоени од 1, 3 и 5 рубли? Решение:

Одговор: Не

Петја купи општа тетратка со волумен од 96 листови и ги нумерира сите нејзини страници со броеви од 1 до 192. Васија искина 25 листови од оваа тетратка и ги собра сите 50 броеви напишани на нив. Дали можеше да успее во 1990 година? Решение:

На секој лист, збирот на броевите на страниците е непарен, а збирот од 25 непарни броеви е непарен.

Производот на 22 цели броеви е 1. Докажете дека нивниот збир не е нула. Решение:

Меѓу овие бројки - парен број„минус еден“, а за да може збирот да биде еднаков на нула, мора да има точно 11 од нив.

Дали е можно да се состави магичен квадратод првите 36 прости броеви? Решение:

Меѓу овие броеви, еден (2) е парен, а останатите се непарни. Според тоа, во правата каде што има два, збирот на броевите е непарен, а во други е парен.

По ред се пишуваат броевите од 1 до 10. Дали е можно да се постават знаците „+“ и „-“ меѓу нив така што вредноста на добиениот израз да биде еднаква на нула?

Забелешка: Ве молиме имајте предвид дека негативни броевисе исто така парни и непарни. Решение:

Всушност, збирот на броевите од 1 до 10 е 55, а со менување на знаците во него, го менуваме целиот израз во парен број.

Скакулецот скока во права линија, а првиот пат скокна 1 см во некоја насока, вториот пат - 2 см итн. Докажете дека по скоковите во 1985 година не може да заврши таму каде што почнал. Решение:

Забелешка: Збирот 1 + 2 + … + 1985 е непарен.

На таблата се напишани броевите 1, 2, 3, ..., 1984, 1985. Дозволено е да избришете кои било два броја од таблата и наместо тоа да го запишете модулот на нивната разлика. На крајот ќе остане само еден број на таблата. Дали може да биде нула? Решение:

Проверете дали горенаведените операции не ја менуваат парноста на збирот на сите броеви запишани на таблата.

Дали е можно да се покрие шаховска табла со 1 × 2 домино така што само квадратите a1 и h8 да останат слободни? Решение:

Секое домино покрива еден црн и еден бел квадрат, а кога се отфрлаат квадратите a1 и h8, има 2 помалку црни квадрати од белите.

На 17-цифрениот број додадовме број напишан со исти цифри, но во обратен редослед. Докажете дека барем една цифра од добиениот збир е парна. Решение:

Размислете за два случаи: збирот на првата и последната цифра од некој број е помал од 10, а збирот на првата и последната цифра од некој број не е помал од 10. Ако претпоставиме дека сите цифри од збирот се непарни, тогаш во првиот случај не треба да има ниту едно пренесување во цифрите (што е очигледно, доведува до контрадикција), а во вториот случај, присуството на носење при движење од десно кон лево или лево кон десно се менува со отсуството на носење, и како резултат добиваме дека цифрата на збирот во деветтата цифра е нужно парна.

Во народниот одред има 100 луѓе, а секоја вечер по тројца одат на смена. Може ли после некое време да испадне дека сите биле дежурни со секого точно еднаш? Решение:

Бидејќи на секоја должност во која учествува оваа личност, тој е на должност со уште двајца, потоа сите други можат да се поделат во парови. Сепак, 99 е непарен број.

На правата има 45 точки кои лежат надвор од отсечката AB. Докажете дека збирот на растојанијата од овие точки до точката А не е еднаков на збирот на растојанијата од овие точки до точката Б. Решение:

За која било точка X што лежи надвор од AB, имаме AX - BX = ± AB. Ако претпоставиме дека збировите на растојанијата се еднакви, тогаш добиваме дека изразот ± AB ± AB ± … ± AB, кој вклучува 45 членови, е еднаков на нула. Но, ова е невозможно.

Има 9 броеви подредени во круг - 4 единици и 5 нули. Секоја секунда на броевите се врши следнава операција: меѓу соседните броеви ако се различни се става нула, а ако се еднакви единица; после тоа се бришат старите бројки. Дали после некое време сите бројки можат да станат исти? Решение:

Јасно е дека комбинација од девет не може да се добие пред девет нули. Ако имало девет нули, тогаш на претходниот потег нулите и единиците морале да се менуваат наизменично, што е невозможно, бидејќи има само непарен број од нив.

На тркалезна маса седат 25 момчиња и 25 девојчиња. Докажете дека некои од луѓето што седат на маса ги имаат и двете момчиња за соседи. Решение:

Ајде да го спроведеме нашиот доказ со контрадикторност. Ајде да ги нумерираме по ред сите седнати на масата, почнувајќи од некое место. Доколку е вклучено кто местоседи момче, тогаш јасно е дека девојчињата седат на (k - 2) и (k + 2) место. Но, бидејќи има еднаков број на момчиња и девојчиња, тогаш за секоја девојка што седи на n-то место, точно е дека има момчиња кои седат на (n - 2) и (n + 2) место. Ако сега ги земеме предвид само оние 25 луѓе кои седат на „рамномерни“ седишта, ќе откриеме дека меѓу нив момчињата и девојчињата се менуваат ако одиме околу масата во некоја насока. Но, 25 е непарен број.

Полжавот ползи по авионот со постојана брзина, вртејќи се под прав агол на секои 15 минути. Докажете дека таа може да се врати на почетната точка само по цел број часови. Решение:

Јасно е дека бројот a на области во кои полжавот ползел нагоре или надолу е еднаков на бројот на области во кои ползел десно или лево. Останува само да се забележи дека a е рамномерно.

Три скакулци играат прескокнување на права линија. Секој пат кога еден од нив прескокнува над другиот (но не и двете одеднаш!). Дали можат да завршат на истите места по скокот во 1991 година? Решение:

Да ги означиме скакулците A, B и C. Да го наречеме распоредот на скакулците ABC, BCA и CAB (од лево кон десно) точен, а ACB, BAC и CBA неточен. Лесно е да се види дека со секој скок се менува типот на уредување.

Има 101 монета, од кои 50 се лажни, а по тежина се разликуваат за 1 грам од вистинските. Петја зеде една паричка и во една вага со стрелка што ја покажува разликата во тежините на чашите, сака да утврди дали е фалсификувана. Дали ќе може да го направи тоа? Решение:

Треба да ја оставите оваа паричка настрана, а потоа да ги поделите преостанатите 100 монети на два купа од по 50 монети и да ги споредите тежините на овие купови. Ако се разликуваат за парен број грами, тогаш паричката што нè интересира е реална. Ако разликата во тежините е непарна, тогаш монетата е фалсификувана.

Дали е можно еднаш по ред да се запишуваат броевите од 1 до 9 за да има непарен број цифри помеѓу една и две, два и три, ..., осум и девет? Решение:

Во спротивно, сите броеви по ред би биле на места со ист паритет.

Ова дело Петја купи општа тетратка со волумен од 96 листови и ги нумерираше сите негови страници по редослед со броеви од 1 до 192. Васија го искина (Тест) на темата (ACD и финансиска анализа), беше завршена по индивидуална нарачка од страна на специјалисти на нашата компанија и го помина својот успешна одбрана. Работа - Петја купи општа тетратка со волумен од 96 листови и ги нумерира сите нејзини страници по редослед со броеви од 1 до 192. Васија ја искина ACD на темата и финансиската анализа ја одразува нејзината тема и логичната компонента на нејзиното откривање, се открива суштината на прашањето што се проучува, на оваа тема се истакнуваат главните одредби и водечките идеи.
Работа - Петја купи општа тетратка со волумен од 96 листови и ги нумерира сите нејзини страници по редослед со броеви од 1 до 192. Васија ја искина, содржи: табели, цртежи, најнови литературни извори, годината кога е поднесено делото и одбранета - 2017 година. Во делото, Петја купи општ тетратка од 96 листови и ги нумерираше сите негови страници по редослед со броеви од 1 до 192. Васија извлечена (АХД и финансиска анализа) ја открива релевантноста на темата за истражување, ја одразува степен на развиеност на проблемот, врз основа на длабока проценка и анализа на научни и методолошка литература, во работата на темата ACD и финансиска анализа сеопфатно се разгледуваат предметот на анализа и неговите прашања, како од теоретска така и од практична страна, се формулираат целта и конкретните цели на темата што се разгледува, постои логика на презентација на материјалот и неговиот редослед.