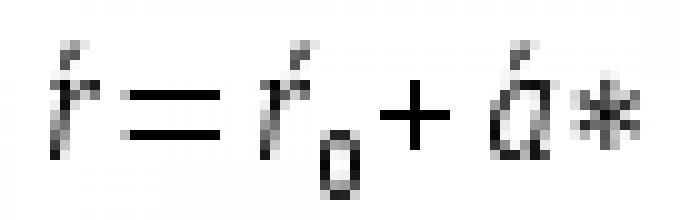– општа равенка на рамнина во вселената
Нормален вектор на рамнина
Нормален вектор на рамнина е ненулта вектор ортогонален на секој вектор што лежи во рамнината.
Равенка на рамнина што минува низ точка со даден нормален вектор
– равенка на рамнината што минува низ точката M0 со даден нормален вектор
Вектори за насока на рамнината
Два неколинеарни вектори паралелни на рамнината ги нарекуваме вектори на насоката на рамнината
Равенки на параметриска рамнина
![]() – параметарска равенка на рамнината во векторска форма
– параметарска равенка на рамнината во векторска форма
 – параметарска равенка на рамнината во координати
– параметарска равенка на рамнината во координати
Равенка на рамнина низ дадена точка и два вектори на насока
– фиксна точка
-Само точка lol
-компланарни, што значи дека нивниот мешан производ е 0.

Равенка на рамнина што минува низ три дадени точки
 – равенка на рамнина низ три точки
– равенка на рамнина низ три точки
Равенка на рамнина во отсечки
– равенка на рамнината во отсечки
Доказ
За да го докажеме ова, го користиме фактот дека нашата рамнина минува низ A,B,C и нормалниот вектор

Да ги замениме координатите на точката и векторот n во равенката на рамнината со нормален вектор
Ајде да поделиме сè по и да добиеме
Така оди.
Равенка на нормална рамнина
– аголот помеѓу волот и нормалниот вектор до рамнината што произлегува од О.
– аголот помеѓу oy и нормалниот вектор до рамнината што произлегува од О.
– аголот помеѓу oz и нормалниот вектор до рамнината што произлегува од О.
– растојание од потеклото до авионот.
Доказ или некои такви глупости
![]()
Знакот е спротивен на Д.
Исто и за останатите косинуси. Крај.
Растојание од точка до авион
Точка S, рамнина
– ориентирано растојание од точката S до рамнината
Ако , тогаш S и O лежат на спротивните страни на рамнината
Ако , тогаш S и O лежат на иста страна
Помножете се со n 
![]()
Релативната положба на две линии во просторот
Агол помеѓу рамнините
Кога се вкрстуваат, се формираат два пара вертикални диедрални агли, најмалиот се нарекува агол помеѓу рамнините
Права линија во просторот
Права линија во просторот може да се определи како
Пресек на две рамнини:
![]()
![]()
Параметриски равенки на права
– параметарска равенка на права линија во векторска форма
– параметарска равенка на права линија во координати
Канонска равенка
![]() – канонска равенка на права линија.
– канонска равенка на права линија.
Равенка на права што минува низ две дадени точки
![]()
![]() – канонска равенка на права линија во векторска форма;
– канонска равенка на права линија во векторска форма;
Релативната положба на две линии во просторот
Релативната положба на права линија и рамнина во вселената
Агол помеѓу права линија и рамнина
Растојание од точка до линија во просторот
a е векторот на насоката на нашата права линија.
– произволна точка што припаѓа на дадена права
– точката до која ја бараме далечината.
Растојание помеѓу две линии на вкрстување
Растојание помеѓу две паралелни прави
М1 – точка која припаѓа на првата линија
М2 – точка која припаѓа на втората линија
![]()
Криви и површини од втор ред
Елипса е збир на точки на рамнина, збирот на растојанијата од кои до две дадени точки (фокуси) е константна вредност.
Канонска равенка на елипса



Замени со
![]()
Поделете по
Својства на елипсата
Пресек со координатни оски
Потекло
Релативна симетрија
Елипсата е крива што лежи во ограничен дел од авионот
Елипса може да се добие од круг со истегнување или компресирање
Параметриска равенка на елипса:
– директорки
Хипербола
Хипербола е збир на точки на рамнина за кои модулот на разликата во растојанија до 2 дадени точки (фокуси) е константна вредност (2а)

Го правиме истото како и со елипсата, добиваме
Замени со
Поделете по
Својства на хипербола
;
![]()
– директорки
Асимптота
Асимптота е права линија до која кривата се приближува без ограничување, оддалечувајќи се до бесконечноста.
Парабола

Својства на параворката
Врска помеѓу елипса, хипербола и парабола.
Врската помеѓу овие криви има алгебарско објаснување: сите тие се дадени со равенки од втор степен. Во секој координатен систем, равенките на овие криви имаат форма: ax 2 +bxy+cy 2 +dx+ey+f=0, каде што a, b, c, d, e, f се броеви
Конвертирање на правоаголни Декартови координатни системи
Пренос на паралелен координатен систем
![]()
– O’ во стариот координатен систем
– координати на точката во стариот координатен систем
– координати на точката во новиот координатен систем
Координати на точката во новиот координатен систем.
Ротација во правоаголен Декартов координатен систем
– нов координатен систем
![]()
Преодна матрица од старата основа кон новата
![]() – (под првата колона Јас’
, под вториот - ј’
) преодна матрица од основата Јас,јдо основата Јас’
,ј’
– (под првата колона Јас’
, под вториот - ј’
) преодна матрица од основата Јас,јдо основата Јас’
,ј’
![]()
![]()
Општ случај
Ротирање на координатен систем
Ротирање на координатен систем
Превод на паралелно потекло
1 опција
Опција 2
Општа равенка на линии од втор ред и нејзино редуцирање во канонска форма
– општа форма на равенки за криви од втор ред
Класификација на криви од втор ред
Елипсоид
![]()
Елипсоидни делови
– елипса
– елипса
![]()
![]()
Елипсоиди на револуцијата
Елипсоидите на револуцијата се или заоблени или испакнати сфероиди, во зависност од тоа околу што ротираме.
Хиперболоид со една лента
![]()

Пресеци на хиперболоид со една лента
– хипербола со реална оска
– хипербола со реална оска x
![]()
Резултатот е елипса за кој било ч. Така оди.
Хиперболоиди на револуција со една лента
Еднолист хиперболоид на револуција може да се добие со ротирање на хиперболата околу нејзината имагинарна оска.
Хиперболоид со два листа
![]()
Пресеци на хиперболоид со два листа 
- хипербола со дејство. axisoz
– хипербола со реална оска
![]()
Конус 
![]()
– пар линии кои се вкрстуваат
– пар линии кои се вкрстуваат
Елипсовиден параболоид 
![]() - парабола
- парабола
– парабола
Ротации
Ако , тогаш елипсовиден параболоид е површина на револуција формирана со ротација на парабола околу својата оска на симетрија.
Хиперболичен параболоид

Парабола
– парабола
h>0 хипербола со реална оска паралелна на x
ч<0 гипербола с действительной осью паралльной оу и мнимой ох
Под цилиндар ја подразбираме површината што ќе се добие кога права линија се движи во просторот, без промена на нејзиниот правец; ако правата се движи во однос на oz, тогаш равенката на цилиндерот е равенката на пресекот со рамнината xoy.
Елипсовиден цилиндар

Хиперболичен цилиндар

Параболичен цилиндар

Праволиниски генератори на површини од втор ред
Правите линии кои целосно лежат на површината се нарекуваат праволиниски генератори на површината.
![]()
![]()


Површини на револуција
Ебати ти цицач
Приказ
Приказда го наречеме правилото според кое секој елемент од множеството А се поврзува со еден или повеќе елементи од множеството Б. Ако на секој му е доделен по еден елемент од множеството Б, тогаш се повикува пресликувањето недвосмислена, во спротивно двосмислена.
Трансформацијана множество е мапирање еден-на-еден на множество врз себе
Инјекција
Инјектирање или мапирање еден-на-еден од множеството А до множеството Б
(различни елементи на а одговараат на различни елементи од Б) на пример y=x^2

Сурјекција
Свртување или пресликување на множеството А во множеството Б
За секое Б има најмалку едно А (на пример синус)

Секој елемент од множеството Б одговара само на еден елемент од множеството А. (на пример y=x)
Досега ја разгледувавме равенката на површина во просторот со координатни оски X, Y, Z во експлицитна форма или во имплицитна форма
![]()
Можете да ги напишете равенките на површината во параметарска форма, изразувајќи ги координатите на нејзините точки како функции на два независни параметри на променливи и
Ќе претпоставиме дека овие функции се едновредни, континуирани и имаат континуирани изводи до втор ред во одреден опсег на параметри
Ако ги замениме овие координатни изрази преку u и v во левата страна на равенката (37), тогаш треба да добиеме идентитет во однос на u и V. Диференцирајќи го овој идентитет во однос на независните променливи u и v, ќе имаме

Сметајќи ги овие равенки како две хомогени равенки во однос и применувајќи ја алгебарската лема спомената во , добиваме

каде k е одреден коефициент на пропорционалност.
Сметаме дека факторот k и барем една од разликите на десната страна на последните формули не се нула.
За краткост, да ги означиме напишаните три разлики на следниов начин:

Како што е познато, равенката на тангентата рамнина на нашата површина во одредена точка (x, y, z) може да се запише во форма
или, заменувајќи ги пропорционалните величини, можеме да ја преработиме равенката на тангентата рамнина на следниов начин:
Познато е дека коефициентите во оваа равенка се пропорционални на косинусите на насоката на нормалата кон површината.
Позицијата на променливата точка М на површината се карактеризира со вредностите на параметрите u и v, а овие параметри обично се нарекуваат координати на површинските точки или координатни параметри.
Давајќи ги параметрите u и v константни вредности, добиваме две фамилии на прави на површината, кои ќе ги наречеме координатни линии на површината: координатни линии по кои се менува само v и координатни линии по кои се менува само u. Овие две фамилии на координатни линии обезбедуваат координатна мрежа на површината.
Како пример, земете ја сферата со центар на почеток и радиус R. Параметарските равенки на таквата сфера може да се напишат како
Координативните линии претставуваат во овој случај, очигледно, паралели и меридијани на нашата сфера.
Апстрахирајќи од координатните оски, можеме да ја карактеризираме површината со вектор со променлив радиус што оди од константната точка O до променливата точка M на нашата површина. Делумните деривати на овој вектор на радиус во однос на параметрите очигледно ќе дадат вектори насочени по тангентите на координатните линии. Компоненти на овие вектори долж оските
ќе, соодветно, и од ова е јасно дека коефициентите во равенката на тангентата рамнина (39) се компоненти на векторскиот производ Овој векторски производ е вектор нормален на тангентите, т.е. вектор насочен по должината на нормалата на површината. Квадратот на должината на овој вектор се изразува, очигледно, со скаларниот производ на векторот и самиот тој, т.е., едноставно кажано, квадратот на овој вектор 1). Во продолжение, единечниот вектор нормален на површината ќе игра значајна улога, која очигледно можеме да ја напишеме во форма

Со менување на редоследот на факторите во напишаниот векторски производ, добиваме спротивна насока за векторот (40). Во продолжение ќе го поправиме редоследот на факторите на одреден начин, односно на одреден начин ќе го поправиме правецот на нормалата кон површината.
Да земеме одредена точка М на површината и да нацртаме низ оваа точка крива (L) што лежи на површината. Оваа крива, општо земено, не е координатна линија, и Well и v ќе се менуваат по неа. Насоката на тангентата на оваа крива ќе се определи со векторот ако претпоставиме дека долж (L) во соседството на точката параметарот v е функција да има извод. Од ова е јасно дека насоката на тангентата на кривата нацртана на површината во која било точка М од оваа крива е целосно карактеризирана со вредноста во оваа точка. При дефинирање на рамнината на тангентната рамнина и изведување на нејзината равенка (39), претпоставивме дека функциите (38) во разгледуваната точка и нејзината близина имаат континуирани парцијални изводи и дека барем еден од коефициентите на равенката (39) е ненула во точката е предмет на разгледување.
Секоја равенка од прв степен во однос на координатите x, y, z
Ax + By + Cz +D = 0 (3,1)
дефинира рамнина и обратно: која било рамнина може да се претстави со равенката (3.1), која се нарекува равенка на рамнина.
Вектор n(A, B, C) се нарекува ортогонална на рамнината нормален векторрамнина. Во равенката (3.1), коефициентите A, B, C истовремено не се еднакви на 0.
Посебни случаи на равенката (3.1):
1. D = 0, Ax+By+Cz = 0 - рамнината минува низ потеклото.
2. C = 0, Ax+By+D = 0 - рамнината е паралелна со оската Оз.
3. C = D = 0, Ax + By = 0 - рамнината минува низ оската Оз.
4. B = C = 0, Ax + D = 0 - рамнината е паралелна со рамнината Oyz.
Равенки на координатни рамнини: x = 0, y = 0, z = 0.
Права линија во просторот може да се одреди:
1) како линија на пресек на две рамнини, т.е. систем на равенки:
A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)
2) според нејзините две точки M 1 (x 1, y 1, z 1) и M 2 (x 2, y 2, z 2), тогаш правата линија што минува низ нив е дадена со равенките:
3) точката M 1 (x 1, y 1, z 1) што и припаѓа и векторот а(m, n, p), колинеарно на него. Тогаш правата линија се одредува со равенките:
Се повикуваат равенките (3.4). канонски равенки на правата.
Вектор аповикани правец вектор директно.
Параметриски равенки на правадобиваме со изедначување на секоја од односите (3.4) со параметарот t:
x = x 1 + mt, y = y 1 + nt, z = z 1 + p t. (3.5)
Решавање на системот (3.2) како систем на линеарни равенки за непознати xИ y, доаѓаме до равенките на правата во проекцииили да дадени равенки на права линија :
x = mz + a, y = nz + b. (3.6)
Од равенките (3.6) можеме да одиме до канонските равенки, наоѓајќи zод секоја равенка и изедначување на добиените вредности:
Од општите равенки (3.2) можете да отидете до канонските на друг начин, ако најдете некоја точка на оваа права и нејзиниот вектор на насока n= [n 1 , n 2 ], каде n 1 (A 1, B 1, C 1) и n 2 (A 2 , B 2 , C 2 ) - нормални вектори на дадени рамнини. Ако еден од именителот m, nили Рво равенките (3.4) излегува дека е еднаков на нула, тогаш броителот на соодветната дропка мора да се постави еднаков на нула, т.е. систем
е еквивалентно на системот; таквата права линија е нормална на оската Ox.
Системот е еквивалентен на системот x = x 1, y = y 1; правата линија е паралелна со оската Оз.
Пример 1.15. Напишете равенка за рамнината, знаејќи дека точката A(1,-1,3) служи како основа на нормална извлечена од почетокот на оваа рамнина.
Решение.Според проблемските услови векторот ОП(1,-1,3) е нормален вектор на рамнината, тогаш неговата равенка може да се запише како
x-y+3z+D=0. Заменувајќи ги координатите на точката A(1,-1,3) што припаѓа на рамнината, наоѓаме D: 1-(-1)+3 × 3+D = 0 Þ D = -11. Значи x-y+3z-11=0.
Пример 1.16. Напишете равенка за рамнина што минува низ оската Oz и формира агол од 60° со рамнината 2x+y-z-7=0.
Решение.Рамнината што минува низ оската Оз е дадена со равенката Ax+By=0, каде што A и B не исчезнуваат истовремено. Нека не Б
е еднакво на 0, A/Bx+y=0. Користење на косинусната формула за аголот помеѓу две рамнини
Решавајќи ја квадратната равенка 3m 2 + 8m - 3 = 0, ги наоѓаме нејзините корени
m 1 = 1/3, m 2 = -3, од каде што добиваме две рамнини 1/3x+y = 0 и -3x+y = 0.
Пример 1.17.Составете ги канонските равенки на правата:
5x + y + z = 0, 2x + 3y - 2z + 5 = 0.
Решение.Канонските равенки на правата имаат форма:
Каде m, n, стр- координати на векторот за насочување на права линија, x 1, y 1, z 1- координати на која било точка што припаѓа на права. Правата линија се дефинира како линија на пресек на две рамнини. За да се најде точка што припаѓа на права, една од координатите е фиксирана (најлесно е да се постави, на пример, x=0) и добиениот систем се решава како систем од линеарни равенки со две непознати. Значи, нека x=0, тогаш y + z = 0, 3y - 2z+ 5 = 0, па оттука y=-1, z=1. Ги најдовме координатите на точката M(x 1, y 1, z 1) кои припаѓаат на оваа права: M (0,-1,1). Векторот на насоката на права линија е лесно да се најде, знаејќи ги нормалните вектори на оригиналните рамнини n 1 (5,1,1) и n 2 (2,3,-2). Потоа
Канонските равенки на правата имаат форма: x/(-5) = (y + 1)/12 =
= (z - 1)/13.
Векторски и параметарски равенки на рамнината.Нека r 0 и r се вектори на радиусот на точките M 0 и M, соодветно. Тогаш M 0 M = r - r 0, и услов (5.1) дека точката M припаѓа на рамнина што поминува низ точката M 0 нормално вектор без нула n (сл. 5.2, а), може да се напише со користење производ со точкикако сооднос
n(r - r 0) = 0, (5.4)
кој се нарекува векторска равенка на рамнината.
Фиксна рамнина во просторот одговара на множество вектори паралелни на него, т.е. простор V 2. Ајде да избереме во овој простор основа e 1, e 2, т.е. пар неколинеарни вектори паралелни на разгледуваната рамнина и точка M 0 на рамнината. Ако точката M припаѓа на рамнината, тогаш ова е еквивалентно на фактот дека векторот M 0 M е паралелен со него (слика 5.2, б), т.е. припаѓа на посочениот простор V 2 . Ова значи дека постои проширување на векторот M 0 M во основата e 1, e 2, т.е. има броеви t 1 и t 2 за кои M 0 M = t 1 e 1 + t 2 e 2. Откако ја напишавме левата страна на оваа равенка преку векторите на радиус r 0 и r на точките M 0 и M, соодветно, добиваме равенка на векторска параметарска рамнина
r = r 0 + t 1 e 1 + t 2 e 2 , t 1 , t 1 ∈ R. (5.5)
Да се премине од еднаквоста на векторите во (5.5) на нивната еднаквост координати, означете со (x 0 ; y 0 ; z 0), (x; y; z) координати на точки M 0, M и преку (e 1x; e 1y; e 1z), (e 2x; e 2y; e 2z) координатите на векторите e 1, e 2. Изедначувајќи ги координатите на векторите r и r 0 + t 1 e 1 + t 2 e 2 со истото име, добиваме равенки на параметарски рамнини

Авион кој минува низ три точки.Да претпоставиме дека три точки M 1, M 2 и M 3 не лежат на иста права. Потоа, постои единствена рамнина π на која припаѓаат овие точки. Да ја најдеме равенката на оваа рамнина со формулирање на критериум за произволна точка М да припаѓа на дадена рамнина π. Потоа го запишуваме овој критериум преку координатите на точките. Наведениот критериум е опис на рамнината π како множество од оние точки M за кои векторите M 1 M 2, M 1 M 3 и M 1 M компланарни. Критериум за компланарност на три вектори е нивната еднаквост на нула мешан производ(види 3.2). Мешаниот производ се пресметува со користење одредница од трет ред, чии редови се координатите на векторите во ортонормална основа. Според тоа, ако (x i; yx i; Zx i) се координатите на точките Mx i, i = 1, 2, 3 и (x; y; z) се координати на точката M, тогаш M 1 M = (x-x 1; y-y 1; z-z 1), M 1 M 2 = (x 2 -x 1; y 2 -y 1; z 2 -z 1), M 1 M 3 = (x 3 -x 1; y 3 -y 1 ; z 3 -z 1 ) и условот мешаниот производ на овие вектори да биде еднаков на нула има форма
Откако ја пресметавме детерминантата, добиваме линеарнаво однос на x, y, z равенката, што е општа равенка на саканата рамнина. На пример, ако прошири ја детерминантата по првата линија, тогаш добиваме
Оваа еднаквост, по пресметувањето на детерминантите и отворањето на заградите, се претвора во општата равенка на рамнината.
Забележете дека коефициентите на променливите во последната равенка се совпаѓаат со координатите векторски производ M 1 M 2 × M 1 M 3 . Овој векторски производ, бидејќи е производ на два неколинеарни вектори паралелни на рамнината π, дава ненула вектор нормален на π, т.е. неа нормален вектор. Значи, изгледот на координатите на векторскиот производ како коефициенти на општата равенка на рамнината е сосема природна.
Разгледајте го следниот посебен случај на рамнина што минува низ три точки. Точките M 1 (a; 0; 0), M 2 (0; b; 0), M 3 (0; 0; c), abc ≠ 0, не лежат на иста права линија и дефинираат рамнина што отсекува отсечки на координатните оски не-нулта должина (сл. 5.3). Овде, „должини на сегменти“ се подразбира вредноста на ненулта координати на векторите на радиусот на точките M i, i = 1,2,3.

Бидејќи M 1 M 2 = (-a; b; 0), M 1 M 3 = (-a; 0; c), M 1 M = (x-a; y; z), тогаш равенката (5.7) ја зема формата

Откако ја пресметавме детерминантата, наоѓаме bc(x - a) + acy + abz = 0, ја делиме добиената равенка со abc и го поместуваме слободниот член на десната страна,
x/a + y/b + z/c = 1.
Оваа равенка се нарекува равенка на рамнината во отсечки.
Пример 5.2.Да ја најдеме општата равенка на рамнина која минува низ точка со координати (1; 1; 2) и отсекува отсечки со еднаква должина од координатните оски.
Равенката на рамнината во отсечки, под услов да отсекува отсечки со еднаква должина од координатните оски, да речеме a ≠ 0, има форма x/a + y/b + z/c = 1. Оваа равенка мора да биде исполнета со координатите (1; 1; 2) позната точка на рамнината, т.е. важи равенството 4/a = 1. Според тоа, a = 4 и бараната равенка е x + y + z - 4 = 0.
Равенка на нормална рамнина.Да разгледаме некоја рамнина π во вселената. Ние го поправаме за неа единицанормално вектор n, насочено од потекло„кон рамнината“, и со p означете го растојанието од потеклото O на координатниот систем до рамнината π (сл. 5.4). Ако рамнината минува низ потеклото на координатниот систем, тогаш p = 0, и која било од двете можни насоки може да се избере како насока за нормалниот вектор n.
Ако точката М припаѓа на рамнината π, тогаш тоа е еквивалентно на фактот дека правописна векторска проекцијаОМ кон насокатавекторот n е еднаков на p, т.е. условот nOM = pr n OM = p е задоволен, бидејќи должина на векторот n е еднакво на еден.
Да ги означиме координатите на точката M со (x; y; z) и нека n = (cosα; cosβ; cosγ) (да потсетиме дека за единечен вектор n неговиот насока косинуси cosα, cosβ, cosγ се и неговите координати). Запишувајќи го скаларниот производ во еднаквост nOM = p во координатна форма, добиваме равенка на нормална рамнина
xcosα + ycosbeta; + zcosγ - p = 0.

Слично на случајот со права на рамнина, општата равенка на рамнината во вселената може да се трансформира во нејзината нормална равенка со делење со фактор за нормализирање.
За рамнината равенка Ax + By + Cz + D = 0, нормализирачкиот фактор е бројот ±√(A 2 + B 2 + C 2), чиј знак е избран спроти знакот D. Во апсолутна вредност, нормализирачкиот фактор е должината на нормалниот вектор (A; B; C) рамнина, а знакот одговара на саканата насока на единечниот нормален вектор на рамнината. Ако рамнината минува низ потеклото на координатниот систем, т.е. D = 0, тогаш знакот на нормализирачкиот фактор може да се избере на кој било начин.
Една од потточките на темата „Равенка на права на рамнина“ е прашањето за изготвување параметарски равенки на права на рамнина во правоаголен координатен систем. Написот подолу го разгледува принципот на составување на такви равенки со оглед на одредени познати податоци. Ќе покажеме како да преминеме од параметарски равенки до равенки од различен тип; Ајде да погледнеме во решавање на типични проблеми.
Специфична линија може да се дефинира со одредување на точка што припаѓа на оваа права и вектор на насока на правата.
Да речеме дека ни е даден правоаголен координатен систем O x y. И, исто така, дадена е права линија a, што ја означува точката M 1 што лежи на неа (x 1, y 1) и векторот на насоката на дадената права линија a → = (a x, a y) . Да дадеме опис на дадената права а користејќи равенки.
Користиме произволна точка M (x, y) и добиваме вектор M 1 M → ; Да ги пресметаме неговите координати од координатите на почетната и крајната точка: M 1 M → = (x - x 1, y - y 1). Ајде да опишеме што добивме: права линија е дефинирана со множество точки M (x, y), поминува низ точката M 1 (x 1, y 1) и има вектор на насока a → = (a x, a y) . Ова множество дефинира права линија само кога векторите M 1 M → = (x - x 1, y - y 1) и a → = (a x, a y) се колинеарни.
Постои неопходен и доволен услов за колинеарност на вектори, кој во овој случај за векторите M 1 M → = (x - x 1, y - y 1) и a → = (a x, a y) може да се запише како равенка:
M 1 M → = λ · a → , каде што λ е некој реален број.
Дефиниција 1
Равенката M 1 M → = λ · a → се нарекува векторско-параметриска равенка на правата.
Во координатна форма изгледа вака:
M 1 M → = λ a → ⇔ x - x 1 = λ a x y - y 1 = λ a y ⇔ x = x 1 + a x λ y = y 1 + a y λ
Равенките на добиениот систем x = x 1 + a x · λ y = y 1 + a y · λ се нарекуваат параметарски равенки на права линија на рамнина во правоаголен координатен систем. Суштината на името е како што следува: координатите на сите точки на права линија може да се одредат со параметарски равенки на рамнина од формата x = x 1 + a x · λ y = y 1 + a y · λ со набројување на сите реални вредности на параметарот λ
Според горенаведеното, параметарските равенки на права линија на рамнината x = x 1 + a x · λ y = y 1 + a y · λ дефинираат права линија, која е наведена во правоаголен координатен систем, поминува низ точката М 1 (x 1, y 1) и има водич вектор a → = (a x, a y) . Следствено, ако се дадени координатите на одредена точка на права и координатите на нејзиниот вектор на насока, тогаш е можно веднаш да се запишат параметарските равенки на дадена права.
Пример 1
Потребно е да се состават параметарски равенки на права линија на рамнина во правоаголен координатен систем ако се дадени точката M 1 (2, 3) што му припаѓа и неговиот векторот на насоката. a → = (3 , 1) .
Решение
Врз основа на првичните податоци, добиваме: x 1 = 2, y 1 = 3, a x = 3, a y = 1. Параметарските равенки ќе изгледаат вака:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ
Дозволете ни јасно да илустрираме:

Одговор: x = 2 + 3 λ y = 3 + λ
Треба да се забележи: ако векторот a → = (a x , a y) служи како вектор на насока на правата a, а точките M 1 (x 1, y 1) и M 2 (x 2, y 2) припаѓаат на оваа права, а потоа може да се одреди со наведување параметарски равенки од формата: x = x 1 + a x · λ y = y 1 + a y · λ , како и оваа опција: x = x 2 + a x · λ y = y 2 + a y · λ .
На пример, даден ни е насочен вектор на права линија a → = (2, - 1), како и точките M 1 (1, - 2) и M 2 (3, - 3) кои припаѓаат на оваа линија. Тогаш правата линија се одредува со параметарските равенки: x = 1 + 2 · λ y = - 2 - λ или x = 3 + 2 · λ y = - 3 - λ.
Треба да обрнете внимание и на следниот факт: ако a → = (a x, a y) е векторот на насоката на правата a, тогаш кој било од векторите ќе биде неговиот вектор на насока μ · a → = (μ · a x, μ · a y) , каде што μ ϵ R , μ ≠ 0 .
Така, правата линија a на рамнина во правоаголен координатен систем може да се определи со параметарски равенки: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ за која било вредност на μ различна од нула.
Да речеме правата а е дадена со параметарските равенки x = 3 + 2 · λ y = - 2 - 5 · λ. Потоа a → = (2 , - 5) - векторот на насоката на оваа права линија. И, исто така, кој било од векторите μ · a → = (μ · 2, μ · - 5) = 2 μ, - 5 μ, μ ∈ R, μ ≠ 0 ќе стане водечки вектор за дадена права линија. За јасност, разгледајте специфичен вектор - 2 · a → = (- 4, 10), тој одговара на вредноста μ = - 2. Во овој случај, дадената права линија може да се определи и со параметарските равенки x = 3 - 4 · λ y = - 2 + 10 · λ.
Премин од параметарски равенки на права на рамнина во други равенки на дадена права и назад
При решавање на некои проблеми, употребата на параметарски равенки не е најоптималната опција, тогаш има потреба да се преведат параметарските равенки на права линија во равенки од права линија од различен тип. Ајде да погледнеме како да го направите ова.
Параметриските равенки на права линија од формата x = x 1 + a x · λ y = y 1 + a y · λ ќе одговараат на канонската равенка на права линија на рамнината x - x 1 a x = y - y 1 a y .
Да ја решиме секоја од параметарските равенки во однос на параметарот λ, да ги изедначиме десните страни на добиените еднаквости и да ја добиеме канонската равенка на дадената права линија:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y
Во овој случај, не треба да биде збунувачки ако x или a y се еднакви на нула.
Пример 2
Потребно е да се направи премин од параметарските равенки на правата линија x = 3 y = - 2 - 4 · λ до канонската равенка.
Решение
Дадените параметарски равенки да ги запишеме во следната форма: x = 3 + 0 · λ y = - 2 - 4 · λ
Да го изразиме параметарот λ во секоја од равенките: x = 3 + 0 λ y = - 2 - 4 λ ⇔ λ = x - 3 0 λ = y + 2 - 4
Да ги изедначиме десните страни на системот на равенки и да ја добиеме потребната канонска равенка на права линија на рамнината:
x - 3 0 = y + 2 - 4
Одговор: x - 3 0 = y + 2 - 4
Во случај кога е потребно да се напише равенка на права од формата A x + B y + C = 0, а се дадени параметарски равенки на права на рамнина, потребно е прво да се направи премин кон канонската равенка, а потоа и до општата равенка на правата. Ајде да ја запишеме целата низа на дејства:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y ⇔ ⇔ a y · (x - x 1) = a x (y - y 1) ⇔ A x + B y + C = 0
Пример 3
Потребно е да се запише општата равенка на права линија ако се дадени параметарските равенки што ја дефинираат: x = - 1 + 2 · λ y = - 3 · λ
Решение
Прво, да ја направиме транзицијата кон канонската равенка:
x = - 1 + 2 λ y = - 3 λ ⇔ λ = x + 1 2 λ = y - 3 ⇔ x + 1 2 = y - 3
Добиената пропорција е идентична со еднаквоста - 3 · (x + 1) = 2 · y. Да ги отвориме заградите и да ја добиеме општата равенка на правата: - 3 x + 1 = 2 y ⇔ 3 x + 2 y + 3 = 0.
Одговор: 3 x + 2 y + 3 = 0
Следејќи ја горната логика на дејства, за да се добие равенка на права со аголен коефициент, равенка на права во отсечки или нормална равенка на права, потребно е да се добие општата равенка на правата, а потоа изврши понатамошна транзиција од него.
Сега разгледајте го обратното дејство: пишување параметарски равенки на права со различна дадена форма на равенките од оваа права.
Наједноставниот премин: од канонската равенка до параметарските. Нека е дадена канонска равенка од формата: x - x 1 a x = y - y 1 a y. Да земеме дека секоја од односите на оваа еднаквост е еднаква на параметарот λ:
x - x 1 a x = y - y 1 a y = λ ⇔ λ = x - x 1 a x λ = y - y 1 a y
Да ги решиме добиените равенки за променливите x и y:
x = x 1 + a x · λ y = y 1 + a y · λ
Пример 4
Потребно е да се запишат параметарските равенки на правата ако е позната канонската равенка на правата на рамнината: x - 2 5 = y - 2 2
Решение
Да ги изедначиме деловите од познатата равенка со параметарот λ: x - 2 5 = y - 2 2 = λ. Од добиената еднаквост ги добиваме параметарските равенки на правата: x - 2 5 = y - 2 2 = λ ⇔ λ = x - 2 5 λ = y - 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ
Одговор: x = 2 + 5 λ y = 2 + 2 λ
Кога е неопходно да се направи премин кон параметарски равенки од дадена општа равенка на права, равенка на права со аголен коефициент или равенка на права во отсечки, потребно е првобитната равенка да се доведе до канонската еден, а потоа направете премин кон параметарски равенки.
Пример 5
Потребно е да се запишат параметарските равенки на права со позната општа равенка на оваа права: 4 x - 3 y - 3 = 0.
Решение
Да ја трансформираме дадената општа равенка во равенка со канонска форма:
4 x - 3 y - 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4
Да ги изедначиме двете страни на еднаквоста со параметарот λ и да ги добиеме бараните параметарски равенки на права линија:
x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 λ y = - 1 3 + 4 λ
Одговор: x = 3 λ y = - 1 3 + 4 λ
Примери и задачи со параметарски равенки на права на рамнина
Да ги разгледаме најчестите типови проблеми користејќи параметарски равенки на права на рамнина во правоаголен координатен систем.
- Во задачите од првиот тип се дадени координатите на точките, без разлика дали припаѓаат или не на права опишана со параметарски равенки.
Решението на ваквите проблеми се заснова на следниот факт: броевите (x, y), определени од параметарските равенки x = x 1 + a x · λ y = y 1 + a y · λ за некоја реална вредност λ, се координатите на точка која припаѓа на правата што е опишана овие параметарски равенки.
Пример 6
Потребно е да се одредат координатите на точка што лежи на права одредена со параметарските равенки x = 2 - 1 6 · λ y = - 1 + 2 · λ за λ = 3.
Решение
Да ја замениме познатата вредност λ = 3 во дадените параметарски равенки и да ги пресметаме бараните координати: x = 2 - 1 6 3 y = - 1 + 2 3 ⇔ x = 1 1 2 y = 5
Одговор: 1 1 2 , 5
Можна е и следната задача: нека биде дадена точка M 0 (x 0 , y 0) на рамнина во правоаголен координатен систем и треба да одредите дали оваа точка припаѓа на линијата опишана со параметарските равенки x = x 1 + a x · λ y = y 1 + a y · λ .
За да се реши таков проблем, потребно е да се заменат координатите на дадена точка во познатите параметарски равенки на права линија. Ако се утврди дека е можна вредност на параметарот λ = λ 0 за која се вистинити двете параметарски равенки, тогаш дадената точка припаѓа на дадената права линија.
Пример 7
Дадени се точките M 0 (4, - 2) и N 0 (- 2, 1). Потребно е да се определи дали припаѓаат на линијата дефинирана со параметарските равенки x = 2 · λ y = - 1 - 1 2 · λ .
Решение
Да ги замениме координатите на точката M 0 (4, - 2) во дадените параметарски равенки:
4 = 2 λ - 2 = - 1 - 1 2 λ ⇔ λ = 2 λ = 2 ⇔ λ = 2
Заклучуваме дека точката M 0 припаѓа на дадената права, бидејќи одговара на вредноста λ = 2.
2 = 2 λ 1 = - 1 - 1 2 λ ⇔ λ = - 1 λ = - 4
Очигледно не постои таков параметар λ на кој ќе одговара точката N 0. Со други зборови, дадената права линија не поминува низ точката N 0 (- 2, 1).
Одговор:точката M 0 припаѓа на дадена права; точката N 0 не припаѓа на дадената права.
- Кај проблемите од вториот тип, потребно е да се состават параметарски равенки на права на рамнина во правоаголен координатен систем. Наједноставниот пример за таков проблем (со познати координати на точката на правата и векторот на насока) беше разгледан погоре. Сега да погледнеме примери во кои прво треба да ги најдеме координатите на векторот водич, а потоа да ги запишеме параметарските равенки.
Дадена точка М 1 1 2 , 2 3 . Потребно е да се состават параметарски равенки на права што минува низ оваа точка и паралелна со правата x 2 = y - 3 - 1.
Решение
Според условите на задачата, правата линија по чија равенка треба да се понапредиме, е паралелна со правата x 2 = y - 3 - 1. Потоа, како вектор на насока на права што минува низ дадена точка, можно е да се користи векторот на насоката на правата x 2 = y - 3 - 1, кој го пишуваме во форма: a → = (2, - 1 ) . Сега се познати сите потребни податоци за да се состават потребните параметарски равенки:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + (- 1) · λ ⇔ x = 1 2 + x · λ y = 2 3 - λ
Одговор: x = 1 2 + x · λ y = 2 3 - λ.
Пример 9
Дадена е точка М 1 (0, - 7). Потребно е да се запишат параметарските равенки на правата што минува низ оваа точка нормално на правата 3 x – 2 y – 5 = 0.
Решение
Како вектор на насока на правата линија, чија равенка мора да се состави, можно е да се земе нормалниот вектор на правата линија 3 x – 2 y – 5 = 0. Неговите координати се (3, - 2). Да ги запишеме бараните параметарски равенки на права линија:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = - 7 + (- 2) · λ ⇔ x = 3 · λ y = - 7 - 2 · λ
Одговор: x = 3 λ y = - 7 - 2 λ
- Кај проблемите од третиот тип, потребно е да се направи премин од параметарски равенки на дадена права на други видови равенки што ја одредуваат. Разговаравме за решението на слични примери погоре; ќе дадеме уште еден.
Дадена е права линија на рамнина во правоаголен координатен систем, дефинирана со параметарските равенки x = 1 - 3 4 · λ y = - 1 + λ. Неопходно е да се најдат координатите на кој било нормален вектор од оваа права.
Решение
За да ги одредиме потребните координати на нормалниот вектор, ќе направиме премин од параметарски равенки во општата равенка:
x = 1 - 3 4 λ y = - 1 + λ ⇔ λ = x - 1 - 3 4 λ = y + 1 1 ⇔ x - 1 - 3 4 = y + 1 1 ⇔ ⇔ 1 x - 1 = - 3 4 y + 1 ⇔ x + 3 4 y - 1 4 = 0
Коефициентите на променливите x и y ни ги даваат бараните координати на нормалниот вектор. Така, нормалниот вектор на правата x = 1 - 3 4 · λ y = - 1 + λ има координати 1, 3 4.
Одговор: 1 , 3 4 .
Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter