Паралелограм е четириаголник чии спротивни страни се паралелни во парови (сл. 233).
За произволен паралелограм важат следните својства:
1. Спротивните страни на паралелограмот се еднакви.
Доказ. Во паралелограмот ABCD ја цртаме дијагоналата AC. Триаголниците ACD и AC B се еднакви, бидејќи имаат заедничка страна AC и два пара еднакви агли, во непосредна близина на него:
(како попречни агли со паралелни прави AD и BC). Ова значи, како и страните на еднаквите триаголници кои лежат спроти еднакви агли, што требаше да се докаже.

2. Спротивните агли на паралелограм се еднакви:
3. Соседни агли на паралелограм, т.е., агли соседни на едната страна, собираат итн.
Доказот за својствата 2 и 3 веднаш се добива од својствата на аглите за паралелни прави.
4. Дијагоналите на паралелограмот се преполовуваат на нивната пресечна точка. Со други зборови,
Доказ. Триаголниците AOD и BOC се складни, бидејќи нивните страни AD и BC се еднакви (својство 1) и аглите соседни до нив (како вкрстени агли за паралелни прави). Од тука произлегува дека соодветните страни на овие триаголници се еднакви: AO, што требаше да се докаже.
Секое од овие четири својства карактеризира паралелограм, или, како што велат, е негово карактеристично својство, т.е., секој четириаголник што има барем едно од овие својства е паралелограм (и, според тоа, ги има сите други три својства).
Дозволете ни да го спроведеме доказот за секој имот посебно.
1". Ако спротивните страни на четириаголникот се еднакви во парови, тогаш тоа е паралелограм.
Доказ. Нека четириаголникот ABCD има страни AD и BC, AB и CD соодветно еднакви (сл. 233). Ајде да ја нацртаме дијагоналата AC. Триаголниците ABC и CDA ќе бидат складни како да имаат три пара еднакви страни.
Но тогаш аглите BAC и DCA се еднакви и . Паралелизмот на страните BC и AD следи од еднаквоста на аглите CAD и ACB.
2. Ако четириаголник има два пара спротивни агли еднакви, тогаш тој е паралелограм.
Доказ. Нека . Оттогаш и двете страни AD и BC се паралелни (врз основа на паралелизам на правите).
3. Формулацијата и доказот ги оставаме на читателот.
4. Ако дијагоналите на четириаголник се преполовуваат на точката на пресек, тогаш четириаголникот е паралелограм.
Доказ. Ако AO = OS, BO = OD (сл. 233), тогаш триаголниците AOD и BOC се еднакви, бидејќи имаат еднакви агли (вертикални!) на темето O, затворени помеѓу парови на еднакви страни AO и CO, BO и DO. Од еднаквоста на триаголниците заклучуваме дека страните AD и BC се еднакви. Страните AB и CD се исто така еднакви, а четириаголникот излегува дека е паралелограм според карактеристичното својство G.
Така, за да се докаже дека даден четириаголник е паралелограм, доволно е да се потврди валидноста на кое било од четирите својства. Читателот е поканет самостојно да докаже уште едно карактеристично својство на паралелограм.

5. Ако четириаголник има пар еднакви, паралелни страни, тогаш тој е паралелограм.
Понекогаш секој пар паралелни страни на паралелограм се нарекуваат негови основи, а потоа другите две се нарекуваат странични страни. Права отсечка нормална на две страни на паралелограм, затворена меѓу нив, се нарекува висина на паралелограмот. Паралелограм на Сл. 234 има висина h нацртана на страните AD и BC, неговата втора висина е претставена со отсечката .
Паралелограм е четириаголник чии спротивни страни се паралелни, т.е. лежат на паралелни линии
Својства на паралелограм: 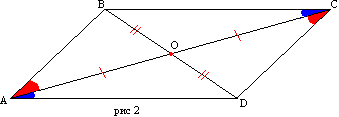 Теорема 22.
Спротивните страни на паралелограмот се еднакви.
Теорема 22.
Спротивните страни на паралелограмот се еднакви.
Доказ. Во паралелограмот ABCD цртаме дијагонала AC. Триаголниците ACD и ACB се складни, бидејќи имаат заедничка страна AC и два пара еднакви агли. непосредно до него: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (како попречни агли со паралелни прави AD и BC). Тоа значи дека AB = CD и BC = AD, како соодветни страни на еднакви триаголници итн. Еднаквоста на овие триаголници ја подразбира и еднаквоста соодветните аглитриаголници:
Теорема 23.
Спротивните агли на паралелограмот се еднакви: ∠ A=∠ C и ∠ B=∠ D.
Еднаквоста на првиот пар доаѓа од еднаквоста на триаголниците ABD и CBD, а вториот - ABC и ACD.
Теорема 24.
Соседни агли на паралелограм, т.е. аглите во непосредна близина на едната страна додаваат до 180 степени.
Тоа е така затоа што тие се внатрешни еднострани агли.
Теорема 25.
Дијагоналите на паралелограмот се преполовуваат на нивната пресечна точка.
Доказ. Размислете за триаголниците BOC и AOD. Според првото својство AD=BC ∠ OAD=∠ OCB и ∠ ODA=∠ OBC лежи попречно за паралелни прави AD и BC. Според тоа, триаголниците BOC и AOD се еднакви по страничните и соседните агли. Ова значи BO=OD и AO=OS, како соодветните страни на еднакви триаголници, итн.
Знаци на паралелограм
Теорема 26.
Ако спротивните страни на четириаголникот се еднакви во парови, тогаш тоа е паралелограм.
Доказ. Нека четириаголникот ABCD има страни AD и BC, AB и CD соодветно еднакви (сл. 2). Ајде да ја нацртаме дијагоналата AC. Триаголниците ABC и ACD се еднакви на три страни. Тогаш аглите BAC и DCA се еднакви и, според тоа, AB е паралелен со CD. Паралелизмот на страните BC и AD следи од еднаквоста на аглите CAD и ACB.
Теорема 27.
Ако спротивните агли на четириаголник се еднакви во парови, тогаш тоа е паралелограм.
Нека ∠ A=∠ C и ∠ B=∠ D. Бидејќи ∠ A+∠ B+∠ C+∠ D=360 o, потоа ∠ A+∠ B=180 o и страните AD и BC се паралелни (врз основа на паралелизам на прави). Ќе ја докажеме и паралелизмот на страните AB и CD и ќе заклучиме дека ABCD е паралелограм по дефиниција.
Теорема 28.
Ако соседните агли на четириаголник, т.е. Аглите во непосредна близина на едната страна се собираат до 180 степени, тогаш тоа е паралелограм.
Ако внатрешните еднострани агли се соберат до 180 степени, тогаш правите линии се паралелни. Значи AB е паралелен со CD и BC е паралелен со AD. Излегува дека четириаголник е паралелограм по дефиниција.
Теорема 29.
Ако дијагоналите на четириаголник се преполоват една со друга на точката на пресек, тогаш четириаголникот е паралелограм.
Доказ. Ако AO = OC, BO = OD, тогаш триаголниците AOD и BOC се еднакви, бидејќи имаат еднакви (вертикални) агли на темето O, затворени помеѓу парови на еднакви страни. Од еднаквоста на триаголниците заклучуваме дека AD и BC се еднакви. Страните AB и CD се исто така еднакви, а четириаголникот излегува дека е паралелограм според критериумот 1.
Теорема 30.
Ако четириаголник има пар еднакви, паралелни страни, тогаш тој е паралелограм.
Нека страните AB и CD на четириаголникот ABCD се паралелни и еднакви. Ајде да нацртаме дијагонали AC и BD. Од паралелизмот на овие прави произлегува дека попречните агли ABO = CDO и BAO = OCD се еднакви. Триаголниците ABO и CDO се еднакви по страничните и соседните агли. Затоа AO=OS, VO=ОD, т.е. Дијагоналите се поделени на половина со пресечната точка и четириаголникот излегува дека е паралелограм според критериумот 4.
Во геометријата се разгледуваат посебни случаи на паралелограми.
Дефиниција
Паралелограме четириаголник чии спротивни страни се паралелни во парови.
Точката на пресек на дијагоналите на паралелограм се нарекува центар.
Својства на паралелограм:
- Збирот на кои било два соседни агли на паралелограм е $180^(\circ)$, а спротивните агли се еднакви.
- Спротивните страни на паралелограмот се еднакви.
- Дијагоналите на паралелограмот се сечат и пресечат на пресечната точка.
Доказ
Нека е даден паралелограм $ABCD$.
1. Забележете дека соседните агли $A$ и $B$ на паралелограм се еднострани внатрешни агли со паралелни прави $AD$ и $BC$ и секанта $AB$, односно нивниот збир е еднаков на $180^ \circ$. Исто и за други парови агли.
Ако $\агол A + \агол B=180^\circ$ и $\агол C + \агол B=180^\circ$, тогаш $\агол A = \агол C$. Слично на тоа, $\агол B = \агол D$.
2. Размислете за триаголниците $ABC$ и $CDA$. Од паралелизмот на спротивните страни на паралелограмот следува дека $\агол BAC=\агол DCA$ и $\агол BCA=\агол DAC$. Бидејќи $AC$ е вообичаен, тогаш триаголниците $ABC$ и $CDA$ се еднакви според вториот критериум. Од еднаквоста на триаголниците произлегува дека $AB=CD$ и $BC=AD$.
3. Бидејќи паралелограмот е конвексен четириаголник, неговите дијагонали се сечат. Нека $O$ е пресечната точка. Од паралелизмот на страните $BC$ и $AD$ на паралелограмот следува дека $\агол OAD=\агол OCB$ и $\агол ODA=\агол OBC$. Земајќи ја предвид еднаквоста $BC=AD$, добиваме дека триаголниците $AOD$ и $COB$ се еднакви според вториот критериум. Затоа, $AO=CO$ и $DO=BO$, по потреба.

Знаци на паралелограм:
- Ако во четириаголник збирот на кои било два соседни агли е $180^(\circ)$, тогаш овој четириаголник е паралелограм.
- Ако во четириаголник спротивните агли се еднакви во парови, тогаш овој четириаголник е паралелограм.
- Ако во четириаголник спротивните страни се еднакви во парови, тогаш овој четириаголник е паралелограм.
- Ако две страни на четириаголник се еднакви и паралелни, тогаш четириаголникот е паралелограм.
- Ако дијагоналите на четириаголник се пресечени со нивната пресечна точка, тогаш четириаголникот е паралелограм.
Доказ
Нека $ABCD$ е четириаголник.
1. Забележете дека соседните агли $A$ и $B$ се еднострани внатрешни агли со прави линии $AD$ и $BC$ и трансверзална $AB$. Бидејќи нивниот збир е $180^\circ$, тогаш линиите $AD$ и $BC$ се паралелни. Слично на друг пар линии, односно $ABCD$ е паралелограм по дефиниција.
2. Забележете дека $\агол A + \агол B + \агол C + \агол D=360^\circ$. Ако $\агол A = \агол C$, и $\агол B = \агол D$, тогаш $\агол A + \агол B=180^\circ$ и слично за други парови соседни агли. Следно го користиме претходниот знак.
3. Размислете за триаголниците $ABC$ и $CDA$. Бидејќи $AC$ е вообичаено, од еднаквоста на спротивните страни на паралелограмот произлегува дека триаголниците $ABC$ и $CDA$ се еднакви според третиот критериум. Според тоа, $\агол BAC=\агол DCA$ и $\агол BCA=\агол DAC$, што подразбира паралелизам на спротивните страни.
4. Нека $BC$ и $AD$ се еднакви и паралелни. Размислете за триаголниците $ABC$ и $CDA$. Од паралелизмот на правите произлегува дека $\агол BCA=\агол DAC$. Бидејќи $AC$ е општо и $BC=AD$, тогаш триаголниците $ABC$ и $CDA$ се еднакви според првиот критериум. Затоа, $AB=CD$. Следно го користиме претходниот знак.
5. Нека $O$ е пресечната точка на дијагоналите и $AO=CO$ и $DO=BO$ Земајќи ја предвид еднаквоста на вертикалните агли, добиваме дека триаголниците $AOD$ и $COB$ се еднакви според првиот критериум. Затоа, $\angle OAD=\angle OCB$, што подразбира паралелизам на $BC$ и $AD$. Исто и за другиот пар страни.
Дефиниција
Се нарекува четириаголник кој има три прави агли правоаголник.
Карактеристики на правоаголник:
- Дијагоналите на правоаголникот се еднакви.
Доказ
Нека е даден правоаголник $ABCD$. Бидејќи правоаголникот е паралелограм, неговите спротивни страни се еднакви. Тогаш правоаголните триаголници $ABD$ и $DCA$ се еднакви на две кати, што значи дека $BD=AC$.
Карактеристики на правоаголник:
- Ако паралелограмот има прав агол, тогаш овој паралелограм е правоаголник.
- Ако дијагоналите на паралелограмот се еднакви, тогаш овој паралелограм е правоаголник.
Доказ
1. Ако еден од аглите на паралелограмот е правилен, тогаш, имајќи предвид дека збирот на соседните агли е $180^(\circ)$, добиваме дека и останатите агли се прави.
2. Нека дијагоналите $AC$ и $BD$ се еднакви во паралелограмот $ABCD$. Земајќи ја предвид еднаквоста на спротивните страни $AB$ и $DC$, добиваме дека триаголниците $ABD$ и $DCA$ се еднакви според третиот критериум. Затоа, $\angle BAD=\angle CDA$, односно тие се прави. Останува да се користи претходниот знак.
Дефиниција
Се нарекува четириаголник во кој сите страни се еднакви дијамант
Својства на ромб:
- Дијагоналите на ромбот се меѓусебно нормални и се симетрали на неговите агли.
Доказ
Нека дијагоналите $AC$ и $BD$ во ромбот $ABCD$ се сечат во точката $O$. Бидејќи ромбот е паралелограм, $AO=OC$. Ајде да размислиме рамнокрак триаголник$ABC$. Со оглед на тоа што $AO$ е средната вредност што се влече до основата, тоа е симетралата и висината, што се бараше.
Знаци на дијамант:
- Ако дијагоналите на паралелограмот се меѓусебно нормални, тогаш овој паралелограм е ромб.
- Ако дијагоналата на паралелограмот е симетрала на неговиот агол, тогаш овој паралелограм е ромб.
Доказ
Нека паралелограмот $ABCD$ има дијагонали $AC$ и $BD$ кои се сечат во точката $O$. Размислете за триаголникот $ABC$.
1. Ако дијагоналите се нормални, тогаш $BO$ е средина и висина на триаголникот.
2. Ако дијагоналата $BD$ ја содржи симетралата на аголот $ABC$, тогаш $BO$ е медијаната и симетралата во триаголникот.
Во двата случаи, откриваме дека триаголникот $ABC$ е рамнокрак, а во паралелограм соседните страни се еднакви. Затоа, тоа е ромб, што и се бараше.
Дефиниција
Се вика правоаголник чии две соседни страни се еднакви квадрат.
Знаци на квадрат:
- Ако ромб има прав агол, тогаш тој ромб е квадрат.
- Ако ромбот има еднакви дијагонали, тогаш ромбот е квадрат.
Доказ
Ако паралелограмот има прав агол или еднакви дијагонали, тогаш тој е правоаголник. Ако четириаголник е правоаголник и ромб, тогаш тоа е квадрат.
Паралелограм е четириаголник чии спротивни страни се паралелни во парови. Плоштината на паралелограм е еднаква на производот на неговата основа (а) и висината (h). Неговата површина можете да ја најдете и преку две страни и агол и преку дијагонали.
Својства на паралелограм
1. Спротивните страни се идентични
Прво, да ја нацртаме дијагоналата \(AC\) . Добиваме два триаголници: \(ABC\) и \(ADC\).
Бидејќи \(ABCD\) е паралелограм, следново е точно:
\(АД || п.н.е. \Десна стрелка \агол 1 = \агол 2\)како да лежи вкрстено.
\(AB || ЦД \Десна стрелка \агол3 = \агол 4\)како да лежи вкрстено.
Затоа, (според вториот критериум: и \(AC\) е вообичаено).
И тоа значи \(\триаголник ABC = \триаголник ADC\), потоа \(AB = CD\) и \(AD = BC\) .
2. Спротивните агли се идентични

Според доказот својства 1Ние го знаеме тоа \(\агол 1 = \агол 2, \агол 3 = \агол 4\). Така, збирот на спротивните агли е: \(\агол 1 + \агол 3 = \агол 2 + \агол 4\). Со оглед на тоа \(\триаголник ABC = \триаголник ADC\)добиваме \(\агол A = \агол C \) , \(\агол B = \агол D \) .
3. Дијагоналите се делат на половина со пресечната точка

Од страна на имот 1знаеме дека спротивните страни се идентични: \(AB = CD\) . Уште еднаш, забележете ги вкрстените еднакви агли.
Така е јасно дека \(\триаголник AOB = \триаголник COD\)според вториот знак за еднаквост на триаголниците (два агли и страната меѓу нив). Тоа е, \(BO = OD\) (спроти аглите \(\агол 2\) и \(\агол 1\) ) и \(AO = OC\) (спроти аглите \(\агол 3\) и \( \агол 4\) соодветно).
Знаци на паралелограм
Ако во вашиот проблем е присутна само една карактеристика, тогаш фигурата е паралелограм и можете да ги користите сите својства на оваа фигура.
За подобро меморирање, имајте предвид дека тестот за паралелограм ќе одговори на следново прашање - "Како да дознаете?". Односно од каде знаеш што поставена фигураова е паралелограм.
1. Паралелограм е четириаголник чии две страни се еднакви и паралелни
\(AB = CD\) ; \(AB || ЦД \Десна стрелка ABCD\)- паралелограм.

Ајде да погледнеме подетално. Зошто \(АД || п.н.е. \) ?
\(\триаголник ABC = \триаголник ADC\)Од страна на имот 1: \(AB = CD \) , \(\агол 1 = \агол 2 \) лежи попречно кога \(AB \) и \(CD \) и секантата \(AC \) се паралелни.
Но ако \(\триаголник ABC = \триаголник ADC\), потоа \(\агол 3 = \агол 4 \) (лежи спроти \(АД || п.н.е. \) (\(\агол 3 \) и \(\агол 4 \) - оние што лежат попречно се исто така еднакви).
Првиот знак е точен.
2. Паралелограм е четириаголник чии спротивни страни се еднакви
\(AB = CD \) , \(AD = BC \Десна стрелка ABCD \) е паралелограм.

Ајде да го разгледаме овој знак. Ајде повторно да ја нацртаме дијагоналата \(AC\).
Од страна на имот 1\(\триаголник ABC = \триаголник ACD\).
Го следи тоа: \(\агол 1 = \агол 2 \Десна стрелка AD || п.н.е. \)И \(\агол 3 = \агол 4 \Десна стрелка AB || ЦД\), односно \(ABCD\) е паралелограм.
Вториот знак е точен.
3. Паралелограм е четириаголник чии спротивни агли се еднакви
\(\агол A = \агол C\) , \(\агол B = \агол D \Десна стрелка ABCD\)- паралелограм.

\(2 \алфа + 2 \бета = 360^(\circ) \)(бидејќи \(\агол A = \агол C\) , \(\агол B = \агол D\) по услов).
Излегува,. Но, \(\алфа \) и \(\beta \) се внатрешни еднострани во секантата \(AB \) .
И што \(\алфа + \бета = 180^(\circ) \)исто така вели дека \(АД || п.н.е. \) .
Доказ
Пред сè, да ја нацртаме дијагоналата AC. Добиваме два триаголници: ABC и ADC.

Бидејќи ABCD е паралелограм, следново е точно:
АД || BC \Десна стрелка \агол 1 = \агол 2како да лежи вкрстено.
AB || CD\Rightarrow\angle3 =\angle 4како да лежи вкрстено.
Затоа, \триаголник ABC = \триаголник ADC (според вториот критериум: и AC е вообичаено).
И, според тоа, \триаголник ABC = \триаголник ADC, потоа AB = CD и AD = BC.
Докажано!
2. Спротивните агли се идентични.

Доказ
Според доказот својства 1Ние го знаеме тоа \агол 1 = \агол 2, \агол 3 = \агол 4. Така, збирот на спротивните агли е: \агол 1 + \агол 3 = \агол 2 + \агол 4. Имајќи предвид дека \триаголник ABC = \триаголник ADC добиваме \агол A = \агол C , \агол B = \агол D .
Докажано!
3. Дијагоналите се делат на половина со пресечната точка.

Доказ
Ајде да нацртаме друга дијагонала.

Од страна на имот 1знаеме дека спротивните страни се идентични: AB = CD. Уште еднаш, забележете ги вкрстените еднакви агли.
Така, јасно е дека \триаголник AOB = \триаголник COD според вториот критериум за еднаквост на триаголниците (два агли и страната меѓу нив). Тоа е, BO = OD (наспроти аглите \агол 2 и \агол 1) и AO = OC (наспроти аглите \агол 3 и \агол 4, соодветно).

Докажано!
Знаци на паралелограм
Ако во вашиот проблем е присутна само една карактеристика, тогаш фигурата е паралелограм и можете да ги користите сите својства на оваа фигура.
За подобро меморирање, забележете дека знакот паралелограм ќе одговори на следново прашање - "Како да дознаете?". Односно, како да дознаеме дека дадената фигура е паралелограм.
1. Паралелограм е четириаголник чии две страни се еднакви и паралелни.

AB = CD ; AB || CD\Rightarrow ABCD е паралелограм.
Доказ
Ајде да погледнеме подетално. Зошто АД || п.н.е.?

\триаголник ABC = \триаголник ADC од имот 1: AB = CD, AC - заеднички и \агол 1 = \агол 2 лежи попречно со паралелни AB и CD и секантна AC.
Но, ако \триаголник ABC = \триаголник ADC , тогаш \аголот 3 = \аголот 4 (лежи спроти AB и CD, соодветно). И затоа АД || BC (\агол 3 и \агол 4 - оние што лежат попречно се исто така еднакви).

Првиот знак е точен.
2. Паралелограм е четириаголник чии спротивни страни се еднакви.

AB = CD, AD = BC \Rightarrow ABCD е паралелограм.
Доказ
Ајде да го разгледаме овој знак. Ајде повторно да ја нацртаме дијагоналата AC.

Од страна на имот 1\триаголник ABC = \триаголник ACD .

Го следи тоа: \агол 1 = \агол 2 \Десна стрелка АД || п.н.е.И \агол 3 = \агол 4 \Десна стрелка AB || ЦД, односно ABCD е паралелограм.
Вториот знак е точен.
3. Паралелограм е четириаголник чии спротивни агли се еднакви.

\агол A = \агол C, \агол B = \агол D \Десна стрелка ABCD- паралелограм.
Доказ

2 \алфа + 2 \бета = 360^(\circ)(бидејќи ABCD е четириаголник, и \агол A = \агол C , \агол B = \агол D по услов).
Излегува дека \алфа + \бета = 180^(\circ) . Но, \alpha и \beta се внатрешни еднострани во секантата AB.
И фактот дека \alpha + \beta = 180^(\circ) исто така значи дека AD || п.н.е.
Покрај тоа, \alpha и \beta се внатрешни еднострани во секантата AD . А тоа значи AB || ЦД.
Третиот знак е точен.
4. Паралелограм е четириаголник чии дијагонали се поделени на половина со точката на пресек.

AO = OC ; BO = OD\Десна стрелка паралелограм.
Доказ

BO = OD; AO = OC , \агол 1 = \агол 2 како вертикален \Десна стрелка \триаголник AOB = \триаголник COD, \Десна стрелка \агол 3 = \агол 4, и \Rightarrow AB || ЦД.
Слично BO = OD; AO = OC, \агол 5 = \агол 6 \десна стрелка \триаголник AOD = \триаголник BOC \Десна стрелка \агол 7 = \агол 8, и \Rightarrow AD || п.н.е.
Четвртиот знак е точен.







