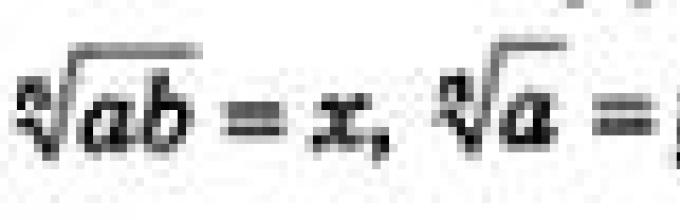Треба да се запознаеме со својствата на оваа операција, што ќе го направиме во овој дел.
Сите својства се формулирани и докажани само за не-негативни вредности на променливите содржани под знаците на корените.
Доказ.Да ја воведеме следната нотација: ![]() Треба да докажеме дека за ненегативни броеви x, y, z важи еднаквоста x-yz.
Треба да докажеме дека за ненегативни броеви x, y, z важи еднаквоста x-yz.
Бидејќи
Значи, ако моќите на два ненегативни броја се еднакви, а експонентите се еднакви, тогаш основите се еднакви степени; Тоа значи дека од еднаквоста x n =(уz) n произлегува дека x-yz, и тоа требаше да се докаже.
Да дадеме кратко резиме на доказот на теоремата.

Белешки:
1.
Теоремата 1 останува валидна за случајот кога радикалниот израз е производ на повеќе од два ненегативни броја.
2.
Теоремата 1 може да се формулира со употреба на конструкцијата „ако...тогаш“ (како што е вообичаено за теоремите во математиката) Да ја дадеме соодветната формулација: ако a и b се ненегативни броеви, тогаш важи еднаквоста. како ќе ја формулираме следната теорема.

Кратка (иако непрецизна) формулација која е попогодна за употреба во пракса: коренот на дропкие еднаква на фракцијата на корените.
Доказ.Ќе дадеме кратко резиме на доказот за теорема 2, а вие може да се обидете да дадете соодветни коментари слични на оние дадени во доказот за теорема 1.

ВИЕ, се разбира, забележавте дека докажаните две својства на корените n-ти степенпретставуваат генерализација на својства кои ви се познати од курсот алгебра за 8 одделение квадратни корени. И да има други имоти корени n-тинемаше диплома, тогаш сè ќе беше едноставно (и не многу интересно). Всушност, има уште неколку интересни и важни својства за кои ќе разговараме во овој пасус. Но, прво, да погледнеме неколку примери за користење на теоремите 1 и 2.
Пример 1.Пресметај
Решение.Користејќи го првото својство на корените (теорема 1), добиваме:
Забелешка 3.Овој пример, се разбира, можете да го решите поинаку, особено ако имате при рака микрокалкулатор: помножете ги броевите 125, 64 и 27, а потоа земете го коцканиот корен од добиениот производ. Но, гледате, предложеното решение е „поинтелигентно“.
Пример 2.Пресметај
Решение.Ајде да се обратиме мешан бројво неправилна дропка.
Имаме Користејќи го второто својство на корените (теорема 2), добиваме:
![]()
Пример 3.Пресметајте: ![]()
Решение.Секоја формула во алгебрата, како што добро знаете, се користи не само „од лево кон десно“, туку и „од десно кон лево“. Така, првото својство на корените значи дека тие можат да бидат претставени во форма и, обратно, да се заменат со изразот. Истото важи и за второто својство на корените. Земајќи го ова предвид, ајде да ги извршиме пресметките:
Пример 4.Следете ги овие чекори:
Решение, а) Имаме:
б) Теорема 1 ни овозможува да множиме само корени од ист степен, т.е. само корени со ист индекс. Овде се предлага да се помножи вториот корен од бројот a со третиот корен од истиот број. Сè уште не знаеме како да го направиме ова. Ајде да се вратиме на овој проблем подоцна.
Ајде да продолжиме да ги проучуваме својствата на радикалите.
Со други зборови, за да се подигне корен на природна моќ, доволно е да се подигне радикалниот израз на оваа моќ.
Ова е последица на теоремата 1. Всушност, на пример, за k = 3 добиваме: Можеме да расудуваме на ист начин во случај на која било друга природна вредност на експонентот k.
Со други зборови, за да се извлече корен од корен, доволно е да се умножат индикаторите на корените.
На пример,
Доказ.Како и во теорема 2, ќе дадеме кратко резиме на доказот, а вие може да се обидете сами да ги дадете соодветните коментари, слични на оние дадени во доказот на теоремата 1.

Забелешка 4.Ајде да земеме здив. Што научивме од теоремите што ги докажавме? Научивме дека на корените може да се извршат четири операции: множење, делење, степенување и вадење корен (од коренот). Но, што е со собирањето и одземањето на корените? Нема шанси. Зборувавме за ова уште во 8-мо одделение за операцијата на вадење квадратен корен.
На пример, наместо тоа не можете да напишете Навистина, но очигледно е дека бидете внимателни!
Можеби најинтересното својство на корените е она што ќе се дискутира во следната теорема. Со оглед на посебното значење на ова својство, ќе си дозволиме да го разбиеме одредениот стил на формулации и докази развиени во овој дел, така што формулацијата на теоремата 5 е малку „помека“ и нејзиното докажување е појасно.
На пример:
(показателите за коренот и радикалниот израз беа поделени со 4);
(показателите за коренот и радикалниот израз беа поделени со 3);
(показателите за коренот и радикалниот израз беа помножени со 2).
Доказ.Да ја означиме левата страна на еднаквоста што се докажува со буквата. Тогаш, со дефиниција за корен, еднаквоста мора да се задоволи
Да ја означиме десната страна на идентитетот што се докажува со буквата y:
Потоа, по дефиниција за корен, еднаквоста
Да ги подигнеме двете страни на последната еднаквост на иста моќност p; добиваме:
Значи (види еднаквости (1) и (2)),
![]()
Споредувајќи ги овие две еднаквости, доаѓаме до заклучок дека x nр = y nр, а со тоа и x = y, што требаше да се докаже.
Докажаната теорема ќе ни овозможи да го решиме проблемот што го најдовме погоре при решавање на примерот 5, каде што беше неопходно да се множат корените со различни експоненти:
Вака обично расудуваат во вакви случаи.
1) Според теорема 5, во изразот е можно да се помножат и индексот на коренот (т.е. бројот 2) и експонентот на радикалниот израз (т.е. бројот 1) со иста работа природен број. Искористувајќи го ова, ги множиме двата показатели со 3; добиваме:
2) Според теорема 5, во изразот е можно да се помножат и експонентот на коренот (т.е. бројот 3) и експонентот на радикалниот израз (т.е. бројот 1) со ист природен број. Искористувајќи го ова, ги множиме двата показатели со 2; добиваме:
3) Бидејќи добивме корени од истиот 6-ти степен, можеме да ги помножиме:
Забелешка 5.Дали заборавивте дека сите својства на корените за кои разговаравме во овој дел беа земени предвид само за случајот кога променливите земаат само ненегативни вредности? Зошто мораше да се направи такво ограничување? Бидејќи n-ти коренстепени од негативен бројне секогаш има смисла - тоа е дефинирано само за непарни вредности на n. За такви вредности на коренскиот експонент, разгледаните својства на корените се вистинити и во случај на негативни радикални изрази.
А.Г. Мордкович Алгебра 10 одделение
Содржина на лекцијата белешки за лекцијатаподдршка на рамка лекција презентација методи забрзување интерактивни технологии Вежбајте задачи и вежби работилници за самотестирање, обуки, случаи, потраги прашања за дискусија за домашни задачи реторички прашања од ученици Илустрации аудио, видео клипови и мултимедијафотографии, слики, графики, табели, дијаграми, хумор, анегдоти, шеги, стрипови, параболи, изреки, крстозбори, цитати Додатоци апстрактистатии трикови за љубопитните креветчиња учебници основни и дополнителен речник на поими друго Подобрување на учебниците и лекциитекорекција на грешки во учебникотажурирање фрагмент во учебник, елементи на иновација во лекцијата, замена на застарените знаења со нови Само за наставници совршени лекции календарски планза една година насокипрограми за дискусија Интегрирани лекцииОдржувањето на вашата приватност е важно за нас. Поради оваа причина, развивме Политика за приватност која опишува како ги користиме и складираме вашите информации. Ве молиме прегледајте ги нашите практики за приватност и кажете ни ако имате какви било прашања.
Собирање и користење на лични информации
Личните информации се однесуваат на податоци што може да се користат за идентификување или контактирање на одредена личност.
Може да биде побарано од вас да ги дадете вашите лични податоци во секое време кога ќе не контактирате.
Подолу се дадени неколку примери за типовите на лични информации што можеме да ги собираме и како можеме да ги користиме тие информации.
Кои лични податоци ги собираме:
- Кога поднесувате апликација на страницата, може да собереме различни информации, вклучувајќи го вашето име, телефонски број, адреса Е-поштаитн.
Како ги користиме вашите лични податоци:
- Собрани од нас лични податоцини овозможува да ве контактираме и да ве информираме за уникатни понуди, промоции и други настани и претстојни настани.
- Од време на време, може да ги користиме вашите лични податоци за да испраќаме важни известувања и комуникации.
- Може да користиме и лични информации за внатрешни цели, како што се спроведување ревизии, анализа на податоци и разни истражувања со цел да ги подобриме услугите што ги обезбедуваме и да ви дадеме препораки во врска со нашите услуги.
- Ако учествувате во наградно извлекување, натпревар или слична промоција, ние може да ги користиме информациите што ги давате за администрирање на такви програми.
Откривање на информации на трети страни
Ние не ги откриваме информациите добиени од вас на трети страни.
Исклучоци:
- Доколку е потребно - во согласност со закон, судска постапка, правни постапки и/или врз основа на јавни барања или барања од владини агенциина територијата на Руската Федерација - обелоденете ги вашите лични податоци. Ние, исто така, може да откриеме информации за вас ако утврдиме дека таквото откривање е неопходно или соодветно за безбедност, спроведување на законот или други цели од јавна важност.
- Во случај на реорганизација, спојување или продажба, можеме да ги пренесеме личните информации што ги собираме на соодветната трета страна наследник.
Заштита на лични информации
Преземаме мерки на претпазливост - вклучувајќи административни, технички и физички - за да ги заштитиме вашите лични информации од губење, кражба и злоупотреба, како и од неовластен пристап, откривање, менување и уништување.
Почитување на вашата приватност на ниво на компанија
За да се осигураме дека вашите лични информации се безбедни, ние ги пренесуваме стандардите за приватност и безбедност на нашите вработени и строго ги спроведуваме практиките за приватност.
За успешно да ја користите операцијата за вадење корен во пракса, треба да се запознаете со својствата на оваа операција.
Сите својства се формулирани и докажани само за не-негативни вредности на променливите содржани под знаците на корените.
Теорема 1. n-ти коренмоќи (n=2, 3, 4,...) од производот на два ненегативни чипови е еднаков на производот n-ти коренимоќите на овие броеви:
Коментар:
1.
Теоремата 1 останува валидна за случајот кога радикалниот израз е производ на повеќе од два ненегативни броја.
Теорема 2.Ако,
и n е природен број поголем од 1, тогаш еднаквоста е точно
Кратко(иако неточна) формулација, која е попогодна за употреба во пракса: коренот на фракцијата е еднаков на фракцијата на корените.
Теорема 1 ни овозможува да множиме t само корени од ист степен
, т.е. само корени со ист индекс.
Теорема 3.Ако ,k е природен број, а n е природен број поголем од 1, тогаш еднаквоста е точно
Со други зборови, за да се подигне корен на природна моќ, доволно е да се подигне радикалниот израз на оваа моќ.
Ова е последица на теоремата 1. Всушност, на пример, за k = 3 добиваме: Можеме да расудуваме на ист начин во случај на која било друга природна вредност на експонентот k.
Теорема 4.Ако ,k, n се природни броеви поголеми од 1, тогаш еднаквоста е точно
Со други зборови, за да се извлече корен од корен, доволно е да се умножат индикаторите на корените.
На пример,
Внимавај!Научивме дека на корените може да се извршат четири операции: множење, делење, степенување и вадење корен (од коренот). Но, што е со собирањето и одземањето на корените? Нема шанси.
На пример, наместо да пишувате Навистина, но очигледно е дека
Теорема 5.Ако индикаторите на коренот и радикалниот израз се множат или делат со ист природен број, тогаш вредноста на коренот нема да се промени, т.е.
Примери за решавање проблеми
Пример 1.Пресметај
Решение.Користејќи го првото својство на корените (теорема 1), добиваме:
Пример 2.Пресметај
Решение.Претворете мешан број во неправилна дропка.
Имаме Користење на второто својство на корените ( Теорема 2
), добиваме:
![]()
Пример 3.Пресметајте: ![]()
Решение.Секоја формула во алгебрата, како што добро знаете, се користи не само „од лево кон десно“, туку и „од десно кон лево“. Така, првото својство на корените значи дека тие можат да бидат претставени во форма и, обратно, да се заменат со изразот. Истото важи и за второто својство на корените. Земајќи го ова предвид, ајде да ги извршиме пресметките.
Час и презентација на тема: „Својства на n-тиот корен. Теореми“
Дополнителни материјали
Почитувани корисници, не заборавајте да ги оставите вашите коментари, критики, желби! Сите материјали се проверени со антивирусна програма.
Наставни средства и симулатори во онлајн продавницата Integral за 11 одделение
Интерактивен прирачник за 9-11 одделение „Тригонометрија“
Интерактивен прирачник за 10-11 одделение „Логаритми“
Својства на n-тиот корен. Теореми
Момци, продолжуваме да ги проучуваме n-тите корени на реален број. Како и скоро сите математички предмети, корените од n-ти степен имаат одредени својства, денес ќе ги проучуваме.Сите својства што ќе ги разгледаме се формулирани и докажани само за ненегативни вредности на променливите содржани под знакот на коренот.
Во случај на непарен корен експонент, тие се изведуваат и за негативни променливи.
Теорема 1. n-тиот корен од производот на два ненегативни броја е еднаков на производот од n-тиот корен на овие броеви: $\sqrt[n](a*b)=\sqrt[n](a)*\ sqrt[n](b)$.
Ајде да ја докажеме теоремата.
Доказ. Момци, за да ја докажеме теоремата, да воведеме нови променливи, да ги означиме:
$\sqrt[n](a*b)=x$.
$\sqrt[n](a)=y$.
$\sqrt[n](b)=z$.
Треба да докажеме дека $x=y*z$.
Имајте предвид дека важат и следните идентитети:
$a*b=x^n$.
$a=y^n$.
$b=z^n$.
Тогаш важи следниот идентитет: $x^n=y^n*z^n=(y*z)^n$.
Силите на два ненегативни броја и нивните експоненти се еднакви, тогаш основите на самите сили се еднакви. Ова значи $x=y*z$, што требаше да се докаже.
Теорема 2. Ако $a≥0$, $b>0$ и n е природен број поголем од 1, тогаш важи следната еднаквост: $\sqrt[n](\frac(a)(b))=\frac(\sqrt [ n](а))(\sqrt[n](b))$.
Односно, n-тиот корен од количникот е еднаков на количникот на n-тиот корен.
Доказ.
За да го докажеме ова, ќе користиме поедноставен дијаграм во форма на табела:
Примери за пресметување на n-тиот корен
Пример.Пресметајте: $\sqrt(16*81*256)$.
Решение. Да ја користиме теорема 1: $\sqrt(16*81*256)=\sqrt(16)*\sqrt(81)*\sqrt(256)=2*3*4=24$.
Пример.
Пресметајте: $\sqrt(7\frac(19)(32))$.
Решение. Да го претставиме радикалниот израз во форма неправилна дропка: $7\frac(19)(32)=\frac(7*32+19)(32)=\frac(243)(32)$.
Да ја користиме теорема 2: $\sqrt(\frac(243)(32))=\frac(\sqrt(243))(\sqrt(32))=\frac(3)(2)=1\frac(1 ) (2) $.
Пример.
Пресметајте:
а) $\sqrt(24)*\sqrt(54)$.
б) $\frac(\sqrt(256))(\sqrt(4))$.
Решение:
а) $\sqrt(24)*\sqrt(54)=\sqrt(24*54)=\sqrt(8*3*2*27)=\sqrt(16*81)=\sqrt(16)*\ sqrt(81)=2*3=6$.
б) $\frac(\sqrt(256))(\sqrt(4))=\sqrt(\frac(256)(4))=\sqrt(64)=24$.
Теорема 3. Ако $a≥0$, k и n се природни броеви поголеми од 1, тогаш важи еднаквоста: $(\sqrt[n](a))^k=\sqrt[n](a^k)$.
За да се подигне коренот на природна моќ, доволно е да се подигне радикалниот израз на оваа моќ.
Доказ.
ајде да размислиме посебен случајза $k=3$. Да ја искористиме теоремата 1.
$(\sqrt[n](a))^k=\sqrt[n](a)*\sqrt[n](a)*\sqrt[n](a)=\sqrt[n](a*a *a)=\sqrt[n](a^3)$.
Истото може да се докаже и за секој друг случај. Дечки, докажете сами за случајот кога $k=4$ и $k=6$.
Теорема 4. Ако $a≥0$ b n,k се природни броеви поголеми од 1, тогаш важи еднаквоста: $\sqrt[n](\sqrt[k](a))=\sqrt(a)$.
За да се извлече корен од корен, доволно е да се умножат индикаторите на корените.
Доказ.
Ајде повторно накратко да го докажеме со помош на табела. За да го докажеме ова, ќе користиме поедноставен дијаграм во форма на табела: 
Пример.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.
$\sqrt(\sqrt(a))=\sqrt(a)$.
Теорема 5. Ако експонентите на коренот и радикалниот израз се помножат со ист природен број, тогаш вредноста на коренот нема да се промени: $\sqrt(a^(kp))=\sqrt[n](a)$ .
Доказ.
Принципот на докажување на нашата теорема е ист како и во другите примери. Ајде да воведеме нови променливи:
$\sqrt(a^(k*p))=x=>a^(k*p)=x^(n*p)$ (по дефиниција).
$\sqrt[n](a^k)=y=>y^n=a^k$ (по дефиниција).
Да ја подигнеме последната еднаквост на моќта стр
$(y^n)^p=y^(n*p)=(a^k)^p=a^(k*p)$.
Добив:
$y^(n*p)=a^(k*p)=x^(n*p)=>x=y$.
Односно $\sqrt(a^(k*p))=\sqrt[n](a^k)$, што требаше да се докаже.
Примери:
$\sqrt(a^5)=\sqrt(a)$ (ги подели индикаторите со 5).
$\sqrt(a^(22))=\sqrt(a^(11))$ (ги подели индикаторите со 2).
$\sqrt(a^4)=\sqrt(a^(12))$ (индикатори помножени со 3).
Пример.
Изведете дејства: $\sqrt(a)*\sqrt(a)$.
Решение.
Експонентите на корените се различни броеви, така што не можеме да ја користиме теорема 1, но со примена на теорема 5, можеме да добиеме еднакви експоненти.
$\sqrt(a)=\sqrt(a^3)$ (индикатори помножени со 3).
$\sqrt(a)=\sqrt(a^4)$ (индикатори помножени со 4).
$\sqrt(a)*\sqrt(a)=\sqrt(a^3)*\sqrt(a^4)=\sqrt(a^3*a^4)=\sqrt(a^7)$.
Проблеми кои треба да се решаваат самостојно
1. Пресметајте: $\sqrt(32*243*1024)$.2. Пресметајте: $\sqrt(7\frac(58)(81))$.
3. Пресметајте:
а) $\sqrt(81)*\sqrt(72)$.
б) $\frac(\sqrt(1215))(\sqrt(5))$.
4. Поедностави:
а) $\sqrt(\sqrt(a))$.
б) $\sqrt(\sqrt(a))$.
в) $\sqrt(\sqrt(a))$.
5. Изведете дејства: $\sqrt(a^2)*\sqrt(a^4)$.