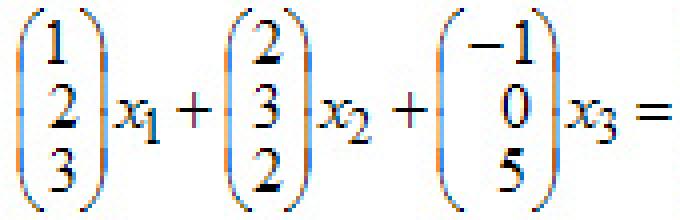Изразување на формата повикани линеарна комбинација на вектори A 1 , A 2 ,...,A nсо коефициенти λ 1, λ 2 ,..., λ n.

Определување на линеарна зависност на систем од вектори

Векторски систем A 1 , A 2 ,...,A nповикани линеарно зависни, ако има ненула множество броеви λ 1, λ 2 ,..., λ n, во која линеарната комбинација на вектори λ 1 *A 1 +λ 2 *A 2 +...+λ n *A nеднаков на векторот нула, односно системот на равенки: има решение кое не е нула.
Збир на броеви λ 1, λ 2 ,..., λ n е ненула ако барем еден од броевите λ 1, λ 2 ,..., λ n различен од нула.

Определување на линеарна независност на систем на вектори

Векторски систем A 1 , A 2 ,...,A nповикани линеарно независни, ако линеарната комбинација на овие вектори λ 1 *A 1 +λ 2 *A 2 +...+λ n *A nеднаков на нултиот вектор само за нулта група броеви λ 1, λ 2 ,..., λ n , односно системот на равенки: A 1 x 1 +A 2 x 2 +...+A n x n =Θима единствено нула решение.

Пример 29.1

Проверете дали системот на вектори е линеарно зависен

Решение:

1. Составуваме систем на равенки:

2. Го решаваме со методот на Гаус. Трансформациите на Jordanano на системот се дадени во Табела 29.1. При пресметувањето, десните страни на системот не се запишуваат бидејќи се еднакви на нула и не се менуваат за време на трансформациите на Џордан.

3. Од последните три реда на табелата запишете решен систем еквивалентен на оригиналниотсистем:

4. Го добиваме општото решение на системот:

5. Откако ја поставивте вредноста на слободната променлива x 3 =1 по ваша дискреција, добиваме одредено решение кое не е нула X=(-3,2,1).

Одговор: Така, за ненулта множество броеви (-3,2,1), линеарната комбинација на вектори е еднаква на нултиот вектор -3A 1 +2A 2 +1A 3 =Θ. Оттука, векторски систем линеарно зависен.

Својства на векторските системи

Имотот (1)
Ако системот на вектори е линеарно зависен, тогаш барем еден од векторите е проширен во однос на другите и, обратно, ако барем еден од векторите на системот е проширен во однос на другите, тогаш системот на вектори е линеарно зависен.

Имотот (2)
Ако некој потсистем на вектори е линеарно зависен, тогаш целиот систем е линеарно зависен.

Имотот (3)
Ако системот на вектори е линеарно независен, тогаш кој било од неговите потсистеми е линеарно независен.

Имотот (4)
Секој систем на вектори што содржи нулта вектор е линеарно зависен.

Имотот (5)
Систем од m-димензионални вектори е секогаш линеарно зависен ако бројот на вектори n е поголем од нивната димензија (n>m)

Основа на векторскиот систем

Основата на векторскиот систем A 1 , A 2 ,..., A n таков потсистем B 1 , B 2 ,...,B r се вика(секој од векторите B 1, B 2,..., B r е еден од векторите A 1, A 2,..., A n), кој ги задоволува следните услови:
1. Б 1 , Б 2 ,..., Б рлинеарно независен систем на вектори;
2. кој било векторА ј систем A 1 , A 2 ,..., A n линеарно се изразува преку векторите B 1 , B 2 ,..., B r

р— бројот на вектори вклучени во основата.

Теорема 29.1 На единична основа на систем од вектори.

Ако системот од m-димензионални вектори содржи m различни единечни вектори E 1 E 2 ,..., E m , тогаш тие ја формираат основата на системот.

Алгоритам за наоѓање на основа на систем од вектори

За да се најде основата на системот на вектори A 1 ,A 2 ,...,A n потребно е:

  • Создадете хомоген систем на равенки што одговара на системот на вектори A 1 x 1 +A 2 x 2 +...+A n x n =Θ
  • Донесете го овој систем

Вектори, нивните својства и дејства со нив

Вектори, дејства со вектори, линеарен векторски простор.

Векторите се подредена збирка од конечен број реални броеви.

Дејства: 1.Множење на вектор со број: ламбда*вектор x=(ламда*х 1, ламбда*х 2 ... ламбда*х n).(3.4, 0, 7)*3=(9, 12,0.21)

2. Собирање вектори (припаѓаат на истиот векторски простор) вектор x + вектор y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Вектор 0=(0,0…0)---n E n – n-димензионален (линеарен простор) вектор x + вектор 0 = вектор x

Теорема. За да може системот од n вектори, n-димензионален линеарен простор, да биде линеарно зависен, потребно е и доволно еден од векторите да биде линеарна комбинација на другите.

Теорема. Секое множество од n+ 1 вектори на n-димензионален линеарен простор на појави. линеарно зависни.

Собирање вектори, множење на вектори со броеви. Одземање на вектори.

Збирот на два вектори е вектор насочен од почетокот на векторот до крајот на векторот, под услов почетокот да се совпаѓа со крајот на векторот. Ако векторите се дадени со нивните проширувања во вектори на базични единици, тогаш кога се собираат вектори, се додаваат нивните соодветни координати.

Да го разгледаме ова користејќи го примерот на Декартов координатен систем. Нека

Да го покажеме тоа

Од Слика 3 е јасно дека

Збирот на кој било конечен број вектори може да се најде со користење на правилото многуаголник (сл. 4): за да се конструира збир на конечен број вектори, доволно е да се комбинира почетокот на секој следен вектор со крајот на претходниот и конструирај вектор кој го поврзува почетокот на првиот вектор со крајот на последниот.

Својства на операцијата за собирање вектор:

Во овие изрази m, n се броеви.

Разликата меѓу векторите се нарекува вектор.Вториот член е вектор спротивен на векторот во насока, но еднаков на него по должина.

Така, операцијата на одземање вектори се заменува со операција за собирање

Вектор чиј почеток е на почетокот и на крајот во точката A (x1, y1, z1) се нарекува вектор на радиус на точката A и се означува едноставно. Бидејќи неговите координати се совпаѓаат со координатите на точката А, нејзиното проширување во единечни вектори има форма

Вектор кој започнува во точката A(x1, y1, z1) и завршува во точка B(x2, y2, z2) може да се запише како

каде што r 2 е векторот на радиусот на точката B; r 1 - вектор на радиус на точката А.

Според тоа, проширувањето на векторот во единечни вектори има форма

Неговата должина е еднаква на растојанието помеѓу точките А и Б

МНОЖЕЊЕ

Значи, во случај на проблем со рамнина, производот на вектор со a = (ax; ay) со бројот b се наоѓа со формулата

a b = (ax b; ay b)

Пример 1. Најдете го производот на векторот a = (1; 2) на 3.

3 a = (3 1; 3 2) = (3; 6)

Значи, во случај на просторен проблем, производот на векторот a = (ax; ay; az) со бројот b се наоѓа со формулата

a b = (ax b; ay b; az b)

Пример 1. Најдете го производот на векторот a = (1; 2; -5) на 2.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Точка производ на вектори и каде е аголот помеѓу векторите и ; ако било, тогаш

Од дефиницијата на скаларниот производ произлегува дека

каде што, на пример, е големината на проекцијата на векторот на насоката на векторот.

Скаларен квадрат вектор:

Својства на производот со точки:

Точка производ во координати

Ако Тоа

Агол помеѓу вектори

Агол помеѓу вектори - аголот помеѓу насоките на овие вектори (најмал агол).

вкрстен производ (Вкрстен производ на два вектори.) -ова е псевдовектор нормално на рамнина изградена од два фактора, што е резултат на бинарната операција „векторско множење“ над вектори во тродимензионалниот Евклидов простор. Производот не е ниту комутативен ниту асоцијативен (тој е антикомутативен) и се разликува од точкастиот производ на вектори. Во многу инженерски и физички проблеми, треба да можете да конструирате вектор нормален на два постоечки - векторскиот производ ја дава оваа можност. Вкрстениот производ е корисен за „мерење“ на нормалноста на векторите - должината на вкрстениот производ на два вектори е еднаква на производот од нивните должини ако се нормални, а се намалува на нула ако векторите се паралелни или антипаралелни.

Вкрстениот производ е дефиниран само во тридимензионални и седумдимензионални простори. Резултатот од векторски производ, како скаларен производ, зависи од метриката на Евклидовиот простор.

За разлика од формулата за пресметување вектори на скаларен производ од координати во тридимензионален правоаголен координатен систем, формулата за вкрстениот производ зависи од ориентацијата на правоаголниот координатен систем или, со други зборови, неговата „хиралност“

Колинеарност на вектори.

Два вектори без нула (не еднакви на 0) се нарекуваат колинеарни ако лежат на паралелни прави или на иста права. Прифатлив, но не и препорачан синоним е „паралелните“ вектори. Колинеарните вектори можат да бидат идентично насочени („конасочни“) или спротивно насочени (во вториот случај понекогаш се нарекуваат „антиколинеарни“ или „антипаралелни“).

Мешан производ на вектори( а, б, в)- скаларен производ на векторот a и векторскиот производ на векторите b и c:

(a,b,c)=a ⋅(b ×c)

понекогаш се нарекува производ со тројна точка на вектори, очигледно затоа што резултатот е скалар (поточно, псевдоскалар).

Геометриско значење: Модулот на мешаниот производ е нумерички еднаков на волуменот на паралелепипедот формиран од векторите (а, б, в) .

Својства

Мешаниот производ е кос-симетричен во однос на сите негови аргументи: т.е. д. преуредувањето на кои било два фактори го менува знакот на производот. Следи дека мешаниот производ во десниот Декартов координатен систем (во ортонормална основа) е еднаков на детерминантата на матрицата составена од вектори и:

Мешаниот производ во левиот Декартов координатен систем (во ортонормална основа) е еднаков на детерминантата на матрицата составена од вектори и земена со знак минус:

Особено,

Ако било кои два вектори се паралелни, тогаш со кој било трет вектор тие формираат мешан производ еднаков на нула.

Ако три вектори се линеарно зависни (односно, компланарни, лежат во иста рамнина), тогаш нивниот измешан производ е еднаков на нула.

Геометриско значење - Мешаниот производ е еднаков по апсолутна вредност на волуменот на паралелепипедот (види слика) формиран од векторите и; знакот зависи од тоа дали оваа тројка вектори е деснак или левак.

Копланарност на вектори.

Три вектори (или повеќе) се нарекуваат компланарни ако тие, сведени на заедничко потекло, лежат во иста рамнина

Својства на компланарност

Ако барем еден од трите вектори е нула, тогаш и трите вектори се сметаат за компланарни.

Тројката вектори што содржи пар колинеарни вектори е компланарна.

Мешан производ на компланарни вектори. Ова е критериум за компланарност на три вектори.

Копланарните вектори се линеарно зависни. Ова е исто така критериум за компланарност.

Во 3-димензионалниот простор, 3 некомпланарни вектори формираат основа

Линеарно зависни и линеарно независни вектори.

Линеарно зависни и независни векторски системи.Дефиниција. Векторскиот систем се нарекува линеарно зависни, ако има барем една нетривијална линеарна комбинација од овие вектори еднаква на нултиот вектор. Во спротивно, т.е. ако само тривијална линеарна комбинација од дадени вектори е еднаква на нултиот вектор, векторите се нарекуваат линеарно независни.

Теорема (критериум за линеарна зависност). За да може системот на вектори во линеарен простор да биде линеарно зависен, потребно е и доволно барем еден од овие вектори да биде линеарна комбинација на другите.

1) Ако меѓу векторите има барем еден нула вектор, тогаш целиот систем на вектори е линеарно зависен.

Всушност, ако, на пример, , тогаш, под претпоставка, имаме нетривијална линеарна комбинација .▲

2) Ако меѓу векторите некои формираат линеарно зависен систем, тогаш целиот систем е линеарно зависен.

Навистина, нека векторите , , се линеарно зависни. Ова значи дека постои нетривијална линеарна комбинација еднаква на нула вектор. Но, тогаш, под претпоставка , добиваме и нетривијална линеарна комбинација еднаква на нула вектор.

2. Основа и димензија. Дефиниција. Систем на линеарно независни вектори се нарекува векторски простор основана овој простор ако некој вектор од може да се претстави како линеарна комбинација на вектори на овој систем, т.е. за секој вектор има реални броеви таква што важи еднаквоста.Оваа еднаквост се нарекува векторско распаѓањеспоред основата и бројките се нарекуваат координати на векторот во однос на основата(или во основата) .

Теорема (за единственоста на проширувањето во однос на основата). Секој вектор во просторот може да се прошири во основа на единствениот начин, т.е. координати на секој вектор во основата се одредуваат недвосмислено.

Во оваа статија ќе покриеме:

  • што се колинеарни вектори;
  • кои се условите за колинеарност на вектори;
  • кои својства на колинеарни вектори постојат;
  • колкава е линеарната зависност на колинеарните вектори.
Дефиниција 1

Колинеарни вектори се вектори кои се паралелни на една права или лежат на една права.

Пример 1

Услови за колинеарност на вектори

Два вектори се колинеарни ако некој од следниве услови е точно:

  • состојба 1 . Векторите a и b се колинеарни ако има број λ таков што a = λ b;
  • состојба 2 . Векторите a и b се колинеарни со еднакви координатни соодноси:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

  • состојба 3 . Векторите a и b се колинеарни под услов вкрстениот производ и нултиот вектор да се еднакви:

a ∥ b ⇔ a, b = 0

Забелешка 1

Состојба 2 не е применливо ако една од векторските координати е нула.

Забелешка 2

Состојба 3 се однесува само на оние вектори кои се наведени во просторот.

Примери на проблеми за проучување на колинеарноста на векторите

Пример 1

Ги испитуваме векторите a = (1; 3) и b = (2; 1) за колинеарност.

Како да се реши?

Во овој случај, неопходно е да се користи втората состојба на колинеарност. За дадените вектори изгледа вака:

Еднаквоста е лажна. Од ова можеме да заклучиме дека векторите a и b се неколинеарни.

Одговори : a | | б

Пример 2

Која вредност m на векторот a = (1; 2) и b = (- 1; m) е неопходна за векторите да бидат колинеарни?

Како да се реши?

Користејќи го вториот услов за колинеарност, векторите ќе бидат колинеарни ако нивните координати се пропорционални:

Ова покажува дека m = - 2.

Одговор: m = - 2 .

Критериуми за линеарна зависност и линеарна независност на векторските системи

Теорема

Систем на вектори во векторски простор е линеарно зависен само ако еден од векторите на системот може да се изрази во однос на преостанатите вектори од овој систем.

Доказ

Нека системот e 1 , e 2 , . . . , e n е линеарно зависен. Дозволете ни да напишеме линеарна комбинација на овој систем еднаква на нултиот вектор:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

во кои барем еден од комбинациските коефициенти не е еднаков на нула.

Нека k ≠ 0 k ∈ 1 , 2 , . . . , n.

Ние ги делиме двете страни на еднаквоста со коефициент кој не е нула:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

Да означиме:

A k - 1 a m , каде што m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

Во овој случај:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + β n e n = 0

или e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

Следи дека еден од векторите на системот се изразува преку сите други вектори на системот. Што требаше да се докаже (и сл.).

Адекватност

Нека еден од векторите е линеарно изразен преку сите други вектори на системот:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

Го поместуваме векторот e k на десната страна на оваа еднаквост:

0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

Бидејќи коефициентот на векторот e k е еднаков на - 1 ≠ 0, добиваме нетривијално претставување на нула со систем од вектори e 1, e 2, . . . , e n , а тоа, пак, значи дека овој систем на вектори е линеарно зависен. Што требаше да се докаже (и сл.).

Последица:

  • Систем од вектори е линеарно независен кога ниту еден од неговите вектори не може да се изрази во однос на сите други вектори на системот.
  • Систем на вектори кој содржи нула вектор или два еднакви вектори е линеарно зависен.

Својства на линеарно зависните вектори

  1. За 2- и 3-димензионални вектори е исполнет следниот услов: два линеарно зависни вектори се колинеарни. Два колинеарни вектори се линеарно зависни.
  2. За 3-димензионални вектори, следниов услов е задоволен: три линеарно зависни вектори се компланарни. (3 компланарни вектори се линеарно зависни).
  3. За n-димензионални вектори, следниов услов е задоволен: n + 1 вектори се секогаш линеарно зависни.

Примери за решавање проблеми кои вклучуваат линеарна зависност или линеарна независност на вектори

Пример 3

Да ги провериме векторите a = 3, 4, 5, b = - 3, 0, 5, c = 4, 4, 4, d = 3, 4, 0 за линеарна независност.

Решение. Векторите се линеарно зависни бидејќи димензијата на векторите е помала од бројот на вектори.

Пример 4

Да ги провериме векторите a = 1, 1, 1, b = 1, 2, 0, c = 0, - 1, 1 за линеарна независност.

Решение. Ги наоѓаме вредностите на коефициентите при кои линеарната комбинација ќе биде еднаква на нула вектор:

x 1 a + x 2 b + x 3 c 1 = 0

Векторската равенка ја пишуваме во линеарна форма:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Овој систем го решаваме користејќи го методот Гаус:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

Од втората линија ја одземаме првата, од 3-та - 1-виот:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

Од првата линија ја одземаме втората, на третата ја додаваме втората:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Од решението произлегува дека системот има многу решенија. Ова значи дека постои ненулта комбинација на вредности на такви броеви x 1, x 2, x 3 за кои линеарната комбинација на a, b, c е еднаква на нула вектор. Според тоа, векторите a, b, c се линеарно зависни. ​​​​​​​

Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter

Воведен од нас линеарни операции на векториовозможуваат создавање на различни изрази за векторски величинии да ги трансформирате користејќи ги својствата поставени за овие операции.

Врз основа на дадено множество вектори a 1, ..., a n, можете да креирате израз на формата

каде што a 1, ..., и n се произволни реални броеви. Овој израз се нарекува линеарна комбинација на вектори a 1, ..., a n. Броевите α i, i = 1, n, претставуваат линеарни комбинирани коефициенти. Се нарекува и множество вектори систем на вектори.

Во врска со воведениот концепт за линеарна комбинација на вектори, се наметнува проблемот со опишување на множество вектори што може да се запише како линеарна комбинација на даден систем на вектори a 1, ..., a n. Покрај тоа, постојат природни прашања за условите под кои постои претставување на вектор во форма на линеарна комбинација и за единственоста на таквата репрезентација.

Дефиниција 2.1.Се нарекуваат векторите a 1, ..., и n линеарно зависни, ако има множество коефициенти α 1 , ... , α n такви што

α 1 a 1 + ... + α n а n = 0 (2.2)

а барем еден од овие коефициенти не е нула. Ако наведеното множество коефициенти не постои, тогаш векторите се повикуваат линеарно независни.

Ако α 1 = ... = α n = 0, тогаш, очигледно, α 1 a 1 + ... + α n a n = 0. Имајќи го ова на ум, можеме да го кажеме ова: вектори a 1, ..., и n се линеарно независни ако од еднаквоста (2.2) следи дека сите коефициенти α 1 , ... , α n се еднакви на нула.

Следната теорема објаснува зошто новиот концепт се нарекува термин „зависност“ (или „независност“) и дава едноставен критериум за линеарна зависност.

Теорема 2.1.За векторите a 1, ..., и n, n > 1, да бидат линеарно зависни, потребно е и доволно еден од нив да биде линеарна комбинација на другите.

◄ Неопходност. Да претпоставиме дека векторите a 1, ..., и n се линеарно зависни. Според дефиницијата 2.1 за линеарна зависност, во еднаквоста (2.2) лево има најмалку еден коефициент не-нулта, на пример α 1. Оставајќи го првиот член на левата страна на еднаквоста, го преместуваме остатокот на десната страна, менувајќи ги нивните знаци, како и обично. Поделувајќи ја добиената еднаквост со α 1, добиваме

a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n

тие. претставување на векторот a 1 како линеарна комбинација на преостанатите вектори a 2, ..., a n.

Адекватност. Нека, на пример, првиот вектор a 1 може да се претстави како линеарна комбинација од преостанатите вектори: a 1 = β 2 a 2 + ... + β n a n. Пренесувајќи ги сите членови од десната страна налево, добиваме 1 - β 2 a 2 - ... - β n a n = 0, т.е. линеарна комбинација на вектори a 1, ..., a n со коефициенти α 1 = 1, α 2 = - β 2, ..., α n = - β n, еднаква на нула вектор.Во оваа линеарна комбинација, сите коефициенти не се нула. Според дефиницијата 2.1, векторите a 1, ... и n се линеарно зависни.

Дефиницијата и критериумот за линеарна зависност се формулирани да имплицираат присуство на два или повеќе вектори. Сепак, можеме да зборуваме и за линеарна зависност на еден вектор. За да ја реализирате оваа можност, наместо „векторите се линеарно зависни“, треба да кажете „системот на вектори е линеарно зависен“. Лесно е да се види дека изразот „систем од еден вектор е линеарно зависен“ значи дека овој единечен вектор е нула (во линеарна комбинација има само еден коефициент и не треба да биде еднаков на нула).

Концептот на линеарна зависност има едноставна геометриска интерпретација. Следните три изјави го појаснуваат ова толкување.

Теорема 2.2.Два вектори се линеарно зависни ако и само ако тие колинеарна.

◄ Ако векторите a и b се линеарно зависни, тогаш еден од нив, на пример a, се изразува преку другиот, т.е. a = λb за некој реален број λ. Според дефиницијата 1.7 работивектори по број, векторите a и b се колинеарни.

Нека сега векторите a и b се колинеарни. Ако и двете се нула, тогаш очигледно е дека тие се линеарно зависни, бидејќи секоја нивна линеарна комбинација е еднаква на нултиот вектор. Нека еден од овие вектори не е еднаков на 0, на пример векторот b. Да го означиме со λ односот на векторските должини: λ = |a|/|b|. Колинеарни вектори можат да бидат еднонасочноили спротивно насочени. Во вториот случај, го менуваме знакот на λ. Потоа, проверувајќи ја Дефиницијата 1.7, убедени сме дека a = λb. Според теорема 2.1, векторите a и b се линеарно зависни.

Забелешка 2.1.Во случај на два вектори, земајќи го предвид критериумот на линеарна зависност, докажаната теорема може да се преформулира на следниот начин: два вектори се колинеарни ако и само ако едниот од нив е претставен како производ на другиот со број. Ова е погоден критериум за колинеарност на два вектори.

Теорема 2.3.Три вектори се линеарно зависни ако и само ако тие компланарни.

◄ Ако три вектори a, b, c се линеарно зависни, тогаш, според теорема 2.1, еден од нив, на пример a, е линеарна комбинација на другите: a = βb + γс. Да ги комбинираме потеклото на векторите b и c во точката A. Тогаш векторите βb, γс ќе имаат заедничко потекло во точката A и долж според правилото за паралелограм нивниот збир етие. вектор a ќе биде вектор со потекло А и крај, што е теме на паралелограм изграден на вектори на компоненти. Така, сите вектори лежат во иста рамнина, т.е. компланарни.

Нека векторите a, b, c се компланарни. Ако еден од овие вектори е нула, тогаш очигледно ќе биде линеарна комбинација на другите. Доволно е да се земат сите коефициенти на линеарна комбинација еднакви на нула. Според тоа, можеме да претпоставиме дека сите три вектори не се нула. Компатибилен почнаод овие вектори во заедничка точка O. Нека нивните краеви се точките A, B, C, соодветно (сл. 2.1). Преку точката C повлекуваме прави паралелни на прави кои минуваат низ парови точки O, A и O, B. Означувајќи ги пресечните точки како A" и B", добиваме паралелограм OA"CB", според тоа, OC" = OA" + OB". Вектор OA" и ненултиот вектор a = OA се колинеарни, и затоа првиот од нив може да се добие со множење на вториот со реален број α:OA" = αOA. Слично, OB" = βOB, β ∈ R. Како резултат на тоа, добиваме дека OC" = α OA + βOB, т.е. векторот c е линеарна комбинација на вектори a и b. Според теоремата 2.1, векторите a, b, c се линеарно зависни.

Теорема 2.4.Сите четири вектори се линеарно зависни.

◄ Доказот го изведуваме според истата шема како во теорема 2.3. Размислете за произволни четири вектори a, b, c и d. Ако еден од четирите вектори е нула, или меѓу нив има два колинеарни вектори или три од четирите вектори се компланарни, тогаш овие четири вектори се линеарно зависни. На пример, ако векторите a и b се колинеарни, тогаш можеме да ја направиме нивната линеарна комбинација αa + βb = 0 со коефициенти не-нула, а потоа да ги додадеме преостанатите два вектори на оваа комбинација, земајќи ги нулите како коефициенти. Добиваме линеарна комбинација од четири вектори еднакви на 0, во кои има коефициенти не-нула.

Така, можеме да претпоставиме дека меѓу избраните четири вектори, ниту еден вектори не е нула, ниту два не се колинеарни, ниту три се компланарни. Да ја избереме точката O како нивен заеднички почеток. Тогаш краевите на векторите a, b, c, d ќе бидат неколку точки A, B, C, D (сл. 2.2). Низ точката D повлекуваме три рамнини паралелни со рамнините OBC, OCA, OAB и нека A", B", C" се точките на пресек на овие рамнини со правите OA, OB, OS, соодветно. Добиваме паралелепипед OA" C "B" C" B"DA", а векторите a, b, c лежат на неговите рабови што излегуваат од темето O. Бидејќи четириаголникот OC"DC" е паралелограм, тогаш OD = OC" + OC". За возврат, отсечката OC" е дијагонален паралелограм OA"C"B", така што OC" = OA" + OB" и OD = OA" + OB" + OC" .

Останува да се забележи дека паровите вектори OA ≠ 0 и OA" , OB ≠ 0 и OB" , OC ≠ 0 и OC" се колинеарни и, според тоа, можно е да се изберат коефициентите α, β, γ така што OA" = αOA , OB" = βOB и OC" = γOC. Конечно добиваме OD = αOA + βOB + γOC. Следствено, OD векторот се изразува преку другите три вектори, а сите четири вектори, според теорема 2.1, се линеарно зависни.

Дефиниција 1. Линеарна комбинација на вектори е збирот на производите на овие вектори и скалари
:

Дефиниција 2. Векторски систем
се нарекува линеарно зависен систем ако нивната линеарна комбинација (2.8) исчезне:

и меѓу бројките
има барем еден што е различен од нула.

Дефиниција 3. Вектори
се нарекуваат линеарно независни ако нивната линеарна комбинација (2.8) исчезнува само во случај кога сите броеви.

Од овие дефиниции може да се добијат следните последици.

Заклучок 1. Во линеарно зависен систем на вектори, барем еден вектор може да се изрази како линеарна комбинација на другите.

Доказ. Нека (2.9) е задоволена, а за дефинитивно нека е коефициентот
. Потоа имаме:
. Забележете дека и обратното е точно.

Заклучок 2.Ако системот на вектори
содржи нула вектор, тогаш овој систем е (нужно) линеарно зависен - доказот е очигледен.

Заклучок 3. Ако меѓу nвектори
било кој к(
) векторите се линеарно зависни, тогаш тоа е сè nвекторите се линеарно зависни (ќе го испуштиме доказот).

2 0 . Линеарни комбинации на два, три и четири вектори. Да ги разгледаме прашањата за линеарна зависност и независност на вектори на права линија, рамнина и во простор. Да ги претставиме соодветните теореми.

Теорема 1. За два вектори да бидат линеарно зависни, потребно е и доволно тие да бидат колинеарни.

Потреба. Нека векторите И линеарно зависни. Тоа значи дека нивната линеарна комбинација
=0 и (заради дефинитивно)
. Ова подразбира еднаквост
, и (по дефиниција за множење вектор со број) вектори И колинеарна.

Адекватност. Нека векторите И колинеарна ( ║) (претпоставуваме дека тие се различни од нултиот вектор; во спротивно нивната линеарна зависност е очигледна).

Со теорема (2.7) (види §2.1, точка 2 0) тогаш
такви што
, или
– линеарната комбинација е еднаква на нула, а коефициентот на е еднакво на 1 – вектори И линеарно зависни.

Од оваа теорема произлегува следнава последица.

Последица. Доколку векторите И не се колинеарни, тогаш тие се линеарно независни.

Теорема 2. За три вектори да бидат линеарно зависни, потребно е и доволно тие да бидат компланарни.

Потреба. Нека векторите ,И линеарно зависни. Да покажеме дека се компланарни.

Од дефиницијата за линеарна зависност на вектори следува постоење на броеви
И така што линеарната комбинација
, а во исто време (да бидам конкретен)
. Тогаш од оваа еднаквост можеме да го изразиме векторот :=
, односно векторот еднаква на дијагоналата на паралелограмот конструиран на векторите од десната страна на оваа еднаквост (сл. 2.6). Тоа значи дека векторите ,И легнете во иста рамнина.

Адекватност. Нека векторите ,И компланарни. Да покажеме дека тие се линеарно зависни.

Да го исклучиме случајот на колинеарност на кој било пар вектори (бидејќи тогаш овој пар е линеарно зависен и според заклучокот 3 (види став 1 0) сите три вектори се линеарно зависни). Забележете дека оваа претпоставка исто така го исклучува постоењето на нулта вектор меѓу овие три.

Да преместиме три компланарни вектори во една рамнина и да ги доведеме до заедничко потекло. Преку крајот на векторот цртаат прави паралелни со векторите И ; ги добиваме векторите И (сл. 2.7) - нивното постоење е обезбедено со тоа што векторите И вектори кои не се колинеарни по претпоставка. Следи дека векторот =+. Препишување на оваа еднаквост во форма (–1) ++=0, заклучуваме дека векторите ,И линеарно зависни.

Од докажаната теорема следуваат две последици.

Заклучок 1. Нека И неколинеарни вектори, вектор – произволно, лежи во рамнината дефинирана со векторите И , вектор. Потоа, постојат бројки И такви што

=+. (2.10)

Заклучок 2. Доколку векторите ,И не се компланарни, тогаш тие се линеарно независни.

Теорема 3. Сите четири вектори се линеарно зависни.

Ќе го испуштиме доказот; со некои измени го копира доказот на теорема 2. Да дадеме заклучок од оваа теорема.

Последица. За сите некомпланарни вектори ,,и кој било вектор
И такви што

. (2.11)

Коментар. За вектори во (тродимензионален) простор, концептите на линеарна зависност и независност имаат, како што следува од теоремите 1-3 погоре, едноставно геометриско значење.

Нека има два линеарно зависни вектори И . Во овој случај, еден од нив е линеарна комбинација на втората, односно едноставно се разликува од него со нумерички фактор (на пример,
). Геометриски, тоа значи дека двата вектори се на заедничка линија; можат да имаат исти или спротивни насоки (сл. 2.8 xx).

Ако два вектори се наоѓаат под агол еден до друг (сл. 2.9 xx), тогаш во овој случај е невозможно да се добие еден од нив со множење на другиот со број - таквите вектори се линеарно независни. Затоа, линеарната независност на два вектори И значи дека овие вектори не можат да се постават на една права линија.

Дозволете ни да го дознаеме геометриското значење на линеарната зависност и независноста на три вектори.

Нека векторите ,И се линеарно зависни и нека (да бидеме конкретни) векторот е линеарна комбинација на вектори И , односно се наоѓа во рамнината што ги содржи векторите И . Тоа значи дека векторите ,И легнете во иста рамнина. Вистина е и обратното: ако векторите ,И лежат во иста рамнина, тогаш тие се линеарно зависни.

Така, векторите ,И се линеарно независни ако и само ако не лежат во иста рамнина.

3 0 . Концептот на основа. Еден од најважните концепти во линеарната и векторската алгебра е концептот на основа. Ајде да воведеме неколку дефиниции.

Дефиниција 1. Пар вектори се нарекува подреден ако е наведено кој вектор од овој пар се смета за прв, а кој втор.

Дефиниција 2.Нарачан пар ,неколинеарни вектори се нарекува основа на рамнината дефинирана со дадените вектори.

Теорема 1. Било кој вектор на рамнината може да се претстави како линеарна комбинација на основниот систем на вектори ,:

(2.12)

а оваа репрезентација е единствена.

Доказ. Нека векторите И формираат основа. Потоа било кој вектор може да се претстави во форма
.

За да се докаже уникатноста, претпоставете дека има уште едно распаѓање
. Тогаш имаме = 0, и барем една од разликите е различна од нула. Последново значи дека векторите И линеарно зависна, односно колинеарна; ова е во спротивност со изјавата дека тие претставуваат основа.

Но, тогаш има само распаѓање.

Дефиниција 3. Тројката вектори се нарекува подредена ако е наведено кој вектор се смета за прв, кој за втор, а кој е трет.

Дефиниција 4. Подредена тројка од некомпланарни вектори се нарекува основа во просторот.

Овде важи и теоремата за распаѓање и уникатност.

Теорема 2. Било кој вектор може да се претстави како линеарна комбинација на основниот векторски систем ,,:

(2.13)

и ова претставување е единствено (ќе го испуштиме доказот на теоремата).

Во проширувањата (2.12) и (2.13) количините се нарекуваат векторски координати во дадена основа (поточно, по афини координати).

Со фиксна основа
И
можеш да пишуваш
.

На пример, ако е дадена основата
и дадено е дека
, тогаш тоа значи дека има претстава (разложување)
.

4 0 . Линеарни операции на вектори во координатна форма. Воведувањето на основа овозможува линеарните операции на вектори да се заменат со обични линеарни операции на броеви - координатите на овие вектори.

Нека се даде некоја основа
. Очигледно, специфицирањето на векторските координати во оваа основа целосно го одредува самиот вектор. Важат следните предлози:

а) два вектори
И
се еднакви ако и само ако нивните соодветни координати се еднакви:

б) при множење вектор
по број неговите координати се множат со овој број:

; (2.15)

в) кога се собираат вектори, се додаваат нивните соодветни координати:

Ние ќе ги испуштиме доказите за овие својства; Да докажеме својство б) само како пример. Ние имаме

==

Коментар. Во просторот (во авионот) можете да изберете бесконечно многу основи.

Да дадеме пример за премин од една основа во друга и да воспоставиме односи помеѓу векторските координати во различни бази.

Пример 1. Во основниот систем
дадени се три вектори:
,
И
. Во основа ,,вектор има распаѓање. Најдете векторски координати во основата
.

Решение. Имаме проширувања:
,
,
; оттука,
=
+2
+
= =
, тоа е
во основата
.

Пример 2. Оставете некоја основа
четири вектори се дадени со нивните координати:
,
,
И
.

Откријте дали векторите се формираат
основа; ако одговорот е позитивен, најдете го распаѓањето на векторот врз оваа основа.

Решение. 1) векторите формираат основа ако се линеарно независни. Ајде да направиме линеарна комбинација на вектори
(
) и дознајте на што
И оди на нула:
=0. Ние имаме:

=
+
+
=

Со дефинирање на еднаквоста на векторите во координатна форма, го добиваме следниот систем на (линеарни хомогени алгебарски) равенки:
;
;
, чија детерминанта
=1
, односно системот има (само) тривијално решение
. Ова значи линеарна независност на векторите
и затоа тие претставуваат основа.

2) проширување на векторот врз оваа основа. Ние имаме: =
или во координатна форма.

Одејќи кон еднаквоста на вектори во координатна форма, добиваме систем на линеарни нехомогени алгебарски равенки:
;
;
. Решавајќи го (на пример, користејќи го правилото на Крамер), добиваме:
,
,
И (
)
. Имаме векторско распаѓање во основата
:=.

5 0 . Проекција на вектор на оска. Својства на проекциите.Нека има некоја оска л, односно права линија со избрана насока на неа и нека биде даден некој вектор Дозволете ни да го дефинираме концептот на векторска проекција по оска л.

Дефиниција. Векторска проекција по оска лсе вика производот на модулот на овој вектор и косинус на аголот помеѓу оската ли вектор (сл. 2.10):

. (2.17)

Последица на оваа дефиниција е изјавата дека еднакви вектори имаат еднакви проекции (на иста оска).

Да ги забележиме својствата на проекциите.

1) проекција на збирот на вектори на некоја оска леднаков на збирот на проекциите на членовите на векторите на истата оска:

2) проекцијата на производот на скаларот со вектор е еднаква на производот на овој скалар со проекцијата на векторот на истата оска:

=
. (2.19)

Последица. Проекцијата на линеарна комбинација на вектори на оската е еднаква на линеарната комбинација на нивните проекции:

Ќе ги изоставиме доказите за својствата.

6 0 . Правоаголен Декартов координатен систем во вселената.Разложување на вектор во единечни вектори на оските.Нека се изберат три меѓусебно нормални единечни вектори како основа; воведуваме посебни ознаки за нив
. Со поставување на нивните почетоци во точка О, ќе насочиме по нив (во согласност со ортите
) координатни оски Вол,Оји О z(оската со позитивна насока, потекло и единица должина избрана на неа се нарекува координатна оска).

Дефиниција. Подреден систем од три меѓусебно нормални координатни оски со заедничко потекло и заедничка единица за должина се нарекува правоаголен Декартов координатен систем во просторот.

Оска Вол наречена оска на апсцисата, Ој– ординатна оска uO z – апликатор на оска.

Ајде да се справиме со проширувањето на произволен вектор во однос на основата
. Од теоремата (види §2.2, став 3 0, (2.13)) произлегува дека
може уникатно да се прошири над основата
(тука наместо да се назначуваат координати
употреба
):

. (2.21)

Б (2,21)
есенција (декартови правоаголни) векторски координати . Значењето на Декартовските координати се утврдува со следнава теорема.

Теорема. Декартови правоаголни координати
вектор се проекции на овој вектор соодветно на оската Вол,Оји О z.

Доказ.Да го поставиме векторот до потеклото на координатниот систем – точка О. Тогаш неговиот крај ќе се совпадне со некоја точка
.

Ајде да извлечеме низ поентата
три рамнини паралелни на координатните рамнини Oyz,OxzИ Окси(Сл. 2.11 xx). Потоа добиваме:

. (2.22)

Во (2.22) векторите
И
се нарекуваат векторски компоненти
по оските Вол,Оји О z.

Пушти низ
И соодветно се означени аглите формирани од векторот со орти
. Потоа за компонентите ги добиваме следните формули:

=
=
,
=
=
,
=
=
(2.23)

Од (2.21), (2.22) (2.23) наоѓаме:

=
=
;=
=
;=
=
(2.23)

– координати
вектор има проекции на овој вектор на координатните оски Вол,Оји О zсоодветно.

Коментар. Броеви
се нарекуваат косинуси на насоката на векторот .

Векторски модул (дијагонала на правоаголен паралелепипед) се пресметува со формулата:

. (2.24)

Од формулите (2.23) и (2.24) следува дека косинусите на насоката може да се пресметаат со помош на формулите:

=
;
=
;
=
. (2.25)

Подигнувајќи ги двете страни на секоја од еднаквостите во (2.25) и додавајќи ги левата и десната страна на добиените еднаквости член по член, доаѓаме до формулата:

– ниту три агли не формираат одредена насока во просторот, туку само оние чии косинуси се поврзани со релација (2.26).

7 0 . Вектор на радиус и координати на точка.Одредување на вектор според неговиот почеток и крај. Ајде да воведеме дефиниција.

Дефиниција. Векторот на радиусот (означен ) е векторот што го поврзува потеклото Осо оваа точка (сл. 2.12 xx):

. (2.27)

Секоја точка во просторот одговара на одреден вектор на радиус (и обратно). Така, точките во просторот се претставени во векторската алгебра со нивните вектори на радиус.

Очигледно координатите
поени Мсе проекции на неговиот вектор на радиус
на координатни оски:

(2.28’)

и на тој начин,

(2.28)

– вектор на радиус на точка е вектор чиишто проекции на координатните оски се еднакви на координатите на оваа точка. Ова води до два записи:
И
.

Добиваме формули за пресметување на векторски проекции
според координатите на неговото потекло – точка
а крајот - точка
.

Да ги нацртаме векторите на радиусот
и вектор
(Сл. 2.13). Го добиваме тоа

=
=(2.29)

– проекциите на векторот врз векторите на координатната единица се еднакви на разликите помеѓу соодветните координати на крајот и почетокот на векторот.

8 0 . Некои проблеми кои вклучуваат Декартови координати.

1) услови за колинеарност на вектори . Од теоремата (види §2.1, став 2 0, формула (2.7)) следува дека за колинеарност на вектори И потребно е и доволно за да важи следнава врска: =. Од оваа векторска еднаквост добиваме три еднаквости во координатна форма: што подразбира услов за колинеарност на вектори во координатна форма:

(2.30)

– за колинеарност на вектори И потребно е и доволно нивните соодветни координати да бидат пропорционални.

2) растојание помеѓу точките . Од претставата (2.29) произлегува дека растојанието
помеѓу точките
И
се одредува со формулата

=
=. (2.31)

3) поделба на отсечка во даден сооднос . Нека се даваат поени
И
и став
. Треба да се најде
– координати на точки М (Сл. 2.14).

Од условот за колинеарност на вектори имаме:
, каде
И

. (2.32)

Од (2.32) добиваме во координатна форма:

Од формулите (2.32’) можеме да добиеме формули за пресметување на координатите на средната точка на отсечката
, претпоставувајќи
:

Коментар. Ќе ги броиме сегментите
И
позитивни или негативни во зависност од тоа дали нивната насока се совпаѓа со насоката од самиот почеток
сегмент до крај
, или не се совпаѓа. Потоа, користејќи формули (2.32) – (2.32”), можете да ги најдете координатите на точката што ја дели отсечката
надворешно, односно на тој начин што точката на поделба Ме на продолжение на сегментот
, а не во него. Во исто време, се разбира,
.

4) равенка на сферична површина . Ајде да создадеме равенка за сферична површина - геометриски локус на точки
, на еднакво растојание од некој фиксен центар - точка
. Очигледно е дека во овој случај
и земајќи ја предвид формулата (2.31)

Равенката (2.33) е равенката на саканата сферична површина.