1. Првите два знака за еднаквост на правоаголните триаголници.
За два триаголници да бидат еднакви, доволно е три елементи од еден триаголник да се еднакви со соодветните елементи на другиот триаголник, а овие елементи секако мора да вклучуваат барем една страна.
Бидејќи сите прави агли се еднакви еден на друг, правоаголните триаголници веќе имаат еден еднаков елемент, имено еден прав агол.

Следи дека правоаголните триаголници се складни:
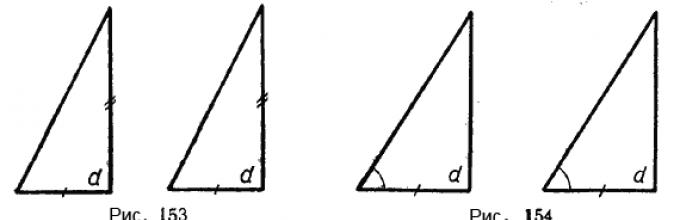
ако катетите на еден триаголник се соодветно еднакви со катетите на друг триаголник (сл. 153);
ако кракот и соседниот остар агол на еден триаголник се соодветно еднакви на кракот и соседниот остар агол на другиот триаголник (Сл. 154).
Сега да докажеме две теореми кои воспоставуваат уште два критериуми за еднаквост на правоаголните триаголници.
Теореми за тестови за еднаквост на правоаголни триаголници
Теорема 1. Ако хипотенузата и акутниот агол на еден триаголник се соодветно еднакви на хипотенузата и акутниот агол на друг триаголник, тогаш таквите правоаголни триаголници се складни.За да ја докажеме оваа теорема, да конструираме два правоаголни агли ABC и A'B'C', во кои аглите A и A' се еднакви, хипотенусите AB и A'B' се исто така еднакви, а аглите C и C' се во право (сл. 157) .

Да го наметнеме триаголникот A’B’C’ на триаголникот ABC така што темето A’ се совпаѓа со темето A, хипотенузата A’B’ се совпаѓа со еднаква хипотенуза AB. Потоа, поради еднаквоста на аглите A и A’, страната A’C’ ќе оди по страната AC; кракот B’C’ ќе се совпадне со кракот BC: и двете се нормални нацртани на една права линија AC од една точка B. Тоа значи дека темињата C и C’ ќе се совпаднат.
Триаголникот ABC се совпаѓа со триаголникот A'B'C'.
Затоа, \(\Delta\)ABC = \(\Delta\)A'B'C'.
Оваа теорема го дава третиот критериум за еднаквост на правоаголните триаголници (по хипотенузата и остриот агол).
Теорема 2. Ако хипотенузата и катетата на еден триаголник се соодветно еднакви со хипотенузата и катетата на друг триаголник, тогаш таквите правоаголни триаголници се складни.
За да го докажеме ова, ајде да конструираме две правоаголни триаголник ABCи A'B'C', во кои аглите C и C' се правилни, катетите AC и A'C' се еднакви, хипотенусите AB и A'B' се исто така еднакви (сл. 158).

Да нацртаме права линија MN и да ја означиме точката C на неа, од оваа точка цртаме нормална SC на права линија MN. Потоа, правиот агол на триаголникот ABC ќе го префрлиме на правиот агол KSM, така што нивните темиња се порамнети и кракот AC оди по зракот SC, а потоа кракот BC оди по зракот CM. Правиот агол на триаголникот A'B'C' ќе биде надреден на правиот агол KCN така што нивните темиња се порамнети и кракот A'C' оди по зракот SK, а потоа кракот C'B' оди по зракот CN. Темињата A и A' ќе се совпаднат поради еднаквоста на краците AC и A'C'.
Триаголниците ABC и A'B'C' ќе се формираат заедно рамнокрак триаголник BAB’, во која AC ќе биде висината и симетралата, а со тоа и оската на симетрија на триаголникот BAB’. Од ова произлегува дека \(\Delta\)ABC = \(\Delta\)A’B’C’.
Оваа теорема го дава четвртиот критериум за еднаквост на правоаголните триаголници (по хипотенуза и крак).
Значи, сите знаци на еднаквост на правоаголните триаголници:
1. Ако две катети од еден правоаголен триаголник се соодветно еднакви на две катети на друг правоаголен триаголник, тогаш таквите правоаголни триаголници се еднакви2. Ако кракот и соседниот остар агол на еден правоаголен триаголник се соодветно еднакви на катетата и соседниот остар агол на друг правоаголен триаголник, тогаш таквите правоаголни триаголници се складни
3. Ако кракот и спротивниот остар агол на еден правоаголен триаголник се соодветно еднакви на катетата и спротивниот остар агол на друг правоаголен триаголник, тогаш таквите правоаголни триаголници се складни
4. Ако хипотенузата и акутниот агол на еден правоаголен триаголник се соодветно еднакви на хипотенузата и акутниот агол на друг правоаголен триаголник, тогаш таквите правоаголни триаголници се складни
5. Ако катетата и хипотенузата на еден правоаголен триаголник се соодветно еднакви на катетата и хипотенузата на друг правоаголен триаголник, тогаш таквите правоаголни триаголници се складни
За да се утврди еднаквоста на правоаголните триаголници, доволно е да се знае дека два елементи од еден триаголник се соодветно еднакви на два елементи од друг триаголник (со исклучок на правиот агол). Ова, се разбира, не важи за еднаквоста на два агли од еден триаголник до два агли на друг триаголник.
Откако во правоаголен триаголникаголот меѓу две катети е права линија, а сите два прави агли се еднакви, тогаш од првиот знак за еднаквост на триаголниците следува:
Ако катетите на еден правоаголен триаголник се соодветно еднакви со катетите на друг, тогаш таквите триаголници се складни (сл. 5).
Ако кракот и соседниот остар агол на еден правоаголен триаголник се соодветно еднакви на кракот и соседниот агол на друг триаголник, тогаш таквите триаголници се складни (сл. 6).

Да разгледаме уште два знака за еднаквост на правоаголните триаголници.

ТЕОРЕМА . Ако хипотенузата и акутниот агол на еден правоаголен триаголник се еднакви на хипотенузата и акутниот агол на друг триаголник, тогаш таквите триаголници се складни (сл. 7).
ДОКАЗ. Од својството 1є § произлегува дека кај таквите триаголници и другите два остри агли се еднакви, па затоа триаголниците се еднакви според вториот знак за еднаквост на триаголниците, односно по страната (хипотенуза) и два соседни агли.
Q.E.D.
ТЕОРЕМА . Ако хипотенузата и катетата на еден правоаголен триаголник се соодветно еднакви на хипотенузата и катетата на друг триаголник, тогаш таквите триаголници се складни.
ДОКАЗ. Ајде да размислиме триаголници ABCи A 1 B 1 C 1 , чии агли C и C 1 се прави агли, AB = A 1 B 1 , BC = B 1 C 1 (сл. 8).

Бидејќи< C = < C 1 , то треугольник ABC можно наложить на треугольник A 1 B 1 C 1 так, что вершина C совместится с вершиной C 1 , а стороны CA и CB наложатся соответственно на лучи C 1 A 1 и C 1 B 1 , поскольку CB = C 1 B 1 , то вершина B совместится с вершиной B 1 . Но тогда вершины A и A 1 также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A 2 луча C 1 A 1 , то получим равнобедренный треугольник A 1 B 1 A 2 , в котором углы при основании A 1 A 2 не равны (на рисунке < A 2 - острый, а < A 1 - тупой как смежный с остар агол B 1 A 1 C 1). Но, ова е невозможно, па темињата A и A 1 ќе се совпаднат. Затоа, триаголниците ABC A 1 B 1 C 1 ќе бидат целосно компатибилни, односно се еднакви.
Q.E.D.
Питагорова теорема
Неговото значење лежи во фактот што повеќето од теоремите на геометријата можат да се извлечат од него или со негова помош. Една од теоремите овозможува да се потврди дека ако кон неа се нацртани нормални и наклонети прави од точка надвор од права, тогаш: а) наклонетите права се еднакви ако нивните проекции се еднакви; б) поголем е оној што е наклонет кој има поголема проекција.
Питагоровата теорема беше првата изјава што ги поврза должините на страните на триаголниците. Потоа научивме како да ги најдеме должините на страните и аглите на акутните и тапи триаголници. Се појави целата наука за тригонометријата („тригон“ значи „триаголник“ на грчки). Оваа наука најде примена во геодетското земјиште. Но, уште порано, со негова помош, тие научија да мерат замислени триаголници на небото, чии темиња беа ѕвезди. Сега тригонометријата се користи дури и за мерење на растојанијата помеѓу вселенските летала.
Користејќи ги својствата на плоштините на многуаголниците, сега ќе воспоставиме извонредна врска помеѓу хипотенузата и катетите на правоаголен триаголник. Теоремата што ќе ја докажеме се нарекува Питагорова теорема, која е најважната теорема во геометријата.
Ако ни се даде триаголник,
И со прав агол на тоа,
Тоа е квадратот на хипотенузата
Секогаш лесно можеме да најдеме:
Ги квачиме нозете,
Го наоѓаме збирот на моќи
И тоа на толку едноставен начин
Ќе дојдеме до резултатот.
ТЕОРЕМА. Во правоаголен триаголник, квадратот на хипотенузата е еднаков на збирот на квадратите на катетите.
ДОКАЗ. Размислете за правоаголен триаголник со катети a, b и c (сл. 9 a).

Да докажеме дека c 2 = a 2 + b 2 . Да го изградиме триаголникот на квадрат со страна a+b, како што е прикажано на сликата (сл. 9 б).
Површината на таков квадрат со страна a + b е еднаква на (a + b) 2. Од друга страна, овој квадрат е составен од четири еднакви правоаголни триаголници со плоштина ab и квадрат со страна c, така што
Така, (a + b) 2 =2ab + c 2, од каде c 2 = a 2 + b 2.
Q.E.D.
КОЛЕРГИЈА 1 . Во правоаголен триаголник, која било од катетите е помала од хипотенузата.
ДОКАЗ. Според Питагоровата теорема AB 2 = AC 2 + BC 2 . Бидејќи BC 2 >0, тогаш AC 2<АВ, То есть АС<АВ.
ЗАКЛУЧОК 2. За секој остар агол b cosb<1.
ДОКАЗ. По дефиниција на косинус cosб = . Но, во заклучокот 1 беше докажано дека АС<АВ, Ова значи дека дропот е помал од 1.
Правоаголните триаголници чии страни се изразуваат како цели броеви се нарекуваат питагорови триаголници.
Може да се докаже дека катетите a, b и хипотенузата c на таквите триаголници се изразени со формулите a=2kmn; b=k(m2-n2); c=k(m 2 +n 2), каде што k, m и n се природни броеви такви што m>n. Триаголниците со страни чии должини се 3, 4, 5 се нарекуваат египетски триаголници, бидејќи им биле познати на старите Египќани.
Разговор со Питагоровата теорема.
Ако квадратот на едната страна на триаголникот е еднаков на збирот на квадратите на другите две страни, тогаш триаголникот е правоаголен (знак за правоаголен триаголник).
ДОКАЗ.
Нека во триаголник ABC AB 2 = AC 2 + BC 2. Да докажеме дека аголот C е прав агол. Размислете за правоаголен триаголник A 1 B 1 C 1 со прав агол C 1, во кој A 1 C 1 = AC и B 1 C 1 = BC. Според Питагоровата теорема A 1 B 1 2 =A 1 C 1 2 +B 1 C 1 2, и затоа A 1 B 1 2 = AC 2 +BC 2. Но, AC 2 + BC 2 = AB 2 според теоремата. Затоа, A 1 B 1 2 = AB 2, од каде A 1 B 1 = AB. Според тоа, триаголниците ABC и A 1 B 1 C 1 се еднакви на три страни< C = < C 1 , то есть треугольник ABC прямоугольный с прямым углом C.
Q.E.D.
Права триаголници, заедно со рамнокраки и рамностран триаголници, го заземаат своето место меѓу триаголниците, поседувајќи посебен сет на специфични својства карактеристични само за овој тип на триаголници. Да разгледаме неколку теореми за еднаквоста на правоаголните триаголници, кои значително ќе го поедностават решавањето на некои проблеми.
Првиот знак за еднаквост на правоаголните триаголници
Знаците за еднаквост на правоаголните триаголници произлегуваат од трите знаци на еднаквост на триаголниците, но правиот агол ги искривува, проширувајќи ги додека ги прави поедноставни. Било кој од знаците за еднаквост на правоаголните триаголници може да се замени со еден од трите главни, но за тоа ќе биде потребно премногу време, па затоа се идентификувани 5 својства и знаци за еднаквост на правоаголните триаголници.
Многу често, наместо да се користат основните знаци на еднаквост на триаголниците, се користи методот на суперпозиција, кога две фигури се ментално надредени една на друга. Не може да се каже дека ова е точно или неточно. Само уште еден метод на докажување што треба да се разгледа. Но, не може да се мисли дека некој знак може да се докаже со обична суперпозиција. Затоа доказот за знаците за еднаквост на правоаголните триаголници ќе го разгледаме преку трите главни знаци за еднаквост на триаголниците.
Првиот знак за еднаквост на правоаголните триаголници вели: два правоаголни триаголници се еднакви ако две катети од еден триаголник се еднакви на две катети на друг триаголник. Накратко, оваа карактеристика се нарекува еднаквост на две страни.

Ориз. 1. Еднаквост на две страни
Докажувањето на овој знак е многу едноставно. Дадено: две катети на правоаголен триаголник се еднакви. Помеѓу краците има прав агол, кој е еднаков на 90 степени, што значи дека аголот на триаголниците се совпаѓа. Според тоа, два триаголници се еднакви во двете страни и аголот меѓу нив.
Втор знак
Вториот знак гласи вака: два правоаголни триаголници се еднакви ако кракот и соседниот остар агол на едниот триаголник се еднакви на кракот и соседниот агол на другиот триаголник.
Вториот знак се докажува врз основа на истата изјава за еднаквоста на правите агли едни со други. Ако триаголниците имаат еднакви катети, нивните остри агли се еднакви, а правите агли се еднакви по дефиниција, тогаш таквите триаголници се еднакви според вториот знак на еднаквост (страна и два соседни агли).
Трет знак
Два правоаголни триаголници се складни ако страната и спротивниот остар агол се еднакви.

Ориз. 2. Цртеж за доказ
Збирот на акутните агли во триаголникот е 90 степени. Да ги означиме аглите со мали латински букви за едноставност на докажувањето. Еден агол е правилен, а другите два се означени со буквите a и b во првиот триаголник; c и d во вториот триаголник.
Аглите a и d се еднакви еден на друг според условите на задачата.
Одземете го аголот a од двете страни на изразот
Односно, ако во два правоаголни триаголници два остри агли се еднакви еден на друг, тогаш и другите два остри агли ќе бидат еднакви, а ние можеме да го користиме вториот знак.
Во вториот и третиот знак, особено треба да се фокусирате на акутниот агол, бидејќи правите агли секогаш се еднакви еден на друг.
Четврти знак
Ако хипотенузата и остриот агол на еден правоаголен триаголник се еднакви на хипотенузата и остриот агол на друг правоаголен триаголник, тогаш триаголниците се складни.
Како што е наведено во претходниот знак: ако остар агол на правоаголен триаголник е еднаков на соодветниот остар агол на друг правоаголен триаголник, тогаш другиот пар остри агли на триаголници ќе бидат еднакви еден на друг.
Тоа значи дека, според условите на овој критериум, имаме еднаквост на хипотенузата и два остри агли на триаголници, што значи дека таквите триаголници ќе бидат еднакви по страните и два соседни агли (втор знак за еднаквост на триаголниците)
Петти знак
Ако хипотенузата и катетата на еден правоаголен триаголник се соодветно еднакви на хипотенузата и катетата на друг триаголник, тогаш таквите триаголници се складни.
Ако хипотенузата и кракот на два триаголници се соодветно еднакви, тогаш вторите катети на таквите триаголници ќе бидат еднакви една со друга. Ова произлегува од Питагоровата теорема.

Ориз. 3. Еднаквост по должината на ногата и хипотенузата
Квадратот на хипотенузата е еднаков на збирот на квадратите на катетите. Хипотенусите се еднакви една со друга, катетата на едниот триаголник е еднаква на квадратот на другиот триаголник, што значи дека збирот останува точен, а другите две кати ќе бидат еднакви една со друга.
Што научивме?
Доказот на петте тестови за еднаквост на триаголници го разгледавме преку основните тестови за еднаквост на триаголници. Сфативме зошто таков доказ е подобар од преклопување и одредивме патека за докажување што ќе ви овозможи да ги вратите основните концепти на темата во меморија во секое време, без непотребно меморирање.
Тест на темата
Рејтинг на статијата
Просечна оцена: 4.6. Вкупно добиени оценки: 100.
Да се потсетиме од материјалот од претходната лекција дека триаголникот се нарекува правоаголен триаголник ако барем еден од неговите агли е прав агол (т.е. еднаков на 90°).
Ајде да размислиме првиот знакРавенство на триаголници: ако две кати од еден правоаголен триаголник се соодветно еднакви на две катети на друг правоаголен триаголник, тогаш таквите триаголници се складни.
Да го илустрираме овој случај:
Ориз. 1. Еднакви правоаголни триаголници
Доказ:
Да се потсетиме на првата еднаквост на произволни триаголници.

Ориз. 2
Ако две страни и аголот меѓу нив на еден триаголник и соодветните две страни и аголот меѓу нив на вториот триаголник се еднакви, тогаш овие триаголници се складни. Ова е означено со првиот знак за еднаквост на триаголниците, односно:

Сличен доказ следи за правоаголните триаголници:
 .
.
Триаголниците се еднакви според првиот критериум.
Да го разгледаме вториот знак за еднаквост на правоаголните триаголници. Ако кракот и соседниот остар агол на еден правоаголен триаголник се соодветно еднакви на кракот и соседниот остар агол на друг правоаголен триаголник, тогаш таквите триаголници се складни.

Ориз. 3
Доказ:

Ориз. 4
Ајде да го искористиме вториот критериум за еднаквост на триаголниците:

Сличен доказ за правоаголни триаголници:

Триаголниците се еднакви според вториот критериум.
Да го разгледаме третиот критериум за еднаквост на правоаголните триаголници: ако хипотенузата и соседниот агол на еден правоаголен триаголник се соодветно еднакви на хипотенузата и соседниот агол на друг триаголник, тогаш таквите триаголници се складни.
Доказ:

Ориз. 5
Да се потсетиме на вториот критериум за еднаквост на триаголниците:

Ориз. 6
Овие триаголници се еднакви ако:

Бидејќи е познато дека еден пар остри агли во правоаголните триаголници е еднаков на (∠A = ∠A 1), тогаш еднаквоста на другиот пар агли (∠B = ∠B 1) се докажува на следниов начин:
Бидејќи AB = A 1 B 1 (по услов), ∠B = ∠B 1, ∠A = ∠A 1. Според тоа, триаголниците ABC и A 1 B 1 C 1 се еднакви според вториот критериум.
Размислете за следниов критериум за еднаквост на триаголниците:
Ако катетата и хипотенузата на еден триаголник се соодветно еднакви на катетата и хипотенузата на друг триаголник, таквите правоаголни триаголници се складни.

Ориз. 7
Доказ:
Да ги споиме триаголниците ABC и A 1 B 1 C 1 со преклопување. Да претпоставиме дека темињата A и A 1, како и C и C 1 се надредени, но темето B и точката B 1 не се совпаѓаат. Токму тоа е случајот прикажан на следната слика:

Ориз. 8
Во овој случај, можеме да го забележиме рамнокрак триаголник ABV 1 (по дефиниција - со условот AB = AB 1). Според тоа, според својството, ∠AB 1 B = ∠ABV 1. Ајде да ја разгледаме дефиницијата за надворешен агол. Надворешен аголна триаголник е аголот во непосредна близина на кој било агол на триаголникот. Неговата мерка на степен е еднаква на збирот на два агли на триаголник кои не се соседни со него. Сликата го покажува овој сооднос:

Ориз. 9
Аголот 5 е надворешниот агол на триаголникот и е еднаков на ∠5 = ∠1 + ∠2. Следи дека надворешен агол е поголем од секој од аглите што не се соседни со него.
Така, ∠ABB 1 е надворешниот агол за триаголникот ABC и е еднаков на збирот ∠ABB 1 = ∠CAB + ∠ACB = ∠ABC = ∠CAB + 90 o. Така, ∠AB 1 B (што е остар агол во правоаголниот триаголник ABC 1) не може да биде еднаков на аголот ∠ABB 1, бидејќи овој агол е тап според докажаното.
Ова значи дека нашата претпоставка за локацијата на точките Б и Б 1 се покажа како неточна, затоа овие точки се совпаѓаат. Тоа значи дека триаголниците ABC и A 1 B 1 C 1 се надредени. Затоа тие се еднакви (по дефиниција).
Така, овие карактеристики не се залудно воведени, бидејќи тие можат да се користат за решавање на некои проблеми.
- Државниот универзитет Омск ().
- Помош порталот calc.ru ().
- Портал за наставници ().
1. Бр 38. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В., уредено од Садовничи В.А. Геометрија 7. М.: Образование. 2010 година
2. Врз основа на податоците наведени на сликата, означете еднакви триаголници, доколку ги има.

3. Врз основа на податоците наведени на сликата, означете еднакви триаголници, доколку ги има. Имајте на ум дека AC = AF.

4. Во правоаголен триаголник, средната и надморската височина се нацртани до хипотенузата. Аголот меѓу нив е 20 o. Одреди ја големината на секој од острите агли на овој правоаголен триаголник.
Секции: Математика
Тема: „Знаци за еднаквост на правоаголните триаголници“
Цел: консолидација на знаењата (својства на правоаголните триаголници), запознавање со некои знаци на еднаквост на правоаголните триаголници.
За време на часовите:
I. Организациски момент.II. Усно.
1. Одговорете на прашањата:
- Именувај ги елементите на правоаголен триаголник.
- Какви својства имаат елементите на правоаголен триаголник?
- Докажете дека кракот на правоаголен триаголник што лежи спроти агол од 30 0 е еднаков на половина од хипотенузата.
- Докажете дека ако катета од правоаголен триаголник е еднаква на половина од хипотенузата, тогаш аголот спроти оваа катета е еднаков на 30 0.
- Најдете x. Изберете го одговорот од триаголникот. Буквите од еден збор се наоѓаат во секторите на триаголникот. Дискусија во парови (3 мин).
Слика 1.
Тие го измислија зборот „знак“.
III. Учење нов материјалСо проучување на триаголниците велиме дека има одредени својства и карактеристики. Кои знаци на еднаквост на триаголниците ги знаете? Ги формулиравме и докажавме својствата на правоаголните триаголници, а денес ќе ги разгледаме знаците на еднаквост на правоаголните триаголници и ќе ги решиме проблемите користејќи ги.
При докажување на еднаквоста на триаголниците, колку парови на соодветно еднакви елементи се пронајдени? Дали е можно да се докаже еднаквоста на правоаголните триаголници долж две страни?
Пред вас се два правоаголни триаголници ABC и A 1 B 1 C 1, нивните краци се соодветно еднакви. Докажете ја, ако е можно, нивната еднаквост.
бр.1. (Од две страни)

Слика 2.
Дадени: ABC и A 1 B 1 C 1, B=B 1 =90 0, AB = A 1 B 1, BC = B 1 C 1
Докажи: ABC = A 1 B 1 C 1
Како ќе звучи знакот? (Потоа задача бр. 1)
бр.2. (Според ногата и акутниот агол во непосредна близина на неа)

Слика 3.
Дадени: ABC и A 1 B 1 C 1, B=B 1 =90 0, BC = B 1 C 1, C= C 1
Докажи: ABC = A 1 B 1 C 1
Како ќе звучи знакот? (Потоа задача бр. 2)
бр. 3. (По хипотенуза и акутен агол)

Слика 4.
Дадени: ABC и A 1 B 1 C 1, B=B 1 =90 0, AC = A 1 C 1, A= A 1
Докажи: ABC = A 1 B 1 C 1
Како ќе звучи знакот? (Потоа задача бр. 3)
Задачи. Најдете складни триаголници и докажете ја нивната еднаквост.

Слика 5.
IV. Зајакнување на наученото во лекцијата.Решете го следниот проблем.

Слика 6.
Дадени: ABC, A 1 B 1 C 1, DAB=CBA=90 0, AD = BD
Докажи: CAB=DBA.
Дискусија во групи од четири (3 мин).
Зошто проблем од учебник бр.261 со снимање.

Слика 7.
Дадени: ABC – рамнокрак, AD и CE – висина на ABC
Докажи: AD = CE
Доказ:
V. Домашна задача.
P.35 (три знаци), бр. 261 (докажи дека AOS е рамнокрак), бр. 268 (тест за еднаквост на правоаголни триаголници долж крак и спротивен агол).
Во следната лекција по геометрија ќе продолжиме со нашето запознавање со знаците на еднаквост на правоаголните триаголници. Ќе давам и оценки следниот пат врз основа на резултатите за 2 лекции.
Дополнително. Најдете еднакви триаголници.