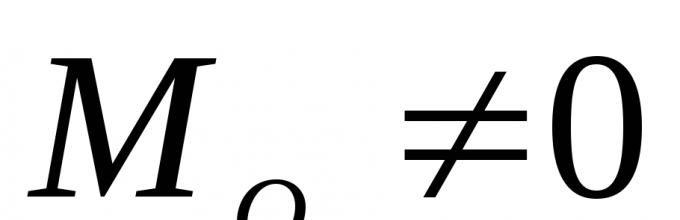Доведување на рамнински систем на сили до дадена точка. Донесување на рамнински систем на сили до центарот. Проверка на исправноста на решението на равенките

Рамен систем на произволно лоцирани сили.

Услови за рамнотежа на парови сили.

Ако на цврсто тело дејствуваат неколку пара сили, произволно лоцирани во просторот, тогаш со последователно применување на правилото паралелограм на секои два моменти од паровите сили, секој број на парови сили може да се замени со еден еквивалентен пар сили. , чиј момент е еднаков на збирот на моментите на дадените парови сили.

Теорема.За рамнотежа на парови сили што се применуваат на цврсто тело, потребно е и доволно алгебарскиот збир на проекциите на моментите на паровите сили на секоја од трите координатни оски да биде еднаков на нула.

Да го разгледаме случајот на пренос на сила во произволна точка што не лежи на линијата на дејство на силата.

Да земеме сила F применета во точката C. Треба да ја пренесеме оваа сила паралелна со себе до одредена точка O. Да примениме во точката O две сили F" и F", спротивно насочени, еднакви по вредност и паралелни на даденото сила F, т.е. F" = F" = F. Примената на овие сили во точката O не ја менува состојбата на телото, бидејќи тие се меѓусебно избалансирани. Добиениот систем од три сили може да се смета дека се состои од сила F" применета во точката O, и пар сили FF" со момент M = Fa. Овој пар на сили се нарекува припоен, а неговиот крак a е еднаков на кракот на силата F во однос на точката O.

Така, кога силата F е доведена до точка што не лежи на линијата на дејство на силата, се добива еквивалентен систем, кој се состои од сила која е иста по големина и насока како силата F, и поврзан пар на сили, чиј момент е еднаков на моментот на дадената сила во однос на фрлените точки:

Како пример за намалување на силата, разгледајте го дејството на силата F на крајот C на стегната прачка (сл. 28б). Откако ќе ја доведеме силата F во точката O на стегната пресек, наоѓаме во неа сила F1 еднаква и паралелна на дадената и приврзан момент M еднаков на моментот на дадената сила F во однос на точката на намалување O,

1.4.2 Доведување на рамнински систем на сили до дадена точка

Опишаниот метод за доведување на една сила до дадена точка може да се примени на кој било број сили. Да претпоставиме дека силите F1, F2, F3, F4 се применуваат во точките на телото A, B, C и D (сл. 30).

Потребно е да се доведат овие сили до точката О на рамнината. Прво да ја претставиме силата F1 применета во точката А. Да примениме во точката O две сили F1" и F1"", паралелни со неа и насочени во спротивни насоки. Како резултат на внесување на сила F1, се добива сила F1" применета во точката О, и пар сили F1 „F1“ со рамо a1 Со тоа што го правиме истото со силата F2 применета во точката B, добиваме сила F2“ применета во точката O, и пар сили со рамо a2 итн.

Рамниот систем на сили применети во точките A, B, C и D го заменивме со конвергирачки сили F1, F2, F3, F4 применети во точката O, и парови сили со моменти еднакви на моментите на дадените сили во однос на точката O :

Силите што се спојуваат во точка може да се заменат со една сила F"hl, еднаква на геометрискиот збир на компонентите,

Оваа сила, еднаква на геометрискиот збир на дадените сили, се нарекува главниот вектор на системот на силии означи F"ch.

Врз основа на правилото за собирање парови сили, тие можат да се заменат со добиениот пар, чиј момент е еднаков на алгебарскиот збир на моментите на дадените сили во однос на точката О и се нарекува главната поентаво однос на референтната точка

Следствено, во општиот случај, рамен систем на сили како резултат на намалување на дадена точка О се заменува со еквивалентен систем кој се состои од една сила (главниот вектор) и еден пар (главниот момент).

Неопходно е да се разбере дека главниот вектор F"ch е резултат на даден систем на сили, бидејќи овој систем не е еквивалентен на една сила F"ch. Само во посебниот случај кога главниот момент ќе исчезне, главниот вектор ќе биде резултат на даден систем на сили. Бидејќи главниот вектор е еднаков на геометрискиот збир на силите на даден систем, ниту неговата големина ниту неговата насока не зависат од изборот на центарот на намалување. Вредноста и знакот на главниот момент Mgl зависат од положбата на центарот на намалување, бидејќи краците на паровите на компонентите зависат од релативната положба на силите и точката (центарот) во однос на која се земаат моментите.

Може да се појават следниве случаи на воведување систем на сили:
1. - општ случај; системот се сведува на главниот вектор и на главниот момент.
2. ; системот се сведува на една резултантна еднаква на главниот вектор на системот.
3. ; системот се сведува на пар сили чиј момент е еднаков на главниот момент.
4. ; системот е во рамнотежа, односно, за рамнотежа на рамномерен систем на сили потребно е и доволно неговиот главен вектор и главен момент да бидат истовремено еднакви на нула.

Може да се докаже дека во општиот случај, кога, секогаш постои точка за која главниот момент на силите е еднаков на нула.

Да разгледаме рамнински систем на сили што е доведен до точката O, односно заменет со главниот вектор применет во точката O и главниот момент. За дефинитивно, претпоставуваме дека главниот момент е насочен во насока на стрелките на часовникот, т.е. Да го претставиме овој главен момент како пар сили FF“, чиј модул ќе биде избран еднаков на модулот на главниот вектор, т.е. ќе примениме една од силите што го сочинуваат парот во центарот на редукција O, другата сила во точката C чија положба ќе се определи од условот: Затоа .

Да подредиме пар сили така што силата F"" е насочена во насока спротивна на главниот вектор F"ch. Во точката O имаме две еднакви меѓусебно спротивни сили F"ch и F"", насочени по истата права линија; може да се отфрлат (според третата аксиома). Следствено, во однос на точката C, главниот момент на системот на сили што се разгледува е еднаков на нула, а системот се сведува на резултатот.

Донесување систем на сили во центарот

Прашања

Предавање 6

3. Услови за рамнотежа за произволен систем на сили

1. Размислете за произволен систем на сили. Ајде да избереме произволна точка ЗАзад центарот на редукција и, користејќи ја теоремата за паралелно пренесување на сила, ги пренесуваме сите сили на системот во дадена точка, не заборавајќи да додадеме поврзан пар сили при пренесување на секоја сила.

Да го замениме системот на конвергирачки сили добиени на овој начин со една сила еднаква на главниот вектор на првобитниот систем на сили. Системот на парови сили формиран за време на преносот ќе биде заменет со еден пар со момент еднаков на геометрискиот збир на моментите на сите парови сили (т.е. геометрискиот збир на моментите на првобитниот систем на сили во однос на центарот ЗА).

Овој момент се нарекува главниот момент на системот на сили во однос на центарот О (Сл. 1.30).

Ориз. 1.30. Донесување систем на сили во центарот

Значи, секој систем на сили секогаш може да се замени со само два фактори на сила - главен вектор и главен момент во однос на произволно избраниот центар на редукција . Очигледно, главниот вектор на системот на сили не зависи од изборот на центарот на редукција (главниот вектор се вели дека е непроменлив во однос на изборот на центарот на редукција). Очигледно е и дека главниот момент го нема ова својство, така што секогаш е неопходно да се означи во однос на кој центар се одредува главниот момент.

2. Доведување на системот на сили во наједноставниот облик

Можноста за дополнително поедноставување на системите на произволна сила зависи од вредноста на нивниот главен вектор и главен момент, како и од успешниот избор на центарот на редукција. Можни се следниве случаи:

а), . Во овој случај, системот се сведува на пар сили со момент, чија вредност не зависи од изборот на центарот на редукција.

б), . Системот се сведува на резултат еднаков на , чија линија на дејство поминува низ центарот ЗА.

в) и се меѓусебно нормални. Системот се сведува на резултат еднаков на, но не поминува низ центарот ЗА(Сл. 1.31).

Ориз. 1.31. Доведување на систем на сили до резултат

Да го замениме главниот момент со пар сили, како што е прикажано на сл. 1.31. Ајде да дефинираме Род условот дека M 0 = R h. Потоа, врз основа на втората аксиома на статиката, да отфрлиме балансиран систем од две сили применети во точка ЗА.

г) и паралелно. Системот се движи со динамична завртка, со оска што минува низ центарот ЗА(Сл. 1.32).

Ориз. 1.32. Динамична завртка

д) и не се еднакви на нула, а во исто време главниот вектор и главниот момент не се паралелни и не се нормални еден на друг. Системот се движи со динамична завртка, но оската не поминува низ центарот ЗА(Сл. 1.33).

Ориз. 1.33. Најопшт случај на намалување на систем на сили

Да претпоставиме дека произволна рамнина систем на сили е намалена на една сила еднаква на главниот вектор и се применува на центарот на намалување, и на еден пар со момент еднаков на главниот момент
(Слика 57, А). Да докажеме дека произволниот систем на сили што се разгледува е намален во овој општ случај на резултантната сила
, чија линија на дејство поминува низ точката А, оддалечен од избраниот центар за редукција ЗАна далечина
. За да го направите ова, ја трансформираме двојката со момент
па таа сила И
, што го сочинува овој пар, се покажа дека е еднаков по големина на главниот вектор R". Во овој случај, потребно е да се избере кракот на парот така што неговиот момент т
остана еднаква на M 0. За ова, потпората на парот
очигледно мора да се најде од еднаквоста

. (1)

Искористувајќи го фактот дека еден пар секогаш може да се помести во неговата рамнина на дејство по желба, дозволете ни да го преместиме парот
така што нејзината сила
се нашол приврзан за адукцискиот центар ЗАа спротивно на главниот вектор
(Слика 57, б).

Според тоа, произволниот систем на сили што се разгледува е еквивалентен на силата
и двојка
. Отфрлање на силите
И
како избалансиран, добиваме дека целиот систем на сили што се разгледува е заменет со една сила
, што е затоа резултатот. Во овој случај, линијата на дејство на резултатот ќе помине низ точката А, чија положба во однос на избраниот центар за редукција се одредува со формулата (1).

Ако, како резултат на доведување на произволна рамнина систем на сили, излезе дека
, А
, тогаш во овој конкретен случај овој систем на сили веднаш се заменува со една сила, т.е. резултантната
, чија линија на дејство поминува низ избраниот центар на редукција.

Проблем 7. До поени ВОИ СОтелата соодветно се применуваат еднакви по големина и меѓусебно нормални сили И
, оддалечен од точката ЗАтела на еднакви растојанија
. Доведете го овој систем на сили до точка ЗА(Слика 58).

Решение. Да ги пренесеме силите И паралелно со самите нас до одреден степен ЗА. Како резултат на таквото пренесување добиваме (слика 58) сили
И
, се применува во точката ЗА, и придружни парови
И
, лежејќи во иста рамнина со моментите
И
(силите што ги формираат овие парови се означени на сликата со 58 цртички). Од геометриско собирање сили И , се применува во точката ЗА, го добиваме главниот вектор на овој систем на сили

чиј модул е ​​очигледно еднаков на

Од собирањето на придружните парови добиваме резултатски пар, чиј момент е еднаков на главниот момент
на даден систем на сили во однос на точка ЗА:

Затоа, овој систем на две сили И има резултат

,

се применува во точката А, што е оддалечено од точката ЗАна далечина

.

;
,

односно резултантните форми со двете дадени сили И еднакви агли од 45 0.

Задача 8.Вертикалните сили дејствуваат на бандажот на мостот (Слика 59)
т и
t соодветно на растојание од 10 ми 40 мод левиот крај на бандажот и хоризонталната сила
т на ниво на горниот акорд на бандажот, висината на бандажот е 6 м. Донесете систем на сили ,И наједноставната форма.

Решение. Ги цртаме координатните оски како што е прикажано на слика 59, земајќи го потеклото на координатите во точката А.Да ги најдеме проекциите на главниот вектор на даден систем на сили на оската на избраниот координатен систем:

каде го наоѓаме модулот на главниот вектор
:

Т
.

Сега да го најдеме главниот момент на дадениот систем на сили во однос на потеклото на координатите А:

т м
.

Следствено, овој систем на сили има резултат
, чиј модул
Т.

Сега да ја најдеме линијата на дејство на резултатот. Резултат на моментот во однос на потеклото Аќе се определи со формулата

,

Каде XИ y - координати на точка што лежи на линијата на дејство на резултантната. Бидејќи
т и
т, тогаш

.

СО од друга страна, со Варињоновата теорема за моментот на резултатот (5, § 11) имаме

Оттука,

.

Ова е равенката на линијата на дејство на резултатот.

Претпоставувајќи во оваа равенка
, откриваме дека точката на пресек на линијата на дејство на резултантната со горниот акорд на бандажот сместен на растојание
мод левиот крај на фармата. Верувајќи
м, откриваме дека точката на пресек на линијата на дејство на резултантната со долниот акорд на бандажот е на растојание
мод левиот крај на фармата. Вака дефинираните врски се точките на пресек на линиите на дејство на резултантот со горните и долните акорди на бандажот во права линија, ја наоѓаме линијата на дејство на резултантната .

Ќе го замениме рамниот систем на сили применети во точките A, B, C, D:

1) сили F 1 “, F 2 “, F 3 “, F 4 “, применети во точката O;

2) во парови сили:

F 1 F 1 ': M 1 = M o (F 1) = F 1 a 1

F 2 F 2 ': M 2 = M o (F 2) = F 2 a 2

F 3 F 3 ': M 3 ​​= M o (F 3) = F 3 a 3

F 4 F 4 ': M 4 = M o (F 4) = F 4 a 4

Силите F 1 ’, F 2 ’, F 3 ’, F 4 ’ што се спојуваат во точката O може да се заменат со една сила (резултант) F ch:

F gl = F 1 ' + F 2 ' + F 3 ' + F 4 ' = F 1 + F 2 + F 3 + F 4

F ch– главниот вектор на системот на сили.

Добиените парови на сили може да се заменат со добиениот пар, чиј момент M ch:

M gl = M 1 + M 2 + M 3 + M 4 = Σ M i = Σ M o (F i)

M gl -главната точка во однос на референтната точка.

Рамниот систем на сили во дадена точка O се заменува со еквивалентен систем кој се состои од една сила (главниот вектор) и еден пар (главниот момент).

Теорема за моментот на резултатот (теорема на Варињон)

Моментот на резултантната рамнина на системот на сили во однос на произволна точка е еднаков на алгебарскиот збир на моментите на силите на компонентите во однос на истата точка.

M o (F Σ)= Σ M o (F i)

Равенки за рамнотежа за рамнински систем на сили

F GL = 0;

M gl = ΣM o (F i) = 0.

Модулот на главниот вектор може да се определи преку проекции на координатните оски на сите сили на системот.

F GL = (ΣF іх) 2 +(ΣF іу) 2 =0 од ова следуваат равенките за рамнотежа:

Σ F іх =0

Σ F іу =0

Σ M o (F i)=0

Други форми на равенки за рамнотежа:

Σ M A (F i)=0

Σ М В (F і)=0 (ABC не лежат на истото

Σ M C (F i)=0 директно)

Σ M A (F i)=0 (оската x не е нормална

Σ M B (F і)=0 директно AB)

Σ F іх =0

За систем на паралелни сили, избирајќи една од проекционите оски паралелни на овие сили (оска y), а другата нормална на нив (оска x), добиваме две рамнотежни равенки:

Σ F іу =0

Σ M o (F i)=0

Σ M A (F i)=0

Σ M V (F i)=0

Алгоритам за решавање проблеми

1. Изберете објект на рамнотежа (тело или точка): ќе ја разгледаме рамнотежата во однос на ...

На сликата ги прикажуваме сите дејствувачки сили, вклучувајќи ги и реакциите на врските.

3. Изберете координатен систем - препорачливо е да ги насочите координатните оски паралелно или нормално на саканите сили.

Составуваме равенки за рамнотежа за предметот на проучување.

Σ F іх =0

Σ F іу =0

Σ M o (F i)=0

Од добиените равенки одредуваме непознати величини (одредуваме реакции).

Ја проверуваме точноста на решението на равенките.

Σ М р (F i)=0

Σ M e (F i)=0

5. Поддржувачки уреди за системи со греди

Артикулирачка поддршка

Форма фиксирана со шарки и цврста заптивка (штипкање)

Тема:

„Центар на гравитација.

Геометриски карактеристики на рамни пресеци“

Планирајте

1. Центар на паралелни сили и неговите координати.
2. Центар на гравитација на области. Статистички моменти на области.
3. Решавање задачи за одредување на координатите на тежиштето на рамна композитна фигура.
4. Поларни и аксијални моменти на инерција.
5. Аксијални моменти на инерција околу паралелните оски.
6. Определување моменти на инерција на композитни пресеци користејќи табели со нормален асортиман.

1. Центар на паралелни сили и неговите координати

Нека е даден систем на паралелни сили F 1, F 2, F 3, ..., Fn; познати се координатите на точките C 1, C2, C3, ..., Cn на примена на овие сили (сл. 42, б). Да ја означиме точката на примена со резултантната буква C, а нејзините координати ги означуваме x c, y c.
FΣ = F 1 + F 2 + F 3+…. + Fn = ΣF i. (1)

FΣ xс = F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn = Σ F i x i,

x c = F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / FΣ = Σ F i x i / FΣ

FΣ = F 1+ F 2+ F 3+…+ Fn= Σ F іх c =
= F 1 x 1 + F 2 x 2 + F 3 x 3 +… + Fnxn / F 1+ F 2+ F 3+…+ Fn= Σ F i x i / F i (2)

Опишаниот метод за доведување на една сила до дадена точка може да се примени на кој било број сили. Да претпоставиме дека во точките на телото А, Б, ЦИ Д(сл. 19) применети сили 1 , 2 , 3 И 4 . Потребно е овие сили да се доведат до точка ЗАавион. Ајде прво да ја дадеме силата 1 , се применува во точката А.Ајде да аплицираме во точката ЗАдве сили ’ 1 И ’’ 1 , секој е еднаков по модул на дадена сила 1 , паралелно со него и насочени во спротивни насоки. Како резултат на доведување на сила 1 ќе ја добиеме моќта ’ 1 , се применува во точката ЗА, и пар сили 1 ’’ 1 (силите што формираат пар се означени со цртички) со рамо а 1. Правејќи го истото со сила 2 , се применува во точката ВО, добиваме сила 2 , се применува во точката ЗА, и пар сили 2 ’’ 2 со рамо а 2итн.

Рамнински систем на сили што се применуваат на точки А, ВО, СОИ Д, го заменивме со конвергирани сили ’ 1 , ’ 2 , ’ 3 И ’ 4 , се применува во точката ЗА, и парови сили со моменти еднакви на моментите на дадените сили во однос на точката ЗА:

M1 = P1 a 1 = M o (1); M 2 = P 2 a 2 = M o (2);

M 3 = – P 3 a 3 = M o ( 3); M 4 = – P 4 a 4 = M o (4).

Силите што се спојуваат во точка може да се заменат со една сила " , еднаква на геометрискиот збир на компонентите,

" = " 1 + " 2 + " 3 + " 4 = 1 + 2 + 3 + 4 = i .(16)

Оваа сила, еднаква на геометрискиот збир на дадените сили, се нарекува главниот вектор на системот на сили.

Врз основа на правилото за собирање парови сили, од може да се замени со добиениот пар, чиј момент е еднаков на алгебарскиот збир на моментите на дадените сили во однос на точката ЗА:

M o = M 1 + M 2 + M 3 + M 4 = i = o (i).(17)

По аналогија со главниот вектор, моментот М 0парови еднакви на алгебарскиот збир на моментите на сите сили во однос на центарот на редукција ЗА, повикан главниот момент на системот во однос на дадениот центар на редукција О.Оттука, во општиот случај, рамен систем на сили како резултат на намалување на дадена точка O се заменува со еквивалентен систем кој се состои од една сила - главниот вектор - и еден пар, чиј момент се нарекува главен момент на даден систем на сили во однос на центарот на редукција.

Неопходно е да се разбере дека главниот вектор ’ не е резултат на даден систем на сили, бидејќи овој систем не е еквивалентен на една сила ’. Само во посебниот случај кога главниот момент ќе исчезне, главниот вектор ќе биде резултат на даден систем на сили. Бидејќи главниот вектор е еднаков на геометрискиот збир на силите на даден систем, ниту неговата големина ниту неговата насока не зависат од изборот на центарот на намалување. Магнитуда и знак на главниот момент М 0зависат од положбата на центарот на редукција, бидејќи краците на паровите на компонентите зависат од релативната положба на силите и точката (центарот) во однос на која се земаат моментите.

Може да се појават следниве случаи на воведување систем на сили:

1. " ≠ 0; M o ≠ 0 -општ случај; системот се сведува на главниот вектор и главниот момент.

2. " ≠ 0; M o = 0;системот се сведува на една резултантна еднаква на главниот вектор на системот.

3. " = 0; M o ≠ 0;системот се сведува на пар сили чиј момент е еднаков на главниот момент.

4. " = 0; M o = 0;системот е во рамнотежа.

Може да се докаже дека во општиот случај кога " ≠ 0 и M o ≠ 0,Секогаш постои точка во однос на која главниот момент на системот на сили е еднаков на нула.

Да разгледаме рамнински систем на сили што е сведена до точка ЗА, т.е. заменет со главен вектор " ≠ 0 , се применува во точката ЗА, и главната поента M o ≠ 0(Сл. 20).

За дефинитивно, претпоставуваме дека главниот момент е насочен во насока на стрелките на часовникот, т.е. М о< 0. Ајде да го отсликаме овој главен момент со пар сили "" , чиј модул е ​​избран еднаков на модулот на главниот вектор " , т.е. Р =R '' = R '. Една од силите што го сочинуваат парот е силата "" – аплицирајте во центарот за намалување ЗА, друга сила – во одреден момент СО, чија положба се одредува од условот: M o = OS*R.Оттука,

ОС =. (18)

Ајде да ставиме неколку сили "" така што силата "" беше насочен во насока спротивна на главниот вектор " . Во точката ЗА(сл. 20) имаме две еднакви и меѓусебно спротивни сили " И "" , насочен по една права линија; може да се отфрлат (според третата аксиома). Затоа, во однос на поентата СОглавниот момент на разгледуваниот систем на сили е еднаков на нула, а системот се сведува на резултатот .

§ 18. Теорема за моментот на резултатот (теорема на Варињон)

Во општиот случај (види § 17), произволниот систем на сили се сведува на главниот вектор " и главната поента М 0во однос на избраниот центар на редукција, а главниот момент е еднаков на алгебарскиот збир на моментите на дадените сили во однос на точката ЗА

M o = o (i).(А)

Се покажа дека е можно да се избере центарот на редукција (на Сл. 20 точката СО), во однос на кој главниот момент на системот ќе биде еднаков на нула, а системот на сили ќе се намали на еден резултат еднаков по големина на главниот вектор ( R = R'). Дозволете ни да го одредиме моментот на резултатот во однос на точката ЗА. Имајќи предвид дека рамото ОСсилите еднакви , добиваме

M o () = R*OC = R = M o.(б)

Две величини, одделно еднакви на третата, се еднакви една на друга, затоа од равенките (а) и (б) наоѓаме

M o () = o (i).(19)

Добиената равенка ја изразува теоремата на Варињон: моментот на резултантната рамнина систем на сили во однос на произволна точка е еднаков на алгебарскиот збир на моментите на составните сили во однос на истата точка.

Од теоремата на Варињон следува дека главниот момент на рамниниот систем на сили во однос на која било точка што лежи на линијата на дејство на неговата резултантна е еднаква на нула.