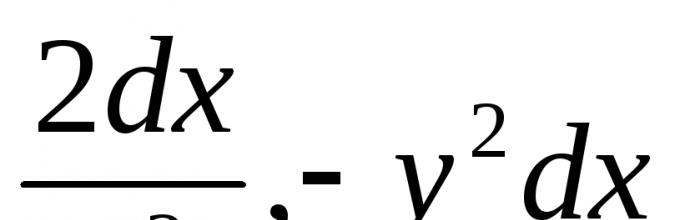Равенката М(x, y) dx+ Н(x, y) ди=0 се нарекува генерализирана хомогена ако е можно да се избере таков број к, дека левата страна на оваа равенка станува хомогена функција од одреден степен м релативно x, y, dx И ди под услов да x се смета за вредноста на првата димензија, y – к‑ ти мерења , dx И ди – соодветно нула и (к-1) ти мерења. На пример, ова би била равенката. (6.1)

Важи според претпоставките направени во врска со мерењата

x, y, dx И ди членови на левата страна
И ди ќе има димензии -2, 2 соодветно кИ к-1. Изедначувајќи ги, добиваме услов што бараниот број мора да го задоволи к: -2 = 2к = к-1. Овој услов е задоволен кога к = -1 (со ова ксите членови од левата страна на равенката што се разгледува ќе имаат димензија -2). Следствено, равенката (6.1) е генерализирана хомогена.

Генерализирана хомогена равенка се сведува на равенка со раздвојливи променливи со помош на замена
, Каде z– нова непозната функција. Дозволете ни да ја интегрираме равенката (6.1) користејќи го наведениот метод. Бидејќи к = -1, тогаш
, по што ја добиваме равенката.

Интегрирајќи го, наоѓаме
, каде
. Ова е општо решение на равенката (6.1).

§ 7. Линеарни диференцијални равенки од 1 ред.

Линеарна равенка од 1-ви ред е равенка која е линеарна во однос на саканата функција и нејзиниот извод. Изгледа како:

, (7.1)

Каде П(x) И П(x) – дадени континуирани функции на x. Доколку функцијата
, тогаш равенката (7.1) има форма:
(7.2)

и се нарекува линеарна хомогена равенка, во спротивно
се нарекува линеарна нехомогена равенка.

Линеарната хомогена диференцијална равенка (7.2) е равенка со раздвојливи променливи:

(7.3)

Изразот (7.3) е општо решение на равенката (7.2). Да се ​​најде општо решение на равенката (7.1), во кое функцијата П(x) ја означува истата функција како во равенката (7.2), применуваме техника наречена метод на варијација на произволна константа и се состои од следново: ќе се обидеме да ја избереме функцијата C=C(x) така што општото решение на линеарната хомогена равенка (7.2) би било решение на нехомогената линеарна равенка (7.1). Потоа за изводот на функцијата (7.3) добиваме:

.

Заменувајќи го пронајдениот извод со равенката (7.1), ќе имаме:

или
.

Каде
, Каде - произволна константа. Како резултат на тоа, општото решение на нехомогената линеарна равенка (7.1) ќе биде (7.4)

Првиот член во оваа формула го претставува општото решение (7.3) на линеарната хомогена диференцијална равенка (7.2), а вториот член од формулата (7.4) е одредено решение на линеарната нехомогена равенка (7.1), добиена од општата ( 7.4) со
. Овој важен заклучок го истакнуваме во форма на теорема.

Теорема.Ако е познато едно одредено решение на линеарна нехомогена диференцијална равенка
, тогаш сите други решенија ја имаат формата
, Каде
- општо решение на соодветната линеарна хомогена диференцијална равенка.

Сепак, треба да се забележи дека за решавање на линеарната нехомогена диференцијална равенка од 1-ви ред (7.1), почесто се користи друг метод, понекогаш наречен Бернули метод. Ќе бараме решение за равенката (7.1) во форма
. Потоа
. Да го замениме пронајдениот извод во првобитната равенка:
.

Да ги комбинираме, на пример, вториот и третиот член од последниот израз и да ја извлечеме функцијата u(x) зад заградата:
(7.5)

Бараме да се поништи заградата:
.

Дозволете ни да ја решиме оваа равенка со поставување на произволна константа В еднакво на нула:
. Со пронајдената функција v(x) Да се ​​вратиме на равенката (7.5):
.

Решавајќи го, добиваме:
.

Следствено, општото решение на равенката (7.1) ја има формата.

деф 1 DU тип

повикани хомогена диференцијална равенка од прв ред(ОДУ).

Ти 1 Нека се исполнети следниве услови за функцијата:

1) континуирано во

Тогаш ODE (1) има општ интеграл, кој е даден со формулата:

каде има некој антидериват на функцијата Сое произволна константа.

Забелешка 1Ако за некои условот е исполнет, тогаш во процесот на решавање на ODE (1) може да се изгубат решенијата од формуларот; таквите случаи мора да се третираат повнимателно и секој од нив да се провери посебно.

Така од теоремата Th1треба да општ алгоритам за решавање на ODE (1):

1) Направете замена:

2) Така, ќе се добие диференцијална равенка со раздвојливи променливи, која треба да се интегрира;

3) Врати се на старите gvariables;

4) Проверете ги вредностите за нивната вклученост во решението оригинален далечински управувач, под кој условот ќе биде исполнет

5) Запишете го одговорот.

Пример 1Решете го DE (4).

Решение: DE (4) е хомогена диференцијална равенка, бидејќи ја има формата (1). Ајде да направиме промена (3), ова ќе ја донесе равенката (4) во форма:

Равенката (5) е генерален интеграл на DE (4).

Забележете дека при одвојување на променливите и делење со, решенијата може да се изгубат, но ова не е решение за DE (4), што лесно се потврдува со директна замена во еднаквост (4), бидејќи оваа вредност не е вклучена во доменот на дефиниција на оригиналниот ДЕ.

Одговор:

Забелешка 2Понекогаш можете да напишете ODE во однос на диференцијали на променливи XИ u.Се препорачува да се префрли од оваа ознака на далечинскиот управувач на изразот преку изводот и дури потоа да се изврши замената (3).

Диференцијални равенки сведени на хомогени.

дефиниција 2 Функцијата се нарекува хомогена функција од степен k во областа, за што ќе биде исполнета еднаквоста:

Еве ги најчестите типови на диференцијални равенки кои може да се редуцираат во форма (1) по различни трансформации.

1) каде е функцијата е хомогена, степен нула, односно, еднаквоста важи: DE (6) лесно се сведува на формата (1), ако ставиме , која понатаму се интегрира со замена (3).

2) (7), каде што функциите се хомогени од ист степен к . DE од формата (7) е исто така интегрирана со помош на замена (3).

Пример 2Решете го DE (8).

Решение:Да покажеме дека DE (8) е хомогена. Дозволете ни да се подели со она што е можно, бидејќи тоа не е решение за DE (8).

Ајде да направиме промена (3), ова ќе ја донесе равенката (9) во форма:

Равенката (10) е генерален интеграл на DE (8).

Забележете дека при одвојување на променливите и делење со, решенијата што одговараат на вредностите на и може да се изгубат. Ајде да ги провериме овие изрази. Ајде да ги замениме во DE (8):



Одговор:

Интересно е да се забележи дека при решавање на овој пример се појавува функција наречена „знак“ на бројот X(чита“ знак x"), дефиниран со изразот:

Забелешка 3Намалувањето на DE (6) или (7) на формата (1) не е потребно; ако е очигледно дека DE е хомогена, тогаш можете веднаш да ја замените

3) DE од формата (11) се интегрира како ODE if, и замената првично се изведува:

(12), каде е решението на системот: (13), а потоа се користи замена (3) за функцијата.По добивањето на општиот интеграл се враќаат на променливите XИ на.

Ако , тогаш, под претпоставка во равенката (11), добиваме диференцијална равенка со раздвојливи променливи.

Пример 3Решете го проблемот со Коши (14).

Решение:Да покажеме дека DE (14) е сведена на хомогена DE и интегрирана според горната шема:

Дозволете ни да го решиме нехомогениот систем на линеарни алгебарски равенки (15) користејќи го Крамеровиот метод:

Ајде да направиме промена на променливите и да ја интегрираме добиената равенка:

(16) – Општ интеграл на ДЕ (14). При раздвојување на променливите, решенијата може да се изгубат при делење со израз, кој може да се добие експлицитно по решавањето на квадратната равенка. Сепак, тие се земени предвид во општиот интеграл (16) на

Ајде да најдеме решение за проблемот Коши: заменете ги вредностите и во општиот интеграл (16) и пронајдете Со.

Така, парцијалниот интеграл ќе биде даден со формулата:

Одговор:

4) Можно е да се редуцираат некои диференцијални равенки на хомогени за нова, сè уште непозната функција ако примениме замена на формата:

Во овој случај бројот мсе избира од условот добиената равенка, ако е можно, да стане хомогена до одреден степен. Меѓутоа, ако тоа не може да се направи, тогаш ДЕ што се разгледува не може на овој начин да се сведе на хомогена.

Пример 4Решете го DE. (18)

Решение:Дозволете ни да покажеме дека DE (18) е сведена на хомогена DE користејќи замена (17) и е дополнително интегрирана со помош на замена (3):

Ајде да најдеме Со:

Така, одредено решение на DE (24) ја има формата

.
Диференцијални равенки.

§ 1. Основни поими за обичните диференцијални равенки.

Дефиниција 1.Обична диференцијална равенка n– редослед за функцијата yаргумент xсе нарекува релација на формата

Каде Ф– дадена функција на неговите аргументи. Во името на оваа класа математички равенки, терминот „диференцијал“ нагласува дека тие вклучуваат деривати
(функции формирани како резултат на диференцијација); терминот „обичен“ означува дека саканата функција зависи само од еден реален аргумент.

Обична диференцијална равенка може да не содржи експлицитен аргумент x, потребната функција
и кој било од неговите деривати, но највисокиот дериват
мора да бидат вклучени во равенката n- ти ред. На пример

А)
– равенка од прв ред;

б)
– равенка од трет ред.

Кога се пишуваат обични диференцијални равенки, често се користи ознаката за деривати во однос на диференцијали:

V)
– равенка од втор ред;

G)
- равенка од прв ред,

генератор по делење со dxеквивалентна форма за одредување на равенката:
.

Функција
се нарекува решение на обична диференцијална равенка ако, при замена во неа, се претвора во идентитет.

На пример, равенка од 3 ред

Има решение
.

Да се ​​најде со еден или друг метод, на пример, избор, една функција што ја задоволува равенката не значи и нејзино решавање. Да се ​​реши обична диференцијална равенка значи да се најде Ситефункции кои формираат идентитет кога се заменуваат во равенка. За равенката (1.1), семејство на такви функции се формира со помош на произволни константи и се нарекува општо решение на обична диференцијална равенка n-ти ред, а бројот на константи се совпаѓа со редот на равенката: Општото решение може да биде, но не е експлицитно решено во однос на y(x) : Во овој случај, решението обично се нарекува општ интеграл на равенката (1.1).

На пример, општото решение на диференцијалната равенка
е следниот израз: , а вториот член може да се запише и како
, бидејќи произволна константа , поделено со 2, може да се замени со нова произволна константа .

Со доделување на некои дозволени вредности на сите произволни константи во општото решение или во општиот интеграл, добиваме одредена функција која повеќе не содржи произволни константи. Оваа функција се нарекува делумно решение или парцијален интеграл на равенката (1.1). За да се пронајдат вредностите на произволните константи, а со тоа и одредено решение, се користат различни дополнителни услови на равенката (1.1). На пример, таканаречените почетни услови може да се наведат на (1.2)

На десната страна на почетните услови (1.2) се наведени нумеричките вредности на функцијата и изводите, а вкупниот број на почетни услови е еднаков на бројот на дефинирани произволни константи.

Проблемот за наоѓање одредено решение за равенката (1.1) врз основа на почетните услови се нарекува проблем на Коши.

§ 2. Обични диференцијални равенки од 1 ред - основни поими.

Обична диференцијална равенка од прв ред ( n=1) има форма:
или, ако може да се реши во однос на изводот:
. Заедничка одлука y= y(x, СО)или општ интеграл
Равенките од прв ред содржат една произволна константа. Единствениот почетен услов за равенка од 1-ви ред
ви овозможува да ја одредите вредноста на константата од општо решение или од општ интеграл. Така, ќе се најде одредено решение или, што е исто, ќе се реши проблемот со Коши. Прашањето за постоењето и единственоста на решението на проблемот на Коши е едно од централните во општата теорија на обичните диференцијални равенки. За равенка од прв ред, особено, валидна е теоремата, која овде е прифатена без доказ.

Теорема 2.1.Ако во равенката функцијата
и неговиот парцијален дериват
континуирано во некој регион Драмнина XOY, и во оваа област е наведена точка
, тогаш постои единствено решение кое ги задоволува и равенката и почетната состојба
.

Геометриски, општото решение на равенката од 1-ви ред е фамилија на криви на рамнината XOY, кои немаат заеднички точки и се разликуваат едни од други во еден параметар - вредноста на константата В. Овие криви се нарекуваат интегрални криви за дадена равенка. Кривите со интегрални равенки имаат очигледно геометриско својство: во секоја точка, тангентата на тангентата на кривата е еднаква на вредноста на десната страна на равенката во оваа точка:
. Со други зборови, равенката е дадена во рамнината XOYполе на насоки на тангенти на интегрални криви. Коментар:Треба да се забележи дека на равенката.
равенката и таканаречената равенка се дадени во симетрична форма
.

§ 3. Диференцијални равенки од 1-ви ред со раздвојливи променливи.

Дефиниција.Диференцијална равенка со раздвојливи променливи е равенка на формата
(3.1)

или равенка од формата (3.2)

За да се издвојат променливите во равенката (3.1), т.е. намалете ја оваа равенка на таканаречената равенка на разделена променлива, направете го следново:

;

Сега треба да ја решиме равенката е(y)= 0 . Ако има вистинско решение y= а, Тоа y= аќе биде и решение за равенката (3.1).

Равенката (3.2) се сведува на раздвоена променлива равенка со делење со производот
:

, што ни овозможува да го добиеме општиот интеграл на равенката (3.2):
. (3.3)

Интегралните криви (3.3) ќе бидат дополнети со решенија
, доколку постојат такви решенија.

Решете ја равенката: .

Ги издвојуваме променливите:


.

Интегрирајќи, добиваме

Понатаму од равенките
И
ние најдовме x=1, y=-1. Овие решенија се приватни решенија.

§ 4. Хомогени диференцијални равенки од 1-ви ред.

Дефиниција 1.Равенката од прв ред се нарекува хомогена ако за нејзината десна страна за која било
соодносот е валиден
, наречен услов за хомогеност на функција од две променливи со нулта димензија.

Пример 1.Покажете ја таа функција
- хомогена нулта димензија.

Решение.

,

Q.E.D.

Теорема.Секоја функција
- хомогена и, обратно, секоја хомогена функција
нултата димензија се сведува на формата
.

Доказ.

Првата изјава на теоремата е очигледна, бидејќи
. Ајде да ја докажеме втората изјава. Да ставиме
, потоа за хомогена функција
, што требаше да се докаже.

Дефиниција 2.Равенка (4.1)

во која МИ Н– хомогени функции од ист степен, т.е. имаат имот за сите , се нарекува хомогена.

Очигледно, оваа равенка секогаш може да се сведе на формата
(4.2), иако за да го решите не мора да го правите ова.

Хомогена равенка се сведува на равенка со раздвојливи променливи со замена на саканата функција yспоред формулата y= zx, Каде z(x) – нова потребна функција. Откако ја извршивме оваа замена во равенката (4.2), добиваме:
или
или
.

Интегрирајќи го добиваме општиот интеграл на равенката во однос на функцијата z(x)
, кој по повеќекратна замена
го дава општиот интеграл на првобитната равенка. Покрај тоа, ако - корени на равенката
, потоа функциите
- решавање на хомогена дадена равенка. Ако
, тогаш равенката (4.2) добива форма

и станува равенка со раздвојливи променливи. Нејзините решенија се полудиректни:
.

Коментар.Понекогаш е препорачливо да се користи замена наместо горната замена x= zy.

§ 5. Диференцијални равенки сведени на хомогени.

Размислете за равенка на формата
. (5.1)

Ако
, тогаш ова е равенката со помош на замена, каде И - нови променливи, и - некои константни бројки утврдени од системот

Сведено на хомогена равенка

Ако
, тогаш равенката (5.1) добива форма

.

Верувајќи z= секира+ од страна на, доаѓаме до равенка која не содржи независна променлива.

Ајде да погледнеме примери.

Пример 1.

Интегрирајте ја равенката

и означи ја интегралната крива што минува низ точките: а) (2;2); б) (1;-1).

Решение.

Да ставиме y= zx. Потоа ди= xdz+ zdxИ

Ајде да го скратиме и собирајте членови на dxИ џ:

Ајде да ги одделиме променливите:

.

Интегрирајќи, добиваме ;

или
,
.

Се заменува овде zна , го добиваме општиот интеграл на дадената равенка во форма (5.2)
или

.

Ова е семејство на кругови
, чии центри лежат на права линија y = xа кои на почеток се тангентни на правата y + x = 0. Оваа линијаy = - x за возврат, одредено решение на равенката.

Сега режимот на проблемот на Коши:

А) ставање во општиот интеграл x=2, y=2, ние најдовме C=2,затоа бараното решение ќе биде
.

Б) ниту една од круговите (5.2) не поминува низ точката (1;-1). Но, тоа е полу-право y = - x,
поминува низ точката и го дава потребното решение.

Пример 2.Решете ја равенката: .

Решение.

Равенката е посебен случај на равенката (5.1).

Детерминанта
во овој пример
, па затоа треба да го решиме следниов систем

Решавајќи, го добиваме тоа
. Со извршување на замена во дадена равенка
, добиваме хомогена равенка. Интегрирање со помош на замена
, ние најдовме
.

Враќање на старите променливи xИ yспоред формули
, ние имаме .

§ 6. Генерализирана хомогена равенка.

Равенката М(x, y) dx+ Н(x, y) ди=0 се нарекува генерализирана хомогена ако е можно да се избере таков број к, дека левата страна на оваа равенка станува хомогена функција од одреден степен мрелативно x, y, dxИ дипод услов да xсе смета за вредноста на првата димензија, y – кти мерења , dxИ ди – соодветно нула и (к-1) ти мерења. На пример, ова би била равенката
. (6.1)

Важи според претпоставките направени во врска со мерењата

x, y, dxИ дичленови на левата страна
И диќе има димензии -2, 2 соодветно кИ к-1. Изедначувајќи ги, добиваме услов што бараниот број мора да го задоволи к: -2 = 2к=к-1. Овој услов е задоволен кога к= -1 (со ова ксите членови од левата страна на равенката што се разгледува ќе имаат димензија -2). Следствено, равенката (6.1) е генерализирана хомогена.

Генерализирана хомогена равенка се сведува на равенка со раздвојливи променливи со помош на замена
, Каде z– нова непозната функција. Дозволете ни да ја интегрираме равенката (6.1) користејќи го наведениот метод. Бидејќи к= -1, тогаш
, по што ја добиваме равенката .

Интегрирајќи го, наоѓаме
, каде
. Ова е општо решение на равенката (6.1).

§ 7. Линеарни диференцијални равенки од 1 ред.

Линеарна равенка од 1-ви ред е равенка која е линеарна во однос на саканата функција и нејзиниот извод. Изгледа како:

, (7.1)

Каде П(x) И П(x) – дадени континуирани функции на x. Доколку функцијата
, тогаш равенката (7.1) има форма:
(7.2)

и се нарекува линеарна хомогена равенка, во спротивно
се нарекува линеарна нехомогена равенка.

Линеарната хомогена диференцијална равенка (7.2) е равенка со раздвојливи променливи:

(7.3)

Изразот (7.3) е општо решение на равенката (7.2). Да се ​​најде општо решение на равенката (7.1), во кое функцијата П(x) ја означува истата функција како во равенката (7.2), применуваме техника наречена метод на варијација на произволна константа и се состои од следново: ќе се обидеме да ја избереме функцијата C=C(x) така што општото решение на линеарната хомогена равенка (7.2) би било решение на нехомогената линеарна равенка (7.1). Потоа за изводот на функцијата (7.3) добиваме:

.

Заменувајќи го пронајдениот извод со равенката (7.1), ќе имаме:

или
.

Каде
, каде што е произволна константа. Како резултат на тоа, општото решение на нехомогената линеарна равенка (7.1) ќе биде (7.4)

Првиот член во оваа формула го претставува општото решение (7.3) на линеарната хомогена диференцијална равенка (7.2), а вториот член од формулата (7.4) е одредено решение на линеарната нехомогена равенка (7.1), добиена од општата ( 7.4) со
. Овој важен заклучок го истакнуваме во форма на теорема.

Теорема.Ако е познато едно одредено решение на линеарна нехомогена диференцијална равенка
, тогаш сите други решенија ја имаат формата
, Каде
- општо решение на соодветната линеарна хомогена диференцијална равенка.

Сепак, треба да се забележи дека за решавање на линеарната нехомогена диференцијална равенка од 1-ви ред (7.1), почесто се користи друг метод, понекогаш наречен Бернули метод. Ќе бараме решение за равенката (7.1) во форма
. Потоа
. Да го замениме пронајдениот извод во првобитната равенка:
.

Да ги комбинираме, на пример, вториот и третиот член од последниот израз и да ја извлечеме функцијата u(x) зад заградата:
(7.5)

Бараме да се поништи заградата:
.

Дозволете ни да ја решиме оваа равенка со поставување на произволна константа Веднакво на нула:
. Со пронајдената функција v(x) Да се ​​вратиме на равенката (7.5):
.

Решавајќи го, добиваме:
.

Според тоа, општото решение на равенката (7.1) има форма:

§ 8. Бернулиова равенка.

Дефиниција.

Диференцијална равенка на формата
, Каде
, се нарекува Бернулиова равенка.

Под претпоставка дека
, поделете ги двете страни на Бернулиевата равенка со . Како резултат добиваме:
(8.1)

Ајде да воведеме нова функција
. Потоа
. Да ја помножиме равенката (8.1) со
и да одиме на функцијата z(x) :
, т.е. за функција z(x) доби линеарна нехомогена равенка од 1 ред. Оваа равенка се решава со помош на методите дискутирани во претходниот пасус. Наместо тоа, да го замениме со неговото општо решение z(x) изразување
, го добиваме општиот интеграл на Бернулиевата равенка, кој лесно се решава во однос на y. На
се додава раствор y(x)=0 . Равенката на Бернули, исто така, може да се реши без да се направи транзиција кон линеарна равенка со замена
и користејќи го Бернулиовиот метод, детално дискутиран во § 7. Да ја разгледаме употребата на овој метод за решавање на Бернулиовата равенка користејќи конкретен пример.

Пример.Најдете го општото решение на равенката:
(8.2)

Решение.

Според тоа, општото решение на оваа равенка има форма:
, y(x)=0.

§ 9. Диференцијални равенки во вкупни диференцијали.

Дефиниција.Ако во равенка. М(x, y) dx+ Н(x, y) ди=0 (9.1) левата страна е вкупниот диференцијал на некоја функција У(x, y) , тогаш се нарекува вкупна диференцијална равенка. Оваа равенка може да се преработи како ду(x, y)=0 , според тоа, неговиот општ интеграл е u(x, y)= в.

На пример, равенката xdy+ ydx=0 постои равенка во вкупните диференцијали, бидејќи може да се препише во форма г(xy)=0. Општиот интеграл ќе биде xy= в- произволна диференцијабилна функција. Да ја разликуваме (9.3) во однос на u
§ 10. Интегрирачки фактор.

Ако равенката М(x, y) dx + Н(x, y) ди = 0 не е тотална диференцијална равенка и има функција µ = µ(x, y) , така што откако ќе ги помножиме двете страни на равенката со неа, ја добиваме равенката

µ(Mdx + Ndy) = 0во вкупни диференцијали, т.е. µ(Mdx + Ndy)ду, потоа функцијата µ(x, y) се нарекува интегрирачки фактор на равенката. Во случај кога равенката е веќе равенка во вкупни диференцијали, претпоставуваме µ = 1.

Доколку се најде интегрирачкиот фактор µ , тогаш интеграцијата на оваа равенка се сведува на множење на двете негови страни со µ и наоѓање на општиот интеграл на добиената равенка во вкупни диференцијали.

Ако µ е континуирано диференцијабилна функција на xИ y, Тоа
.

Оттука произлегува дека интегрирачкиот фактор µ ја задоволува следната парцијална диференцијална равенка од прв ред:

(10.1).

Ако однапред се знае дека µ= µ(ω) , Каде ω – дадена функција од xИ y, тогаш равенката (10.1) се сведува на обична (и згора на тоа, линеарна) равенка со непозната функција µ на независна променлива ω :

(10.2),

Каде
, односно дропката е функција само на ω .

Решавајќи ја равенката (10.2), го наоѓаме факторот за интегрирање

, Со = 1.

Конкретно, равенката М(x, y) dx + Н(x, y) ди = 0 има интегрирачки фактор кој зависи само од x(ω = x) или само од y(ω = y), доколку соодветно се исполнети следните услови:

,

,
.

Со кликнување на копчето „Преземи архива“, ќе ја преземете датотеката што ви треба потполно бесплатно.
Пред да ја преземете оваа датотека, размислете за добрите есеи, тестови, семинарски трудови, дисертации, статии и други документи што лежат неподигнати на вашиот компјутер. Ова е ваша работа, таа треба да учествува во развојот на општеството и да им користи на луѓето. Најдете ги овие дела и поднесете ги до базата на знаење.
Ние и сите студенти, дипломирани студенти, млади научници кои ја користат базата на знаење во нивните студии и работа ќе ви бидеме многу благодарни.

За да преземете архива со документ, внесете петцифрен број во полето подолу и кликнете на копчето „Преземи архива“

Слични документи

    Коши проблеми за диференцијални равенки. График на решение на диференцијална равенка од прв ред. Равенки со раздвојливи променливи и сведување на хомогена равенка. Хомогени и нехомогени линеарни равенки од прв ред. Бернулиевата равенка.

    предавање, додадено 18.08.2012

    Основни концепти на теоријата на обични диференцијални равенки. Знак на равенка во вкупни диференцијали, конструкција на општ интеграл. Наједноставните случаи на наоѓање на интегрирачкиот фактор. Случај на множител кој зависи само од X и само од Y.

    работа на курсот, додадена 24.12.2014

    Карактеристики на диференцијалните равенки како односи меѓу функциите и нивните деривати. Доказ за теоремата за постоење и единственост на решението. Примери и алгоритам за решавање равенки во вкупни диференцијали. Интегрирачки фактор во примери.

    работа на курсот, додадена 02/11/2014

    Рикати диференцијални равенки. Општо решение на линеарна равенка. Наоѓање на сите можни решенија за Бернулиовата диференцијална равенка. Решавање равенки со раздвојливи променливи. Општи и посебни решенија на диференцијалната равенка на Клеро.

    работа на курсот, додадена 26.01.2015 година

    Равенка со раздвојливи променливи. Хомогени и линеарни диференцијални равенки. Геометриски својства на интегралните кривини. Целосен диференцијал на функција од две променливи. Определување на интегралот со Бернули методи и варијации на произволна константа.

    апстракт, додаде 24.08.2015

    Поими и решенија на наједноставните диференцијални равенки и диференцијални равенки од произволен ред, вклучувајќи ги и оние со постојани аналитички коефициенти. Системи на линеарни равенки. Асимптотичко однесување на решенија на некои линеарни системи.

    теза, додадена 06/10/2010

    Општ интеграл на равенка, примена на методот Лагранж за решавање на нехомогена линеарна равенка со непозната функција. Решавање на диференцијална равенка во параметарска форма. Ојлерова состојба, равенка од прв ред во вкупни диференцијали.

    тест, додаден на 11.02.2011 година