Хармоничните осцилации се опишани со равенката. Флуктуации. Хармонични вибрации. Равенката на хармониските осцилации. Она што се нарекува рамо на диполот

Равенка на хармоничен бран

Равенката на хармониските осцилации ја утврдува зависноста на координатата на телото од времето

Косинусниот график има максимална вредност во почетниот момент, а синусниот графикон има нулта вредност во почетниот момент. Ако почнеме да го истражуваме осцилацијата од позицијата на рамнотежа, тогаш осцилацијата ќе го повтори синусоидот. Ако почнеме да ја разгледуваме осцилацијата од позицијата на максималното отстапување, тогаш осцилацијата ќе го опише косинусот. Или таквата осцилација може да се опише со синусната формула со почетна фаза.

Промена на брзината и забрзувањето при хармониско осцилирање

Со текот на времето не се менува само координатата на телото според законот на синус или косинус. Но, таквите количини како сила, брзина и забрзување исто така се менуваат на сличен начин. Силата и забрзувањето се максимални кога осцилирачкото тело е во екстремни позиции каде поместувањето е максимално и се еднакви на нула кога телото минува низ рамнотежна положба. Брзината, напротив, во екстремните позиции е еднаква на нула, а кога телото ќе ја помине рамнотежната положба, ја достигнува својата максимална вредност.

Ако осцилацијата е опишана според законот за косинус

Ако осцилацијата е опишана според синусниот закон

Вредности за максимална брзина и забрзување

По анализата на равенките на зависност v(t) и a(t), може да се претпостави дека максималните вредности на брзината и забрзувањето се земаат кога тригонометриски факторе 1 или -1. Утврдено со формулата

§ 6. МЕХАНИЧКИ ОСЦИЛАЦИИОсновни формули

Равенката хармонични вибрации

каде X -поместување на осцилирачката точка од положбата на рамнотежа; т- време; НО,ω, φ- соодветно амплитуда, аголна фреквенција, почетна фаза на осцилации; - фаза на осцилации во моментот т.

Фреквенција на аголна осцилација

каде ν и Т се фреквенцијата и периодот на осцилациите.

Брзината на точка која прави хармонични осцилации,

Хармонично забрзување

Амплитуда НОдобиената осцилација добиена со додавање на две осцилации со исти фреквенции што се случуваат по една права линија се определува со формулата

каде а 1 И НО 2 - амплитуди на компоненти на осцилација; φ 1 и φ 2 - нивните почетни фази.

Почетната фаза φ на добиената осцилација може да се најде од формулата

Фреквенцијата на отчукувања кои произлегуваат од додавањето на две осцилации што се случуваат по истата права линија со различни, но блиски по вредност, фреквенции ν 1 и ν 2,

Равенката на траекторијата на точка која учествува во две меѓусебно нормални осцилации со амплитуди A 1 и A 2 и почетни фази φ 1 и φ 2,

Ако почетните фази φ 1 и φ 2 на компонентите на осцилацијата се исти, тогаш равенката на траекторијата ја добива формата

т.е. точката се движи во права линија.

Во случај кога фазната разлика , равенката добива форма

т.е. точката се движи по елипса.

Диференцијална равенка на хармониски вибрации на материјална точка

, или , каде што m е масата на точката; к- коефициент на квази-еластична сила ( к=Тω 2).

Вкупната енергија на материјална точка што прави хармонични осцилации,

Периодот на осцилација на тело виси на пружина (пролетно нишало),

каде м- телесна маса; к- пружина вкочанетост. Формулата важи за еластични осцилации во границите во кои е исполнет Хуковиот закон (со мала маса на пружината во споредба со масата на телото).

Периодот на осцилација на математичко нишало

каде л- должина на нишалото; е- забрзување на гравитацијата. Период на осцилација на физичко нишало

каде Ј- моментот на инерција на осцилирачкото тело околу оската

флуктуации; но- растојание на центарот на масата на нишалото од оската на осцилација;

Намалена должина на физичко нишало.

Горенаведените формули се точни за случајот на бесконечно мали амплитуди. За конечни амплитуди, овие формули даваат само приближни резултати. При амплитуди не поголеми од грешката во вредноста на периодот не надминува 1%.

Периодот на торзиони вибрации на тело виси на еластична нишка,

каде Ј- моментот на инерција на телото околу оската што се совпаѓа со еластичната нишка; к- вкочанетоста на еластичната нишка, еднаков на односотеластичниот момент што настанува кога конецот е извиткан до аголот со кој конецот е извиткан.

Диференцијална равенка на пригушени осцилации , или ,

каде р- коефициент на отпор; δ - коефициент на придушување: ;ω 0 - природна аголна фреквенција на вибрации *

Равенка на пригушена осцилација

каде A(t)- амплитуда на пригушени осцилации во моментот t;ω е нивната аголна фреквенција.

Аголна фреквенција на пригушени осцилации

О Зависност на амплитудата на пригушените осцилации од времето

Јас

каде НО 0 - амплитуда на осцилации во моментот т=0.

Логаритамско намалување на осцилацијата

каде A(t)И A(t+T)- амплитудите на две последователни осцилации разделени во времето една од друга со точка.

Диференцијална равенка на принудни вибрации

каде е надворешна периодична сила која дејствува на осцилирачка материјална точка и предизвикува принудни осцилации; Ф 0 - неговата амплитудна вредност;

Амплитуда на присилни вибрации

Резонантна фреквенција и резонантна амплитуда И

Примери за решавање проблеми

Пример 1Точката осцилира според законот x(t)=, каде А=2види Одреди почетна фаза φ ако

x(0)=cm и X , (0)<0. Построить векторную диаграмму для мо-­ мента т=0.

Решение. Ја користиме равенката на движење и го изразуваме поместувањето во моментот т=0 до почетната фаза:

Од тука ја наоѓаме почетната фаза:

* Во претходно дадените формули за хармониски осцилации, истата вредност едноставно беше означена со ω (без индекс 0).

Заменете ги дадените вредности во овој израз x(0) и НО:φ= = . Вредноста на аргументот се задоволува со две вредности на аголот:

За да одлучиме која од овие вредности на аголот φ исто така го задоволува условот, прво наоѓаме:

Заменувајќи ја вредноста во овој израз т=0 и наизменично вредностите на почетните фази и, наоѓаме

Т во ред како и секогаш А>0 и ω>0, тогаш само првата вредност од почетната фаза го задоволува условот. Така, саканата почетна фаза

Врз основа на пронајдената вредност на φ, ќе конструираме векторски дијаграм (сл. 6.1). Пример 2Материјална точка со маса Т\u003d 5 g врши хармонични осцилации со фреквенција ν =0,5 Hz. Амплитуда на осцилација А=3 cm.Одреди: 1) брзина υ поени во времето кога офсет x== 1,5 см; 2) максималната сила F max што делува на точката; 3) Сл. 6,1 вкупна енергија Еосцилирачка точка.

и ја добиваме формулата за брзина со земање на првиот временски извод на поместувањето:

За да се изрази брзината во однос на поместување, времето мора да се исклучи од формулите (1) и (2). За да го направите ова, ги квадратуваме двете равенки, ја делиме првата со НО 2 , вториот на A 2 ω 2 и додадете:

, или

Решавање на последната равенка за υ , најдете

Откако извршивме пресметки според оваа формула, добиваме

Знакот плус одговара на случајот кога насоката на брзината се совпаѓа со позитивната насока на оската X,знак минус - кога насоката на брзината се совпаѓа со негативната насока на оската X.

Поместувањето при хармониско осцилирање, покрај равенката (1), може да се определи и со равенката

Повторувајќи го истото решение со оваа равенка, го добиваме истиот одговор.

2. Силата што дејствува на точка, ја наоѓаме според вториот Њутнов закон:

каде но -забрзување на точка, кое го добиваме земајќи го временскиот извод на брзината:

Заменувајќи го изразот за забрзување во формулата (3), добиваме

Оттука и максималната вредност на силата

Заменувајќи ги во оваа равенка вредностите на π, ν, ТИ А,најдете

3. Вкупната енергија на осцилирачката точка е збир на кинетичката и потенцијалната енергија пресметана за секој момент од времето.

Најлесен начин да се пресмета вкупната енергија е во моментот кога кинетичката енергија ќе ја достигне својата максимална вредност. Во овој момент, потенцијалната енергија е нула. Значи вкупната енергија Еосцилирачката точка е еднаква на максималната кинетичка енергија

Ние ја одредуваме максималната брзина од формулата (2), поставувајќи: . Заменувајќи го изразот за брзина во формулата (4), наоѓаме

Заменувајќи ги вредностите на количините во оваа формула и правејќи пресметки, добиваме

или mcJ.

Пример 3На краевите на тенка прачка л= 1 m и тежина м 3 =400 гр мали топчиња се зајакнуваат со маси м 1=200 гр И м 2 = 300 гр. Прачката осцилира околу хоризонталната оска, нормално на

дикуларна шипка и минува низ нејзината средина (точка О на сл. 6.2). Дефинирајте период Твибрации направени од шипката.

Решение. Периодот на осцилација на физичкото нишало, кое е прачка со топчиња, се определува со односот

каде Ј- Т -неговата тежина; л ОД - растојание од центарот на масата на нишалото до оската.

Моментот на инерција на ова нишало е еднаков на збирот на моментите на инерција на топчињата Ј 1 и Ј 2 и прачка Ј 3:

Земање топки за материјални точки, ги изразуваме моментите на нивната инерција:

Бидејќи оската поминува низ средината на шипката, тогаш нејзиниот момент на инерција околу оваа оска Ј 3 = =. Замена на добиените изрази Ј 1 , Ј 2 И Ј 3 во формулата (2), го наоѓаме вкупниот момент на инерција на физичкото нишало:

Вршејќи пресметки користејќи ја оваа формула, наоѓаме

Ориз. 6.2 Масата на нишалото се состои од масите на топчињата и масата на шипката:

Растојание л ОД го наоѓаме центарот на масата на нишалото од оската на осцилација, врз основа на следните размислувања. Ако оската Xнасочете по должината на шипката и порамнете го потеклото со точката ЗА,потоа саканото растојание ле еднаква на координатата на центарот на масата на нишалото, т.е.

Замена на вредностите на количините м 1 , м 2 , м, ли вршење на пресметки, наоѓаме

Откако направивме пресметки според формулата (1), го добиваме периодот на осцилација на физичкото нишало:

Пример 4Физичкото нишало е прачка со должина л= 1 m и тежина 3 Т 1 одзакачен на еден од неговите краеви со обрач со дијаметар и маса Т 1 . Хоризонтална оска Оз

нишалото минува низ средината на шипката нормално на него (сл. 6.3). Дефинирајте период Тосцилации на такво нишало.

Решение. Периодот на осцилација на физичкото нишало се одредува со формулата

(1)

каде Ј- моментот на инерција на нишалото околу оската на осцилација; Т -неговата тежина; лВ - растојанието од центарот на масата на нишалото до оската на осцилација.

Моментот на инерција на нишалото е еднаков на збирот на моментите на инерција на шипката Ј 1 и обрач Ј 2:

(2).

Моментот на инерција на шипката во однос на оската нормална на шипката и минува низ нејзиниот центар на маса се одредува со формулата . Во овој случај t= 3Т 1 и

Го наоѓаме моментот на инерција на обрачот користејќи ја теоремата на Штајнер , каде Ј- момент на инерција за произволна оска; Ј 0 - момент на инерција за оската што минува низ центарот на масата паралелно со дадената оска; но -растојанието помеѓу наведените оски. Применувајќи ја оваа формула на обрачот, добиваме

Замена на изрази Ј 1 и Ј 2 во формулата (2), го наоѓаме моментот на инерција на нишалото околу оската на ротација:

Растојание л ОД од оската на нишалото до неговиот центар на маса е

Заменувајќи ги во формулата (1) изразите Ј, л c и масата на нишалото, го наоѓаме периодот на неговото осцилирање:

По пресметувањето со оваа формула, добиваме Т\u003d 2,17 с.

Пример 5Се додаваат две осцилации со иста насока, изразени со равенките ; X 2 = =, каде НО 1 = 1 цм, А 2 \u003d 2 cm, s, s, ω \u003d \u003d. 1. Определете ги почетните фази φ 1 и φ 2 на компонентите на осцилацијата

бани. 2. Најдете ја амплитудата НОи почетната фаза φ на добиената осцилација. Напишете ја равенката за добиената осцилација.

Решение. 1. Равенката на хармониското осцилирање има форма

Да ги трансформираме равенките дадени во условот на задачата во истата форма:

Од споредбата на изразите (2) со еднаквост (1), ги наоѓаме почетните фази на првата и втората осцилација:

Мило и мило.

2. Да се ​​одреди амплитудата НОод добиената флуктуација, погодно е да се користи векторскиот дијаграм претставен во оризот. 6.4. Според косинусовата теорема, добиваме

каде е фазната разлика на компонентите на осцилацијата.. Бидејќи , потоа, заменувајќи ги пронајдените вредности φ 2 и φ 1, добиваме рад.

Заменете ги вредностите НО 1 , НО 2 и во формулата (3) и извршете ги пресметките:

А= 2,65 см.

Тангентата на почетната фаза φ на добиената осцилација може да се одреди директно од Сл. 6.4: , од каде и почетната фаза

флуктуациинаречени движења или процеси кои се карактеризираат со одредено повторување во времето. Осцилаторните процеси се широко распространети по природа и технологија, на пример, замавнување на нишалото на часовникот, променлива електрична енергијаитн. Кога нишалото осцилира, координатата на неговиот центар на маса се менува, во случајот наизменична струјанапонот и струјата флуктуираат во колото. физичка природаосцилациите можат да бидат различни, затоа се разликуваат механички, електромагнетни и др.. Но, различните осцилаторни процеси се опишани со исти карактеристики и исти равенки. Од ова произлегува изводливоста унифициран пристапза проучување на вибрациите различна физичка природа.

Флуктуациите се нарекуваат бесплатно, ако се направени само под влијание внатрешните силидејствувајќи помеѓу елементите на системот, откако системот ќе биде изваден од рамнотежа од надворешни сили и оставен сам на себе. Секогаш бесплатни вибрации пригушени осцилации бидејќи загубите на енергија се неизбежни во реалните системи. Во идеализираниот случај на систем без загуба на енергија, слободните осцилации (кои продолжуваат произволно долго) се нарекуваат свој.

Наједноставниот тип на слободни непридушени осцилации се хармониски осцилации -флуктуации во кои флуктуирачката вредност се менува со времето според синусниот (косинус) закон. Осцилациите што се среќаваат во природата и технологијата често имаат карактер близок до хармоничен.

Хармониските вибрации се опишани со равенка наречена равенка на хармониски вибрации:

каде НО- амплитуда на флуктуации, максималната вредност на флуктуирачката вредност X; - кружна (циклична) фреквенција на природни осцилации; - почетната фаза на осцилацијата во одреден момент т= 0; - фазата на осцилацијата во моментот на времето т.Фазата на осцилацијата ја одредува вредноста на осцилирачкото количество во овој моментвреме. Бидејќи косинусот варира од +1 до -1, тогаш Xможе да земе вредности од + Апред - НО.

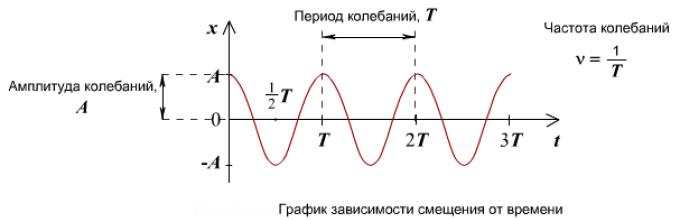
Време Т, за која системот завршува една целосна осцилација, се нарекува период на осцилација. За време на Тфазата на осцилација се зголемува за 2 π , т.е.

Каде. (14.2)

Реципроцитет на периодот на осцилација

т.е., бројот на целосни осцилации по единица време се нарекува фреквенција на осцилации. Споредувајќи ги (14.2) и (14.3) добиваме

Единицата за фреквенција е херци (Hz): 1 Hz е фреквенцијата на која се одвива една целосна осцилација за 1 s.

Системите во кои може да се појават слободни вибрации се нарекуваат осцилатори . Какви својства треба да има еден систем за да се појават слободни осцилации во него? механички системмора да има позиција на стабилна рамнотежа, при излегување кој се појавува враќање на силата кон рамнотежа. Оваа позиција одговара, како што е познато, на минимум потенцијална енергијасистеми. Да разгледаме неколку осцилаторни системи кои ги задоволуваат наведените својства.

Промените во количината се опишани со користење на законите на синус или косинус, тогаш таквите осцилации се нарекуваат хармонични. Размислете за коло направено од кондензатор (кој бил наполнет пред да се вклучи во колото) и индуктор (сл. 1).

Слика 1.

Равенката на хармониските осцилации може да се запише на следниов начин:

$q=q_0cos((\омега)_0t+(\алфа)_0)$ (1)

каде $t$-time; $q$ полнење, $q_0$-- максимално отстапување на полнењето од неговата просечна (нула) вредност за време на промените; $(\omega )_0t+(\alpha)_0$- фаза на осцилација; $(\alpha )_0$ - почетна фаза; $(\omega )_0$ - циклична фреквенција. Во текот на периодот, фазата се менува за $2\pi $.

Типска равенка:

равенката на хармониските осцилации во диференцијална форма за осцилаторно коло кое нема да содржи активен отпор.

Секаков вид на периодични осцилации може точно да се претстави како збир на хармониски осцилации, таканаречена хармонична серија.

За периодот на осцилација на коло што се состои од калем и кондензатор, ја добиваме Томсоновата формула:

Ако го разликуваме изразот (1) во однос на времето, можеме да ја добиеме формулата за функцијата $I(t)$:

Напонот преку кондензаторот може да се најде како:

Од формулите (5) и (6) следува дека јачината на струјата е понапред од напонот на кондензаторот за $\frac(\pi )(2).$

Хармоничните осцилации можат да се претстават и во форма на равенки, функции и векторски дијаграми.

Равенката (1) претставува слободни непридушени осцилации.

Равенка на пригушена осцилација

Промената на полнењето ($q$) на кондензаторските плочи во колото, земајќи го предвид отпорот (сл. 2), ќе биде опишана со диференцијална равенка од формата:

Слика 2.

Ако отпорот што е дел од колото $R \

каде $\omega =\sqrt(\frac(1)(LC)-\frac(R^2)(4L^2))$ е фреквенцијата на цикличните осцилации. $\beta =\frac(R)(2L)-$фактор на слабеење. Амплитудата на пригушените осцилации се изразува како:

Во случај кога на $t=0$ полнењето на кондензаторот е еднакво на $q=q_0$, нема струја во колото, тогаш за $A_0$ можеме да напишеме:

Фазата на осцилација во почетниот временски момент ($(\alpha )_0$) е еднаква на:

За $R >2\sqrt(\frac(L)(C))$ промената на полнењето не е осцилација, празнењето на кондензаторот се нарекува апериодично.

Пример 1

Задачата:Максималната вредност на наплатата е $q_0=10\ C$. Хармонично се менува со периодот $T= 5 c$. Определете ја максималната можна струја.

Решение:

Како основа за решавање на проблемот, користиме:

За да се најде моменталната јачина, изразот (1.1) мора да се диференцира во однос на времето:

каде што максималната (вредност на амплитудата) на тековната јачина е изразот:

Од условите на проблемот, ја знаеме амплитудната вредност на полнењето ($q_0=10\ Kl$). Треба да ја пронајдете природната фреквенција на осцилациите. Да го изразиме како:

\[(\omega)_0=\frac(2\pi)(T)\лево(1.4\десно).\]

Во овој случај, саканата вредност ќе се најде со помош на равенките (1.3) и (1.2) како:

Бидејќи сите количини во условите на проблемот се претставени во системот SI, ние ќе ги извршиме пресметките:

Одговор:$I_0=12,56\ A.$

Пример 2

Задачата:Колкав е периодот на осцилација во коло кое содржи индуктор $L=1$H и кондензатор, ако струјата во колото се менува според законот: $I\left(t\right)=-0.1sin20\pi t \ \left(A \десно)?$ Колку е капацитетот на кондензаторот?

Решение:

Од равенката на струјните осцилации, која е дадена во условите на проблемот:

гледаме дека $(\omega )_0=20\pi $, па затоа можеме да го пресметаме Периодот на осцилација користејќи ја формулата:

\ \

Според формулата на Томсон за коло што содржи индуктор и кондензатор, имаме:

Да го пресметаме капацитетот:

Одговор:$T=0,1$ c, $C=2,5\cdot (10)^(-4)F.$

Разгледавме неколку физички сосема различни системи и се уверивме дека равенките на движење се сведени на иста форма

Разликите меѓу физичките системи се манифестираат само во различни дефиниции на количината и во поинаква физичка смисла на променливата x: може да биде координата, агол, полнење, струја итн. Забележете дека во овој случај, како што произлегува од самата структура на равенката (1.18), количината секогаш има димензија на инверзно време.

Равенката (1.18) го опишува т.н хармонични вибрации.

Равенката на хармониските осцилации (1.18) е линеарна диференцијална равенкавтор ред (бидејќи го содржи вториот извод на променливата x). Линеарноста на равенката значи дека

доколку има некоја функција x(t)е решение за оваа равенка, а потоа функцијата Cx(t)ќе биде и негово решение ( Ве произволна константа);

ако функционира x 1 (t)И x 2 (t)се решенија на оваа равенка, па нивниот збир x 1 (t) + x 2 (t)исто така ќе биде решение за истата равенка.

Докажано, исто така математичка теорема, според која равенката од втор ред има две независни решенија. Сите други решенија, според својствата на линеарноста, може да се добијат како нивни линеарни комбинации. Лесно е да се провери со директна диференцијација дали независните функционираат и ја задоволуваат равенката (1.18). Значи, генералното решение на оваа равенка е:

каде C1,C2се произволни константи. Ова решение може да се претстави и во друга форма. Ја воведуваме количината

и дефинирај го аголот како:

Тогаш општото решение (1.19) се запишува како

Според формулите за тригонометрија, изразот во загради е

Конечно пристигнуваме општо решение на равенката на хармониските осцилациикако:

Негативна вредност Аповикани амплитуда на осцилација, - почетната фаза на осцилацијата. Целиот косинус аргумент - комбинацијата - се нарекува фаза на осцилација.

Изразите (1.19) и (1.23) се совршено еквивалентни, така што можеме да користиме било кој од нив од причини на едноставност. Двете решенија се периодични функциивреме. Навистина, синусот и косинусот се периодични со точка . Затоа, различни состојби на систем кој врши хармонски осцилации се повторуваат по одреден временски период т*, за која фазата на осцилација добива прираст кој е повеќекратен од :

Оттука произлегува дека

Најмалку од овие времиња

повикани период на осцилација (Сл. 1.8), а - неговиот кружни (циклични) фреквенција.

Ориз. 1.8.

Тие исто така користат фреквенција двоумење

Според тоа, кружната фреквенција е еднаква на бројот на осцилации по секунди.

Значи, ако системот на време тсе карактеризира со вредноста на променливата x (t),тогаш, истата вредност, променливата ќе ја има по одреден временски период (сл. 1.9), т.е

Истата вредност, се разбира, ќе се повтори по некое време. 2Т, ЗТитн.

Ориз. 1.9. Период на осцилации

Општото решение вклучува две произволни константи ( C1, C2или А, а), чии вредности треба да се одредат со два почетни услови. Обично (иако не мора) нивната улога ја играат почетните вредности на променливата x(0)и неговиот дериват.

Да земеме пример. Нека решението (1.19) на равенката на хармониските осцилации го опишува движењето на пружинското нишало. Вредностите на произволните константи зависат од начинот на кој го извадивме нишалото од рамнотежа. На пример, ја повлековме пружината на далечина и ја ослободи топката без почетна брзина. Во овој случај

Замена t = 0во (1.19), ја наоѓаме вредноста на константата Од 2

Така, решението изгледа вака:

Брзината на оптоварувањето се наоѓа со диференцијација во однос на времето

Замена овде т = 0, најдете ја константата Од 1:

Конечно

Споредувајќи се со (1.23), откриваме дека е амплитудата на осцилацијата, а неговата почетна фаза е еднаква на нула: .

Сега го вадиме нишалото од рамнотежа на друг начин. Ајде да го удриме товарот за да добие почетна брзина, но практично да не се движи при ударот. Потоа имаме други почетни услови:

нашето решение изгледа како

Брзината на товарот ќе се промени според законот:

Ајде да го ставиме овде: