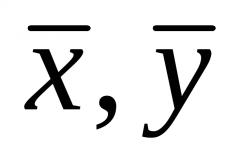Пресметка на проекцијата на вектор на оска. Проекција на сила на оската. Проекција на векторскиот збир на сили на оската. Скаларни и векторски величини

Вовед……………………………………………………………………………………… 3

1. Вредност на векторот и скаларот……………………………………….4

2. Дефиниција на проекција, оска и координата на точка…………………….5

3. Проекција на векторот на оската…………………………………………………………………………………

4. Основна формула векторска алгебра……………………………..8

5. Пресметка на модулот на векторот од неговите проекции…………………………9

Заклучок………………………………………………………………………………….11

Литература……………………………………………………………………………………………………………………………………………………….

Вовед:

Физиката е нераскинливо поврзана со математиката. Математиката и дава на физиката средства и техники за општо и прецизно изразување на односот помеѓу физичките величини, кои се откриени како резултат на експеримент или теоретско истражување На крајот на краиштата, главниот метод на истражување во физиката е експериментален. Ова значи дека научникот открива пресметки користејќи мерења. Означува врска помеѓу различни физички величини. Потоа, сè е преведено на јазикот на математиката. Формирана математички модел. Физиката е наука која ги проучува наједноставните и во исто време најопштите закони. Задачата на физиката е да создаде таква слика во нашите умови физичкиот свет, што најцелосно ги рефлектира неговите својства и обезбедува такви односи помеѓу елементите на моделот што постојат помеѓу елементите.

Значи, физиката создава модел на светот околу нас и ги проучува неговите својства. Но, секој модел е ограничен. При креирањето модели на одредена појава се земаат предвид само својствата и врските кои се суштински за даден опсег на појави. Ова е уметност на научникот - да ја избере главната работа од сета различност.

Физичките модели се математички, но математиката не е нивната основа. Квантитативните односи помеѓу физичките величини се одредуваат како резултат на мерења, набљудувања и експериментални студии и се изразуваат само на јазикот на математиката. Сепак, не постои друг јазик за конструирање физички теории.

1. Значење на вектор и скалар.

Во физиката и математиката, вектор е величина што се карактеризира со нејзината нумеричка вредност и насока. Во физиката, постојат многу важни количини кои се вектори, на пример, сила, позиција, брзина, забрзување, вртежен момент, моментум, јачина на електричното и магнетното поле. Тие можат да се споредат со други количини како што се масата, волуменот, притисокот, температурата и густината, кои можат да се опишат со обичен број и се нарекуваат " скалари".

Тие се напишани или со редовни букви или со бројки (a, b, t, G, 5, −7....). Скаларните количини може да бидат позитивни или негативни. Во исто време, некои предмети на проучување може да имаат такви својства што целосен описЗа кои познавањето само на нумеричка мерка се покажува недоволно, потребно е и да се карактеризираат овие својства по насока во просторот. Ваквите својства се карактеризираат со векторски величини (вектори). Векторите, за разлика од скаларите, се означуваат со задебелени букви: a, b, g, F, C....
Честопати, векторот се означува со буква со редовен (незадебелен) фонт, но со стрелка над него:

Покрај тоа, вектор често се означува со пар букви (обично со големи букви), при што првата буква го означува почетокот на векторот, а втората неговиот крај.

Модулот на векторот, односно должината на насочена права линија, се означува со истите букви како и самиот вектор, но со нормално (не задебелено) пишување и без стрелка над нив, или на ист начин како вектор (т.е. задебелени или правилни, но со стрелки), но тогаш ознаката на векторот е затворена во вертикални цртички.
Вектор е комплексен објект кој истовремено се карактеризира и со големина и со насока.

Исто така, нема позитивни и негативни вектори. Но, векторите можат да бидат еднакви еден на друг. Ова е кога, на пример, a и b имаат исти модули и се насочени во иста насока. Во овој случај, ознаката е вистинита а= б. Исто така, треба да се има предвид дека на векторскиот симбол може да му претходи знак минус, на пример - c, меѓутоа, овој знак симболично покажува дека векторот -c го има истиот модул како векторот c, но е насочен спротивно. насока.

Векторот -c се нарекува спротивен (или инверзен) на векторот c.
Во физиката, секој вектор е исполнет со специфична содржина, а кога се споредуваат вектори од ист тип (на пример, сили), точките на нивната примена исто така можат да бидат значајни.

2. Определување на проекцијата, оската и координатата на точката.

Оска- Ова е права линија на која и се дава некаков правец.
Оска се означува со некоја буква: X, Y, Z, s, t... Обично на оската (произволно) се избира точка, која се нарекува почеток и по правило се означува со буквата О. Од оваа точка се мерат растојанијата до други точки од интерес за нас.

Проекција на точкана оска е основата на нормалната нацртана од оваа точка на дадена оска. Односно, проекцијата на точка на оската е точка.

Точка координатана оваа оска се нарекува број, апсолутна вредностшто е еднакво на должината на сегментот на оската (на избраната скала) затворен помеѓу почетокот на оската и проекцијата на точката на оваа оска. Овој број се зема со знак плус ако проекцијата на точката се наоѓа во правец на оската од нејзиното потекло и со знак минус ако е во спротивна насока.

3. Проекција на векторот на оската.

Проекцијата на вектор на оска е вектор кој се добива со множење на скаларната проекција на вектор на оваа оска и единечниот вектор на оваа оска. На пример, ако x е скаларна проекција на векторот a на оската X, тогаш x ·i е неговата векторска проекција на оваа оска.

Да означиме векторска проекцијаисто како и самиот вектор, но со индекс на оската на која е проектиран векторот. Така, векторската проекција на векторот a на оската X ја означуваме како x (задебелена буква што го означува векторот и знакот на името на оската) или

(ниско задебелена буква што означува вектор, но со стрелка на врвот (!) и знак за името на оската).

Скаларна проекцијавектор по оска се нарекува број, чија апсолутна вредност е еднаква на должината на сегментот на оската (на избраната скала) затворен помеѓу проекциите на почетната точка и крајната точка на векторот. Обично наместо изразот скаларна проекцијатие едноставно велат - проекција. Проекцијата се означува со истата буква како и проектираниот вектор (во нормално, незадебелено пишување), со помал индекс (по правило) на името на оската на која се проектира овој вектор. На пример, ако вектор е проектиран на оската X А,тогаш неговата проекција се означува со x. При проектирање на истиот вектор на друга оска, ако оската е Y, нејзината проекција ќе биде означена со y.

Да се пресмета проекцијата векторна оската (на пример, оската X), потребно е да се одземе координатата на почетната точка од координатата на нејзината крајна точка, т.е.

a x = x k − x n.

Проекцијата на вектор на оска е бројка.Покрај тоа, проекцијата може да биде позитивна ако вредноста x k е поголема од вредноста x n,

негативен ако вредноста x k помала од вредноста x n

и еднакво на нула ако x k е еднакво на x n.

Проекцијата на векторот на оската може да се најде и со познавање на модулот на векторот и аголот што го прави со оваа оска.

Од сликата е јасно дека a x = a Cos α

Односно, проекцијата на векторот на оската е еднаква на производот од модулот на векторот и косинусот на аголот помеѓу насоката на оската и векторска насока. Ако аголот е акутен, тогаш
Cos α > 0 и a x > 0, и ако е тап, тогаш косинусот на тапиот агол е негативен, а проекцијата на векторот на оската исто така ќе биде негативна.

Аглите измерени од оската спротивно од стрелките на часовникот се сметаат за позитивни, а аглите измерени долж оската се негативни. Меѓутоа, бидејќи косинус е парна функција, односно Cos α = Cos (− α), кога се пресметуваат проекциите, аглите може да се бројат и во насока на стрелките на часовникот и спротивно од стрелките на часовникот.

За да се најде проекцијата на векторот на оската, модулот на овој вектор мора да се помножи со косинус на аголот помеѓу насоката на оската и насоката на векторот.

4. Основна формула на векторска алгебра.

Да го проектираме векторот a на оските X и Y на правоаголниот координатен систем. Ајде да ги најдеме векторските проекции на векторот a на овие оски:

a x = a x ·i, и y = a y ·j.

Но во согласност со правилото за векторско собирање

a = a x + a y.

a = a x i + a y j.

Така, ние изразивме вектор во однос на неговите проекции и вектори на правоаголниот координатен систем (или во однос на неговите векторски проекции).

Векторските проекции a x и a y се нарекуваат компоненти или компоненти на векторот a. Операцијата што ја извршивме се нарекува разложување на вектор по оските на правоаголен координатен систем.

Ако векторот е даден во просторот, тогаш

a = a x i + a y j + a z k.

Оваа формула се нарекува основна формула на векторска алгебра. Се разбира, може да се напише вака.

Во оваа статија ќе ја разбереме проекцијата на векторот на оската и ќе научиме како да ја пронајдеме нумеричката проекција на векторот. Прво, ќе дадеме дефиниција за проекцијата на вектор на оска, ќе воведеме нотација, а исто така ќе обезбедиме и графичка илустрација. После ова, ќе ја искажеме дефиницијата за нумеричка проекција на вектор на оска, ќе разгледаме методи за нејзино наоѓање и ќе покажеме решенија за неколку примери во кои е неопходно да се најде нумеричка проекција на вектор на оска.

Навигација на страницата.

Проекција на вектор на оска – дефиниција, ознака, илустрации, пример.

Да почнеме со некои општи информации.

Оската е права линија за која е означена насока. Така, проекцијата на вектор на оска и проекцијата на вектор на насочена линија се едно исто.

Проекцијата на вектор на оска може да се смета во две значења: геометриска и алгебарска. ВО геометриска смислапроекцијата на вектор на оска е вектор, а во алгебарскиот е број. Често оваа дистинкција не е експлицитно наведена, туку се разбира од контекстот. Ние нема да ја игнорираме оваа разлика: ќе го користиме терминот „“ кога зборуваме за проекција на вектор во геометриска смисла, и терминот „“ кога зборуваме за проекција на вектор во алгебарска смисла (на следниот став од овој член е посветен на нумеричката проекција на вектор на оска).

Сега преминуваме кон одредување на проекцијата на векторот на оската. За да го направите ова, нема да боли да се повтори.

Дозволете ни да ни биде дадена L оска и ненулти вектор на рамнина или во тродимензионален простор. Да ги означиме проекциите на точките A и B на правата L, соодветно, како A 1 и B 1 и да конструираме вектор. Гледајќи напред, да речеме дека векторот е проекција на вектор на оската L.

Дефиниција.

Проекција на вектор на оскае вектор чиј почеток и крај се, соодветно, проекциите на почетокот и крајот на даден вектор.

Проекцијата на векторот на оската L се означува како .

За да конструирате проекција на вектор на оската L, треба да ги спуштите перпендикулите од точките А и Б на насочената права линија L - основите на овие перпендикулари ќе го дадат почетокот и крајот на саканата проекција.

Да дадеме пример за векторска проекција на оска.

Нека се воведе правоаголен координатен систем Oxy на рамнината и нека биде одредена точка. Да го прикажеме векторот на радиусот на точката M 1 и да ги конструираме неговите проекции на координатните оски Ox и Oy. Очигледно, тие се вектори со координати и, соодветно.

Често може да слушнете за проекцијата на еден вектор на друг вектор не-нулта, или за проекцијата на вектор на насоката на векторот. Во овој случај, мислиме на проекција на векторот на одредена оска, чија насока се совпаѓа со насоката на векторот (општо, има бескрајно многу оски чии насоки се совпаѓаат со насоката на векторот). Проекцијата на векторот на права линија, чија насока се одредува со векторот, се означува како .

Забележете дека ако аголот помеѓу векторите и е остар, тогаш векторите и се конасочни. Ако аголот помеѓу векторите и е тап, тогаш векторите и се спротивно насочени. Ако векторот е нула или нормално на векторот, тогаш проекцијата на векторот на права линија, чија насока е одредена од векторот, е нулта вектор.

Нумеричка проекција на вектор на оска - дефиниција, ознака, примери за локација.

Нумеричката карактеристика на проекцијата на вектор на оска е нумеричката проекција на овој вектор на дадена оска.

Дефиниција.

Нумеричка проекција на вектор на оскае број кој е еднаков на производот од должината на даден вектор и косинус на аголот помеѓу овој вектор и векторот што ја одредува насоката на оската.

Нумеричката проекција на векторот на оската L се означува како (без стрелката горе), а нумеричката проекција на векторот на оската дефинирана со векторот е означена како .

Во оваа нотација, дефиницијата на нумеричката проекција на вектор на линија насочена како вектор ќе има форма , каде е должината на векторот, е аголот помеѓу векторите и .

Значи го имаме првиот формула за пресметување на нумеричка проекција на вектор: . Оваа формула се применува кога се познати должината на векторот и аголот помеѓу векторите. Несомнено, оваа формула може да се примени кога се познати координатите на векторите и во однос на даден правоаголен координатен систем, но во овој случај попогодно е да се користи друга формула, која ќе ја добиеме подолу.

Пример.

Пресметај ја нумеричката проекција на векторот на права насочена како вектор ако должината на векторот е 8, а аголот помеѓу векторите и е еднаков на .

Решение.

Од проблематичните услови што ги имаме . Останува само да се примени формулата за да се одреди потребната нумеричка проекција на векторот:

Одговор:

Ние го знаеме тоа , каде е скаларниот производ на вектори и . Потоа формулата , кој ни овозможува да ја најдеме нумеричката проекција на векторот на линија насочена како вектор, ќе има форма . Односно, можеме да формулираме друга дефиниција за нумеричката проекција на вектор на оска, што е еквивалентно на дефиницијата дадена на почетокот на овој став.

Дефиниција.

Нумеричка проекција на вектор на оска, чија насока се совпаѓа со насоката на векторот, е односот на скаларниот производ на векторите и должината на векторот.

Удобно е да се користи добиената формула на формата за да се најде нумеричката проекција на векторот на права линија, чија насока се совпаѓа со насоката на векторот, кога се познати координатите на векторите. Ова ќе го покажеме при решавање на примери.

Пример.

Познато е дека векторот ја одредува насоката на оската L. Најдете ја нумеричката проекција на векторот на оската L.

Решение.

Формулата во координатна форма е , каде и . Го користиме за да ја најдеме потребната нумеричка проекција на векторот на оската L:

Одговор:

Пример.

Во однос на правоаголниот координатен систем Oxyz, два вектори се дадени во тродимензионален простор И . Најдете ја нумеричката проекција на векторот на оската L, чија насока се совпаѓа со насоката на векторот.

Решение.

По векторски координати И можеме да го пресметаме скаларниот производ на овие вектори: . Должината на векторот од неговите координати се пресметува со следнава формула . Тогаш формулата за определување на нумеричката проекција на векторот на оската L во координати има форма .

Ајде да го примениме:

Одговор:

Сега да ја добиеме врската помеѓу нумеричката проекција на векторот на оската L, чија насока е одредена од векторот, и должината на проекцијата на векторот на оската L. За да го направите ова, ја прикажуваме оската L, ги исцртуваме векторите и од точка што лежи на L, спуштаме нормална од крајот на векторот до правата линија L и конструираме проекција на векторот на оската L. Во зависност од мерката на аголот помеѓу векторите и следните пет опции се можни:

Во првиот случај очигледно е дека, значи, тогаш .

Во вториот случај, во означениот правоаголен триаголникод дефиницијата за косинус на агол имаме , оттука, .

Во третиот случај, очигледно е дека, и , затоа, и .

Во четвртиот случај, од дефиницијата на косинус на агол произлегува дека , каде .

Во вториот случај, значи, тогаш
.

Следната дефиниција за нумеричка проекција на вектор на оска ги комбинира добиените резултати.

Дефиниција.

Нумеричка проекција на векторот на оската L, насочен како вектор, ова е

Пример.

Должината на проекцијата на векторот на оската L, чија насока е одредена од векторот, е еднаква на . Која е нумеричката проекција на векторот на оската L ако аголот помеѓу векторите и е еднаков на радијани.

А. Проекцијата на точката А на оската PQ (сл. 4) е основата a на нормалната отфрлена од дадена точка на дадена оска. Оската на која проектираме се нарекува оска на проекција.

б. Нека се дадени две оски и вектор A B, прикажани на сл. 5.

Вектор чиј почеток е проекција на почетокот и чиј крај е проекција на крајот на овој вектор се нарекува проекција на векторот A B на оската PQ.

Понекогаш индикаторот PQ не е напишан на дното, тоа се прави во случаи кога, освен PQ, нема друг оперативен систем на кој би можел да биде дизајниран.

Со. Теорема I. Големините на векторите што лежат на една оска се поврзани како големини на нивните проекции на која било оска.

Нека се дадени оските и векторите наведени на сл.6 Од сличноста на триаголниците јасно се гледа дека должините на векторите се поврзани како должини на нивните проекции, т.е.

Бидејќи векторите на цртежот се насочени во различни страни, тогаш нивните вредности имаат различни знаци, затоа,

Очигледно, големините на проекциите исто така имаат различни знаци:

заменувајќи го (2) во (3) во (1), добиваме

Свртувајќи ги знаците, добиваме

Ако векторите се подеднакво насочени, тогаш нивните проекции исто така ќе бидат во иста насока; нема да има знаци за минус во формулите (2) и (3). Заменувајќи ги (2) и (3) со еднаквост (1), веднаш добиваме еднаквост (4). Значи, теоремата е докажана за сите случаи.

г. Теорема II. Големината на проекцијата на векторот на која било оска е еднаква на големината на векторот помножена со косинус на аголот помеѓу оската на проекциите и оската на векторот . 7. Да конструираме вектор со иста насока како и неговата оска и да го нацртаме, на пример, од точката на пресек на оските. Нека нејзината должина е еднаква на една. Потоа нејзината големина

Проекцијавектор на оска е вектор кој се добива со множење на скаларната проекција на векторот на оваа оска и единечниот вектор на оваа оска. На пример, ако x - скаларна проекцијавектор Адо оската X, потоа x јас- неговата векторска проекција на оваа оска.

Да означиме векторска проекцијаисто како и самиот вектор, но со индекс на оската на која е проектиран векторот. Значи, векторската проекција на векторот Ана X оската што ја означуваме А x( мастибуква што означува вектор и знак на името на оската) или (ниско задебелена буква што означува вектор, но со стрелка на врвот (!) и знак на името на оската).

Да се пресмета проекцијата векторна оската (на пример, оската X), потребно е да се одземе координатата на почетната точка од координатата на нејзината крајна точка, т.е.
a x = x k − x n.
Проекцијата на вектор на оска е бројка.Покрај тоа, проекцијата може да биде позитивна ако вредноста x k е поголема од вредноста x n,

негативен ако вредноста x k е помала од вредноста x n

и еднакво на нула ако x k е еднакво на x n.

Проекцијата на векторот на оската може да се најде и со познавање на модулот на векторот и аголот што го прави со оваа оска.

Од сликата е јасно дека a x = a Cos α

односно, проекцијата на векторот на оската е еднаква на производот од модулот на векторот и косинусот на аголот помеѓу насоката на оската и векторска насока. Ако аголот е акутен, тогаш
Cos α > 0 и a x > 0, и ако е тап, тогаш косинусот на тапиот агол е негативен, а проекцијата на векторот на оската исто така ќе биде негативна.

Векторски координатисе коефициентите на единствената можна линеарна комбинација на базни вектори во избраниот координатен систем, еднакви на овој вектор.

каде се координатите на векторот.

Производ со точкивектори

Скаларен производ на вектори[- во конечни-димензионални векторски простор се дефинира како збир од производите на идентични компоненти што се множат вектори.

На пример, S.p.v. а = (а 1 , ..., a n) И б = (б 1 , ..., b n):

(а , б ) = а 1 б 1 + а 2 б 2 + ... + a n b n

Решавањето на проблемите за рамнотежата на силите што се конвергираат со конструирање полигони со затворена сила вклучува гломазни конструкции. Универзален метод за решавање на вакви проблеми е да се премине кон одредување на проекциите на дадените сили на координатните оски и работење со овие проекции. Оската е права линија на која и е доделена одредена насока.

Проекцијата на векторот на оската е скаларна величина, која се определува со сегментот на оската отсечен од нормалните спуштени на неа од почетокот и крајот на векторот.

Векторската проекција се смета за позитивна ако насоката од почетокот на проекцијата до нејзиниот крај се совпаѓа со позитивната насока на оската. Векторската проекција се смета за негативна ако насоката од почетокот на проекцијата до нејзиниот крај е спротивна на позитивната насока на оската.

Така, проекцијата на силата на координатната оска е еднаква на производот на модулот на сила и косинус на аголот помеѓу векторот на сила и позитивната насока на оската.

Да разгледаме голем број случаи на проектирање сили на оска:

Вектор на сила Ф(сл. 15) е со позитивна насока на оската x акутен агол.

За да ја пронајдеме проекцијата, од почетокот и крајот на векторот на сила ги спуштаме нормалните на оската ох; добиваме

1. Fx = Ф cos α

Проекцијата на векторот во овој случај е позитивна

Сила Ф(сл. 16) е со позитивна насока на оската Xтап агол α.

Потоа Ф x = Ф cos α, но бидејќи α = 180 0 - φ,

Ф x = Ф cos α = Ф cos180 0 - φ =- Ф cos φ.

Проекција на сила Фпо оска охво овој случај тоа е негативно.

Сила Ф(сл. 17) нормално на оската ох.

Проекција на силата F на оската Xеднаква на нула

Ф x = Ф cos 90° = 0.

Сила лоцирана во авионот како(сл. 18), може да се проектира на две координатни оски ОИ ох.

Сила Фможе да се подели на компоненти: Ф x и Ф y. Векторски модул Ф x е еднаква на проекцијата на векторот Фпо оска вол, и векторскиот модул Ф y е еднаква на проекцијата на векторот Фпо оска ох.

Од Δ OAV: Ф x = Ф cos α, Ф x = Фгрев α.

Од Δ OAS: Ф x = Ф cos φ, Ф x = Фгрев φ.

Големината на силата може да се најде со помош на Питагоровата теорема:

Проекцијата на векторска сума или резултант на која било оска е еднаква на алгебарскиот збир на проекциите на збировите на векторите на истата оска.

Размислете за силите што се спојуваат Ф 1 , Ф 2 , Ф 3, и Ф 4, (сл. 19, а). Геометрискиот збир или резултатот на овие сили Фопределена со страната на затворање на силниот многуаголник

Да паднеме од темињата на многуаголникот на силата до оската xперпендикулари.

Со оглед на добиените проекции на сили директно од завршената конструкција имаме

Ф= Ф 1x+ Ф 2x+ Ф 3x+ Ф 4x

каде n е бројот на векторски членови. Нивните проекции влегуваат во горната равенка со соодветниот знак.

Во рамнина, геометрискиот збир на сили може да се проектира на две координатни оски, а во просторот, соодветно, на три.