По дефиниција, диференцијалот (првиот диференцијал) на функцијата се пресметува со формулата  Ако
Ако  – независна променлива.
– независна променлива.
ПРИМЕР.
Да покажеме дека формата на првиот диференцијал останува непроменета (е непроменета) дури и во случај кога аргументот на функцијата  самата по себе е функција, односно за комплексна функција
самата по себе е функција, односно за комплексна функција .
.
Нека  се разликуваат, тогаш по дефиниција
се разликуваат, тогаш по дефиниција
Згора на тоа, тоа требаше да се докаже.
ПРИМЕРИ.

Докажаната непроменливост на формата на првиот диференцијал ни овозможува да го претпоставиме тоа  односно изводот е еднаков на односот на диференцијалот на функцијата спрема диференцијалот на нејзиниот аргумент, без разлика дали аргументот е независна променлива или функција.
односно изводот е еднаков на односот на диференцијалот на функцијата спрема диференцијалот на нејзиниот аргумент, без разлика дали аргументот е независна променлива или функција.
Диференцијација на параметарски одредена функција
Нека функционира If  има на снимање
има на снимање  спротивното, тогаш
спротивното, тогаш  Потоа еднаквостите
Потоа еднаквостите  дефинирани на сетот
дефинирани на сетот  функцијата одредена параметарски,
функцијата одредена параметарски,  –
параметар (средна променлива).
–
параметар (средна променлива).
ПРИМЕР.  .
.

|
y |
x Конструираната крива се нарекувациклоид (Сл. 25)
и е траекторија на точка на круг со радиус 1, која се тркала без да се лизга по оската OX.КОМЕНТАР
ПРИМЕРИ.
 – . Понекогаш, но не секогаш, параметар може да се елиминира од равенките на параметарската крива.параметарски равенки
– . Понекогаш, но не секогаш, параметар може да се елиминира од равенките на параметарската крива.параметарски равенки 
 кругови, бидејќи очигледно
кругови, бидејќи очигледно 
 –параметриски равенки на елипсата, бидејќи
–параметриски равенки на елипсата, бидејќи 
–параметриски равенки на парабола

Ајде да го најдеме изводот на функцијата дефинирана параметарски:  .
.
Изводот на функција назначена параметарски е исто така функција одредена параметарски:ДЕФИНИЦИЈА
. Вториот извод на функцијата е изводот на нејзиниот прв извод.  Дериват
Дериват  .
.
тиот ред е изводот на неговиот дериват на ред  Означи деривати на вториот и
Означи деривати на вториот и
- вака по ред:  Од дефиницијата на вториот извод и правилото за диференцијација на параметарски дефинирана функција произлегува дека
Од дефиницијата на вториот извод и правилото за диференцијација на параметарски дефинирана функција произлегува дека  За да го пресметате третиот извод, треба да го претставите вториот извод во форма
За да го пресметате третиот извод, треба да го претставите вториот извод во форма
ПРИМЕРи повторно употребете го добиеното правило. Слично се пресметуваат деривати од повисок ред.
 .
.
. Најдете ги изводите од прв и втор ред на функцијата
Основни теореми на диференцијално сметањеТЕОРЕМА  (Фарма). Нека функцијата
(Фарма). Нека функцијата  има во точка
има во точка  екстремни. Доколку постои
екстремни. Доколку постои 
, ТоаДОКАЗ  . Нека
. Нека  , во чии рамки
, во чии рамки  т.е
т.е  – прираст
– прираст  во точката
во точката  . По дефиниција
. По дефиниција  Ајде да пресметаме еднострани деривати во точката
Ајде да пресметаме еднострани деривати во точката  :
:
 со теоремата за премин до границата во нееднаквост,
со теоремата за премин до границата во нееднаквост,
бидејќи 
 , бидејќи
, бидејќи  Но според условот
Но според условот  постои, затоа левиот извод е еднаков на десниот, а тоа е можно само ако
постои, затоа левиот извод е еднаков на десниот, а тоа е можно само ако
Претпоставката дека  – максималната поен води кон истото.
– максималната поен води кон истото.
Геометриско значење на теоремата:
Основни теореми на диференцијално сметање(Рола). Нека функцијата  континуирано
континуирано  , диференцијабилна
, диференцијабилна  И
И  тогаш има
тогаш има  такви што
такви што 
, Тоа. Бидејќи  континуирано
континуирано  , потоа со втората теорема на Вајерштрас достигнува во
, потоа со втората теорема на Вајерштрас достигнува во  нивните најголеми
нивните најголеми  а најмалку
а најмалку  вредности или на крајните точки или на краевите на сегментот.
вредности или на крајните точки или на краевите на сегментот.
1. Нека  , Потоа
, Потоа
2. Нека  Бидејќи
Бидејќи  или
или  , или
, или  се достигнува во екстремната точка
се достигнува во екстремната точка  , но според теоремата на Ферма
, но според теоремата на Ферма  Q.E.D.
Q.E.D.
Основни теореми на диференцијално сметање(Лагранж). Нека функцијата  континуирано
континуирано  и диференцијабилни
и диференцијабилни  , тогаш има
, тогаш има  такви што
такви што  .
.
Геометриско значење на теоремата:
Бидејќи  , тогаш секантата е паралелна со тангентата. Така, теоремата вели дека постои тангента паралелна на секантата што минува низ точките А и Б.
, тогаш секантата е паралелна со тангентата. Така, теоремата вели дека постои тангента паралелна на секантата што минува низ точките А и Б.
, Тоа. Преку точките А  и Б
и Б  Ајде да нацртаме секанта AB. Нејзината равенка
Ајде да нацртаме секанта AB. Нејзината равенка  Размислете за функцијата
Размислете за функцијата
 – растојанието помеѓу соодветните точки на графикот и на секантата AB.
– растојанието помеѓу соодветните точки на графикот и на секантата AB.
1.
 континуирано
континуирано  како разлика на континуираните функции.
како разлика на континуираните функции.
2.
 диференцијабилна
диференцијабилна  како разлика на диференцијабилните функции.
како разлика на диференцијабилните функции.
3.

Средства,  ги задоволува условите од теоремата на Рол, па затоа постои
ги задоволува условите од теоремата на Рол, па затоа постои  такви што
такви што
Теоремата е докажана.
КОМЕНТАР.Формулата се нарекува Формулата на Лагранж.
Основни теореми на диференцијално сметање(Коши). Оставете ги функциите  континуирано
континуирано  , диференцијабилна
, диференцијабилна  И
И  , тогаш има поента
, тогаш има поента  такви што
такви што  .
.
, Тоа. Да го покажеме тоа  . Ако
. Ако  , потоа функцијата
, потоа функцијата  би ги задоволил условите од теоремата на Роле, па би имало точка
би ги задоволил условите од теоремата на Роле, па би имало точка  такви што
такви што  – контрадикторност на состојбата. Средства,
– контрадикторност на состојбата. Средства,  , и двете страни на формулата се дефинирани. Ајде да погледнеме помошна функција.
, и двете страни на формулата се дефинирани. Ајде да погледнеме помошна функција.
 континуирано
континуирано  , диференцијабилна
, диференцијабилна  И
И  т.е
т.е  ги задоволува условите од теоремата на Рол. Потоа, постои точка
ги задоволува условите од теоремата на Рол. Потоа, постои точка  , во која
, во која  , Но
, Но
Q.E.D.
Докажаната формула се нарекува Коши формула.
Правилото на L'Hopital(Л'Хопитал-Бернули теорема). Оставете ги функциите  континуирано
континуирано  , диференцијабилна
, диференцијабилна  ,
, И
И  . Покрај тоа, постои конечна или бесконечна
. Покрај тоа, постои конечна или бесконечна  .
.
Потоа постои 
, Тоа. Бидејќи по услов  , потоа дефинираме
, потоа дефинираме  во точката
во точката  , под претпоставка
, под претпоставка  Потоа
Потоа  ќе стане континуирано
ќе стане континуирано  . Да го покажеме тоа
. Да го покажеме тоа 
 Да претпоставиме дека
Да претпоставиме дека  тогаш има
тогаш има  такви што
такви што  , бидејќи функцијата
, бидејќи функцијата  на
на  ги задоволува условите од теоремата на Рол. Но според условот
ги задоволува условите од теоремата на Рол. Но според условот  – контрадикторност. Затоа
– контрадикторност. Затоа 
 . Функции
. Функции  ги задоволува условите од теоремата на Коши на кој било интервал
ги задоволува условите од теоремата на Коши на кој било интервал  , кој е содржан во
, кој е содржан во  . Ајде да ја напишеме формулата на Коши:
. Ајде да ја напишеме формулата на Коши:
 ,
,
 .
.
Од тука имаме:  , бидејќи ако
, бидејќи ако  екстремни. Доколку постои
екстремни. Доколку постои  .
.
Редизајнирајќи ја променливата во последната граница, го добиваме потребното:

ЗАБЕЛЕШКА 1. Правилото на L'Hopital останува валидно дури и кога  И
И  .
.  Тоа ни овозможува да ја откриеме не само неизвесноста на типот
Тоа ни овозможува да ја откриеме не само неизвесноста на типот  :
:
 .
.
, но и типот. Доколку по примената на правилото на L'Hopital не се открие неизвесноста, тогаш треба да се примени повторно.
ПРИМЕР.
и е траекторија на точка на круг со радиус 1, која се тркала без да се лизга по оската OX. 3 . Правилото на L'Hopital е универзален начин за откривање на несигурностите, но постојат граници што може да се откријат со користење само на една од претходно проучуваните конкретни техники.
Но, очигледно  , бидејќи степенот на броителот е еднаков на степенот на именителот, и границата еднаков на односоткоефициенти на повисоки сили
, бидејќи степенот на броителот е еднаков на степенот на именителот, и границата еднаков на односоткоефициенти на повисоки сили 
Функциски диференцијал
Функцијата се нарекува диференцијабилна во точката, ограничување за сетот Е, ако неговиот прираст е Δ ѓ(x 0), што одговара на зголемувањето на аргументот x, може да се претстави во форма
Δ ѓ(x 0) = А(x 0)(x - x 0) + ω (x - x 0), (1)
Каде ω (x - x 0) = О(x - x 0) на x → x 0 .
Приказот се нарекува диференцијалфункции ѓво точката x 0 и вредноста А(x 0)ч - диференцијална вредноство овој момент.
За функцијата диференцијална вредност ѓприфатена ознака дфили дф(x 0) ако треба да знаете во кој момент е пресметано. Така,
дф(x 0) = А(x 0)ч.
Делење во (1) со x - x 0 и насочување xНа x 0, добиваме А(x 0) = ѓ"(x 0). Затоа имаме
дф(x 0) = ѓ"(x 0)ч. (2)
Споредувајќи ги (1) и (2), гледаме дека вредноста на диференцијалот дф(x 0) (на ѓ"(x 0) ≠ 0) да главен делфункционални зголемувања ѓво точката x 0, линеарна и хомогена во исто време во однос на прирастот ч = x - x 0 .
Критериум за диференцијабилност на функција
Со цел за функцијата ѓбеше диференцијабилна во дадена точка x 0, потребно е и доволно да има конечен извод во оваа точка.
Непроменливост на формата на првиот диференцијал
Ако xе независната променлива, тогаш dx = x - x 0 (фиксен прираст). Во овој случај имаме
дф(x 0) = ѓ"(x 0)dx. (3)
Ако x = φ (т) е диференцијабилна функција, тогаш dx = φ" (т 0)dt. Оттука,
Видовме дека диференцијалот на функцијата може да се запише како:
 (1),
(1),
Ако  постои независна променлива. Нека сега
постои независна променлива. Нека сега  постои сложена функција од
постои сложена функција од  , т.е.
, т.е.  ,
, и затоа
и затоа  . Ако изводите на функциите
. Ако изводите на функциите  И
И  постои, тогаш
постои, тогаш  , како извод на сложена функција. Диференцијал
, како извод на сложена функција. Диференцијал  или. Но
или. Но  и затоа можеме да пишуваме
и затоа можеме да пишуваме  , т.е. го доби изразот за повторно
, т.е. го доби изразот за повторно  како во (1).
како во (1).
Заклучок:формулата (1) е точна како во случајот кога  постои независна променлива, така е и случајот кога
постои независна променлива, така е и случајот кога  постои функција на независната променлива
постои функција на независната променлива  . Во првиот случај, под
. Во првиот случај, под  се подразбира како диференцијал на независната променлива
се подразбира како диференцијал на независната променлива  , во втората – диференцијалот на функцијата (во овој случај
, во втората – диференцијалот на функцијата (во овој случај  , општо земено). Ова својство за зачувување на обликот (1) се нарекува непроменливост на диференцијалната форма.
, општо земено). Ова својство за зачувување на обликот (1) се нарекува непроменливост на диференцијалната форма.
Непроменливоста на диференцијалната форма дава големи придобивки при пресметување на диференцијали на сложени функции.
На пример: треба да се пресмета  . Без разлика дали променливата е зависна или независна
. Без разлика дали променливата е зависна или независна  , можеме да го запишеме. Ако
, можеме да го запишеме. Ако  - функција, на пример
- функција, на пример  , тогаш ќе најдеме
, тогаш ќе најдеме  и, користејќи ја непроменливоста на формата на диференцијалот, имаме право да пишуваме.
и, користејќи ја непроменливоста на формата на диференцијалот, имаме право да пишуваме.
§18. Деривати на повисоки нарачки.
Нека функцијата y = (x) е диференцијабилна на одреден интервал X (односно, има конечен извод y 1 = 1 (x) во секоја точка од овој интервал). Тогаш 1 (x) во самиот X е функција од x. Може да испадне дека во некои точки или воопшто x самиот 1 (x) има извод, т.е. има извод на изводот (y 1) 1 =( 1 (x) 1. Во овој случај се нарекува втор извод или извод од втор ред. Се означува со симболите y 11, 11 (x), d 2 y/ dx 2. Доколку е потребно нагласете дека изводот е во t.x 0, тогаш напишете
y 11 /x=x 0 или 11 (x 0) или d 2 y/ dx 2 /x=x 0
изводот од 1 се нарекува дериват од прв ред или прв извод.
Значи, изводот од втор ред е изводот на изводот од прв ред на функцијата.
Сосема слично, изводот (каде што постои) на извод од втор ред се нарекува дериват од трет ред или извод од трет ред.
Означи (y 11) 1 = y 111 = 111 (x)= d 3 y/ dx 3 = d 3 (x) / dx 3
Општо земено, изводот од n-ти ред на функцијата y = (x) се нарекува извод на изводот од (n-1) ред на оваа функција. (ако постојат, се разбира).
Назначи
Прочитај: n-ти извод на y, од (x); d n y од d x во n-тото.
Четврто, петто, итн. Незгодно е да се означи редоследот со потези, затоа запишете го бројот во загради, наместо v (x) напишете (5) (x).
Во загради за да не се помешаат n-тиот ред на изводот и n-тиот степен на функцијата.
Деривати од повисок ред од првиот се нарекуваат деривати од повисок ред.
Од самата дефиниција произлегува дека за да се најде n-тиот извод, треба последователно да се најдат сите претходни од 1-ви до (n-1)-ти.
Примери: 1) y=x 5; y 1 = 5x 4; y 11 = 20x 3;
y 111 = 60x 2; y (4) =120x; y (5) =120; y (6) =0,…
2) y=e x; y 1 = e x; y 11 =e x;…;
3) y=sinх; y 1 = cosх; y 11 = -sinх; y 111 = -cosх; y (4) = грев;…
Забележете дека вториот дериват има одредено механичко значење.
Ако првиот извод на патеката во однос на времето е брзината на праволиниско нерамномерно движење
V=ds/dt, каде што S=f(t) е равенката на движење, тогаш V 1 =dV/dt= d 2 S/dt 2 е брзината на промена на брзината, т.е. забрзување на движењето:
a= f 11 (t)= dV/dt= d 2 S/dt 2 .
Значи, вториот дериват на патеката во однос на времето е забрзување на движењето на точката - ова е механичкото значење на вториот дериват.
Во некои случаи, можно е да се напише израз за дериват од кој било ред, заобиколувајќи ги средните.
Примери:
y=e x; (y) (n) = (e x) (n) = e x;
y=a x; y 1 =a x lna; y 11 =a x (lna) 2; y (n) =a x (lna) n;
y=x α; y 1 = αx α-1; y 11 =  ; y (n) = α(α-1)… (α-n+1)x α-n, со
; y (n) = α(α-1)… (α-n+1)x α-n, со  =n имаме
=n имаме
y (n) = (x n) (n) = n! Деривати од ред повисок се сите еднакви на нула.
y=sinx; y 1 = cosх; y 11 = -sinх; y 111 = -cosх; y (4) = sinx;... итн.. Бидејќи
y 1 = грев (x+  /2); y 11 = грев (x+2
/2); y 11 = грев (x+2  /2); y 111 = грев (x+3
/2); y 111 = грев (x+3  /2); итн., тогаш y (n) = (sinx) (n) = sin (x + n
/2); итн., тогаш y (n) = (sinx) (n) = sin (x + n  /2).
/2).
Лесно е да се утврди со последователни диференцијации и општи формули:
1) (СU) (n) = С(U) (n) ;
2) (U±V) (n) = U (n) ± V (n)
Формулата за n-тиот извод на производот од две функции (U·V) (n) се покажува како посложена. Се нарекува формула на Лајбниц.
Ајде да го добиеме
y=U·V; y 1 = U 1 V + UV 1; y 11 = U 11 V+ U 1 V 1 + U 1 V 1 + UV 11 = U 11 V+2U 1 V 1 + UV 11;
y 111 = U 111 V+ U 11 V 1 +2U 11 V 1 +2U 1 V 11 + U 1 V 11 + UV 111 = U 111 V+3U 11 V 1 +3 U 1 V 11 + UV 111;
Слично добиваме
y (4) = U (4) V+4 U 111 V 1 +6 U 11 V 11 +4 U 1 V 111 + UV (4), итн.
Лесно е да се види дека десните страни на сите овие формули личат на проширувањето на моќите на биномот U + V, (U + V) 2, (U + V) 3, итн. Само наместо силите U и V има деривати на соодветните редови. Сличноста ќе биде особено целосна ако во добиените формули напишеме наместо U и V, U (0) и V (0), т.е. 0-ти изводи на функциите U и V (самите функции).
Проширувајќи го овој закон на случајот на кое било n, ја добиваме општата формула
y (n) = (UV) (n) = U (n) V+ n/1! U (n-1) V 1 + n(n-1)/2! U (n-2) V (2) + n(n-1) (n-2)/3! U (n-3) V (3) +…+ n(n-1)…(n-к+1)/К! U (k) V (n-k) +…+ UV (n) - формула на Лајбниц.
Пример: најдете (e x x) (n)
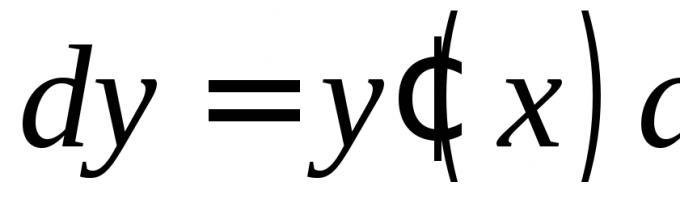
 График на функцијата
График на функцијата
 О 1
О 1