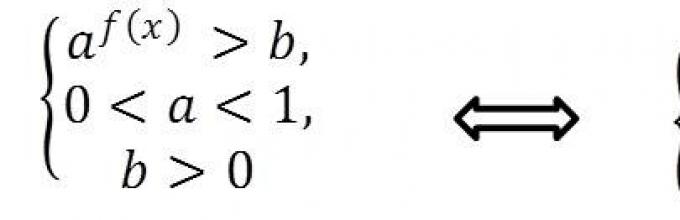Неравенството е нумеричка врска која ја илустрира големината на броевите релативно едни на други. Нееднаквостите се широко користени во потрагата по количини во применетите науки. Нашиот калкулатор ќе ви помогне да се справите со таква тешка тема како што е решавањето линеарни неравенки.
Што е нееднаквост
Нееднакви соодноси во вистински животкорелираат со постојана споредбаразни предмети: повисоки или пониски, подалеку или поблиску, потешки или полесни. Интуитивно или визуелно, можеме да разбереме дека еден предмет е поголем, повисок или потежок од друг, но всушност секогаш зборуваме за споредување на броеви кои ги карактеризираат соодветните величини. Објектите може да се споредуваат на која било основа и во секој случај можеме да создадеме нумеричка неравенка.
Ако непознатите величини се еднакви под одредени услови, тогаш создаваме равенка за да ги одредиме нумерички. Ако не, тогаш наместо знакот „еднакво“ можеме да означиме каква било друга врска помеѓу овие количини. Два броја или математички објекти можат да бидат поголеми од „>“, помали од „<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.
Знаците за нееднаквост во нивната модерна форма ги измислил британскиот математичар Томас Хариот, кој во 1631 година објавил книга за нееднакви соодноси. Знаци поголеми од „>“ и помали од „<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.
Решавање на неравенки
Неравенките, како равенките, доаѓаат во различни типови. Линеарни, квадратни, логаритамски или експоненцијални нееднакви врски се решаваат со различни методи. Сепак, без оглед на методот, секоја нееднаквост мора прво да се сведе на стандардна форма. За ова се користат идентитетски трансформации кои се идентични со модификациите на еднаквостите.
Идентични трансформации на нееднаквости
Ваквите трансформации на изразите се многу слични на равенките на духови, но тие имаат нијанси што е важно да се земат предвид при решавање на неравенки.
Првата трансформација на идентитетот е идентична со слична операција со еднаквости. Истиот број или израз со непознат x може да се додаде или одземе на двете страни на нееднаков однос, додека знакот на неравенството останува ист. Најчесто, овој метод се користи во поедноставена форма како пренос на термини на израз преку знак за неравенство со промена на знакот на бројот во спротивниот. Ова значи промена на знакот на самиот поим, односно +R кога ќе се пренесе преку кој било знак за нееднаквост ќе се промени во – R и обратно.
Втората трансформација има две точки:
- На двете страни на нееднаков однос им е дозволено да се множат или делат со истиот позитивен број. Знакот на самата нееднаквост нема да се промени.
- Двете страни на неравенката може да се поделат или помножат со иста работа негативен број. Самиот знак на нееднаквост ќе се промени во спротивното.
Втората идентична трансформација на неравенките има сериозни разлики со модификацијата на равенките. Прво, при множење/делење со негативен број, знакот на нееднаков израз е секогаш обратен. Второ, можете само да делите или множите делови од односот со број, а не со кој било израз што содржи непозната. Факт е дека не можеме со сигурност да знаеме дали некој број е поголем или помал од нула скриен зад непознатото, па втората идентитетска трансформација се применува на неравенки исклучиво со броеви. Ајде да ги погледнеме овие правила со примери.
Примери за ослободување на нееднаквости
Во алгебарските задачи има најразлични задачи на тема неравенки. Да ни се даде изразот:
6x − 3(4x + 1) > 6.
Прво, да ги отвориме заградите и да ги преместиме сите непознати налево, а сите броеви надесно.
6x − 12x > 6 + 3
Треба да ги поделиме двете страни на изразот со −6, па кога ќе ја најдеме непознатата x, знакот за неравенство ќе се промени во спротивен.
При решавањето на оваа нееднаквост ги користевме и двете идентитетски трансформации: Поместете ги сите броеви десно од знакот и поделете ги двете страни на односот со негативниот број.
Нашата програма е калкулатор за решавање на нумерички неравенки кои не содржат непознати. Програмата ги содржи следните теореми за врските на три броја:
- ако< B то A–C< B–C;
- ако A > B, тогаш A–C > B–C.
Наместо да ги одземате поимите A-C, можете да наведете која било аритметичка операција: собирање, множење или делење. На овој начин, калкулаторот автоматски ќе прикаже неравенки за збирови, разлики, производи или дропки.
Заклучок
Во реалниот живот, нееднаквостите се вообичаени како равенките. Нормално, знаењето за решавање на нееднаквостите можеби не е потребно во секојдневниот живот. Меѓутоа, во применетите науки, нееднаквостите и нивните системи се широко користени. На пример, различни студии за проблемите на глобалната економија се сведуваат на компилација и раздвојување на системи на линеарни или квадратни неравенки, а некои нееднакви односи служат како недвосмислен начин за докажување на постоењето на одредени предмети. Користете ги нашите програми за решавање на линеарни неравенки или проверете ги вашите сопствени пресметки.
Здраво! Драги мои студенти, во оваа статија ќе научиме како да решаваме експоненцијални неравенки .
Колку и да ви изгледа комплицирана експоненцијалната неравенка, по некои трансформации (за нив ќе зборуваме малку подоцна) сите неравенки се сведуваат на решавање на наједноставното експоненцијални неравенки :
a x > b, а x< b И a x ≥ b, a x ≤ b.
Ајде да се обидеме да откриеме како се решаваат таквите нееднаквости.
Ќе бараме решение строги нееднаквости. Единствената разлика при решавање на нестроги неравенки е тоа што добиените соодветни корени се вклучени во одговорот.
Да претпоставиме дека треба да решиме неравенство на формата и f (x) > b, Каде а> 1И б>0.
Погледнете го дијаграмот за решавање на такви неравенки (Слика 1):
Сега да погледнеме конкретен пример. Решете неравенство: 5 x – 1 > 125.
Од 5 > 1 и 125 > 0, тогаш
x – 1 > log 5 125, т.е
x – 1 > 3,
x > 4.
Одговор: (4; +∞) .
Кое ќе биде решението за истата нееднаквост? и f (x) >b, Ако 0
Значи, дијаграмот на Слика 2

Пример: Решете ја нееднаквоста (1/2) 2x - 2 ≥ 4
Применувајќи го правилото (слика 2), добиваме
2х – 2 ≤ дневник 1/2 4,
2х – 2 ≤ –2,
2x ≤ 0,
x ≤ 0.
Одговор: (–∞; 0] .
Ајде повторно да ја погледнеме истата нееднаквост и f (x) > b, Ако a>0И б<0 .
Значи, дијаграмот на Слика 3:

Пример за решавање на неравенство (1/3) x + 2 > -9. Како што забележуваме, без разлика кој број ќе го замениме x, (1/3) x + 2 е секогаш поголем од нула.
Одговор: (–∞; +∞) .
Како се решаваат неравенките на формата? и f(x)< b , Каде а> 1И б>0?
Дијаграм на Слика 4:

И следниот пример: 3 3 – x ≥ 8.
Од 3 > 1 и 8 > 0, тогаш
3 – x > log 3 8, т.е
–x > дневник 3 8 – 3,
X< 3 – log
3 8.
Одговор: (0; 3-лог 3 8) .
Како може да се промени решението на нееднаквоста? и f(x)< b
, во 0
Дијаграм на слика 5:

И следниот пример: Решете неравенство 0,6 2x – 3< 0,36 .
Следејќи го дијаграмот на Слика 5, добиваме
2x – 3 > дневник 0,6 0,36,
2х – 3 > 2,
2x > 5,
x > 2,5
Одговор: (2,5; +∞) .
Да ја разгледаме последната шема за решавање на нееднаквост на формата и f(x)< b , во a>0И б<0 , претставено на Слика 6:

На пример, да ја решиме нееднаквоста:

Забележуваме дека без разлика кој број ќе го замениме x, левата страна на неравенката е секогаш поголема од нула, а нашиот израз е помал од -8, т.е. и нула, што значи дека нема решенија.
Одговор: нема решенија.
Знаејќи како да ги решите наједноставните експоненцијални неравенки, можете да продолжите решавање на експоненцијални неравенки.
Пример 1.
Најдете ја најголемата цел бројна вредност на x што ја задоволува неравенката

Бидејќи 6 x е поголемо од нула (на ниту еден x именителот оди на нула), множејќи ги двете страни на неравенката со 6 x, добиваме:
440 – 2 6 2x > 8, тогаш
– 2 6 2x > 8 – 440,
– 2 6 2х > – 332,
6 2x< 216,
2x< 3,
x< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.
Одговор: 1.
Пример 2.
Решете ја нееднаквоста 2 2 x – 3 2 x + 2 ≤ 0
Да означиме 2 x со y, да ја добиеме неравенката y 2 – 3y + 2 ≤ 0 и да ја решиме оваа квадратна неравенка.
y 2 – 3y +2 = 0,
y 1 = 1 и y 2 = 2.
Гранките на параболата се насочени нагоре, ајде да нацртаме график:

Тогаш решението на неравенката ќе биде неравенка 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.
Одговор: (0; 1) .
Пример 3. Решете ја нееднаквоста 5 x +1 – 3 x +2< 2·5 x – 2·3 x –1
Да собереме изрази со исти основи во еден дел од неравенката
5 x +1 – 2 5 x< 3 x +2 – 2·3 x –1
Да извадиме 5 x од заградите на левата страна на неравенката и 3 x од десната страна на неравенката и ја добиваме неравенката
5 x (5 - 2)< 3 х (9 – 2/3),
3,5 x< (25/3)·3 х
Поделете ги двете страни на неравенката со изразот 3 3 x, знакот за неравенство не се менува, бидејќи 3 3 x е позитивен број, ја добиваме неравенката:


X< 2 (так как 5/3 > 1).
Одговор: (–∞; 2) .
Ако имате прашања за решавање на експоненцијални неравенки или сакате да вежбате да решавате слични примери, пријавете се за моите лекции. Тутор Валентина Галиневскаја.
веб-страница, при копирање на материјал во целост или делумно, потребна е врска до изворот.
Метод на интервал– едноставен начин за решавање на дробни рационални неравенки. Ова е името за неравенки кои содржат рационални (или фракционо-рационални) изрази кои зависат од променлива.
1. Размислете за, на пример, следнава нееднаквост
Методот на интервал ви овозможува да го решите за неколку минути.
На левата страна на оваа нееднаквост - фракциона рационална функција. Рационално затоа што не содржи корени, нема синуси, нема логаритми - само рационални изрази. На десната страна е нула.
Методот на интервал се заснова на следново својство на фракциона рационална функција.
Дробната рационална функција може да го промени знакот само во оние точки во кои е еднаква на нула или не постои.
Дозволете ни да ве потсетиме како да се факторизира квадратен трином, односно израз на формата .
Каде и се корените квадратна равенка.
Цртаме оска и ги поставуваме точките во кои броителот и именителот одат на нула.

Нулите на именителот и се пробиени точки, бидејќи во овие точки функцијата од левата страна на неравенката не е дефинирана (не можете да ја поделите со нула). Нулите на броителот и - се засенчени, бидејќи неравенството не е строга. Кога и нашата нееднаквост е задоволена, бидејќи и двете негови страни се еднакви на нула.
Овие точки ја кршат оската во интервали.
Дозволете ни да го одредиме знакот на фракционата рационална функција на левата страна на нашата неравенка на секој од овие интервали. Се сеќаваме дека фракционата рационална функција може да го промени знакот само во оние точки во кои е еднаква на нула или не постои. Ова значи дека во секој од интервалите помеѓу точките каде што броителот или именителот оди на нула, знакот на изразот од левата страна на неравенката ќе биде константен - или „плус“ или „минус“.
И затоа, за да го одредиме знакот на функцијата на секој таков интервал, земаме која било точка што припаѓа на овој интервал. Онаа што ни е погодна.
. Земете, на пример, и проверете го знакот на изразот од левата страна на неравенката. Секоја од „заградите“ е негативна. Левата страна има знак.

Следен интервал: . Ајде да го провериме знакот на. Откриваме дека левата страна го сменила својот знак во .

Ајде да го земеме. Кога изразот е позитивен - значи, тој е позитивен во текот на целиот интервал од до.

Кога левата страна на неравенката е негативна.

И конечно, class="tex" alt="x>7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Откривме во кои интервали изразот е позитивен. Останува само да се запише одговорот:
Одговор:.
Ве молиме имајте предвид: знаците наизменично се менуваат помеѓу интервали. Ова се случи затоа што при минување низ секоја точка, точно еден од линеарните фактори го сменил знакот, додека останатите го задржале непроменет.
Гледаме дека методот на интервал е многу едноставен. За да ја решиме фракционо-рационалната нееднаквост користејќи го методот на интервал, ја сведуваме на формата:
Или class="tex" alt="\genfrac())()(0)(\displaystyle P\left(x \десно))(\displaystyle Q\left(x \десно)) > 0"> !}, или или .
(на левата страна е фракциона рационална функција, на десната страна е нула).
Потоа на бројната права ги означуваме точките на кои броителот или именителот оди на нула.
Овие точки ја делат целата бројна права на интервали, на секој од нив фракционо-рационалната функција го задржува својот знак.
Останува само да се дознае неговиот знак на секој интервал.
Ова го правиме со проверка на знакот на изразот во која било точка што припаѓа на даден интервал. После тоа, го запишуваме одговорот. Тоа е се.
Но, се поставува прашањето: дали знаците секогаш се менуваат? Не, не секогаш! Мора да бидете внимателни и да не поставувате знаци механички и непромислено.
2. Да разгледаме уште една нееднаквост.
Class="tex" alt="\genfrac())()(0)(\displaystyle \left(x-2 \десно)^2)(\displaystyle \left(x-1 \десно) \ лево(x-3 \десно))>0"> !}
Поставете ги точките на оската повторно. Точките и се пробиени бидејќи се нули од именителот. Поентата е исто така отсечена, бидејќи нееднаквоста е строга.

Кога броителот е позитивен, двата фактора во именителот се негативни. Ова може лесно да се провери со земање на кој било број од даден интервал, на пример, . Левата страна го има знакот:

Кога броителот е позитивен; Првиот фактор во именителот е позитивен, вториот фактор е негативен. Левата страна го има знакот:

Ситуацијата е иста! Броителот е позитивен, првиот фактор во именителот е позитивен, вториот е негативен. Левата страна го има знакот:

Конечно, со class="tex" alt="x>3">
все множители положительны, и левая часть имеет знак :!} 
Одговор:.
Зошто беше нарушена алтернацијата на знаците? Затоа што кога поминува низ точка множителот е „одговорен“ за тоа не го смени знакот. Следствено, целата лева страна на нашата нееднаквост не го смени знакот.
Заклучок: ако линеарниот множител е парна моќност (на пример, квадрат), тогаш при минување низ точка знакот на изразот од левата страна не се менува. Во случај на непарен степен, знакот, се разбира, се менува.
3. Ајде да размислиме повеќе тежок случај. Се разликува од претходната по тоа што нееднаквоста не е строга:
Левата страна е иста како и во претходниот проблем. Сликата на знаците ќе биде иста:

Можеби одговорот ќе биде ист? Не! Се додава решение Ова се случува затоа што и на левата и на десната страна на неравенката се еднакви на нула - затоа, оваа точка е решение.
Одговор:.
Оваа ситуација често се јавува во проблеми на обединетиот државен испит по математика. Ова е местото каде што апликантите паѓаат во стапица и губат поени. Внимавај!
4. Што да направите ако броителот или именителот не може да се разложат на линеарни фактори? Размислете за оваа нееднаквост:
Квадратен трином не може да се факторизира: дискриминантот е негативен, нема корени. Но, ова е добро! Тоа значи дека знакот на изразот за сите е ист, а конкретно позитивен. Можете да прочитате повеќе за ова во написот за својствата на квадратните функции.
И сега можеме да ги поделиме двете страни на нашата нееднаквост со вредност која е позитивна за сите. Да дојдеме до еквивалентна неравенка:
Што лесно се решава со методот на интервал.
Ве молиме имајте предвид дека ги поделивме двете страни на нееднаквоста со вредност за која сигурно знаевме дека е позитивна. Се разбира, генерално, не треба да множите или делите неравенство со променлива чиј знак е непознат.
5 . Да разгледаме уште една нееднаквост, навидум прилично едноставна:
Сакам само да го помножам со. Но, ние сме веќе паметни и нема да го сториме тоа. На крајот на краиштата, тоа може да биде и позитивно и негативно. И знаеме дека ако двете страни на нееднаквоста се помножат со негативна вредност, знакот на нееднаквоста се менува.
Ќе го направиме тоа поинаку - ќе собереме сè во еден дел и ќе го доведеме до заеднички именител. Десната страна ќе остане нула:
Class="tex" alt="\genfrac())()()(0)(\displaystyle x-2)(\displaystyle x)>0"> !}
И после тоа - аплицирајте метод на интервал.
На пример, неравенката е изразот \(x>5\).
Видови неравенки:
Ако \(a\) и \(b\) се броеви или , тогаш се повикува неравенството нумерички. Тоа е всушност само споредување на два броја. Ваквите нееднаквости се поделени на веренИ неверен.
На пример:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);
\(17+3\geq 115\) е неточна нумеричка неравенка, бидејќи \(17+3=20\), а \(20\) е помало од \(115\) (и не поголемо или еднакво на) .
Ако \(a\) и \(b\) се изрази што содржат променлива, тогаш имаме нееднаквост со променлива. Ваквите нееднаквости се поделени на типови во зависност од содржината:
|
\(2x+1\geq4(5-x)\) |
Променлива само до првата моќност |
|||
|
\(3x^2-x+5>0\) |
Има променлива во втората моќност (квадрат), но нема повисоки сили (трета, четврта, итн.) |
|||
|
\(\log_(4)((x+1))<3\) |
||||
|
\(2^(x)\leq8^(5x-2)\) |
Кое е решението за нееднаквоста?
Ако замените број наместо променлива со неравенка, тој ќе се претвори во нумеричка.
Ако дадена вредност за x ја претвори оригиналната неравенка во вистинска нумеричка, тогаш таа се нарекува решение за нееднаквоста. Ако не, тогаш оваа вредност не е решение. И да реши нееднаквост– треба да ги најдете сите негови решенија (или да покажете дека ги нема).
На пример,ако го замениме бројот \(7\) во линеарната неравенка \(x+6>10\), ја добиваме точната бројна неравенка: \(13>10\). И ако го замениме \(2\), ќе има неточна бројна неравенка \(8>10\). Односно, \(7\) е решение за првичната неравенка, но \(2\) не е.
Меѓутоа, неравенката \(x+6>10\) има други решенија. Навистина, ќе ги добиеме точните нумерички неравенки при замена на \(5\), и \(12\), и \(138\)... И како можеме да ги најдеме сите можни решенија? За ова тие користат За нашиот случај имаме:
\(x+6>10\) \(|-6\)
\(x>4\)
Односно, секој број поголем од четири е погоден за нас. Сега треба да го запишете одговорот. Решенијата на неравенките обично се пишуваат нумерички, дополнително означувајќи ги на бројната оска со засенчување. За нашиот случај имаме:
Одговор:
\(x\in(4;+\infty)\)
Кога се менува знакот на нееднаквост?
Постои една голема замка во нееднаквостите во кои студентите навистина „сакаат“ да паднат:
При множење (или делење) на неравенство со негативен број, тој се менува („повеќе“ со „помалку“, „повеќе или еднакво“ со „помалку или еднакво“ и така натаму)
Зошто се случува ова? За да го разбереме ова, да ги погледнеме трансформациите нумеричка неравенка\(3>1\). Точно е, три се навистина поголеми од едно. Прво, да се обидеме да го помножиме со кој било позитивен број, на пример, два:
\(3>1\) \(|\cdot2\)
\(6>2\)
Како што можеме да видиме, по множењето неравенството останува точно. И без разлика со кој позитивен број ќе помножиме, секогаш ќе ја добиеме точната неравенка. Сега да се обидеме да помножиме со негативен број, на пример, минус три:
\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)
Резултатот е неточна неравенка, бидејќи минус девет е помал од минус три! Тоа е, за да може нееднаквоста да стане вистинита (и затоа, трансформацијата на множењето со негативно беше „правна“), треба да го смените знакот за споредба, вака: \(-9<− 3\).
Со делење ќе функционира на ист начин, можете сами да го проверите.
Правилото напишано погоре важи за сите видови неравенки, а не само за нумеричките.
Пример: Решете ја неравенката \(2(x+1)-1<7+8x\)Решение:
|
\(2x+2-1<7+8x\) |
Ајде да се движиме \(8x\) налево, и \(2\) и \(-1\) надесно, не заборавајќи да ги смениме знаците |
|
\(2x-8x<7-2+1\) |
|
|
\(-6x<6\) \(|:(-6)\) |
Ајде да ги поделиме двете страни на нееднаквоста со \(-6\), не заборавајќи да се смениме од „помалку“ во „повеќе“ |
|
Да означиме нумерички интервал на оската. Нееднаквост, затоа ја „избодуваме“ самата вредност \(-1\) и не ја земаме како одговор |
|
|
Ајде да го напишеме одговорот како интервал |
Одговор: \(x\in(-1;\infty)\)
Нееднаквости и попреченост
Неравенките, исто како равенките, можат да имаат ограничувања на , односно на вредностите на x. Соодветно на тоа, оние вредности што се неприфатливи според DZ треба да бидат исклучени од опсегот на решенија.
Пример: Решете ја неравенката \(\sqrt(x+1)<3\)
Решение: Јасно е дека за левата страна да биде помала од \(3\), радикалниот израз мора да биде помал од \(9\) (на крајот на краиштата, од \(9\) само \(3\)). Добиваме:
\(x+1<9\) \(|-1\)
\(х<8\)
Сите? Дали ќе ни одговара некоја вредност од x помала од \(8\)? Не! Затоа што ако ја земеме, на пример, вредноста \(-5\) што се чини дека одговара на барањето, тоа нема да биде решение за првобитната неравенка, бидејќи ќе не доведе до пресметување на коренот на негативен број.
\(\sqrt(-5+1)<3\)
\(\sqrt(-4)<3\)
Затоа, мора да ги земеме предвид и ограничувањата на вредноста на X - не може да биде таква што има негативен број под коренот. Така, го имаме второто барање за x:
\(x+1\geq0\)
\(x\geq-1\)
А за x да биде конечно решение, мора да ги задоволува двете барања одеднаш: мора да биде помало од \(8\) (да биде решение) и поголемо од \(-1\) (да биде во принцип прифатливо). Исцртувајќи го на бројната линија, го имаме конечниот одговор:

Одговор: \(\лево[-1;8\десно)\)
Внимание!
Има дополнителни
материјали во Посебен дел 555.
За оние кои се многу „не многу...“
И за оние кои „многу...“)
Што се случи „квадратна нееднаквост“?Без прашање!) Ако земете било којквадратна равенка и заменете го знакот во неа "=" (еднакво) на кој било знак за нееднаквост ( > ≥ < ≤ ≠ ), добиваме квадратна неравенка. На пример:
1. x 2 -8x+12 ≥ 0
2. -x 2 +3x > 0
3. x 2 ≤ 4
Па, разбираш...)
Не за џабе ги поврзав равенките и неравенките овде. Поентата е дека првиот чекор во решавањето било којквадратна нееднаквост - реши ја равенката од која е направена оваа неравенка.Поради оваа причина, неможноста да се решат квадратните равенки автоматски доведува до целосен неуспех во неравенките. Дали е јасен навестувањето?) Ако има нешто, погледнете како да ги решите сите квадратни равенки. Сè е опишано таму во детали. И во оваа лекција ќе се занимаваме со нееднаквости.
Неравенката подготвена за решение има форма: лево е квадратен трином секира 2 +bx+c, од десната страна - нула.Знакот за нееднаквост може да биде апсолутно сè. Првите два примери се тука веќе се подготвени да донесат одлука.Третиот пример допрва треба да се подготви.
Доколку ви се допаѓа оваа страница...
Патем, имам уште неколку интересни страници за вас.)
Можете да вежбате да решавате примери и да го дознаете вашето ниво. Тестирање со инстант верификација. Ајде да научиме - со интерес!)
Можете да се запознаете со функции и деривати.