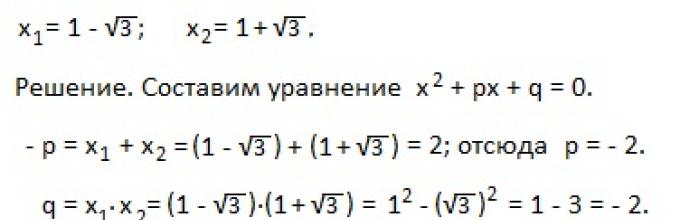Во првата изјава се наведува дека збирот на корените на оваа равенка е еднаков на вредноста на коефициентот на променливата x (во овој случај тоа е b), но со спротивен знак. Визуелно изгледа вака: x1 + x2 = −b.
Вториот исказ повеќе не е поврзан со збирот, туку со производот на истите два корени. Овој производ е изедначен со слободниот коефициент, т.е. в. Или, x1 * x2 = c. И двата примери се решени во системот.
Теоремата на Виета во голема мера го поедноставува решението, но има едно ограничување. Квадратна равенка чии корени можат да се најдат со помош на оваа техника мора да се намали. Во горната равенка, коефициентот a, оној пред x2, е еднаков на еден. Секоја равенка може да се доведе до слична форма со делење на изразот со првиот коефициент, но оваа операција не е секогаш рационална.
Доказ за теоремата
За почеток, треба да се потсетиме како, според традицијата, вообичаено е да се бараат корени квадратна равенка. Најдени се првиот и вториот корен и тоа: x1 = (-b-√D)/2, x2 = (-b+√D)/2. Во принцип, таа е делива со 2а, но, како што веќе беше споменато, теоремата може да се примени само кога a=1.Од теоремата на Виета се знае дека збирот на корените е еднаков на вториот коефициент со знак минус. Ова значи дека x1 + x2 = (-b-√D)/2 + (-b+√D)/2 = −2b/2 = −b.
Истото важи и за производот на непознати корени: x1 * x2 = (-b-√D)/2 * (-b+√D)/2 = (b2-D)/4. За возврат, D = b2-4c (повторно со a=1). Излегува дека резултатот е: x1 * x2 = (b2- b2)/4+c = c.
Од горенаведеното едноставен доказМоже да се извлече само еден заклучок: теоремата на Виета е целосно потврдена.
Втора формулација и доказ
Теоремата на Виета има друга интерпретација. Да бидам попрецизен, тоа не е толкување, туку формулација. Факт е дека ако се исполнети истите услови како во првиот случај: постојат два различни реални корени, тогаш теоремата може да се напише со друга формула.Оваа еднаквост изгледа вака: x2 + bx + c = (x - x1) (x - x2). Ако функцијата P(x) се вкрстува во две точки x1 и x2, тогаш може да се запише како P(x) = (x - x1)(x - x2) * R(x). Во случај кога P има втор степен, а токму вака изгледа оригиналниот израз, тогаш R е прост број, имено 1. Оваа изјава е точна од причина што во спротивно еднаквоста нема да важи. Коефициентот x2 при отворање на заградите не треба да биде поголем од еден, а изразот треба да остане квадрат.
Три броја 12x, x 2-5 и 4 по тој редослед формираат растечки аритметичка прогресија https://youtu.be/U0VO_N9udpIИзберете ја точната изјава МАТЕМАТИКА ЗФТШ МИПТ Московски институт за физика и технологија ( државен универзитет) Кореспонденција физичко и техничко училиште. http://pin.it/9w-GqGpНајдете ги сите x, y и z така што броевите 5x + 3, y2 и 3z + 5 да формираат аритметичка прогресија по тој редослед. Најдете x и означете ја разликата на оваа прогресија. Решете го системот на равенки Единствен државен испит по математика. Видео упатства. Деливост на цели броеви. Линеарна функција. Проблеми со деливост. Теорема на Виета, конверзна теорема, формули на Виета. паметен #студенти #равенки #vietas_теорема #теоремаСледно, ја разгледуваме теоремата обратна на теоремата на Виета. По ова, ќе ги анализираме решенијата на најтипичните примери. Ова ја докажува првата релација на теоремата на Виета за збирот на корените на квадратна равенка. Да преминеме на второто. Како да се докаже обратната страна на теоремата на Виета? DOK-VO: x2+px+f=0 x2-(M+N) *x+M*N=0 x2-Mx-Nx+M*N=0 x (x-N) -M (x-N) =0 (x-M ) (x-N) =0 x-M=0 x-N=0 x=M x=N CTD. Вака го докажавме тоа класа на профилсо математичка пристрасност. Одговори: помогне да се разбере теоремата инверзна на теоремата на Виета благодарение на конкретни примери Теоремата инверзна на теоремата на Виета помага да се реши решението: Ако коефициентот a е број од кој лесно се извлекува квадратен коренцелината рационален број, тогаш збирот на x1 и x2 ќе биде еднаков на бројот. Формулирајте и докажете ја теоремата на Виета, како и обратната теорема и применете ги теоремите за решавање равенки и проблеми. Докажете ја обратната страна на теоремата на Виета. Единствен државен испит по математика за 100 поени: тајни за кои не се зборува училишни наставници, проблеми со деривати. Многу апликанти мислат дека не треба да се подготвуваат за првите четиринаесет проблеми, мислејќи дека се многу лесни, но тоа не е така! Повеќето испитувачи прават едноставни аритметички грешки, а со тоа го заматуваат одлично решениепроблеми од дел В. Ваквите ситуации се случуваат многу често, затоа, нема потреба да се занемарува подготовката за првите задачи, туку подгответе се како на спортски тренинг: ако се стремите кон 90-100 поени, вежбајте да го решавате првиот блок во 20-25 минути, ако за 70 -80 поени – околу 30 минути, не повеќе. Одличен начин да се тренирате е да решавате во друштво на тутор, на курсеви каде ќе бидат поставени одредени услови: на пример, решавате пред првата грешка, а потоа ја предавате работата; Друга опција е за секоја грешка да донирате пари на општата каса. Колку и да изгледа чудно, не ја препорачуваме официјалната веб-страница, бидејќи сите тестови таму се толку измешани што е невозможно да се користи. Форматирањето на задачите од Дел В е важно. Ако решението не се подготви внимателно, тогаш напредокот во решавањето на задачата ќе биде нејасен, и затоа, испитувачот дефинитивно ќе најде грешка во ова и ќе го намали вашиот резултат. Се чини дека зборувавме за многу едноставни работи, но следејќи ги нашите совети, ќе си обезбедите успех полагање на Единствен државен испит! Тајните врски за кои се дискутираше во Мастер класата може да се најдат овде - ова се линкови до видео курсеви за подготовка за обединет државен испит. Добиениот резултат се нарекува теорема на Виета. За даденото квадратен трином 2 x px q Теоремата на Виета изгледа вака: ако има корени, тогаш важи и инверзната на теоремата на Виета: ако броевите ги задоволуваат условите, тогаш овие броеви се корените на равенката. Доказот за оваа теорема е еден од прашања за тестирањеЗадачи. Понекогаш, за краткост, двете теореми на Виета (директни и инверзни) едноставно се нарекуваат теорема на Виета.
I. Теорема на Виетаза намалената квадратна равенка.
Збир на корените на намалената квадратна равенка x 2 +px+q=0е еднаков на вториот коефициент земен со спротивен знак, а производот на корените е еднаков на слободниот член:
x 1 + x 2 = -p; x 1 ∙x 2 =q.
Најдете ги корените на дадената квадратна равенка користејќи ја теоремата на Виета.
Пример 1) x 2 -x-30=0.Ова е намалената квадратна равенка ( x 2 +px+q=0), втор коефициент p=-1, А слободен член q=-30.Прво, да се увериме дека оваа равенка има корени и дека корените (ако ги има) ќе бидат изразени во цели броеви. За ова доволно е дискриминаторот да биде совршен квадратцел број.
Наоѓање на дискриминаторот Д=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121= 11 2 .
Сега, според теоремата на Виета, збирот на корените мора да биде еднаков на вториот коефициент земен со спротивниот знак, т.е. ( -стр), а производот е еднаков на слободниот член, т.е. ( q). Потоа:
x 1 + x 2 =1; x 1 ∙x 2 =-30.Треба да избереме два броја такви што нивниот производ е еднаков на -30 , а износот е единица. Ова се бројки -5 И 6 . Одговор: -5; 6.
Пример 2) x 2 +6x+8=0.Намалената квадратна равенка ја имаме со вториот коефициент p=6и слободен член q=8. Ајде да се увериме дека има целобројни корени. Да го најдеме дискриминаторот Д 1 Д 1=3 2 -1∙8=9-8=1=1 2 . Дискриминантната D 1 е совршен квадрат на бројот 1 , што значи дека корените на оваа равенка се цели броеви. Дозволете ни да ги избереме корените користејќи ја теоремата на Виета: збирот на корените е еднаков на –р=-6, а производот на корените е еднаков на q=8. Ова се бројки -4 И -2 .
Всушност: -4-2=-6=-р; -4∙(-2)=8=q. Одговор: -4; -2.
Пример 3) x 2 +2x-4=0. Во оваа намалена квадратна равенка, вториот коефициент p=2, и слободниот член q=-4. Да го најдеме дискриминаторот Д 1, бидејќи вториот коефициент е парен број. Д 1=1 2 -1∙(-4)=1+4=5. Дискриминаторот не е совршен квадрат од бројот, така што и ние заклучок: Корените на оваа равенка не се цели броеви и не можат да се најдат со помош на теоремата на Виета.Ова значи дека ја решаваме оваа равенка, како и обично, користејќи формули (во овој случај, користејќи формули). Добиваме:
Пример 4).Напишете квадратна равенка користејќи ги нејзините корени ако x 1 =-7, x 2 =4.
Решение.Потребната равенка ќе биде напишана во форма: x 2 +px+q=0, и, врз основа на теоремата на Виета –p=x 1 +x 2=-7+4=-3 → p=3; q=x 1 ∙x 2=-7∙4=-28 . Тогаш равенката ќе ја добие формата: x 2 +3x-28=0.
Пример 5).Напишете квадратна равенка користејќи ги нејзините корени ако:

II. Теорема на Виетаза целосна квадратна равенка секира 2 +bx+c=0.
Збирот на корените е минус б, поделено со А, производот на корените е еднаков на Со, поделено со А:
x 1 + x 2 = -b/a; x 1 ∙x 2 =c/a.
Пример 6).Најдете го збирот на корените на квадратна равенка 2x 2 -7x-11=0.
Еден од методите за решавање на квадратна равенка е да се користи VIET формули, кој го добил името по ФРАНСОА ВИЕТЕ.
Тој бил познат адвокат кој му служел на францускиот крал во 16 век. ВО слободно времестудирал астрономија и математика. Тој воспоставил врска помеѓу корените и коефициентите на квадратната равенка.
Предности на формулата:
1 . Со примена на формулата, можете брзо да најдете решение. Затоа што нема потреба да се внесува вториот коефициент во квадрат, потоа да се одземе 4ac од него, да се најде дискриминаторот и да се замени неговата вредност во формулата за да се најдат корените.
2 . Без решение, можете да ги одредите знаците на корените и да ги изберете вредностите на корените.
3 . Откако решивме систем од два записи, не е тешко да се најдат самите корени. Во горната квадратна равенка, збирот на корените е еднаков на вредноста на вториот коефициент со знак минус. Производот на корените во горната квадратна равенка е еднаков на вредноста на третиот коефициент.
4 . Користејќи ги овие корени, запишете квадратна равенка, односно решете ја инверзната задача. На пример, овој метод се користи при решавање на проблеми во теоретската механика.
5 . Удобно е да се користи формулата кога водечкиот коефициент е еднаков на еден.
Недостатоци:
1
. Формулата не е универзална.
Теорема на Виета 8 одделение
Формула
Ако x 1 и x 2 се корените на намалената квадратна равенка x 2 + px + q = 0, тогаш:

Примери
x 1 = -1; x 2 = 3 - корени на равенката x 2 - 2x - 3 = 0.
P = -2, q = -3.
X 1 + x 2 = -1 + 3 = 2 = -p,
X 1 x 2 = -1 3 = -3 = q.
Конверзна теорема
Формула
Ако броевите x 1, x 2, p, q се поврзани со условите:

Тогаш x 1 и x 2 се корените на равенката x 2 + px + q = 0.
Пример
Ајде да создадеме квадратна равенка користејќи ги нејзините корени:
X 1 = 2 - ? 3 и x 2 = 2 + ? 3.
P = x 1 + x 2 = 4; p = -4; q = x 1 x 2 = (2 - ? 3 ) (2 + ? 3 ) = 4 - 3 = 1.
Потребната равенка има форма: x 2 - 4x + 1 = 0.
Помеѓу корените и коефициентите на квадратната равенка, покрај коренските формули, постојат и други корисни врски кои се дадени Теорема на Виета. Во оваа статија ќе дадеме формулација и доказ за теоремата на Виета за квадратна равенка. Следно, ја разгледуваме теоремата обратна на теоремата на Виета. По ова, ќе ги анализираме решенијата на најтипичните примери. Конечно, ги запишуваме формулите Vieta кои ја дефинираат врската помеѓу вистинските корени алгебарска равенка степенот n и неговите коефициенти.
Навигација на страница.
Теорема на Виета, формулација, доказ
Од формулите за корените на квадратната равенка a·x 2 +b·x+c=0 од формата, каде што D=b 2 −4·a·c следуваат следните односи: x 1 +x 2 =− b/a, x 1 ·x 2 = c/a . Овие резултати се потврдени Теорема на Виета:
Теорема.
Ако x 1 и x 2 се корените на квадратната равенка a x 2 +b x+c=0, тогаш збирот на корените е еднаков на односот на коефициентите b и a, земени со спротивен знак, а производот од корените се еднакви на односот на коефициентите c и a, односно .
Доказ.
Доказот на теоремата на Виета ќе го извршиме според следната шема: ќе го составиме збирот и производот од корените на квадратната равенка користејќи познати коренски формули, потоа ќе ги трансформираме добиените изрази и ќе се увериме дека тие се еднакви на − b/a и c/a, соодветно.
Да почнеме со збирот на корените и да го составиме. Сега ги доведуваме дропките до заеднички именител, имаме . Во броителот на добиената дропка, по што:. Конечно, по 2, добиваме . Ова ја докажува првата релација на теоремата на Виета за збирот на корените на квадратна равенка. Да преминеме на второто.
Го составуваме производот од корените на квадратната равенка: . Според правилото за множење дропки, последно парчеможе да се напише како . Сега множиме заграда со заграда во броителот, но побрзо е да се склопи овој производ со формула за квадратна разлика, Значи. Потоа, сеќавајќи се, ја извршуваме следната транзиција. И бидејќи дискриминантата на квадратната равенка одговара на формулата D=b 2 −4·a·c, тогаш наместо D во последната дропка можеме да го замениме b 2 −4·a·c, добиваме. По отворањето на заградите и леењето слични терминидоаѓаме до дропката , а нејзиното намалување за 4·a дава . Ова ја докажува втората релација на теоремата на Виета за производот на корените.
Ако ги испуштиме објаснувањата, доказот на теоремата на Виета ќе има лаконска форма:
,
.
Останува само да се забележи дека ако дискриминаторот е еднаков на нула, квадратната равенка има еден корен. Меѓутоа, ако претпоставиме дека равенката во овој случај има два идентични корени, тогаш важат и еднаквостите од теоремата на Виета. Навистина, кога D=0 коренот на квадратната равенка е еднаков на , тогаш и , и бидејќи D=0, односно b 2 −4·a·c=0, од каде b 2 =4·a·c, тогаш .
Во пракса, теоремата на Виета најчесто се користи во однос на намалената квадратна равенка (со водечки коефициент a еднаков на 1) од формата x 2 +p·x+q=0. Понекогаш се формулира за квадратни равенки токму од овој тип, што не ја ограничува општоста, бидејќи секоја квадратна равенка може да се замени со еквивалентна равенка со делење на двете страни со ненула број a. Да ја дадеме соодветната формулација на теоремата на Виета:
Теорема.
Збирот на корените на намалената квадратна равенка x 2 +p x+q=0 е еднаков на коефициентот x земен со спротивен знак, а производот на корените е еднаков на слободниот член, односно x 1 +x 2 =−p, x 1 x 2 = q.
Теоремата е во спротивност со теоремата на Виета
Втората формулација на теоремата на Виета, дадена во претходниот пасус, покажува дека ако x 1 и x 2 се корените на намалената квадратна равенка x 2 +p x+q=0, тогаш односите x 1 +x 2 =−p , x 1 x 2 =q. Од друга страна, од напишаните релации x 1 +x 2 =−p, x 1 x 2 =q произлегува дека x 1 и x 2 се корените на квадратната равенка x 2 +p x+q=0. Со други зборови, обратната страна на теоремата на Виета е вистинита. Да го формулираме во форма на теорема и да го докажеме.
Теорема.
Ако броевите x 1 и x 2 се такви што x 1 +x 2 =−p и x 1 · x 2 =q, тогаш x 1 и x 2 се корените на намалената квадратна равенка x 2 +p · x+q =0.
Доказ.
Откако ќе се заменат коефициентите p и q во равенката x 2 +p x+q=0 со нивните изрази преку x 1 и x 2 , се трансформира во еквивалентна равенка.
Дозволете ни да го замениме бројот x 1 наместо x во добиената равенка, и ја имаме еднаквоста x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 =0, што за било кој x 1 и x 2 претставува точна бројна еднаквост 0=0, бидејќи x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 = x 1 2 −x 1 2 −x 2 ·x 1 +x 1 ·x 2 =0. Според тоа, x 1 е коренот на равенката x 2 −(x 1 +x 2) x+x 1 x 2 =0, што значи x 1 е коренот на еквивалентната равенка x 2 +p·x+q=0.
Ако во равенката x 2 −(x 1 +x 2) x+x 1 x 2 =0заменете го бројот x 2 наместо x, добиваме еднаквост x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 =0. Ова е вистинска еднаквост, бидејќи x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 = x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0. Според тоа, x 2 е исто така корен на равенката x 2 −(x 1 +x 2) x+x 1 x 2 =0, а со тоа и равенките x 2 +p·x+q=0.
Ова го комплетира доказот на теоремата, обратна страна на теорематаВиета.
Примери за користење на теоремата на Виета
Време е да зборуваме за практичната примена на теоремата на Виета и нејзината обратна теорема. Во овој дел ќе ги анализираме решенијата на неколку од најтипичните примери.
Да почнеме со примена на теоремата конверзна на теоремата на Виета. Удобно е да се користи за да се провери дали дадените два броја се корени на дадена квадратна равенка. Во овој случај се пресметува нивниот збир и разлика, по што се проверува валидноста на односите. Ако и двете од овие релации се задоволени, тогаш врз основа на теоремата која е спротивна на теоремата на Виета, се заклучува дека овие бројки се корените на равенката. Ако барем една од односите не е задоволена, тогаш овие бројки не се корените на квадратната равенка. Овој пристап може да се користи при решавање на квадратни равенки за проверка на пронајдените корени.
Пример.
Кој од паровите броеви 1) x 1 =−5, x 2 =3, или 2) или 3) е пар корени на квадратната равенка 4 x 2 −16 x+9=0?
Решение.
Коефициентите на дадената квадратна равенка 4 x 2 −16 x+9=0 се a=4, b=−16, c=9. Според теоремата на Виета, збирот на корените на квадратната равенка треба да биде еднаков на −b/a, односно 16/4=4, а производот на корените треба да биде еднаков на c/a, односно 9. /4.
Сега да го пресметаме збирот и производот на броевите во секој од трите дадени парови и да ги споредиме со вредностите што штотуку ги добивме.
Во првиот случај имаме x 1 +x 2 =−5+3=−2. Добиената вредност е различна од 4, така што не може да се изврши дополнителна проверка, но користејќи ја теоремата обратна на теоремата на Виета, веднаш може да се заклучи дека првиот пар на броеви не е пар корени на дадената квадратна равенка.
Да преминеме на вториот случај. Овде, односно, првиот услов е исполнет. Го проверуваме вториот услов: добиената вредност е различна од 9/4. Следствено, вториот пар на броеви не е пар корени на квадратната равенка.
Остана уште еден последен случај. Еве и. И двата услови се исполнети, така што овие броеви x 1 и x 2 се корените на дадената квадратна равенка.
Одговор:
Конверзитетот на теоремата на Виета може да се користи во пракса за да се најдат корените на квадратната равенка. Вообичаено, се избираат целобројни корени на дадените квадратни равенки со целобројни коефициенти, бидејќи во други случаи тоа е доста тешко да се направи. Во овој случај, тие го користат фактот дека ако збирот на два броја е еднаков на вториот коефициент на квадратната равенка, земен со знакот минус, а производот од овие броеви е еднаков на слободниот член, тогаш овие броеви се корените на оваа квадратна равенка. Ајде да го разбереме ова со пример.
Да ја земеме квадратната равенка x 2 −5 x+6=0. За броевите x 1 и x 2 да бидат корени на оваа равенка, треба да се задоволат две равенства: x 1 + x 2 =5 и x 1 ·x 2 =6. Останува само да се изберат такви бројки. Во овој случај, ова е прилично едноставно да се направи: таквите броеви се 2 и 3, бидејќи 2+3=5 и 2·3=6. Така, 2 и 3 се корените на оваа квадратна равенка.
Теоремата инверзна на теоремата на Виета е особено погодна за користење за да се најде вториот корен на дадена квадратна равенка кога еден од корените е веќе познат или очигледен. Во овој случај, вториот корен може да се најде од која било од односите.
На пример, да ја земеме квадратната равенка 512 x 2 −509 x −3=0. Овде е лесно да се види дека единството е коренот на равенката, бидејќи збирот на коефициентите на оваа квадратна равенка е еднаков на нула. Значи x 1 = 1. Вториот корен x 2 може да се најде, на пример, од релацијата x 1 ·x 2 =c/a. Имаме 1 x 2 =−3/512, од кои x 2 =−3/512. Вака ги определивме двата корени на квадратната равенка: 1 и −3/512.
Јасно е дека изборот на корени е препорачлив само во повеќето едноставни случаи. Во други случаи, за да најдете корени, можете да користите формули за корените на квадратната равенка преку дискриминатор.
Уште една работа практична применаТеоремата, спротивно на теоремата на Виета, се состои во составување квадратни равенки според дадени корени x 1 и x 2 . За да го направите ова, доволно е да се пресмета збирот на корените, што го дава коефициентот x со спротивен знак на дадената квадратна равенка и производот на корените, кој го дава слободниот член.
Пример.
Напишете квадратна равенка чии корени се −11 и 23.
Решение.
Да означиме x 1 =−11 и x 2 =23. Ги пресметуваме збирот и производот на овие броеви: x 1 +x 2 =12 и x 1 ·x 2 =−253. Според тоа, посочените броеви се корените на намалената квадратна равенка со втор коефициент −12 и слободен член −253. Односно, x 2 −12·x−253=0 е бараната равенка.
Одговор:
x 2 −12·x−253=0.
Теоремата на Виета многу често се користи при решавање на проблеми поврзани со знаците на корените на квадратните равенки. Како е поврзана теоремата на Виета со знаците на корените на намалената квадратна равенка x 2 +p·x+q=0? Еве две релевантни изјави:
- Ако слободниот член q е позитивен број и ако квадратната равенка има реални корени, тогаш или двата се позитивни или и двете негативни.
- Ако слободниот член q е негативен број и ако квадратната равенка има реални корени, тогаш нивните знаци се различни, со други зборови, едниот корен е позитивен, а другиот негативен.
Овие искази произлегуваат од формулата x 1 · x 2 =q, како и од правилата за позитивно множење, негативни броевии броеви со различни знаци. Ајде да погледнеме примери за нивната примена.
Пример.
Р тоа е позитивно. Со помош на формулата за дискриминација наоѓаме D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8, вредноста на изразот r 2 +8 е позитивен за кое било реално r, со тоа D>0 за кое било реално r. Следствено, оригиналната квадратна равенка има два корени за сите реални вредности на параметарот r.
Сега да дознаеме кога корените имаат различни знаци. Ако знаците на корените се различни, тогаш нивниот производ е негативен, а според теоремата на Виета, производот од корените на намалената квадратна равенка е еднаков на слободниот член. Затоа, ние сме заинтересирани за оние вредности на r за кои слободниот член r−1 е негативен. Така, за да ги најдеме вредностите на r што нè интересираат, ни треба одлучи линеарна нееднаквост r−1<0 , откуда находим r<1 .
Одговор:
на р<1 .
Формулите на Виета
Погоре зборувавме за теоремата на Виета за квадратна равенка и ги анализиравме односите што таа ги потврдува. Но, постојат формули кои ги поврзуваат вистинските корени и коефициенти на не само квадратни равенки, туку и кубни равенки, равенки од четврти степен и воопшто, алгебарски равенкистепен n. Тие се нарекуваат Формулите на Виета.
Да ја напишеме формулата Виета за алгебарска равенка со степен n на формата и ќе претпоставиме дека има n вистински корени x 1, x 2, ..., x n (меѓу нив може да има и коинцидираат): 
Може да се добијат формули на Виета теорема за разложување на полином на линеарни фактори, како и дефинирање на еднакви полиноми преку еднаквост на сите нивни соодветни коефициенти. Значи полиномот и неговото проширување во линеарни фактори на формата се еднакви. Отворајќи ги заградите во последниот производ и изедначувајќи ги соодветните коефициенти, ги добиваме формулите на Виета.
Конкретно, за n=2 ги имаме веќе познатите Vieta формули за квадратна равенка.
За кубна равенка, формулите на Виета ја имаат формата 
Останува само да се забележи дека на левата страна од формулите на Виета се наоѓаат т.н. симетрични полиноми.
Референци.
- Алгебра:учебник за 8 одделение. општо образование институции / [Ју. Н. Макаричев, Н. Г. Миндјук, К. И. Нешков, С. Б. Суворова]; уредено од С.А. Телјаковски. - 16-ти изд. - М.: Образование, 2008. - 271 стр. : болен. - ISBN 978-5-09-019243-9.
- Мордкович А.Г.Алгебра. 8-мо одделение. За 2 часа, дел 1. Учебник за студенти од општообразовни институции / А. Г. Мордкович. - 11-то издание, избришано. - М.: Мнемозина, 2009. - 215 стр.: илуст. ISBN 978-5-346-01155-2.
- Алгебраи почетокот на математичката анализа. 10-то одделение: учебник. за општо образование институции: основни и профил. нивоа / [Ју. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; уредено од А.Б. Жижченко. - 3-то издание. - М.: Образование, 2010.- 368 стр. : болен. - ISBN 978-5-09-022771-1.