I = ∑r јас 2 dF i =∫r 2 dF (1.1)
Во принцип, и дефиницијата и формулата што го опишуваат не се комплицирани и нивното запомнување е многу полесно отколку разбирањето на суштината. Но, сепак, да се обидеме да откриеме кој е моментот на инерција и од каде доаѓа.
Концептот на моментот на инерција дошол до силата на материјалите и структурната механика од друга гранка на физиката која ја проучува кинематиката на движењето, особено ротационото движење. Но, сепак да почнеме од далеку.
Не знам со сигурност дали јаболко му паднало на главата на Исак Њутн, дали паднало во близина или воопшто не паднало; теоријата на веројатност ги дозволува сите овие опции (покрај тоа, има премногу во ова јаболко од библиската легенда за дрвото на знаењето), но сигурен сум дека Њутн бил внимателен човек, способен да извлече заклучоци од своите набљудувања. Така, набљудувањето и имагинацијата му дозволија на Њутн да го формулира основниот закон на динамиката (вториот Њутнов закон), според кој масата на телото м, помножено со забрзување а, е еднаква на дејствувачката сила П(всушност, ознаката F е почеста за сила, но бидејќи понатаму ќе се занимаваме со површина, која исто така често се означува како F, јас ја користам ознаката Q за надворешната сила, сметана во теоретската механика како концентрирано оптоварување, всушност не се менува):
Q = ма (1.2)
За мене, големината на Њутн лежи во неговата едноставност и јасност. оваа дефиниција. Исто така, ако се земе предвид дека кога подеднакво забрзано движењезабрзување Аеднаков на односот на зголемување на брзината ΔVдо одреден временски период Δt, при што брзината се промени:
a = Δv/Δt = (v - v о)/t (1.3.1)
на V o = 0 a = v/t (1.3.2)
тогаш можете да ги одредите основните параметри на движење, како растојание, брзина, време, па дури и моментум Р, карактеризирајќи ја количината на движење:
p = mv (1.4)
На пример, јаболкото кое паѓа од различни висини само под влијание на гравитацијата ќе падне на земја различно време, имаат различни брзини во моментот на слетување и, соодветно, различни импулси. Со други зборови, на јаболкото кое паѓа од поголема височина ќе му треба подолго време да лета и ќе пукне посилно по челото на несреќниот набљудувач. И Њутн сето ова го сведе на едноставна и разбирлива формула.
Њутн го формулирал и законот за инерција (првиот закон на Њутн): ако забрзување a = 0, потоа во инерцијален системреферентна точка, невозможно е да се одреди дали набљудуваното тело, на кое не дејствуваат надворешни сили, е во мирување или се движи во права линија со постојана брзина. Ова својство на материјалните тела да ја одржуваат својата брзина, дури и нула, се нарекува инерција. Мерката за инерција е инерцијалната маса на телото. Понекогаш инерцијалната маса се нарекува инертна, но тоа не ја менува суштината на материјата. Се верува дека инерцијалната маса е еднаква на гравитационата маса и затоа често не се прецизира за која маса се мисли, туку едноставно се споменува масата на телото.
Не помалку важен и значаен е третиот закон на Њутн, според кој акционата сила е еднаква на силата на реакција ако силите се насочени во една права линија, но во спротивни насоки. И покрај неговата очигледна едноставност, овој заклучок на Њутн е брилијантен и важноста на овој закон е тешко да се прецени. Една од примените на овој закон е разгледана подолу.
Меѓутоа, овие одредби важат само за тела кои се движат преводно, т.е. по прав пат и во исто време сè материјални точкитаквите тела се движат со иста брзина или исто забрзување. За криволиниско движење и особено за ротационо движење, на пример, кога телото ротира околу својата оска на симетрија, материјалните точки на такво тело се движат во просторот со иста аголна брзина w, но во исто време и линеарната брзина vразлични точки ќе имаат различни вредности и оваа линеарна брзина е директно пропорционална на растојанието род оската на ротација до оваа точка:
v=wr (1.5)
во овој случај, аголната брзина е еднаква на односот на зголемувањето на аголот на ротација Δφ до одреден временски период Δt, за кој аголот на ротација е променет:
w = Δφ/Δt = (φ - φ о)/t (1.6.1)
на φ o = 0 w = φ/t (1.7.2)
соодветно нормално забрзување и nза време на ротационото движење е еднакво на:
a n = v 2 /r = w 2 r (1.8)
И излегува дека за ротационо движење не можеме директно да ја користиме формулата (1.2), бидејќи при ротационото движење вредноста на телесната маса сама не е доволна; ние исто така треба да ја знаеме распределбата на оваа маса во телото. Излегува дека колку материјалните точки на телото се поблиску до оската на ротација, толку помалку сила мора да се примени за да се ротира телото и обратно, колку материјалните точки на телото се подалеку од оската на ротација, толку поголема сила мора да се примени за да се присили телото да ротира (во овој случај зборуваме за примена на сила во истата точка). Покрај тоа, при ротирање на телото, попогодно е да се земе предвид дека не ефективна сила, и вртежниот момент, бидејќи при ротационо движење има и точката на примена на силата големо значење.
Неверојатните својства на вртежниот момент ни се познати уште од времето на Архимед, а ако го примениме концептот на вртежен момент на ротационото движење, тогаш значењето на вртежниот момент Мќе биде поголемо колку е поголемо растојанието род оската на ротација до точката на примена на сила Ф(во структурна механика надворешна силачесто се нарекува како Рили П):
M = Qr (1.9)
Од оваа исто така не многу комплицирана формула произлегува дека ако се примени сила долж оската на ротација, тогаш нема да има ротација, бидејќи r = 0, а ако силата се примени на максималното растојание од оската на ротација, тогаш вредноста на моментот ќе биде максимална. И ако ја замениме во формулата (1.9) вредноста на силата од формулата (1.2) и вредноста на нормалното забрзување и формулата (1.8), ја добиваме следната равенка:
M = mw 2 r r = mw 2 r 2 (1.10)
Во конкретниот случај кога телото е материјална точка со димензии многу помали од растојанието од оваа точка до оската на ротација, равенката (1.10) е применлива во чиста форма. Меѓутоа, за тело што ротира околу една од неговите оски на симетрија, растојанието од секоја материјална точка што го сочинува ова тело е секогаш помало од една од геометриските димензии на телото и затоа распределбата на масата на телото е од голема важност. во овој случај потребно е да се земат предвид овие растојанија посебно за секоја точка:
M = ∑r i 2 w 2 m јас (1.11.1)
М с = w 2 ∫r 2 dm
И тогаш излегува дека, според третиот закон на Њутн, како одговор на дејството на вртежниот момент, ќе се појави таканаречениот момент на инерција Јас. Во овој случај, вредностите на вртежниот момент и моментот на инерција ќе бидат еднакви, а самите моменти ќе бидат насочени во спротивни насоки. При константна аголна брзина на ротација, на пример w = 1, главните количини што го карактеризираат вртежниот момент или моментот на инерција ќе бидат масата на материјалните точки што го сочинуваат телото и растојанијата од овие точки до оската на ротација. Како резултат на тоа, формулата за моментот на инерција ќе ја има следната форма:
[- M] = I = ∑r i 2 m јас (1.12.1)
I c = ∫r 2 dm(1.11.2) - кога телото ротира околу оската на симетрија
Каде Јас- општо прифатената ознака за моментот на инерција, Иц- означување на аксијалниот момент на инерција на телото, kg/m 2. За хомогено тело со иста густина ρ низ целото тело ВФормулата за аксијалниот момент на инерција на телото може да се запише на следниов начин:
I c = ∫ρr 2 dV (1.13)
Така, моментот на инерција е мерка за инертноста на телото за време на ротационото движење, исто како што масата е мерка за инерцијата на телото за време на транслаторното праволиниско движење.
Кругот стана полн круг. И тука може да се појави прашањето, каква врска имаат сите овие закони на динамика и кинематика со пресметката на статичните градежни конструкции? Излегува дека ниту едното не е најдиректно и најнепосредно. Прво, затоа што сите овие формули беа изведени од физичарите и математичарите во тие далечни времиња кога такви дисциплини како „Теоретска механика“ или „Теорија на јачината на материјалите“ едноставно не постоеја. И второ, затоа што целата пресметка на градежните конструкции се заснова на посочените закони и формулации и изјавата што се уште не е побиена од никого за еднаквоста на гравитационите и инерцијалните маси. Но, во теоријата на јачината на материјалите сè е сепак поедноставно, без разлика колку парадоксално звучи.
И тоа е поедноставно затоа што при решавање на одредени проблеми не може да се земе предвид целото тело, туку само неговиот пресек и, доколку е потребно, неколку пресеци. Но, во овие делови дејствуваат истите физички сили, иако од малку поинаква природа. Така, ако земеме предвид одредено тело чија должина е константна, а самото тело е хомогено, тогаш ако не ги земеме предвид константните параметри - должина и густина ( l = const, ρ = const) - ќе добиеме модел пресек. За таков пресек, од математичка гледна точка, ќе важи следнава равенка:
I р = ∫r 2 dF (2.1) → (1.1)
Каде Ип- поларен момент на инерција на пресекот, m 4. Како резултат на тоа, ја добивме формулата со која започнавме (но дали стана појасно кој е моментот на инерција на делот, не знам).
Бидејќи во теоријата на јачината на материјалите често се разгледуваат правоаголни пресеци, а правоаголниот координатен систем е поудобен, при решавање на проблеми, обично се земаат предвид два аксијални моменти на инерција на пресекот:
I z = ∫y 2 dF (2.2.1)
I y = ∫z 2 dF (2.2.2)
Слика 1. Координатни вредности при одредување на аксијални моменти на инерција.
Тука може да се појави прашањето зошто се користат секири zИ на, а не оние попознатите XИ на? Се случува определувањето на силите во пресек и изборот на дел кој може да издржи работни напрегања еднакви на применетите сили се две различни задачи. Првата задача - определување на силите - се решава со структурна механика, втората задача - избор на пресеци - се решава со теоријата на јачината на материјалите. Во исто време, во структурната механика се зема предвид при решавање едноставни задачидоста често прачка (за праволиниски структури) со одредена должина л, а висината и ширината на пресекот не се земени во предвид, додека се смета дека ос Xпрецизно минува низ центрите на гравитација на сите пресеци и на тој начин, при конструирање дијаграми (понекогаш прилично сложени), должината лпрецизно се депонира по оската X, и по должината на оската наВредностите на заплетот се нацртани. Во исто време, теоријата на цврстина на материјалите го зема предвид токму пресекот, за кој ширината и висината се важни, а должината не се зема предвид. Се разбира, при решавање на проблеми во теоријата на јачината на материјалите, кои исто така понекогаш се прилично сложени, се користат истите познати оски XИ на. Оваа состојба ми се чини дека не е сосема точна, бидејќи и покрај разликата, ова се сè уште поврзани задачи и затоа би било посоодветно да се користат заеднички оски за структурата што се пресметува.
Вредноста на поларниот момент на инерција во правоаголен координатен систем ќе биде:
I р = ∫r 2 dF =∫y 2 dF + ∫z 2 dF (2.3)
Бидејќи во правоаголен координатен систем радиусот е хипотенузата правоаголен триаголник, и како што знаете, квадратот на хипотенузата е еднаков на збирот на квадратите на катетите. И тука е и концептот на центрифугалниот момент на инерција на пресекот:
I xz = ∫xzdF(2.4)
Помеѓу оските на правоаголниот координатен систем што минуваат низ тежиштето на пресекот, постојат две меѓусебно нормални оски, во однос на кои аксијалните моменти на инерција ги добиваат максималните и минималните вредности, додека центрифугалниот момент на инерција на дел I zy = 0. Таквите оски се нарекуваат главни централни оски на напречниот пресек, а моментите на инерција околу таквите оски се нарекуваат главни централни моменти на инерција
Кога зборуваме за моменти на инерција во теоријата на јачината на материјалите, најчесто мислиме на главните централни моменти на инерција на пресекот. За квадратни, правоаголни, кружни делови, главните оски ќе се совпаѓаат со оските на симетрија. Моментите на инерција на попречниот пресек се нарекуваат и геометриски моменти на инерција или плоштини моменти на инерција, но суштината останува иста.
Во принцип, нема голема потреба да се одредат вредностите на главните централни моменти на инерција за пресеците на најчестите геометриски форми - квадрат, правоаголник, круг, цевка, триаголник и некои други. Ваквите моменти на инерција одамна се дефинирани и нашироко познати. И кога се пресметуваат аксијални моменти на инерција за делови од комплекс геометриска формавалидна е теоремата Хајгенс-Штајнер:
I = I c + r 2 F (2.5)
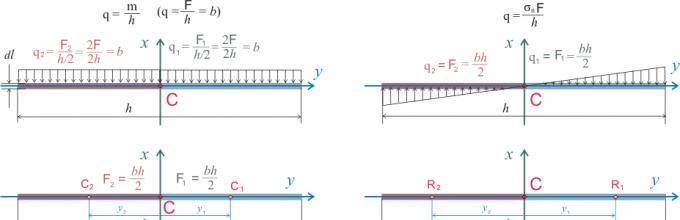
Така, ако областите и центрите на гравитација на едноставни геометриски форми, составувајќи комплексен пресек, а потоа да се одреди вредноста на аксијалниот момент на инерција на целиот дел не е тешко. А за да се одреди тежиштето на комплексен пресек, се користат статичките моменти на пресекот. Статичните моменти се дискутирани подетално во друга статија, само ќе додадам овде. Физичкото значење на статичкиот момент е следново: статичкиот момент на телото е збир на моменти за материјалните точки што го сочинуваат телото, во однос на одредена точка (поларен статички момент) или во однос на оската (аксијален статичен момент ), а бидејќи моментот е производ на сила и крак (1.9) , тогаш соодветно се одредува статичкиот момент на телото:
S = ∑M = ∑r јасм јас= ∫rdm (2.6)
и тогаш поларниот статички момент на пресекот ќе биде:
S р = ∫rdF (2.7)
Како што можете да видите, дефиницијата за статички момент е слична на дефиницијата за момент на инерција. Но, постои фундаментална разлика. Статичкиот момент се нарекува статичен затоа што за тело на кое дејствува гравитационата сила, статичкиот момент е еднаков на нула во однос на центарот на гравитација. Со други зборови, ваквото тело е во состојба на рамнотежа ако потпорот е нанесен на центарот на гравитација на телото. И според првиот Њутнов закон, таквото тело или мирува или се движи со постојана брзина, т.е. забрзување = 0. А од чисто математички аспект статичкиот вртежен момент може да биде еднаков на нула од едноставна причина што при определувањето на статичкиот вртежен момент потребно е да се земе предвид насоката на дејство на вртежниот момент. На пример, во однос на координатните оски што минуваат низ центарот на гравитација на правоаголникот, областите на горниот и долниот дел од правоаголникот ќе бидат позитивни бидејќи ја симболизираат силата на гравитацијата што дејствува во една насока. Во овој случај, растојанието од оската до центарот на гравитација може да се смета за позитивно (условно: моментот од гравитационата сила на горниот дел од правоаголникот се обидува да го ротира делот во насока на стрелките на часовникот), а до центарот на гравитација на долниот дел - како негативен (условно: моментот од гравитационата сила на долниот дел од правоаголникот се обидува да го ротира делот спротивно од стрелките на часовникот). И бидејќи таквите области се нумерички еднакви и еднакви на растојанијата од центрите на гравитација на горниот дел на правоаголникот и долниот дел од правоаголникот, тогаш збирот на актерските моменти ќе биде посакуваната 0.
S z = ∫ydF = 0 (2.8)
Оваа голема нула, исто така, овозможува да се одредат реакциите за поддршка на градежните конструкции. Ако земеме во предвид градежна конструкција на која, на пример, се применува концентрирано оптоварување Q во одредена точка, тогаш таквата градежна конструкција може да се смета како тело со центар на гравитација во точката на примена на силата, а реакциите на поддршка во овој случај се сметаат како сили кои се применуваат на точките на поддршка. Така, знаејќи ја вредноста на концентрираното оптоварување Q и растојанието од точката на нанесување на товарот до носачите на градежната конструкција, можно е да се одредат реакциите на потпора. На пример, за едноставно поддржан сноп на две потпори, вредноста на реакциите за поддршка ќе биде пропорционална на растојанието до точката на примена на силата, а збирот на реакциите за поддршка ќе биде еднаков на применетиот товар. Но, по правило, при одредување на реакциите за поддршка, тие се одвиваат уште поедноставно: една од потпорите се зема како центар на гравитација, а потоа збирот на моментите од применетиот товар и од преостанатите реакции на поддршка е сè уште еднаков на нула. Во овој случај, моментот од потпорната реакција во однос на кој е составена равенката на моментот е еднаков на нула, бидејќи раката на силата = 0, што значи дека во збирот на моментите остануваат само две сили: применетото оптоварување и непознатата потпорна реакција (за статички детерминирани структури).
Така, фундаменталната разлика помеѓу статичкиот момент и моментот на инерција е во тоа што статичкиот момент го карактеризира делот што силата на гравитација се обидува да го скрши на половина во однос на центарот на гравитација или оската на симетрија, и моментот на инерцијата го карактеризира телото, чиишто материјални точки се движат (или се обидуваат да се движат во една насока). Можеби следните прилично конвенционални шеми за пресметување за правоаголен дел ќе помогнат појасно да се замисли оваа разлика:

Слика 2. Јасна разлика помеѓу статичкиот момент и моментот на инерција.
Сега да се вратиме уште еднаш на кинематиката на движењето. Ако извлечеме аналогии помеѓу напрегањата кои се јавуваат во пресеците на градежните конструкции и различните видови на движење, тогаш кај централно растегнатите и централно компресираните елементи се јавуваат напрегања кои се униформни на целата површина на пресекот. Овие напрегања може да се споредат со дејството на некоја сила врз телото, при што телото ќе се движи праволиниско и прогресивно. А најинтересно е што пресеците на централно истегнатите или централно компресираните елементи всушност се движат, бидејќи дејствувачките напрегања предизвикуваат деформации. И големината на таквите деформации може да се одреди за кој било пресек на структурата. За да го направите ова, доволно е да се знае вредноста на ефективни напрегања, должината на елементот, површината на напречниот пресек и модулот на еластичност на материјалот од кој е направена конструкцијата.
За елементите што се виткаат, пресеците исто така не остануваат на своето место, туку се движат, а движењето на пресеците на свитливите елементи е слично на ротацијата на одредено тело околу одредена оска. Како што веројатно веќе погодивте, моментот на инерција ви овозможува да го одредите аголот на наклон на пресекот и поместувањето Δ л за екстремните точки на делот. Овие екстремни точки за правоаголен пресек се наоѓаат на растојание еднакво на половина од висината на пресекот (зошто е доволно детално опишано во статијата „Основи на јачината на јачината. Определување на отклон“). И ова, пак, ви овозможува да го одредите отклонувањето на структурата.
И моментот на инерција ви овозможува да го одредите моментот на отпорност на делот. За да го направите ова, моментот на инерција мора едноставно да се подели со растојанието од центарот на гравитација на пресекот до најоддалечената точка на пресекот, за правоаголен пресек со h/2. И бидејќи деловите што се проучуваат не се секогаш симетрични, вредноста на моментот на отпор може да биде различна за различни делови од делот.
И се започна со банално јаболко... иако не, се започна со збор.
§ 4.5. ПРЕСМЕТКА НА МОМЕНТИ НА ИНЕРЦИЈА НА ПРЕСЕКИ НА ЕДНОСТАВНА ФОРМА
Како што е наведено во § 1.5, геометриските карактеристики на сложените пресеци се одредуваат со нивно делење на голем број едноставни фигури, чии геометриски карактеристики може да се пресметаат со соодветни формули или да се утврдат со помош на специјални табели. Овие формули се добиени како резултат на директно интегрирање на изразите (8.5)-(10.5). Методите за нивно добивање се дискутирани подолу користејќи примери на правоаголник, триаголник и круг.
Правоаголен пресек
Дозволете ни да го одредиме аксијалниот момент на инерција на правоаголник со висина h и ширина b во однос на оската што минува низ неговата основа (сл. 11.5, а). Да избереме од правоаголникот со прави паралелни на оската елементарна лента со висина и ширина b.
Областа на оваа лента, растојанието од лентата до оската е еднакво на нив. Ајде да ги замениме овие величини во изразот за моментот на инерција (8.5):
На сличен начин, за моментот на инерција околу оската, може да се добие изразот
За да го одредиме центрифугалниот момент на инерција, избираме од правоаголникот со линии паралелни на оските (Сл.
11.5, б), елементарна област со големина. Прво да го одредиме центрифугалниот момент на инерција не на целиот правоаголник, туку само на вертикална лента со висина h и ширина која се наоѓа на растојание од оската
Производот е поставен надвор од интегралниот знак, бидејќи за сите области кои припаѓаат на вертикалната лента што се разгледува, тој е константен.
Дозволете ни да го интегрираме изразот во опсегот од до
Сега да ги одредиме аксијалните моменти на инерција на правоаголникот во однос на y и оските што минуваат низ центарот на гравитација паралелно со страните на правоаголникот (сл. 12.5). За овој случај, границите на интеграцијата ќе бидат од до
Центрифугалниот момент на инерција на правоаголникот во однос на оските (сл. 12.5) е еднаков на нула, бидејќи овие оски се совпаѓаат со неговите оски на симетрија.
Триаголен пресек
Дозволете ни да ги одредиме аксијалните моменти на инерција на триаголникот во однос на трите паралелни оски што минуваат низ неговата основа (сл. 13.5, а), тежиштето (сл. 13.5, б) и темето (сл. 13.5, д).
За случајот кога оската минува низ основата на триаголникот (сл. 13.5, а),
За случај кога оската минува низ тежиштето на триаголникот паралелно со неговата основа (сл. 13.5, б),
Во случај кога оската минува низ темето на триаголникот паралелно со неговата основа (сл. 13.5, в),
Моментот на инерција е значително поголем (три пати) од моментот на инерција бидејќи главниот дел од областа на триаголникот е пооддалечен од оската отколку од оската
Добиени се изрази (17.5) - (19.5) за рамнокрак триаголник. Сепак, тие важат и за нерамнокраки триаголници. Споредувајќи ги, на пример, триаголниците прикажани на сл. 13.5, a и 13.5, d, од кои првиот е рамнокрак, а вториот не е рамнокрак, утврдуваме дека димензиите на плоштината и границите во кои y варира (од 0 до) се исти за двата триаголници. Следствено, моментите на инерција за нив се исто така исти. Слично на тоа, може да се покаже дека аксијалните моменти на инерција на сите делови прикажани на сл. 14,5 се исти. Општо земено, поместувањето на делови од делот паралелно на одредена оска не влијае на вредноста на аксијалниот момент на инерција во однос на оваа оска.
Очигледно е дека збирот на аксијалните моменти на инерција на триаголникот во однос на оските прикажани на сл. 13.5, a и 13.5, b, треба да бидат еднакви на аксијалниот момент на инерција на правоаголникот во однос на оската прикажана на сл. 11.5, а. Ова произлегува од фактот дека правоаголникот може да се смета како два триаголници, од кои едниот оската минува низ основата, а за другиот низ темето паралелно со неговата основа (сл. 15.5).
Навистина, според формулите (17.5) и (19.5)
што се совпаѓа со изразот на правоаголникот според формулата (12.5).
Пресек во форма на круг
Дозволете ни да го одредиме аксијалниот момент на инерција на кругот во однос на која било оска што минува низ неговиот центар на гравитација. Од Сл. 16,5, но треба
Очигледно е дека во однос на која било оска што минува низ центарот на кругот, аксијалниот момент на инерција ќе биде еднаков и затоа,
Користејќи ја формулата (11.5) го наоѓаме поларниот момент на инерција на кругот во однос на неговиот центар:
Формулата за аксијалниот момент на инерција на кругот може да се добие на поедноставен начин ако прво ја изведете формулата за неговиот поларен момент на инерција во однос на центарот (точка O). За да го направите ова, избираме елементарен прстен од кругот со дебелина на радиус и површина (слика 16.5, б).
Поларниот момент на инерција на елементарен прстен во однос на центарот на кругот, бидејќи сите елементарни области од кои се состои овој прстен се наоѓаат на исто растојание од центарот на кругот. Оттука,
Овој резултат се совпаѓа со оној добиен погоре.
Моментите на инерција (поларна и аксијална) на пресек во облик на кружен прстен со надворешен и внатрешен дијаметар d (сл. 17.5) може да се одредат како разлика помеѓу соодветните моменти на инерција на надворешните и внатрешните кругови.
Поларен момент на инерција на прстенот врз основа на формулата (21,5)
или, ако назначиме
Слично на тоа, за аксијалните моменти на инерција на прстенот
Момент на инерција и момент на отпор
При определување на пресекот на градежните конструкции, често е потребно да се знае моментот на инерција и моментот на отпор за пресекот на конструкцијата што се разгледува. Кој е моментот на отпор и како тој е поврзан со моментот на инерција е опишан одделно. Покрај тоа, за компресибилни структури исто така треба да ја знаете вредноста на радиусот на вртење. Моментот на отпор и моментот на инерција, а понекогаш и радиусот на вртење за повеќето пресеци со едноставна геометриска форма може да се одредат со помош на добро познати формули:
Табела 1. Пресечни форми, области на попречни пресек, моменти на инерција и моменти на отпор за структури со прилично едноставни геометриски форми.
Обично, овие формули се доволни за повеќето пресметки, но има секакви случаи и пресекот на структурата може да нема толку едноставна геометриска форма или положба на оските за кои е потребен моментот на инерција или моментот на отпор. што треба да се одреди можеби не е исто, тогаш можете да ги користите следните формули:
Табела 2. Пресечни форми, области на попречни пресек, моменти на инерција и моменти на отпор за структури од посложени геометриски форми

Како што може да се види од Табела 2, пресметувањето на моментот на инерција и моментот на отпор за нееднакви агли е доста тешко, но нема потреба за тоа. Постојат асортимани за нееднакви и еднакви валани агли на прирабница, како и за канали, I-зраци и профилни цевки. ВО асортимани За секој профил се дадени вредностите на моментот на инерција и моментот на отпор.
Табела 3. Промени во моментите на инерција и моменти на отпор во зависност од положбата на оските.

Формулите од Табела 3 може да бидат потребни за пресметување на навалените елементи на покривот.
Би било убаво да се објасни со јасен пример за особено надарените луѓе, како мене, што е моментот на инерција и со што се користи. На специјализирани сајтови, сè е некако многу збунувачки, но Док има јасен талент за пренесување информации, можеби не најкомплексни, но многу компетентни и разбирливи
Во принцип, што е момент на инерција и од каде доаѓа е објаснето доволно детално во написот „Основи на јачината, пресметковни формули“, овде само ќе повторам: „W е моментот на отпор на пресекот на зракот, со други зборови, површината на компримираниот или затегнувачкиот дел од делот на зракот, помножен со раб на дејство на резултантната сила“. Моментот на отпор мора да биде познат за пресметки на силата на конструкцијата, т.е. според крајните напрегања. Моментот на инерција мора да биде познат за да се одредат аглите на ротација на пресекот и отклонот (поместувањето) на центарот на гравитација на пресекот, бидејќи максималните деформации се случуваат во најгорните и најниските слоеви на структурата на свиткување, моментот на инерција може да се определи со множење на моментот на отпор со растојанието од пресеците на центарот на гравитација до горниот или долниот слој, затоа за правоаголните пресеци I=Wh/2. При определување на моментот на инерција на пресеци од сложени геометриски форми, прво сложената фигура се дели на едноставни, потоа се одредуваат плоштините на попречните пресекови на овие фигури и моментите на инерција на наједноставните фигури, а потоа плоштините на наједноставните бројките се множат со квадратот на растојанието од општиот центар на гравитација на делот до центарот на гравитација на наједноставната фигура. Моментот на инерција на наједноставната фигура како дел од сложен пресек е еднаков на моментот на инерција на фигурата + квадратот на растојанието помножено со плоштината. Потоа се сумираат добиените моменти на инерција и се добива моментот на инерција на сложениот пресек. Но, ова се најпоедноставените формулации (иако, се согласувам, сепак изгледа прилично незгодно).
Момент на инерција и момент на отпор - д-р Лом
При определување на пресекот на градежните конструкции често е потребно да се знае моментот на инерција и моментот на отпор за пресекот на конструкцијата. Моментот на отпор и моментот на енергија за огромното мнозинство на пресеци со едноставна геометриска форма може да се одредат со користење на одамна познати формули
Поглавје 5. МОМЕНТИ НА ИНЕРЦИЈА НА РАМНИ ПРЕСЕКИ
Секој рамен пресек се карактеризира со голем број геометриски карактеристики: површина, координати на центарот на гравитација, статички момент, момент на инерција итн.
Статични моменти за оските XИ yсе еднакви:
Статичните моменти обично се изразуваат во кубни сантиметри или метри и можат да имаат и позитивни и негативни вредности. Се нарекува оската околу која статичкиот момент е нула централно.Точката на пресек на централните оски се нарекува центар на гравитација на делот. Формули за одредување на координатите на центарот на гравитација x вИ y cкомплексен пресек, поделен на едноставни компоненти за кои се познати областите А ии положбата на центарот на гравитација xciИ y ci, имаат форма
Големината на моментот на инерција ја карактеризира отпорноста на шипката на деформација (торзија, свиткување) во зависност од големината и обликот на пресекот. Постојат моменти на инерција:
– аксијален, определен со интеграли на формата
Аксијалните и поларните моменти на инерција се секогаш позитивни и не
оди на нула. Поларен момент на инерција Ипеднаков на збирот на аксијалните моменти на инерција јас xИ Јасво однос на кој било пар меѓусебно нормални оски XИ на:
Центрифугалниот момент на инерција може да биде позитивен, негативен или нула. Димензијата на моментите на инерција е cm 4 или m 4. Формулите за одредување на моментите на инерција на едноставни пресеци во однос на централните оски се дадени во референтни книги. При пресметување на моментите на инерција на сложените пресеци, често се користат формули за премин од централните оски на едноставни пресеци до други оски паралелни на централните.
каде се моментите на инерција на едноставни пресеци во однос на централните оски;
m, n– растојанија меѓу оските (сл. 18).

Ориз. 18. Да се одредат моментите на инерција околу оските,
Важни се главните централни оски на делницата. Главните централни оски се две меѓусебно нормални оски кои минуваат низ центарот на гравитација на пресекот, во однос на кои центрифугалниот момент на инерција е нула, а аксијалните моменти на инерција имаат екстремни вредности. Наведени се главните моменти на инерција јас ти(макс) и јас v(мин) и се одредуваат со формулата
Позицијата на главните оски се одредува со аголот α, кој се наоѓа од формулата
Аголот α е отпуштен од оската со голем неглавен момент на инерција; позитивна вредност- спротивно од стрелките на часовникот.
Ако делот има оска на симетрија, тогаш оваа оска е главната. Другата главна оска е нормална на оската на симетрија. Во пракса, често се користат делови составени од неколку валани профили (I-зрак, канал, агол). Геометриските карактеристики на овие профили се дадени во табелите со асортиман. За нееднакви и рамностран агли, центрифугалниот момент на инерција во однос на централните оски паралелни на прирабниците се одредува со формулата
Обрнете внимание на означувањето на главните централни оски во табелата со асортиман за аглите. Потпишете Јас xyза агол зависи од неговата положба во делот. Слика 19 ги прикажува можните позиции на аголот во делот и ги прикажува знаците за Јас xy.
Ориз. 19. Можни позиции на аголот во делот
Дефинирај Иу, Иви положбата на главните централни оски на делницата
Комплексен дел се состои од два валани профили. Извадок од табелите за асортиман (Додаток 5) е прикажан на сл. 21.
Како помошни ќе ги земеме оските што минуваат по надворешната
страни на каналот (оска x Б, y Б, види сл. 20).Координати на тежиштето на пресекот:
(пресметајте сами).

Ориз. 20. Положба на главните централни оски на инерција
УИ Вкомплексен дел
Може да се изберат, на пример, централните оски на каналот како помошни. Тогаш износот на пресметки ќе биде малку намален.
Аксијални моменти на инерција:
Ве молиме имајте предвид дека нееднаков агол во делот се наоѓа
поинаку од прикажаното во табелата со асортиман. Пресметајте ја вредноста сами.

бр. 24 180 x 110 x 12
Ориз. 21. Вредности на геометриските карактеристики на валани профили:
А– канал бр.24; б– нееднаков агол 180 x 110 x 12
Центрифугални моменти на инерција:
– за канал (има оски на симетрија);
- за аголот,
знак минус - поради положбата на аголот во делот;
– за целиот дел:
Следете ја целта на знаците nИ м. Од централните оски на каналот преминуваме кон заедничките централни оски на делот, затоа + m 2
Главните моменти на инерција на делот:
Позиција на главните централни оски на делницата:
; α = 55 o 48 ';
Проверка на исправноста на пресметката на количините јас ти, јас vа α се произведува со формулата
Аголот α за оваа формула се мери од оската u.
Разгледаниот дел има најголема отпорност на свиткување во однос на оската uа најмалиот – во однос на оската v.
Поглавје 5. МОМЕНТИ НА ИНЕРЦИЈА НА РАМНИ ПРЕСЕКИ Секој рамен пресек се карактеризира со голем број геометриски карактеристики: површина, координати на центарот на гравитација, статички момент, момент на инерција и
Се разликуваат следните типови на моменти на инерција на пресеците: аксијален; центрифугални; поларна; централни и главни моменти на инерција.
Центрифугални моменти на инерцијарелативни пресеци наИ zсе нарекува интеграл од формата Збирот на аксијалните моменти на инерција на пресек во однос на две координатни оски е еднаков на поларниот момент на инерција во однос на потеклото:Димензијата на наведените типови на моменти на инерција на пресекот (должина 4), т.е. m 4 или cm 4.
Аксијалните и поларните моменти на инерција на пресекот се позитивни величини; центрифугалниот момент на инерција може да биде позитивен, негативен и еднаков на нула (за некои оски кои се оска на симетрија).
Постојат зависности за моменти на инерција при паралелно преведување и ротирање на координатните оски.
 Слика 5.4 – Паралелно преведување и ротација на координатните оски за произволен пресек на зрак
Слика 5.4 – Паралелно преведување и ротација на координатните оски за произволен пресек на зрак
Ако се познати моментите на инерција на пресекот Iz, Iу, Izуво однос на оските zИ на, потоа моментите на инерција околу ротираните оски z 1И во 1, под агол α во однос на оригиналните оски (сл. 5.4, б) се одредува со формулите:

Со концептот главните моменти на инерцијаја поврзуваат положбата на главните оски на инерција. Главните оски на инерцијасе нарекуваат две меѓусебно нормални оски, во однос на кои центрифугалниот момент на инерција е еднаков на нула, а аксијалните моменти добиваат екстремни вредности (максимални и минимални).
Ако главните оски минуваат низ центарот на гравитација на фигурата, тогаш тие се нарекуваат главните централни оски на инерција.
Позицијата на главните оски на инерција се наоѓа од следните зависности:При пресметувањето на јачината на структурните елементи, тие го користат концептот на таква геометриска карактеристика како модул на пресек.
Да го разгледаме, на пример, пресекот на зракот (сл. 5.5).

Слика 5.5 – Пример за пресек на греда
Растојание на најоддалечените т. Аод центарот на гравитација на делот т.е. С зазначајни ч 1,и растојанието т. ВО- преку ч 2.
| (5.16) |
Практичен интерес за пресметките на силата е најмалиот момент на отпор на делот Wmin, што одговара на најоддалечените т. Аод центарот на гравитација на делот h 1 = y макс.
Димензија на елементите на отпорот (должина 3), т.е. m 3, cm 3.
Табела 5.1 - Вредности на моменти на инерција и моменти на отпор на наједноставните делови во однос на централните оски
| Видови имиња на секции | Моменти на инерција | Моменти на отпор | ||
| Правоаголник |  | |||
| Заокружете |  | |
продолжение на табела 5.1
Да воведеме декартов правоаголен координатен систем O xy. Да разгледаме произволен пресек (затворена област) со површина А во координатната рамнина (сл. 1).
Статични моменти

Точка C со координати (x C , y C)

повикани центар на гравитација на делот.
Ако координатните оски минуваат низ центарот на гравитација на пресекот, тогаш статичките моменти на пресекот се еднакви на нула:
Аксијални моменти на инерцијапресеците во однос на оските x и y се нарекуваат интеграли од формата:

Поларен момент на инерцијаделот во однос на потеклото на координатите се нарекува интеграл на формата:
![]()
Центрифугален момент на инерцијаделот се нарекува интеграл на формата:

Главните оски на инерција на делотсе нарекуваат две меѓусебно нормални оски, во однос на кои I xy = 0. Ако една од меѓусебно нормалните оски е оската на симетрија на пресекот, тогаш I xy =0 и, според тоа, овие оски се главните. Се нарекуваат главните оски што минуваат низ центарот на гравитација на делот главни централни оски на инерција на пресекот
2. Штајнер-Хајгенсова теорема за паралелно преведување на оските
Теорема Штајнер-Хајгенс (Штајнерова теорема).
Аксијалниот момент на инерција на делот I во однос на произволна фиксна оска x е еднаков на збирот на аксијалниот момент на инерција на овој дел I со релативната оска x * паралелна со него, минувајќи низ центарот на масата на пресекот, а производот на плоштината на пресекот A со квадратот на растојанието d помеѓу двете оски.
![]()

Ако моментите на инерција I x и I y во однос на оските x и y се познати, тогаш во однос на оските ν и u ротирани со агол α, аксијалните и центрифугалните моменти на инерција се пресметуваат со помош на формулите:

Од горенаведените формули е јасно дека
![]()
Оние. збирот на аксијалните моменти на инерција кога ротирачките меѓусебно нормални оски не се менуваат, т.е. оските u и v, во однос на кои центрифугалниот момент на инерција на пресекот е нула, а аксијалните моменти на инерција I u и I v имаат екстремни вредностите max или min се нарекуваат главни оски на делот. Се нарекуваат главните оски што минуваат низ центарот на гравитација на делот главните централни оски на делницата. За симетрични пресеци, нивните оски на симетрија се секогаш главните централни оски. Позицијата на главните оски на делот во однос на другите оски се одредува со помош на врската:

каде α 0 е аголот со кој оските x и y мора да се ротираат така што тие да станат главни (позитивен агол обично се поставува спротивно од стрелките на часовникот, негативниот агол се поставува во насока на стрелките на часовникот). Се нарекуваат аксијални моменти на инерција околу главните оски главни моменти на инерција:
Знакот плус пред вториот член се однесува на максималниот момент на инерција, знакот минус на минимум.
Аксијалниот (или екваторијалниот) момент на инерција на пресекот во однос на оската е збирот на производите на бесконечно мали области () преземени на целата површина S, помножени со квадратите на растојанијата од нив до оската на ротација:
Поларниот момент на инерција на пресекот е идентификуван во однос на одредена точка (пол). Поларниот момент на инерција на делот е збир од производите на бесконечно мали области (), преземени над неговата површина S, помножени со растојанието од овие области до полот, земени на квадрат:
![]()
Каде ![]() Во случај на перпендикуларни оски за кои се познати моментите на инерција, поларниот момент на инерција во однос на пресечната точка на овие оски лесно се наоѓа како резултат на собирање на аксијалните моменти на инерција:
Во случај на перпендикуларни оски за кои се познати моментите на инерција, поларниот момент на инерција во однос на пресечната точка на овие оски лесно се наоѓа како резултат на собирање на аксијалните моменти на инерција:
Понекогаш се разгледува центрифугалниот момент на инерција на пресекот, кој се наоѓа како
![]()
изразот (4) вели дека центрифугалниот момент на инерција на пресекот во однос на меѓусебните нормални оски е збирот на производите на елементарните области () според растојанијата од нив до оските што се разгледуваат, на целата површина S.
Аксијалните и поларните моменти на инерција се секогаш позитивни. Центрифугалните моменти на инерција на пресеците може да бидат поголеми или помали од нула. Центрифугалниот момент на инерција на пресекот во однос на оските, од кои едната или двете се совпаѓаат со неговите оски на симетрија, е еднаков на нула.
Аксијалниот момент на инерција на сложен пресек во однос на оската е еднаков на збирот на аксијалните моменти на инерција на деловите од овој дел во однос на истата оска. Центрифугалниот момент на инерција на сложен пресек во однос на две оски нормални една на друга може да се најде како збир на центрифугалните моменти на инерција на деловите во однос на истите оски. Поларниот момент на инерција го има истото својство. Сепак, невозможно е да се додадат моментите на инерција што се наоѓаат во однос на различни оски и точки.
Примери за решавање проблеми
ПРИМЕР 1
| Вежбајте | Одреди го аксијалниот момент на инерција на рамнокрак триаголен пресек околу оската што минува низ неговата основа (сл. 1). Должината на основата на триаголникот е , неговата висина е . |
| Решение | Ајде да направиме цртеж. Дозволете ни да избереме правоаголна елементарна област на триаголен пресек (види слика 1). Се наоѓа на растојание од оската на ротација, должината на едната страна е , другата страна е . Од слика 1 следува дека:
Потоа ја наоѓаме областа на доделената локација како: Моментот на инерција на триаголен пресек во однос на оската Z по дефиниција е еднаков на: |
| Одговори |
ПРИМЕР 2
| Вежбајте | Најдете го поларниот момент на инерција на делот во форма на круг во однос на неговиот центар. Радиусот на кругот е . |
| Решение | Прво, да го најдеме аксијалниот момент на инерција на кругот во однос на оската OZ (види слика 2). Дозволете ни да избереме елементарна област на кругот во форма на правоаголник со страни и . Од Сл. 2 следи |